一种矿井轨道运行小车的振动分析与隔振设计
刘家诚,李川,刘力萌,马晶莹,刘佳潞
(1.河北科技工程职业技术大学,河北邢台,054035;2.河北省特种车辆改装技术创新中心,河北邢台,054000;3.北京航空航天大学,北京,102206)
0 前言
本文研究的矿井轨道运行小车是一种矿井轨道几何状态检测小车(后简称为小车),此小车在机车的牵引下自动地检测矿井轨道的几何状态,即对矿井轨道的轨距、轨向、高低、水平、扭曲等轨道不平顺指标的检测,如图1 所示。检测所用传感器安装于车架上,包含在图1 的检测体总成内,因而车轮与车架之间不能安装减震,否则车架的跳动会影响传感器的精确度。但车架之上的车体里安装的电器设备和供电动力电池都要严格控制其振动[1],因而减震只能安装于车架与车体之间。

图1 小车整体结构图
车体与车架之间隔振设计必须计算减震的刚度,此刚度的分析可采用建立多自由度动力方程组的方法[2],这种多自由度建立方程组的方法研究较为成熟,而且效果良好。本文在满足工程技术要求的前提,建立两自由度方程组,依据小车的运行特性以及振动传递比的要求计算减震的最大刚度,从而完成车架与车体之间隔振设计。
1 小车振动模型与动力学方程
基于小车结构特征,建立图2 所示简化的力学振动模型。车体部分质量为m1,车架质量为m2,车体与车架之间减震刚度为K1、阻尼系数为C1,车架刚度K2,钢质车架结构阻尼较小,可以不考虑。小车垂向激励来自两方面,其一矿井轨道的不平,其二小车车轮的不圆度。这两方面对小车的激励函数均可设为一正弦函数。此处的L 可以是轨道振动周期,也可以是车轮不圆度振动周期对应的长度。即小车沿X 正方向水平行驶,小车将沿铅垂方向振动。设小车行驶的速度为V,在t 时刻,小车车轮(力学模型K2下端)垂向位移为。在t 时刻,应用牛顿第二定律对小车系统写出振动微分方程:

图2 小车两自由度振动模型
将上述方程整理得:
据上述微分方程的特点,方程稳态响应解的形式可表示:
将上式和y=Asintω代入(1)和(2)解得:
本文的目的是设计车体的隔振问题,只需考虑A1 与轨道的激励的关系即可。从(3)式来看,要想知道A1 至少要考虑K2、Y、ω 等参数的情况。
2 车架刚度K2
小车车架结构如图3 所示,它不是一个简单的梁结构,因而很难用材料力学计算梁的弯曲刚度的方法解析,本文只能采用有限元法。小车在运行过程中只考虑铅垂方向的振动,应用有限元计算车架刚度时,小车边界条件和加载方法可参考简支梁的方法求解,如图4 所示。在两前轮转轴位置,做三方向的位移约束;在两后轮转轴位置,约束车宽和车高两个方向,释放车身方向位移约束;在车身两纵梁的中部分别加1000N 的铅垂向下载荷F,车架向下变形有限元法所解如图5 所示。由于本文的有限元分析重点在小车刚度的计算方法的讲解,所以此处省略了车架材料、车架结构一些特征的叙述。
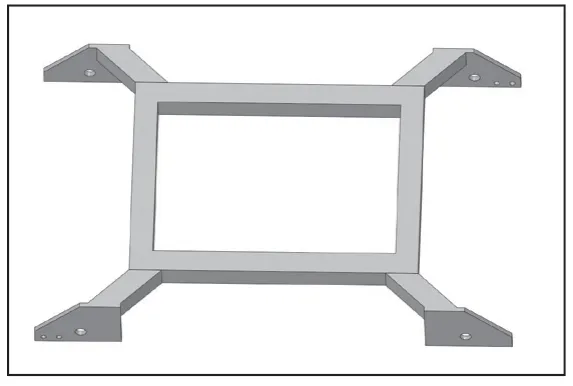
图3 小车车架

图4 小车车架铅垂刚度计算原理图

图5 小车铅垂变形有限元分析云图
从图5 所得,小车车架做有限元解,小车两纵梁中部变形δ 最大约为0.2mm,因而小车在铅垂方向的刚度K2(此刚度不是弯曲刚度)可用下式近似计算[3]:
通过计算得:K2=10000N/mm
3 小车车体振动位移分析
小车在轨道上运行,来自轨道上的激励主要从两方面考虑。其一,我国矿井轨道铺设质量标准为10 米弦长高度差不超过15mm,车速最高限速30km/h,因而取极端情况,小车来自轨道的激励函数可表示为:
其二,小车车轮制造或安装总会存在一些缺陷。在矿井车辆最高限速30km/h 下,矿井机车一般以20km/h 运行,另外,本文小车也可能出现车轮偏心安装、车轮椭圆变形或车轮出现三阶不圆等问题,一般车轮三阶以下不圆居多[4]。为了设计车体隔振,取车轮三阶不圆,因而小车来自车轮的激励可用如下函数表示,其中车轮直径为0.16m。
从(5)、(6)式分析,小车在运行过程中,轨道的曲率对小车的激励频率低而且振幅较小,而来自车轮缺陷的激励频率较高是设计中必须考虑的要素。另外,本小车车体重大约30kg,车架重大约15kg,ω 车轮激励频率208rad/s,通过计算分析车架刚度K2远大于,因而(3)式可忽略小量,并将K2提出来,车体振幅进一步化简为:
4 小车车身隔振的设计
小车在设计过程中,小车需要配置相应的电器设备,电器设备的供电来自车载动力电池,将此电池安置于车体中。在车体运行过程中,车上主体部分多数系统抗震性能比较高,只有动力电池抗振能力低,因而本文按动力电池的抗震要求给小车配置相应的减震机构。按照国际标准,车载动力电池的受振分析,受到的激励小于5 赫兹可以不予考虑[1]。从上文分析中,小车来自轨道平面激振频率较低可以不考虑,小车受到的激励主要来自车轮的不圆度,据上文可知此小车受到的最高激励频率可由下式计算。
从上式可知,小车在轨道上运行,在通常车速下受到轨道激励频率约有33Hz 超出了电池最低考虑激振频率。因而小车运行必须考虑车体的隔振设计,车体隔振设计要求激励与车体振幅的振动传递比如下式所述。
上式中m1约30kg、ω 取208rad/s,可得K1需小于609352N/m。本文研究的小车车架与车体之间安装四个减震,因而每个减震的刚度Kp 小于609352/4=152338 N/m。此刚度较小不适合橡胶弹簧,因此选用刚度范围较宽的圆柱弹簧。
减震弹簧设计如下[5]:
(1)弹簧材料选择及力学参数
选用60SiMnA 弹簧钢,其抗拉强度σb=1568Mpa,剪切模量G=7.8×104 MPa
(2)依据弹簧强度条件确定簧丝直径
初选簧丝直径d=2.5mm。
弹簧旋绕比一般取c=5~8,它是弹簧中径D 与簧丝直径d 的比值,选7。
弹簧许用剪切应力[τ]=0.3σb=470 MPa
簧丝剪切应力计算(下式F 为四分之一的车体重力)
从上式看,簧丝直径初选2.5mm 满足材料强度要求。
(3)依据弹簧钢度条件确定弹簧圈数n
圆整之后n=5 圈
(4)弹簧自由长度H 的确定
一般圆柱弹簧正常使用的压缩量不应超过弹簧自由长度的30%,此弹簧载荷相对稳定,使用时取自由长度的20%,因而弹簧有效自由长度H0为:
又因弹簧两端各需加一支承圈,所以弹簧的总自由长度H=H0+2d=29.5mm。
最终小车车体与车架之间减震设计如图6 所示。

图6 小车减震剖视图
5 结论
本文讲述了一种矿井轨道几何状态检测小车振动位移计算与隔振设计。
由于小车搭载了一些电器设备和动力电池,按照行业设计要求,对小车搭载的这些设备必须进行隔振设计。于是本文根据小车运行工况建立两自由度的振动模型,涉及小车车体的振动和小车车架的振动。小车运行速度较低,轨道弧曲较小,因而轨道的不平对小车的激励可以不考虑。但小车车轮较小,另外车轮在制造和安装过程中会有一定的缺陷,这些缺陷是小车受激的主要来源。车轮的不圆主要集中在三阶以下的不圆,本文为设计小车隔振,小车振动方程的激励采用车轮的三阶不圆对此模型进行求解。在求解过程中,发现车架的刚度远大于隔振采用弹簧的刚度,因而在确立激励与车体之间的振动传动比关系式,省略了一些小量,使两自由度中车体振动解得到简化,方便分析车体隔振采用弹簧的刚度。另外,小车车架不是简单的梁结构,因而在求车架铅垂刚度时,本文采用了应用较广泛的有限元法进行分析计算。一旦分析出隔振弹簧的刚度,就可以对其进行设计。本文设计的小车重量较小,隔振用的弹簧刚度也较小,因而选择了应用较广泛的圆柱弹簧。同时,设计的减震器结构较小,阻尼元件选择了阻尼橡胶垫片吸收车体振动能量。
本文的这种设计方法,可以广泛的应用具有相近结构的各种需要设计隔振的领域。

