认知车联网中基于改进的强化学习的频谱接入方法
陈玲玲,赵全军
(吉林化工学院 信息与控制工程学院,吉林吉林,132022)
0 引言
近些年,伴随着通信技术的高速发展以及物联网与智能汽车的普及,交通行业也逐渐走向了智能化,车联网技术成为物联网与智能汽车两大领域的重要交集[1~3]。因此车联网在智能交通系统中扮演着重要角色。随着通信需求爆发式增长,充分利用频谱资源成为车联网通信的一项重要挑战。
为了提高频谱利用率[4],认知无线电能够通过对空闲频段的智能使用这种方式恰好可以满足车联网通信的需求。于是,认知车联网的概念从此被提出[5-6],即能够支持认知无线电技术的车联网。认知车联网是指通过车载传感器、认知无线电等技术,使车辆之间、车辆与基础设施之间建立起智能化交互,实现信息共享和协同决策,提高交通安全性、舒适性和效率的新型交通系统。认知车联网能通过感知、分析和推理来获取对车辆及其周围环境的认知能力,并通过车辆间和车路间通信来实现协同决策和共同优化的车辆互联网简单来说,就是将车辆、道路和智能化设备进行互联互通,形成一个智能化的交通网络,通过共享和交换数据,实现车辆和交通基础设施之间的智能互动和协同决策,从而提升整个交通系统的效率、安全性和舒适性。在认知车联网中,车辆类型主要分为两种:授权车辆与认知车辆[7-8]。授权车辆优先使用授权频段进行数据传输,认知车辆感知信道状态尝试使用未被授权车辆占有的频段,于是动态频谱接入是认知车联网中的重要难题之一。近些年来,强化学习[9~12]逐渐用来解决动态频谱接入问题。
本文提出了基于新型强化学习的认知车联网频谱接入的方法,构建了存在多个认知车辆,同时包含V2V 与V2I两种不同通信链路的认知车联网环境。通过对比贪婪算法和传统的强化学习方法,所提方法能够有效提高认知车辆接入信道的成功率,本文同时探索了认知车辆数目所提方法的影响,进一步说明所提方法的稳定性。
1 认知车联网通信系统模型
本文建立一个存在V2V 链路与V2I 链路的认知车联网通信模型,为了保证可靠的通信环境,假设每辆车都配备了一个发射机与一个接收机,并且每一条信道仅被一辆授权车辆占用。正如图1 所示,本文考虑的认知车联网场景中包含C辆授权车辆与V辆认知车辆两种类型。授权车辆优先使用授权频段进行数据传输,例如应急救护车与移动演播室车等。为了防止授权车辆之间产生干扰,每一条信道仅被一辆授权车辆占用。如果信道被授权车辆占用,认知车辆应该被限制接入信道,如果当授权车辆没有占有信道时,认知车辆可以接入信道用于通信。在实际的认知车联网中,在认知车辆接入信道之前,认知车辆需要对信道进行感知。
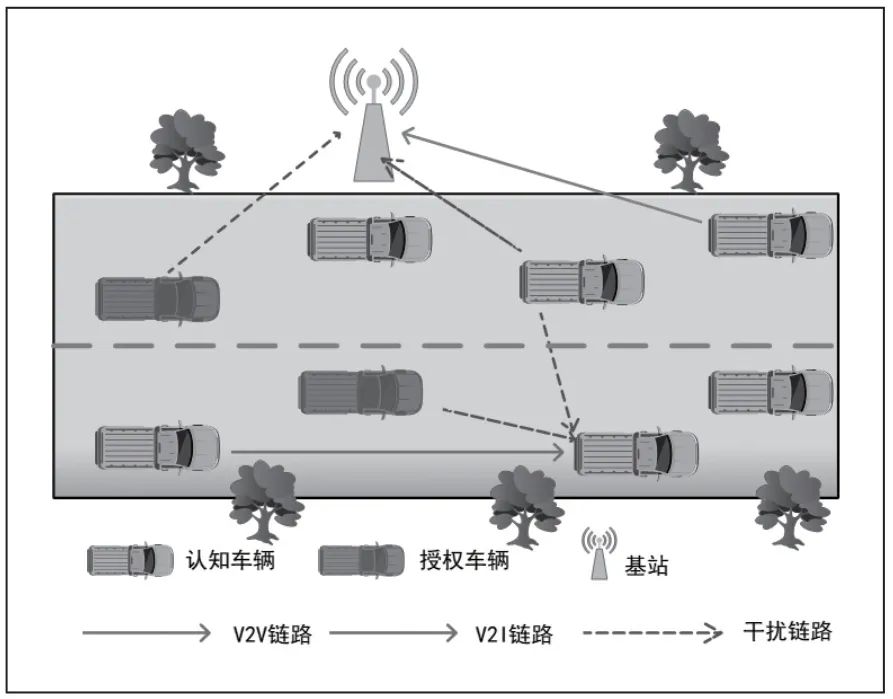
图1 认知车联网通信模型
在基站的通信覆盖范围内,所有的车辆以随机分布的形式存在。因此,本文将所有的车辆映射在一个位于第一象限的二维空间中,其中X轴的范围为[0,M],Y轴的范围[0,N]。,(xBS,yBS),分别代表第i对认知车辆的发射机T的位置,第i对认知车辆的接收机R的位置,第j对授权车辆的发射机T的位置和第j对授权车辆的接收机R的位置以及基站的位置。其中i={1,…,V},j={1,…,C}。
由于本文所设计的反馈函数是与信干噪比(Signal-to-Interference-Plus-Noise Ratio,SINR)有所关联,所以我们需要计算V2V 链路与V2I 链路的SINR。在V2V 链路中的信干噪比SINRV2V公式为:
在V2I 链路中的信干噪比SINRV2I公式为:
2 基于改进强化学习的频谱接入方法
在认知车联网环境中,本文采用强化学习方法解决动态频谱接入问题。本小节针对所研究的认知车辆网中频谱接入的问题设计合理的状态空间,动作空间与反馈函数。
■2.1 状态空间的设计
由于所提出的认知车联网中假设了一条信道中只被一辆授权车辆占用,即正交信道集合为{1,2,…,C}。授权车辆存在两类活动模式,在任意时刻授权车辆都处于两类活动模式中的一类。这两类活动模式分别为:动态(Dynamic)与非动态(Undynamic)。当授权车辆处于动态的时候,意味着授权车辆正在使用信道进行通信,信道处于忙碌状态,认知车辆则限制接入信道;当授权车辆处于非动态的时候,意味着信道处于空闲状态,认知车辆则允许接入信道完成通信。如图2 所示,将授权车辆的活动模式构建为二维的离散时间的马尔科夫链,说明每一条信道都是独立的,互不干扰。一条信道从空闲状态转移到忙碌/空闲状态,或者从忙碌状态转移到忙碌/空闲状态的转移可能性不依赖于其他任何信道。转移概率矩阵如下:
在认知车辆在进行频谱接入之前,每一个认知车辆对每一条信道进行频谱感知,去感知信道处于空闲状态还是忙碌状态,感知结果矩阵设计为状态空间。其中,v={1,…,V},c={1,…,C},=0表示t时刻第v个认知车辆感知到第c条信道被占用,=1表示t时刻第v个认知车辆感知到第c条信道未被占用。
■2.2 动作空间的设计
认知车辆的感知结果决定认知车辆是否接入信道,构成了动作空间:
其中av(t)=c(c>0),表示第v辆认知车辆选择接入第c条信道进行数据传输,av(t)=0表示第v辆认知车辆不接入任何的信道。
■2.3 反馈函数的设计
在传统的基于强化学习的认知车联网频谱接入中,反馈函数r(t+)1 的设计如下:
其中β为一个常数。
传统的反馈函数设计过于简单,并没有考虑到真实的现实情况的复杂性。在V2V 与V2I 链路中,根据认知车辆不同接入情况下的信干噪比,本文重新设计反馈函数rv(t+1),公式如下:
其中B为信道带宽,SINR∈{SINRV2I,SINRV2V}。
本文的目的是利用强化学习方法获取最大的累积反馈Rv,进而提高接入认知车辆成功率,公式如下:
其中γ∈[0,1]为折扣因子,T为时间。
■2.4 算法流程
所提算法目的在满足获取最大的累积反馈Rv,其表示如下:
图3 展示基于强化学习的频谱接入的学习过程,通过不断的学习进而学习到一个策略使累积反馈Rv达到最大。
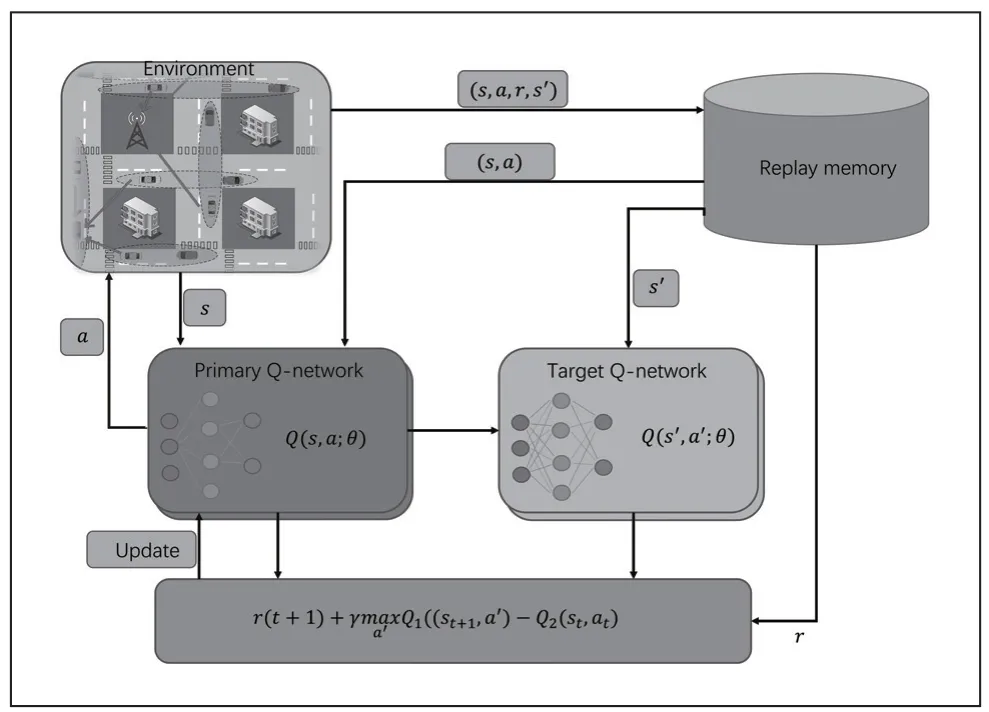
图3 强化学习交互环境
首先认知车辆在获得某个信道的感知结果s时,通过主要网络(Primary Q-network)可以得到各个动作的Q值,Q值用来评估认知车辆接入策略的好坏程度。然后认知车辆再利用贪婪策略进行动作选择,将相应的动作a输入到车联网环境中,最后得到s′和r,这样就得到一个经验(s,a,r,s′)并将其存储到经验池当中。训练时从经验池中取出一定数量的数据进行神经网络的优化。由图3 可知首先根据两个结构相同的主要网络和目标网络(Target Q-network)进行损失函数的构建,在整个过程中通过实现损失函数最小化进而寻找到最优策略,损失函数L(θ)如下:
其中,θ为网络参数。为目标Q网络,Q(s,a;θ)为当前Q网络,s′表示下一时刻的认知车辆的频谱感知结果,a′表示下一时刻的认知车辆的动作。目标Q网络与当前Q网络的网络完全相同。在训练过程中,Q值根据公式(10)不断更新。在Q值不断更新的过程中,动作a′根据公式(11)进行策略π的更新,具体公式如下:
其中,Q1(·) 表示目标Q网络的Q函数,Q2(·)表示当前Q网络的Q函数,表示更新后的Q值,表示原始的Q值,智能体会周期性在经验池中随机地选择样本进行训练。其中ε的范围为 ε∈[0,1),网络参数不断迭代更新,最终逐渐收敛到最优策略。
3 实验与结果
本文采用贪婪算法,强化学习算法作为对比算法,通过试验仿真来验证所提方法在收敛速度与性能远远优于其他对比方法。同时实验还探讨了认知车辆数目对所提方法的影响。
如图4 所示,认知车联网存在5 个认知车辆,10 条信道。为了公平对比,所提方法与其他对比的方法都设置了相同的模型参数。如图4 中所示,总体而言,所提方法的性能与收敛速度明显优于其他方法。对于贪婪算法而言,其平均信道成功接入率基本不变,这是由于贪婪算法无法利用未来的信息,导致无法得到最优的累积奖励。然而传统的强化学习算法的反馈函数设计得过于简单,并不能有效地减少各类碰撞。训练开始,所提方法的信道接入率比其他对比方法都高。总体而言,在认知车辆的接入信道的平均成功接入率,所提出方法的收敛性与性能明显优于对比算法。
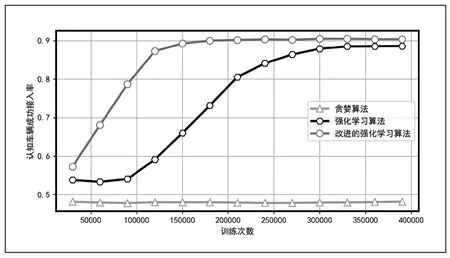
图4 平均成功接入率
为了探究所提方法的稳定性,如图5 通过构建相同信道数目,不同认知车辆的数目的认知车联网环境,用来探究认知车辆数目对所提方法的影响。伴随着训练次数的不断增加,三种不同认知车联网环境下的认知车辆的平均信道成功接入率都开始趋向收敛。由于所提方法考虑到了多种反馈以及竞争网络能够处理大尺度的动作集合与状态集合,最终,三种不同认知车联网环境下的认知车辆的信道接入率都达到了90%左右。
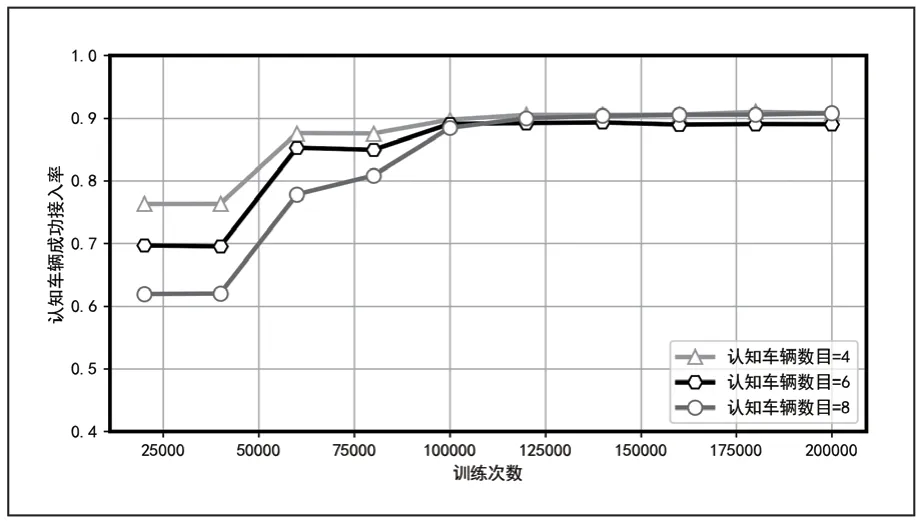
图5 平均成功接入率
如图6 所示,在认知车辆的平均累积反馈方面,所提方法的平均反馈值明显优于对比算法,这是由于所提方法考虑到了认知车辆在当下状态中每一个动作的重要性。从图6中可以看出,所提方法的收敛性和性能明显优于传统的强化学习算法和贪婪算法的收敛性和性能。

图6 平均累积反馈
4 结语
在本文中,所提方法考虑了一个包含V2V 与V2I 链路认知车联网通信环境,建立以提高认知车辆接入信道成功率的动态频谱接入问题的模型。为了提高接入信道成功率,本文将认知车辆的频谱感知结果与认知车辆是否接入信道分别作为所提方法中的状态空间与动作空间。根据认知车辆的信干噪比设计反馈函数,本文提出了改进的强化学习方法用来提高认知车辆的频谱接入率。通过对比传统的强化学习算法与贪婪算法,本文所提出的改进的强化学习方法性能优于其他对比算法。同时还探讨了认知车辆数目对所提方法的影响,通过仿真实验证明,所提方法并不受认知车辆数目的影响,所提的方法具有显著的稳定性与收敛性。

