隧洞围岩蠕变模型的试验研究
吴祖德
(崇义县水利局,江西 崇义 341300)
0 引 言
隧洞工程是水利、交通、能源等领域的重要基础设施,其安全性和稳定性直接关系到工程效益和社会效益。隧洞围岩作为隧洞结构的主要承载体,在地应力、水压力、温度等因素的长期作用下,会发生持续的时间依赖性变形,即蠕变现象。蠕变会导致围岩强度下降、裂缝扩展、支护结构受力增大等不利后果,对隧洞工程的设计、施工和运营造成严重影响。因此,深入研究隧洞围岩的蠕变特性及其对隧洞结构安全性的影响,对于优化支护方案、控制变形损坏范围、提高运营寿命等具有重要意义。
目前,许多学者开展了大量关于隧洞围岩蠕变模型的试验研究,并提出多种描述围岩蠕变行为的理论模型。徐鹏等[1]通过三轴循环加卸载蠕变试验,建立并验证岩石的黏弹塑性和弹塑性损伤两种蠕变模型,同时引入损伤因素,建立弹塑性损伤蠕变模型,分析了岩石的蠕变应变、速率和损伤特性。张明珠等[2]采用MTS815.02岩石试验系统,进行不同温度作用下的三轴蠕变试验,并建立了一种新型岩石温度-围压耦合的时效性蠕变模型,结果表明该模型能很好地描述岩石的蠕变变形特性及加速蠕变阶段的变形特性,并验证了温度、围压和时间对岩石蠕变特性的影响。林韩祥等[3]通过室内三轴蠕变试验和模型辨识技术,建立非线性黏弹塑性蠕变模型,将其在常规三轴应力状态下的蠕变方程编程,并嵌入非线性拟合模块,拟合结果与试验结果吻合,揭示了滇中引水大埋深隧洞围岩的非线性蠕变力学特性。李祥春等[4]进行低瓦斯压力下的分级加载轴压时型煤蠕变实验发现,经验函数和Burgers模型等存在缺陷,经过优化的西原加速模型具有可靠性,并提出蠕变拐点的观点,可为预防岩石失稳破坏等工程实践提供借鉴。曹文贵等[5]基于岩石蠕变的阶段性特征和损伤理论,构建出反映岩石非线性蠕变特征的弹塑性损伤体元件模型,并与Kelvin元件模型串联复合,提出简单可行的模型参数确定方法,建立了岩石蠕变全过程的新型模拟方法。
在已有研究的基础上,本文采用MTS815.02岩石力学试验系统,对某隧洞粒径为10~15mm的泥质粉岩石进行5个应力水平下的压实蠕变试验,建立一种岩石压实蠕变过程中的应力-应变本构关系。
1 试验设计
1.1 设计步骤
本次蠕变试验采用的仪器设备是MTS815.02岩石力学试验系统。岩石样品为质量1 700g、尺寸10~15mm泥质粉岩石,其单轴抗拉强度57.5MPa,密度ρ为2 473kg/m3,含水率为天然含水率,先后对饱和含水率的泥质粉岩石以及天然含水率的泥质粉岩石开展蠕变试验。具体的蠕变试验步骤如下:
第一步:将岩石样品进行饱和处理,在进行轴向加载之前,岩石样品必须进行饱和。将岩石试样装入蠕变试验模具内,采用真空泵抽真空处理8h,然后向真空泵中加入无气水,让试样达到饱和状态。对于天然含水率的泥质粉岩石蠕变试验可以忽略此步骤。
第二步:轴向压力加载,按照25、50、100、200以及400kN的轴压依次进行轴向加载,每级压力的加载时间为40s,当加载到下一级压力时,不卸载原先的压力。每次施加轴向压力后保持稳定,等待岩石样品开始蠕变。每个加载级别及其保持时间见表1。MTS815.02岩石力学系统被设置为每隔5s收集岩石样品的试验数据(包括位移、载荷)。

表1 每级轴压和持续时间
1.2 宏观应变的计算方法
根据试验得到的轴向蠕变位移S,可以采用式(1)计算出试验样品在不同时间t下的堆积高度h和轴向应变ε;通过对ε-t曲线和σ-ε的拟合,可以得到蠕变模型在进行计算时所需要的计算参数。
(1)
式中:ε为应变,m;h为t时刻下的堆积高度,m;h0为试样初始高度,m;S为试样轴向蠕变位移,m。
2 试验结果分析
饱和泥质粉岩石的质量1.7kg,初始堆积高度102mm,试验模具的内径127mm,采用式(2)可以计算其初始堆积密度为1 316kg/m3。
(2)
式中:ρp为初始堆积密度,kg/m3;m为饱和泥质粉岩石质量,kg;D为模具内径,mm。
饱和泥质粉岩石蠕变试样在5种不同轴向荷载作用下的时间-位移曲线见图1。
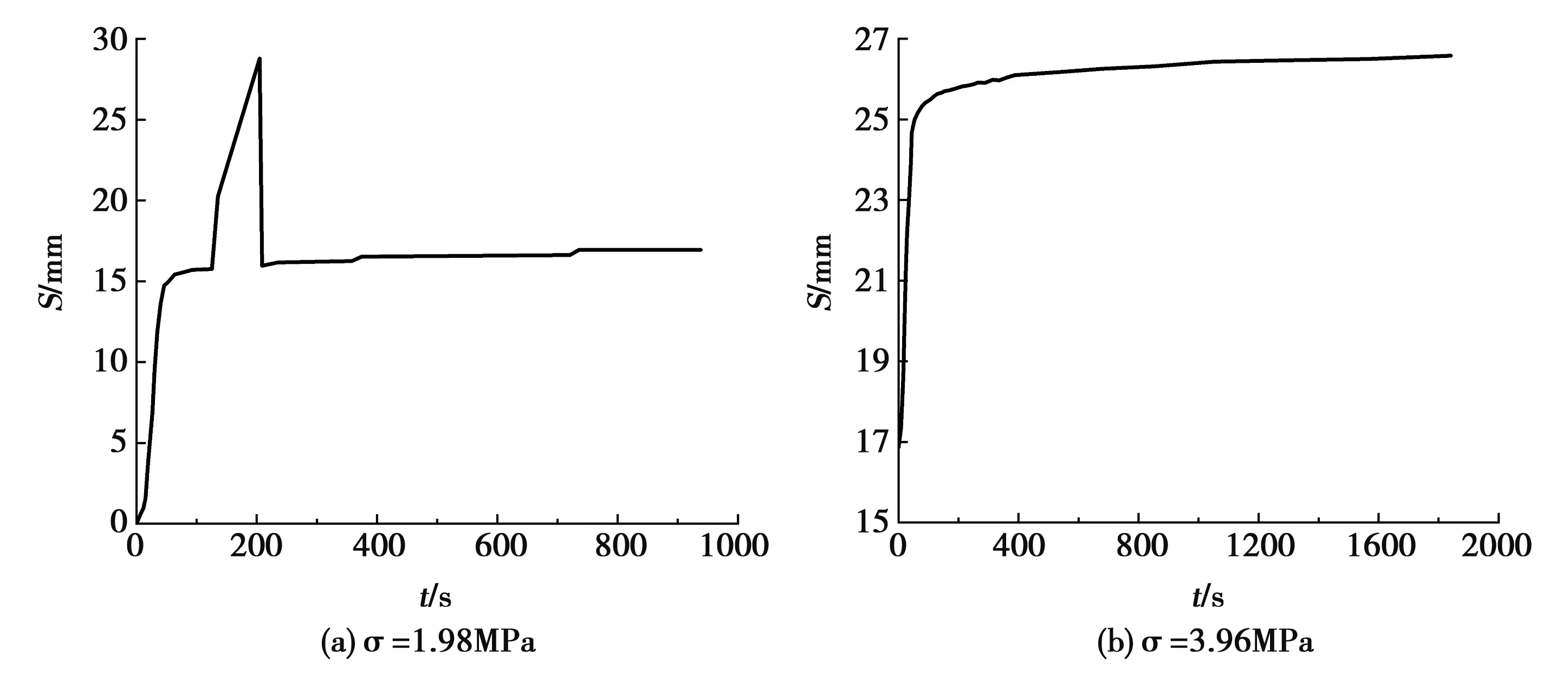
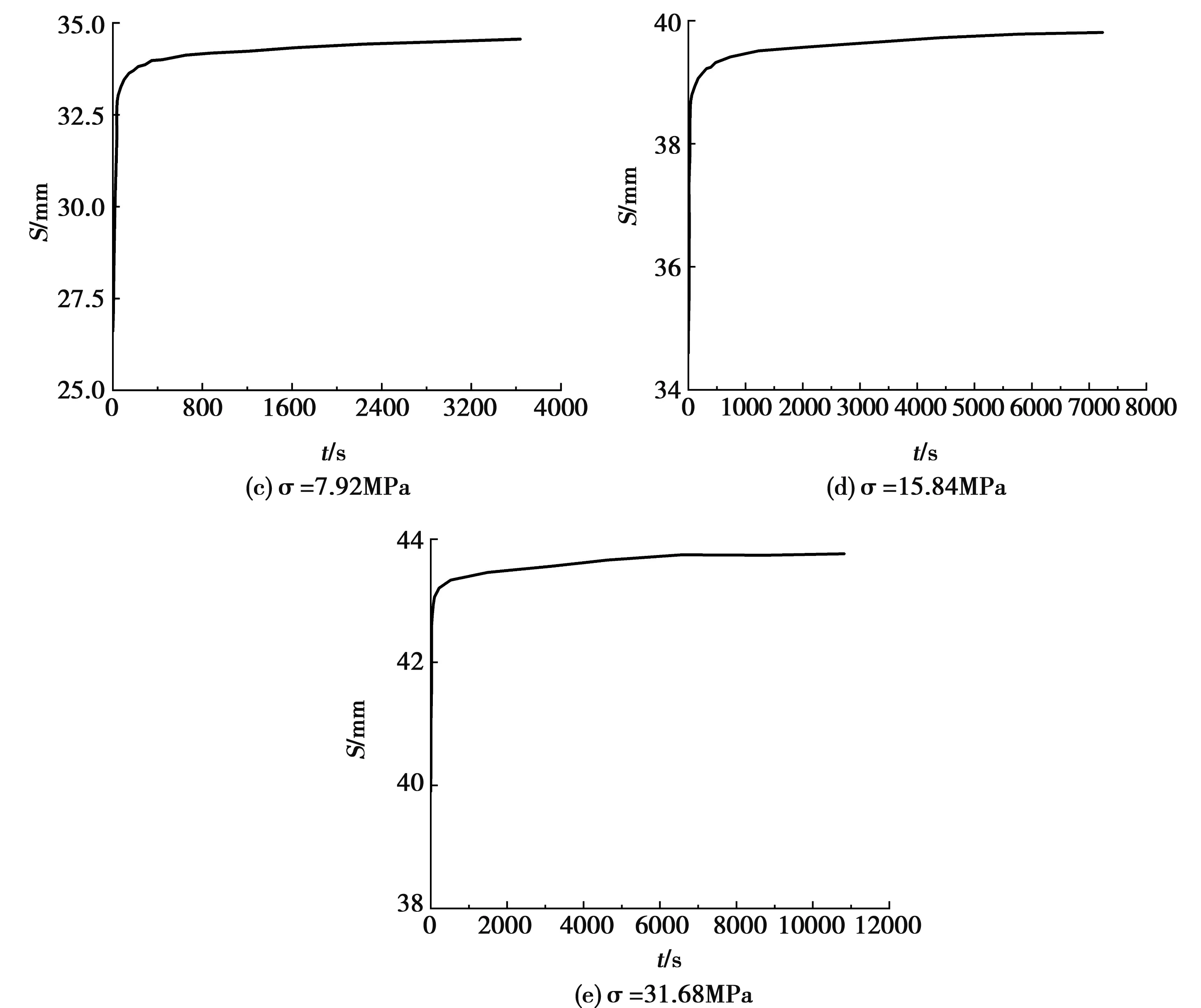
图1 不同轴向荷载下的时间-位移曲线
由图1可知,饱和泥质粉岩石试样在一次蠕变后的变形趋于稳定。从图1(a)可以发现,蠕变曲线在1.98MPa处有明显的波动,这是由于岩石颗粒在轴向压缩力作用下位置突然改变所致。图1中的5种应力水平下的变形均包括加载阶段的瞬态变形和保持阶段的蠕变变形。
3 饱和泥质粉岩石的蠕变模型研究
3.1 常见的蠕变模型
常见的蠕变模型有Maxwell模型、Kelvin模型、Kelvin-Volgt模型(K-V模型)以及Burgers模型等,模型的具体实现方式见图2。
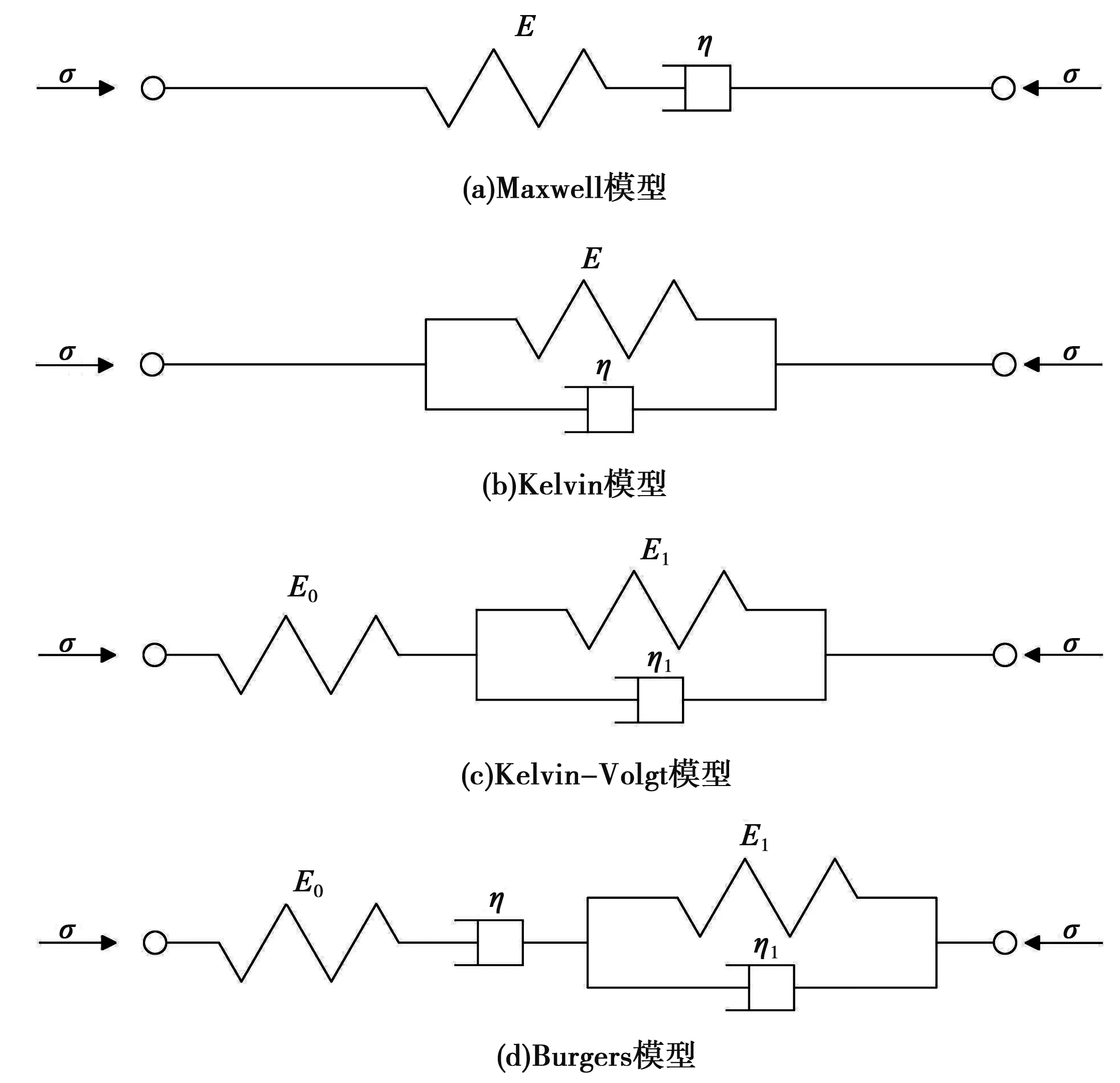
图2 4种常见蠕变模型
在这4种模型中,Maxwell模型和Burgers模型的蠕变大小会随着时间的增加而增加,最终蠕变大小会趋于无穷。因此,Maxwell模型和Burgers模型是液体模型,与泥质粉岩石的实际蠕变情况不一致。所以,在对泥质粉岩石的蠕变试验结果进行分析时,不能使用Maxwell模型和Burgers模型。Kelvin模型不能反映材料的瞬时弹性变形,显然与泥质粉岩石蠕变试验结果中的弹性特性不一致,所以也不能使用。只有Kelvin-Volgt模型能够反映蠕变规律和瞬时弹性特性,因此本文采用Kelvin-Volgt模型(K-V模型)分析泥质粉岩石的蠕变试验结果[6-7]。
K-V模型的本构关系如下:
(3)
式中:E0为瞬时弹性模量,MPa;E1为极限蠕变变形模量,MPa;τ1滞后时间,s。
τ1的计算方法如下:
(4)
式中:η1为黏性系数。
3.2 K-V模型参数计算
瞬时弹性模量E0可以由加载阶段的应力和弹性应变确定。在第一个应力水平σ=1.98MPa时,收集30s内的位移S、轴向力F等数据,见表2。利用表2绘制的应力-应变图进行拟合,可以得到饱和碎砂岩在σ= 1.98MPa时的E0= 13MPa。
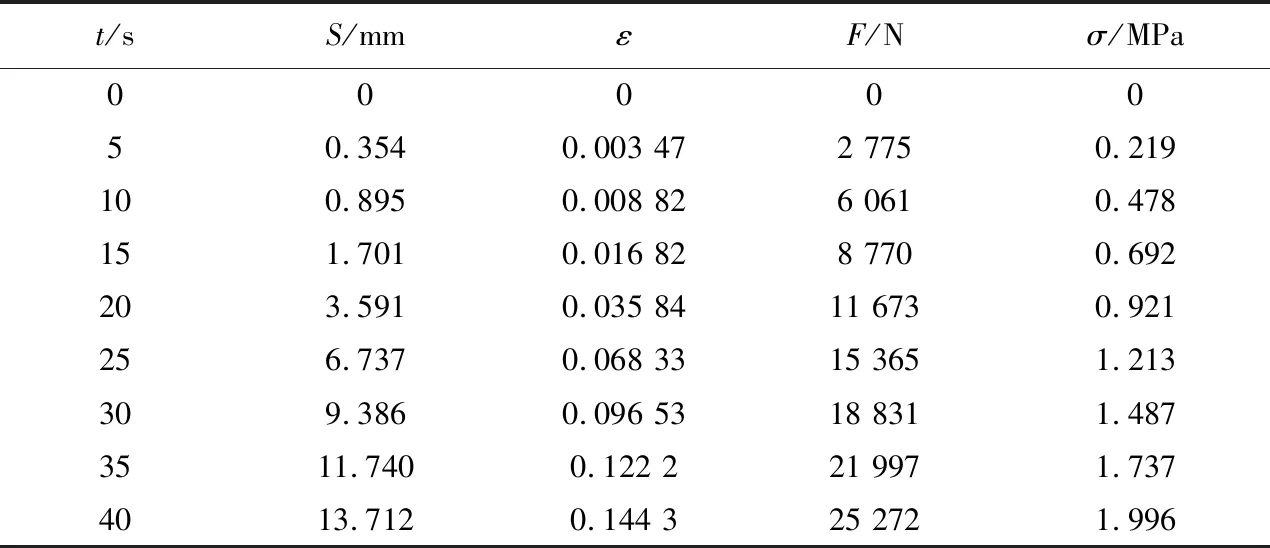
表2 σ=1.98MPa时的应力和应变
对极限蠕变变形模量E1和黏性系数η1进行计算。瞬时弹性应变可以表示为:
(5)
极限蠕变可以表示:
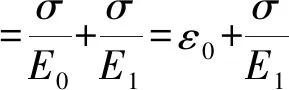
(6)
结合式(5)、式(6)可以得到:
(7)
根据试验数据可知当σ0=1.98MPa时,ε0=0.1443。当试验时长为940s时,ε/ε0=1.247,令ε∞=1.5ε0,通过式(7)计算得到E1=27.35MPa。
将式(3)变形可以得到:
(8)
再对式(8)两边同时积分可以得到:
(9)
令y=ln[σ-E1(ε-ε0)],a=-E1/η1,b=lnσ,式(9)可以简化为:
y=at+b
(10)
通过对试验数据进行拟合可以得到,a=-0.1426,η1=-E1/a=191MPa·s。
通过这种方法,可以得到不同轴压下的泥质粉岩石的蠕变参数,见表3。

表3 饱和样品的蠕变参数
通过对表3数据的处理可以得到,E0= 4.82σ1.1389,E1= 10.05σ1.3029,η1= 73.55σ1.349。
3.3 天然含水率泥质粉岩石的位移-时间曲线
5组不同轴压下的位移-时间曲线(S-t曲线)见图3。
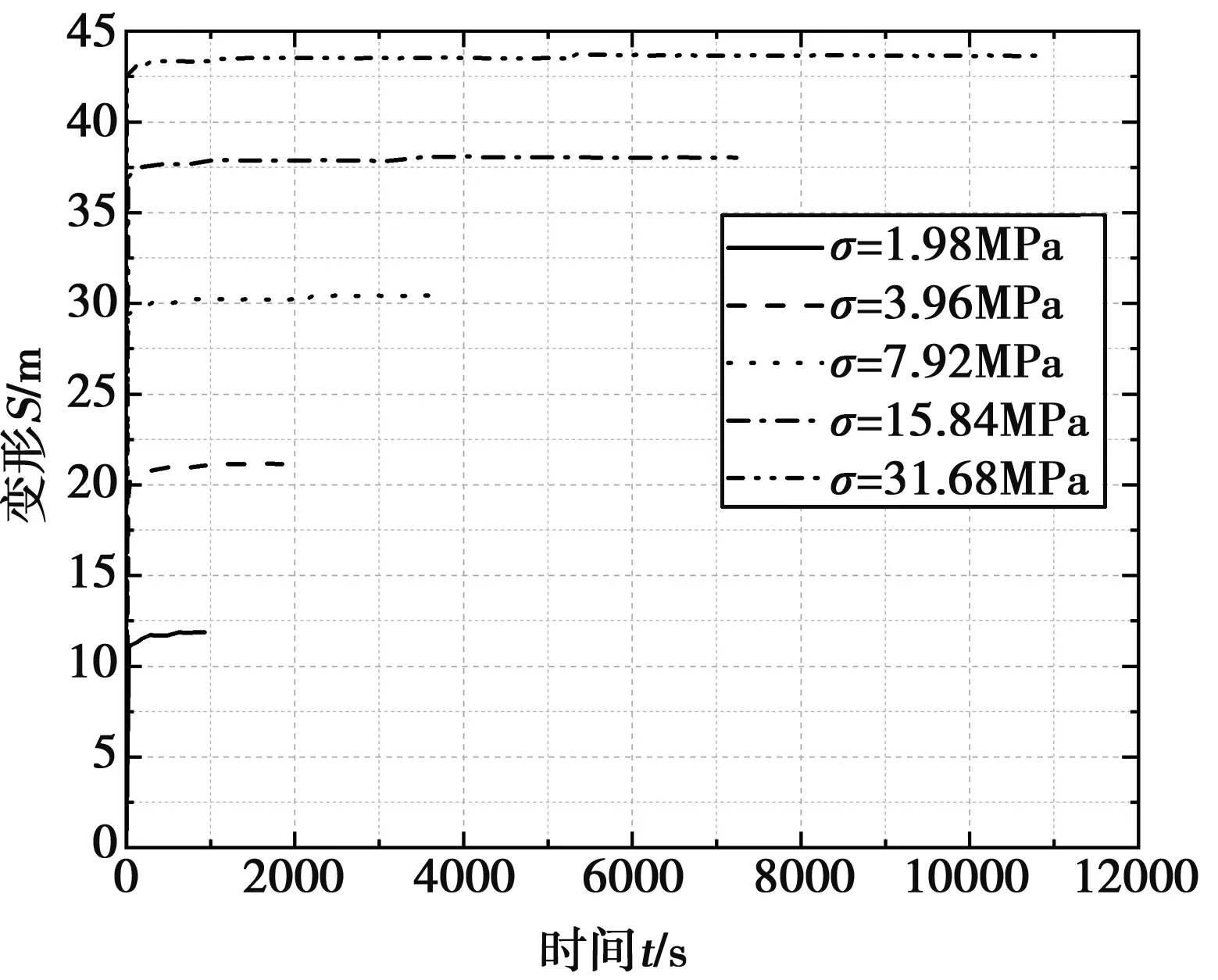
图3 天然含水率试样的S-t曲线
3.4 天然含水量泥质粉岩石的蠕变参数
利用上的计算方法,可以得到天然含水量泥质粉岩石在不同应力水平下的蠕变参数,见表4。

表4 天然含水率样品的蠕变参数
通过对表4数据的处理可以得到,E0=7.62σ0.8797,E1=23.97σ1.197,η1=213.23σ1.0311。将两种不同含水率的E0-σ曲线、E1-σ曲线及η1-σ曲线进行绘制,见图4。
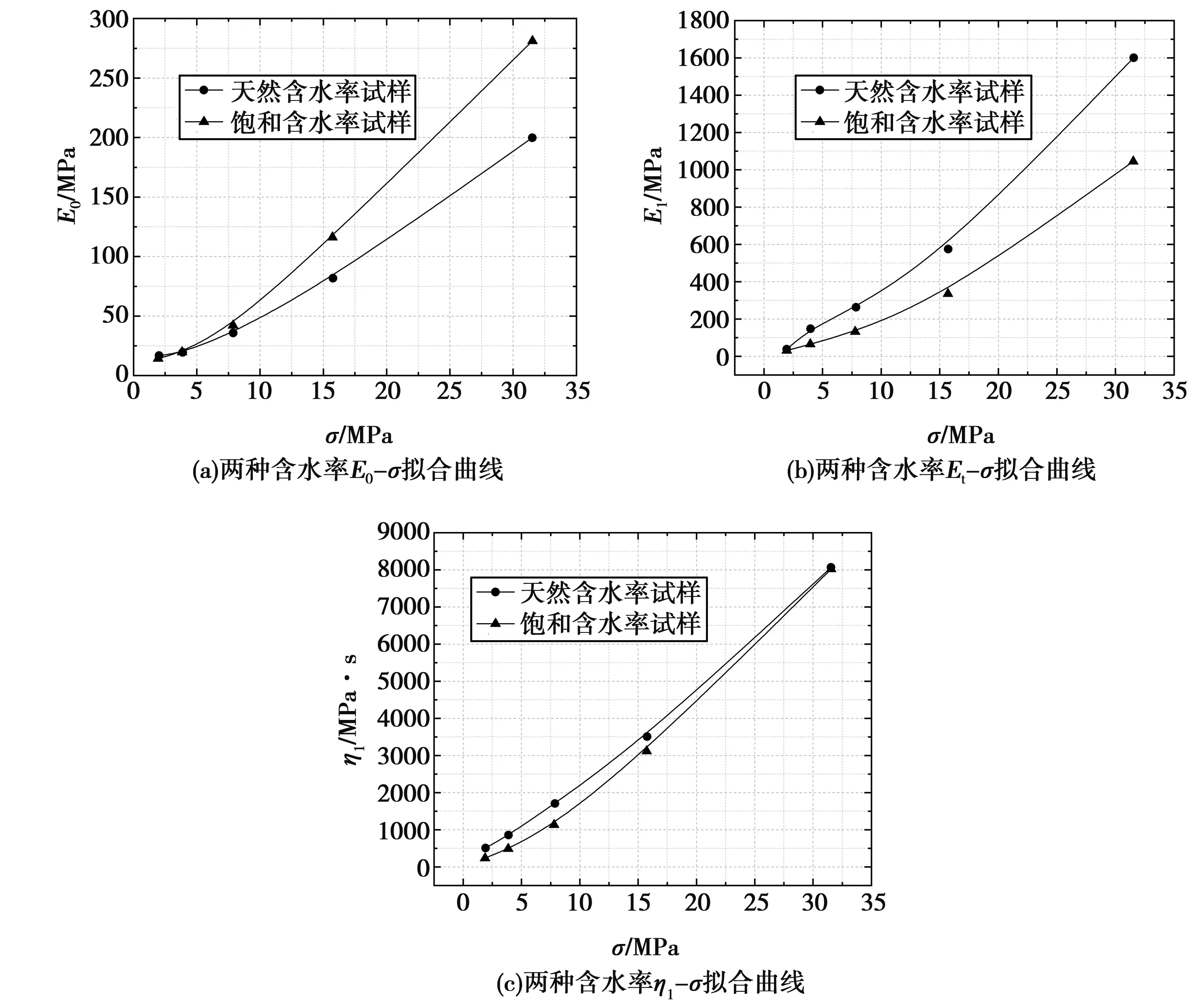
图4 天然含水率与饱和含水率试验结果对比
从图4(a)可以发现,在第一个应力水平下,饱和泥质粉岩石的瞬时弹性模量E0略低于自然含水量的泥质粉岩石,而孔隙水的存在是导致E0降低的主要原因。随着压实的进行,饱和泥质粉岩石试样中的孔隙水被排出,饱和泥质粉岩石试样接近自然含水量的泥质粉岩石。但由于饱和泥质粉岩石的初始堆积密度略大,在初始应力水平下,其压实变形相对较小。因此,从第二个应力水平开始,饱和泥质粉岩石的瞬时弹性模量E0略大于自然含水量的泥质粉岩石。从图4(b)和图4(c)可以发现,随着应力水平的增加,极限蠕变模量E1和黏度系数η1也增加,并且自然含水量的泥质粉岩石的E1略大于饱和泥质粉岩石的E1,但这两个样品的系数η1几乎没有差异。
4 结 论
通过MTS815.02岩石力学试验系统,对饱和泥质粉岩石和自然含水量泥质粉岩石进行了应力水平下的蠕变验,获得了位移-时间曲线和开尔文-沃尔格特蠕变模型参数。结论如下:
1)随着应力水平的增加,两个试样的蠕变参数明显增加。
2)相同的应力水平下,具有较高初始堆积密度的饱和泥质粉岩石具有较大的瞬时弹性模量和较低的极限蠕变模量,但这两个试样的黏度系数几乎没有差异。
3)初始应力水平下,饱和泥质粉岩石的压实变形相对自然含水量的泥质粉岩石较小。因此,从第二个应力水平开始,饱和泥质粉岩石的瞬时弹性模量E0略大于自然含水量的泥质粉岩石。

