爆炸地震动下矩形储液结构动力响应理论研究*
张浩天,宋春明,王明洋,2,赵雪川,吴红晓,郑际镜
(1.陆军工程大学爆炸冲击防灾减灾国家重点实验室,江苏 南京 210007;2.南京理工大学机械工程学院,江苏 南京 210094;3.中国人民解放军96911 部队,北京 100010)
国际安全形势瞬息万变,精确制导系统和新型钻地武器的研发对防护工程设计提出了更高的要求。伴随武器爆炸释放的巨大能量,强烈的冲击地震动传播范围极广,其烈度一旦超过安全容许值,将导致工程结构内部人员受伤和设备仪器受损,严重时将造成整体工程丧失预定的设计功能,乃至影响到全局安危[1-5]。而储液结构(liquid storage structure, LSS)作为一类重要内部设备,其在爆炸地震动下发生破坏,致使易燃易爆、有毒的化学制剂泄露外流,不仅会造成土壤、水资源污染,还可能引发火灾、二次爆炸等重大次生灾害,对人民生命和财产安全形成威胁[6-9]。因此,推进储液结构地震响应理论计算研究,并有针对性地将其用于爆炸冲击震动效应分析,对于防护工程设计具有重要意义。
近年来,学者针对储液结构动力响应计算方法开展了大量研究。Westergaard 等[10]对地震作用下重力坝动水压力进行分析,得到了刚性坝体上液动压力的分布解。Hoskins 等[11]利用简易振动台提供水平地震激励,发表了矩形储液结构地震响应研究报告,并提出利用质量块等效液体作用的思路。延续该思路,Honsner[12-13]提出两质点弹簧-质量计算模型,将地震所致液动压力分为脉冲压力和对流压力,分别等效为与结构刚性连接、弹簧连接的质量体系。由于储液结构在地震中发生破坏时有发生,一些学者对储液结构刚性假设的有效性提出质疑,推动了对柔性储液结构动力响应研究的发展。Veletsos[14-15]假定储液结构按照给定形式发生挠曲变形,提出弹性储液结构简化计算方法,通过对基底剪力和倾覆弯矩进行评估,发现计入结构变形后液动压力有所提高。Haroun[16]建立了圆柱形储液结构流固耦合理论分析模型,提出了将液体作用等效为脉冲质量刚性项、柔性项以及对流质量作用的三质量-弹簧模型,并指出考虑结构壁板弹性会增大地震响应。此类将连续的液体简化为弹簧-质量体系的等效方法便于工程应用,是相关规范中常见的方法。
一些学者将储液结构简化为梁式结构,主要考虑竖直方向液动压力和结构动力响应变化。居荣初等[17]在内流液体微幅晃动的假设前提下,基于流体速度势函数推导了储液结构壁板和底板的液动压力。魏发远等[18]、杜永峰等[19]、程选生等[20]分别基于弯曲、剪切、弯剪型悬臂梁理论建立了储液结构计算模型,对比不同高度和不同变形理论的自振特性,为工程计算提供了依据。Chen 等[21]提出了一种利用悬臂梁广义单自由度方法开展储液结构抗震研究的简化方法,通过案例分析发现该方法适用于储液结构设计。程选生等[22-23]考虑地基、底板和壁板的弹性,研究了矩形储液结构的耦合振动、液动压力以及液体晃动问题。部分学者考虑壁板变形与液动压力具有二维分布特点,即不仅沿竖直方向变化,而且沿水平方向变化。Haroun[24]研究了水平和竖向地震作用下矩形储液结构的壁板荷载评估问题,通过经典势流理论计算得到了弹性壁板的液动压力,给出了力矩的解析表达式及力矩系数。Kim 等[25]研究了矩形储液结构的振动模态和动力响应,假定垂直于地面运动方向的壁板具有柔性特征而另一对呈刚性,建立了固支-自由-对边简支壁板和固支-自由-对边固支壁板两种计算模型,发现随着壁板宽高比增大,结构基频逐渐趋近于悬臂梁模型计算结果。进一步地,Hashemi 等[26]将四面壁板均视作柔性,基于水平-连续梁和竖直-悬臂梁变形理论得到了折板计算模型。
总的来说,储液结构作为生命线工程的重要一环,其安全性能备受关注,已有的研究成果为工程设计提供了支撑。然而,以往通过理论求解储液结构动力响应相对复杂,且大多关注自然地震效应,尚未考虑武器爆炸诱发冲击地震动的影响。因此,有必要提出相关计算与分析方法,为防护工程储液结构设计和评估提供理论依据。本文中研究对象为置于主体结构内部的地面式储液结构,其底板与地面锚固,如图1 所示[8]。假定主体结构在爆炸中未发生严重破坏,故储液结构不受破片、超压等直接作用,而其底板受强烈冲击震动驱动。考虑水平向地震动下壁板分布弹性及其二维特征,简化储液结构为广义单自由度体系,建立运动方程并得到液-固体系动力特性广义参数,求解动力响应并采用振动台模型试验进行验证。利用算例分析储液率、地震动要素对结构动力特性、动力响应的影响规律,进而构建爆炸冲击震动下储液结构动力响应谱,以满足储液结构防护设计简易、快速计算的要求。

图1 作为主体结构内部设备的储液结构[8]Fig.1 Liquid storage structure (LSS) as an internal device in the main structure
1 理论推导
1.1 储液结构运动方程
1.1.1 简化模型
矩形无顶盖储液结构计算模型如图2 所示,地震动沿x方向,定义平行地震作用方向为结构长2Lx,垂直地震作用方向为结构宽2Ly,结构高为Hs,结构密度为ρs,壁板厚度为ds;液位高度为Hl,液体密度为ρl。
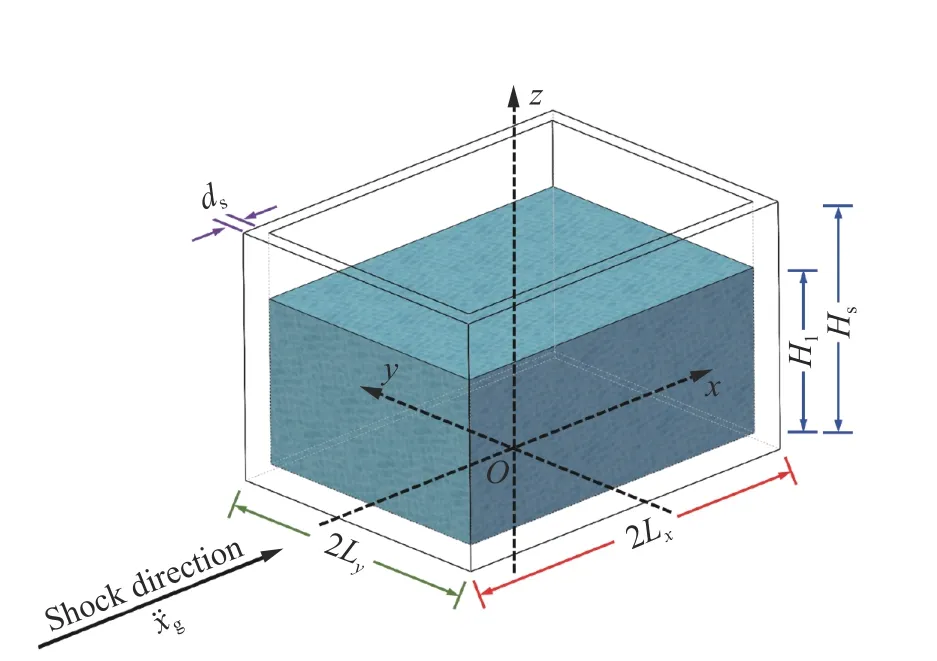
图2 储液结构计算模型Fig.2 Calculation model of the LSS
考虑yz壁板为储液结构受地震惯性力和动水压力作用的主要壁板,按其常见尺寸特征作薄板问题处理。对于匀质材料等截面壁板,其单位面积质量m(y,z)与弯曲刚度D(y,z)分别表示为
式中:E为弹性模量,ν 为泊松比。外部阻尼系数设为c(y,z)。
1.1.2 建立方程
将储液结构作为广义单自由度体系进行分析,该二维体系具有分布弹性,壁板仅产生单一形式的连续弯曲变形,故其挠度xs(y,z,t)可表示为
式中:ψ(y,z)为形状函数;X(t)为广义坐标,即以ψ(y,z)为单位的挠度幅值。采用虚功原理建立储液结构运动方程,即分别计算内力虚功δWI和外力虚功δWE,使二者相等得到方程。
(1) 内力虚功
考虑薄板弯曲变形,故内力虚功δWI主要计算内弯(扭)矩在其对应的虚曲(扭)率上做的功,表示为

式中:p(y,z,t)为基于势流理论得到的作用于弹性壁板的动水压力。鉴于爆炸地震动往往具有高频特征,其主频远高于内储液体的晃动基频,故主要考虑动水压力的脉冲成分而忽略对流的影响[7-9]。假定内储水为无黏性且不可压缩的理想流体,则动水压力表示为[25]
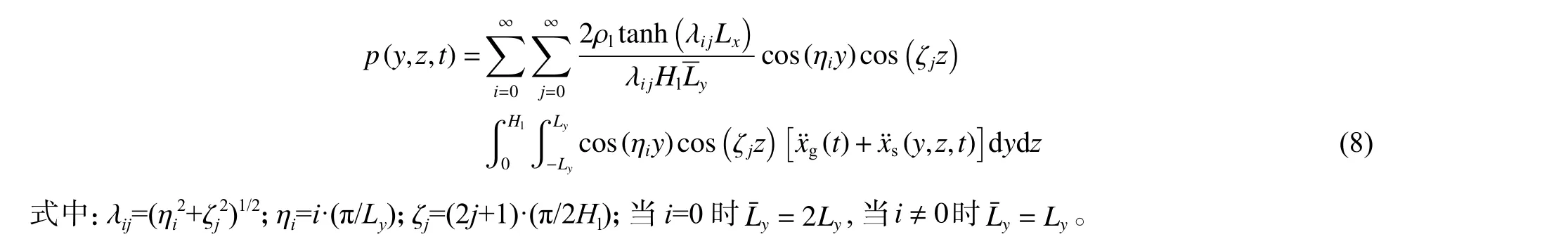
(3) 简化方程
基于虚功原理建立广义单自由度体系运动方程。考虑有δxs(y,z)=ψ(y,z)·δX,并将式(3)代入式(4)~(8),内力虚功和外力虚功可分别改写为

考虑到式(17)等号右侧负号表示等效荷载与地面加速度反向,在地震响应分析中无意义而可忽略,于式(13)等式两侧同除以广义质量m*,将其改写为
式中:ω=(k*/m*)1/2为Rayleigh 法求得的振动圆频率,ξ=c*/(2m*·ω)为阻尼比,F˜ =F*/m*为地震动激励特征因子(简称“特征因子”)。解式(19)得到广义坐标X(t),代入式(3)即可得到结构挠度xs(y,z,t)。
1.1.3 求解方程
将储液结构视为广义单自由度体系,同时作为线弹性体系进行分析。因此,结构时程总响应可由一系列连续冲量产生的微分响应叠加得到,考虑储液结构在初始时刻处于静止状态,故其动力响应广义坐标X(t)可以通过Duhamel 积分得到[27]
式中:ωD=ω·(1-ξ2)1/2为阻尼体系的振动圆频率。特别地,考虑承受冲击荷载时,结构响应在短时间内达到极值,阻尼耗能的影响不大,同时出于防护工程安全设计要求,阻尼可忽略不计[27]。因此,式(20)可简化为
对于正弦波脉冲等简单形式的冲击荷载,可求解得到运动方程的解析解。对于较复杂、具有震荡特征的地震动,需要通过数值方法进行求解。
1.2 储液结构动力响应谱
由于爆炸场地复杂,爆炸冲击震动的准确波形难以预测,通常采用较符合实际的假定波形并进行分析[1]。在选定波形并确定加速度峰值A0和持续时间t0(简称“持时”)后,得到地震动加速度x¨g(t) ,进而可通过式(21)计算储液结构动力响应广义坐标X(t),其最大绝对值记为Xmax,则储液结构挠度最大值xmax表示为
至此,可得到该选定波形下,结构挠度最大值对于地震动加速度峰值和持时的映射关系xmax(A0,t0),构成储液结构挠度响应谱。
若以地震动持时与结构振动周期之比(t0/Tn)为横坐标,以结构最大挠度与单自由度等效静力挠度之比(xmax/xstatic,即xmax/(A0/ω2))为纵坐标,可以得到无量纲的标准化储液结构动力响应谱。对于某一选定的地震动波形,放大或缩小其t0或A0,标准化动力响应谱不随之改变。由此,在储液结构设计时,可通过遍历足够的地震动波形进行计算,得到不同结构选型可能发生的最大动力响应,相较之下确定防护工程储液结构设计更优方案。
2 试验验证
2.1 试验方法
基于爆炸冲击震动模拟平台开展储液结构动力响应模型试验,如图3 所示。通过置于振动台的加速度传感器记录输入地震动信号,粘贴于内壁顶部中心的应变片记录结构应变信号,内壁底部中心的动水压力传感器记录动水压力信号。

图3 试验平台、结构模型与传感器布置Fig.3 Test platform, structural model, and sensor layout
试验模型为矩形无顶盖储液结构,材料为201 不锈钢,内储液体为自然常用水,结构尺寸、材料特性等计算参数见表1。
因现场施工条件限制,托换新桩采用人工挖孔端承桩,桩端入微风化不小于1m,且低于隧道底板不小于2m。南侧地势低,新桩出露地面近20m,为满足桩抗震水平承载力要求,桩端入微风化不小于3m。

表1 储液结构模型计算参数Table 1 Calculation parameters of LSS model
试验时,摆锤下落撞击振动台以提供单次近半正弦加速度脉冲。通过调整摆锤下落高度Hi与缓冲垫块厚度,可以得到不同峰值与脉宽的地震动。在橡胶缓冲垫块厚度为50 mm 时,得到H1~H5(分别为1 140、 1 340、 1 540、 1 740、1940 mm)等5 种摆锤下落高度时的输入加速度信号,如图4 所示。

图4 不同摆锤高度下振动台输入加速度时程曲线Fig.4 Time-history curves of input acceleration of shaking table at different pendulum heights
2.2 理论计算及验证
采用双向梁函数组合法,考虑矩形壁板形状函数ψ(y,z)由横向两端弹性嵌固梁一阶振型Y(y)和竖向剪切型悬臂梁一阶振型Z(z)组合得到[6-8,28],即

式中:K为无量纲弹嵌常数。
由式(24)计算得一阶频率系数,列于表2。K分别趋近于0 和∞时,弹性嵌固梁振型分别趋近于简支梁振型和固支梁振型。取K值为30,将式(23)代入式(3),由式(14)~(19)计算得到储液结构动力特性参数,见表3。此处主要考虑双向梁一阶振型,故求得的圆频率ω 为一阶圆频率(简称“基频”)。

表2 弹性嵌固梁一阶频率系数Table 2 First order frequency coefficient value of elastic embedded beam

表3 储液结构动力特性参数Table 3 Dynamic characteristic parameters of the LSS
将图4 得到的5 组输入加速度信号作为地震动x¨g(t) 代入式(21),并基于Maple 软件通过数值方法进行积分运算,可得储液结构动力响应广义坐标X(t)。将其代入式(3),可得壁板(y,z)处挠度响应xs(y,z,t),进而横向应变εy(y,z,t)可计算为
将试验测得的输入加速度x¨g(t) ,计算得到的挠度响应xs(y,z,t)代入式(8),可求得壁板(y,z)处动水压力p(y,z,t)。至此,可对比计算值与试验数据以验证理论。结构应变、动水压力时程曲线分别如图5(a)~(e)、图6(a)~(e)所示,图5(f)、图6(f)分别标注了该两种响应峰值计算值与试验值相对误差的绝对值。可以发现,理论计算得到的曲线变化趋势与实测数据较一致,且两者峰值相差均在15%以内。其中,摆锤高度H1时误差较大,可能的原因是该工况下地震荷载幅值较小,试验数据信噪比较低。该工况之外,结构应变计算相对误差低于10%,而动水压力计算相对误差低于5%。
3 算例分析
通过本文提出的理论方法进行算例分析,以上述模型试验典型矩形储液结构为例,求解其在爆炸地震动下的动力响应,并构建以最大挠度为指标的爆炸冲击响应谱。选取3 种典型加速度波形用以构造爆炸冲击地震动[1,29]。
(1) 半正弦加速度波形。该类型波形形式简单,在理论分析时便于进一步求解结构动力响应解析表达式,且可从波形和作用效果两方面等效爆炸冲击震动信号,其加速度时程表达式为
式中:e1=exp(-7.2t/t0),e2=exp[1.15(t0-t)/t0],s1=sin(4.712e2t/t0),c1=cos(4.712e2t/t0)。
(3) 类型Ⅱ加速度波形。该类型波形代表岩土介质中爆炸震动区的典型波形,可用于描述跨地震区和亚地震区的爆炸冲击震动,岩土介质震动位移完全恢复,其加速度时程为
式中:e3=exp[-5.7(t/t0)2],e4=exp[0.7(t0-t)/t0],s2=sin(15.708e2t/t0),c2=cos(15.708e2t/t0)。该3 种典型爆炸地震动波形的归一化加速度时程曲线如图7 所示。

图7 典型爆炸地震动波形的归一化加速度时程曲线Fig.7 Normalised acceleration time-history curves of typical explosion-induced ground shock waveforms
3.1 储液率的影响
保持结构尺寸特征不变而改变储液率(Hl/Hs),由无液状态(Hl=0)逐渐增加至满液状态(Hl=Hs),进而分析储液率的影响。随着储液率的增加,广义质量和激励因子的变化分别如图8和图9 所示。可以看出,结构广义质量和结构激励因子保持恒值,液体广义质量与液体激励因子在储液率为0.3 之前变化不大,而后增势逐渐增加。在前两者叠加作用下,体系广义质量、体系激励因子与液体项增势相同。

图9 激励因子随储液率的变化Fig.9 Variation in excitation factor with liquid filling ratio
随着储液率的增加,结构广义刚度k*、基频ω0、特征因子F˜ 的变化如图10 所示。可以看出,结构广义刚度保持不变。由于体系广义质量随储液率提高先缓慢后加速增加,基频随之先变化不大后加速降低。特征因子先增加后减小,这主要取决于激励因子与广义质量的相对关系:一方面,液体激励因子增加使特征因子趋于增加;另一方面,液体广义质量的增加使特征因子趋于减小。两者综合作用,储液率为0.8 时特征因子达到最大值2.34。

图10 广义刚度、基频、特征因子随储液率的变化Fig.10 Variation in generalised stiffness, fundamental frequency, and characteristic factors with liquid filling ratio
为进一步探讨储液率的影响,对储液率为0、0.4、0.8 时储液结构动力响应进行分析。在3 种典型爆炸冲击地震动(参数取A0=5g,t0=5 ms)作用下,储液结构顶部中心挠度响应如图11 所示。可以看出,在同一地震动作用下,随着储液率增加,储液结构挠度响应表现出不同特点。首先,储液增加使液-固体系基频降低,提高了结构振动周期,在同一地震动下动力响应相位、幅值发生变化;其次,储液增加改变了特征因子,由式(21)可知,这表明同一地震动作用引起的某一特定频率结构的动力响应幅值发生改变。

图11 不同储液率下储液结构挠度时程曲线Fig.11 Deflection time-history curves of the LSS with different liquid filling ratios
3.2 地震动要素的影响
以图7 所示的3 种波形为基础,先后在加速度持时t0为5 ms 的条件下改变峰值A0:5g、10g、15g,以及在加速度峰值A0为5g的条件下改变持时t0:5、10、15 ms,以分析地震动波形与该两种参数的影响。同时,3.1 节分析表明,所研究储液结构在储液率为0.8 时处于不利条件,即经受爆炸地震动时有可能发生较大的动力响应。因此,本节分析中按此储液状态进行计算。随地震动加速度峰值的改变,储液结构顶部中心挠度响应如图12 所示。可以看出,随着加速度峰值提高,储液结构挠度响应变化趋势不变,而幅值线性提高。究其原因,本文中理论分析假设结构变形在弹性范围内,且忽略液体晃动产生的非线性影响,某一特定储液结构在储液状态不变时,其动力特性不变,地震动波形、持时不变而峰值改变时,由式(21)可知结构响应随之线性变化。
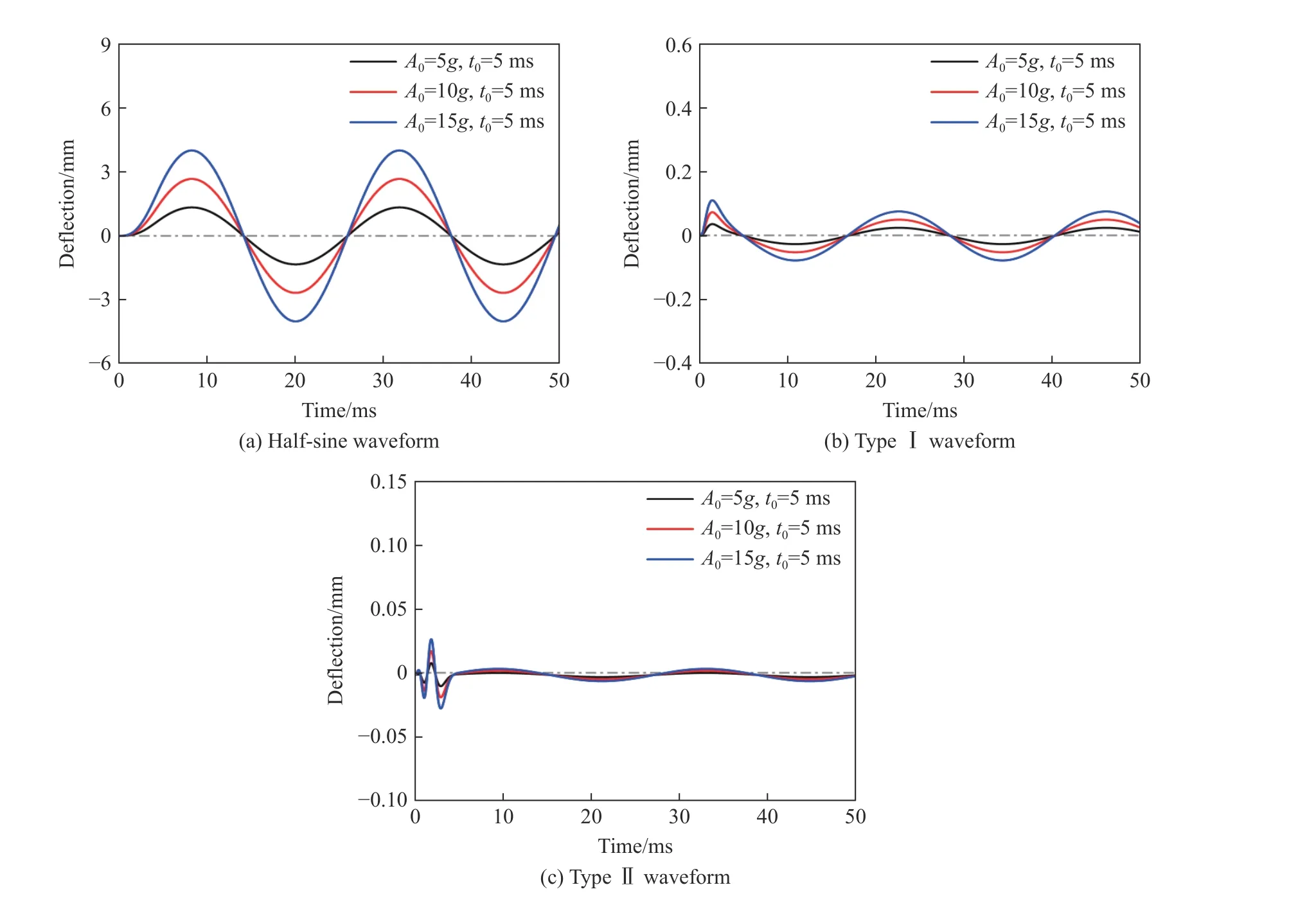
图12 不同地震动加速度峰值下储液结构挠度时程曲线Fig.12 Deflection time-history curves of the LSS under ground shocks with different peak accelerations
随地震动加速度持时的改变,储液结构顶部中心挠度响应如图13 所示。可以看出,随着加速度持时增加,储液结构挠度响应变化趋势、幅值均有所改变。究其原因,地震动波形、峰值不变而持时改变时,其频谱特性发生改变,因而激发动力特性未变的储液结构产生不同的响应,对应为式(21)积分项发生非线性变化。
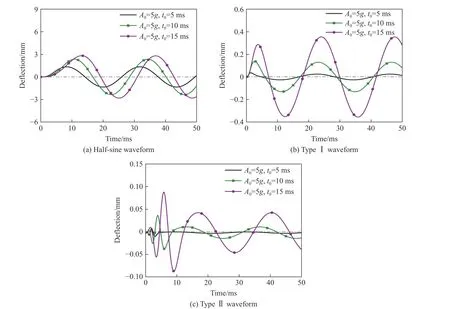
图13 不同地震动加速度持时下储液结构挠度时程曲线Fig.13 Deflection time-history curves of the LSS under ground shocks with different acceleration durations
此外,由图11~13 可以发现,当地震动加速度峰值、持时不变而波形改变时,储液结构动力响应变化趋势呈现较大的区别,而响应幅值存在数量级上的差异。究其原因,储液结构动力特性维持不变,而该3 种波形的频谱特性差别较大,故引起的结构动力响应不同。
3.3 构建动力响应谱
出于防护工程需要,考虑爆炸冲击作用下最不利因素,有必要构建动力响应谱,得到储液结构有可能发生的最大动力响应。改变加速度峰值A0和持时t0并通过式(21)~(22)计算,可以得到储液结构在图7 所示3 种典型爆炸冲击地震动作用下的标准化动力响应谱,如图14 所示。出于对比需要,图中绘制了在集中参数的单自由度(single-degree-of-freedom, SDOF)体系下构建的动力响应谱,即式(21)等式右侧特征因子F˜ 为1 时得到的响应谱。可以看出,考虑分布弹性的广义单自由度体系(generalised singledegree-of-freedom, generalised SDOF)与考虑集中参数的单自由度体系,二者的差别由特征因子F˜ 表征,而在本研究中,F˜ 的取值由储液结构特征(尺寸、密度、刚度、振型)与内储液体特征(储液率、密度)所决定,体现了流固耦合作用效果。例如图10 反映出,与无液条件相比,流固耦合作用使储液结构动力响应增强,而以储液率0.8 为界,增强的程度先提高后降低。

在矩形储液结构模型储液率为0.8 的条件下,半正弦波形、类型I 波形、类型Ⅱ波形的最大动力响应相对于等效静载响应分别提高至1.77、2.52、4.60 倍。考虑该3 类波形的背景条件,发现考虑土-结构相互作用而产生的具有震荡特征的地震动,对储液结构安全性威胁更大。同时,需要注意的是,以响应谱峰值辅助结构设计与选型是安全保守的。该3 类波形响应谱峰值对应的t0/Tn不同,考虑t0与爆距相关[1],故响应谱峰值高并不一定引起绝对的高幅值响应。若考虑工程结构设计的经济性,还要在合理估计爆炸参数取值范围后,按本文方法作具体分析。
4 结 论
将储液结构近似为具有分布弹性的广义单自由度体系,基于薄板振动理论和虚功原理建立运动方程,通过Rayleigh 法、Duhamel 积分法分别计算结构振动频率、动力响应,进而构建爆炸冲击震动下储液结构动力响应谱。提出的方法具有理论简单、针对性强的特点,得到的主要结论有:
(1) 无量纲地震动激励特征因子(简称“特征因子”)为液-固体系激励因子与广义质量之比,反映广义单自由度体系相较于集中参数单自由度体系的差别,亦可用于评价流固耦合作用对储液结构地震响应的影响;
(2) 将横向两端弹性嵌固梁和竖向剪切型悬臂梁函数组合,得到适用于储液结构模型的壁板振型;利用爆炸冲击震动模拟平台开展钢制储液结构模型试验,得到5 种冲击地震动强度下结构变形应变、动水压力时程;将实测地震动加速度等效为外部荷载进行数值计算,计算结果与试验数据在曲线变化趋势和峰值方面较一致,理论方法得到验证;
(3) 以储液结构模型为例,计算分析储液率和地震动加速度峰值、持时、波形等要素对结构动力响应的影响,结果表明,随储液率增加,特征因子先提高后小幅降低,在储液率为0.8 时达到最大值2.34,此时受地震动作用易发生较大动力响应;随储液率增加,结构振动基频减小,同一地震动下响应幅值和相位发生变化;弹性范围内,结构响应幅值随地震动加速度峰值线性变化;地震动加速度持时、波形改变引起频谱特性改变,致使结构响应发生非线性变化;
(4) 构建爆炸冲击震动下储液结构挠度响应谱,满足工程设计初步快速计算的要求;以典型加速度波形构造的爆炸地震动,其作用效果可分为相对于等效静力作用的缓和区、增强区和等效区,将响应谱峰值作为最不利响应用于防护工程设计偏于保守。
提出的理论方法适用于薄板范畴任意矩形储液结构,壁板形状函数的合理假设对于提高计算精度十分关键;在评估场地爆炸震动参数范围的基础上,结合本文理论方法进行计算,可提高工程设计的经济性。

