堰塞坝溃口及洪峰参数模型评估与优化

焦煦 冯震宇 廖海梅

摘 要：由滑坡等失稳地质体快速堆积并堵塞河道形成的堰塞坝溃决后会对下游人民生命财产安全造成极大威胁。建立快速准确的溃决参数预测模型，是制定有效防灾减灾措施的必要条件。本文收集了75例包含坝高、库容、溃口峰值流量、坝体冲蚀系数等参数的堰塞坝案例，基于均方根误差、回归相关系数、百分比偏差三个指标对具有代表性的土石坝和堰塞坝参数模型进行评估。通过回归分析建立新的堰塞坝溃口深度预测模型及溃口峰值流量预测模型，将新建模型与现有模型对比，在实际案例中验证了模型的适用性。研究结果表明：现有模型中单参数、双参数及土石坝模型对于堰塞坝溃决参数预测效果不佳，考虑坝体易蚀性的参数模型具有较高准确性，本文所建新模型预测效果有所提升，使用范围更广，预测结果可为堰塞坝的防灾减灾措施提供参考。

关键词：堰塞坝；溃口峰值流量；溃口深度；参数模型

中图分类号：TV122.4

文献标志码：A

堰塞坝是一种由地震或强降雨等引发滑坡堵塞河道而形成的天然堆积体，通常由松散、易侵蚀的材料组成，没有专门设计的溢洪道，极易发生漫顶溃决，从而形成具有强大冲击力的含沙洪水^［1］。因此，堰塞坝通常具有寿命短、峰值流量大的特点。石振明等^［2］对国内外276例堰塞坝寿命进行统计分析，表明86％的堰塞坝在形成一年内发生溃决。1786年，四川省康定地区地震引发滑坡堵江形成的堰塞坝于10天后溃决，洪水不仅冲毁下游基础设施，还造成了近10万人死亡^［3］。1933年，叠溪海子堰塞坝溃决，使断流一个多月的岷江突发洪水，冲毁下游两岸农舍田地，造成约2 500人丧生^［4］。2000年，易贡巨型滑坡堰塞坝在形成后两个月溃决，峰值流量高达124 000 m3/s，超过50万人的房屋以及道路等大量人工设施被冲毁^［5］。2018年，“11.3”金沙江白格堰塞坝在形成数天后发生溃决，下游受灾人数约5.4万人，房屋损毁3 000多间，农田受灾面积约30 km2，直接经济损失高达74亿元^［6］。因此，建立快速准确的溃决参数预测模型，对制定有效的防灾减灾措施具有重要意义。

溃口峰值流量对下游受灾程度有着决定性作用，而溃口深度决定下泄水量的多少，进而影响溃口峰值流量。国内外学者在坝体几何特征、坝体材料特征、库水条件对溃口深度和溃口峰值流量影响等方面展开了研究。1985年，COSTA^［7］根据10座堰塞坝溃决案例，第一次提出了考虑坝高和库容的溃口峰值流量参数预测模型；随后COSTA和SCHUSTER^［8］引入了势能的概念（势能=坝高×库容×水的容重），基于12座堰塞坝提出了新的溃口峰值流量预测参数模型。1997年，WALDER与O′CONNOR^［9］基于14座堰塞坝提出了以水位下降高度和库容为变量的溃口峰值流量参数预测模型。2014年，HAKIMZADEH等^［10］根据物理试验数据提出新的考虑坝高、库容的溃口峰值流量参数预测模型，并采用37组实际案例验证了模型的适用性。上述参数模型参考案例数较少，并且仅考虑了少量的堰塞坝几何参数与库容条件影响，也未考虑坝体材料特征。2012年，PENG和ZHANG^［11］将45个堰塞坝划分为高度易蚀性、中度易蚀性、低度易蚀性，建立了考虑堰塞坝形态、上游水动力条件、材料冲蚀特性的溃口深度参数预测模型及溃口峰值流量参数预测模型；2014年，石振明等^［2］基于新的堰塞坝溃决案例和相似的统计分析方法，也提出了相应的溃口峰值流量及溃口深度参数预测模型。上述侵蚀度的划分基于土壤侵蚀率和溃口流速或水流剪切力的关系，这种方法在确定堰塞坝侵蚀度的应用过程中存在一定的困难和主观性^［12］。2022年，单熠博等^［13］提出了堰塞坝类型（土质型、混合型、块石型）的定量划分指标，选择堰塞坝高度、宽度、库容及坝料冲蚀特性等参数，建立了溃口峰值流量参数的快速预测模型。但该模型中的冲蚀参数取值取决于坝体颗粒组成，而现有技术尚难以获得详细的坝体表面及内部物质信息，故在实际应用中也受到一定限制。现阶段堰塞坝溃口深度及洪峰参数模型参考案例数较少、考慮因素较少或冲蚀参数难以确定。因此，本文根据所收集的堰塞坝溃决案例，对堰塞坝参数模型和土石坝参数模型进行分析评估，并提出新的堰塞坝溃决参数预测模型。

1 现有堰塞坝溃决参数模型的评价

堰塞坝溃决参数模型涉及的参数主要为坝长L_d、坝宽W_d、坝高H_d、坝体体积V_d、库容V_l、溃口顶宽W_t、溃口底宽W_b，如图 1所示。

1.1 现有堰塞坝溃决参数模型

溃口峰值流量及溃口深度是反映堰塞坝溃决灾害程度的两个重要参数。针对溃口峰值流量的预测，本文分别对较具代表性的单参数模型^［7］、双参数模型^［7］、及多参数模型^［2，11］进行评价分析，并选取具有代表性的土石坝双参数模型^［10］研究人工土石坝参数模型对堰塞坝溃决参数预测的适用性；对于溃口深度的预测，则对预测效果相对较好的两个多参数模型^［2，11］进行评价分析。各溃决参数模型具体如表1所示。

1.2 现有模型的评估

1.2.1 评估方法

本文共收集了75个堰塞坝案例，包含坝高、库容、溃口峰值流量、坝体冲蚀系数等参数，用于溃口峰值流量参数模型的评价，其中包含溃口深度数据的有23组案例，进行溃口深度参数模型评价。由于篇幅原因，文中只列举75组案例中包含溃口深度数据的23组堰塞坝案例，见表2。拟利用表1的预测模型计算各案例的溃决峰值流量及溃口深度，并通过绘制散点图观察分析和定量评估两种方法对不同模型的计算结果进行评估。

定量分析可以客观描述各模型的精度，本文采用回归相关系数R2、均方根误差E_RMS、百分比偏差P_BIAS三个指标对各模型进行定量评价。其中，回归相关系数R2可反映实测数据与拟合函数之间的吻合程度，R2值越接近于1，表示预测值与实际值相关程度越高。均方根误差E_RMS统计模型预测值与实际值之间的偏差，可在一定程度上反映模型的整体精度，其值越小，则表示模型计算效果越好。百分比偏差P_BIAS可反映预测值相对于实测值偏大或者偏小的趋势^［14］。三个评价指标的表达式分别为：

式中，Y_i为因变量实测值；Y_j为因变量预测值；Y_ave因变量实测值的平均值；n为案例数。各评价指标的评价标准如表3所示^［14］。

1.2.2 不同溃口深度参数模型的评价结果

根据所收集到的23例包含溃口深度数据的堰塞坝资料，计算各模型下堰塞坝溃口深度预测值，散点图评价结果如图2所示，图中斜线表示预测值与实际值相等，为最佳线。

计算不同类型溃口深度参数模型的三个评价指标评价结果如表4所示。

在溃口深度参数预测模型中，PENG等多参数简化模型和石振明等多参数简化模型考虑因素均为坝高、库容、坝体冲蚀系数。由表4可知，PENG等多参数简化模型的均方根误差E_RMS与百分比偏差P_BIAS在极好范围内，说明该模型预测值不会出现极大或者极小的情况；石振明等多参数简化模型的均方根误差E_RMS与百分比偏差P_BIAS分别在极好与一般范围；两种模型的回归系数R2分别为0.15与0.5，说明两种溃口深度预测模型预测值与实测值相关性较差，预测效果不佳。从图2也可看出，根据两种溃口深度模型计算的本文堰塞坝案例预测值与实际值均存在较大差别。石振明等多参数简化模型的溃口深度预测值大多是实测值的0.5倍，而PENG等多参数简化模型的溃口深度预测值也普遍低于实测值。

1.2.3 溃口峰值流量参数模型的评价结果

通过所收集的堰塞坝资料，计算各模型下堰塞坝溃口峰值流量预测值，散点图评价结果如图3所示。

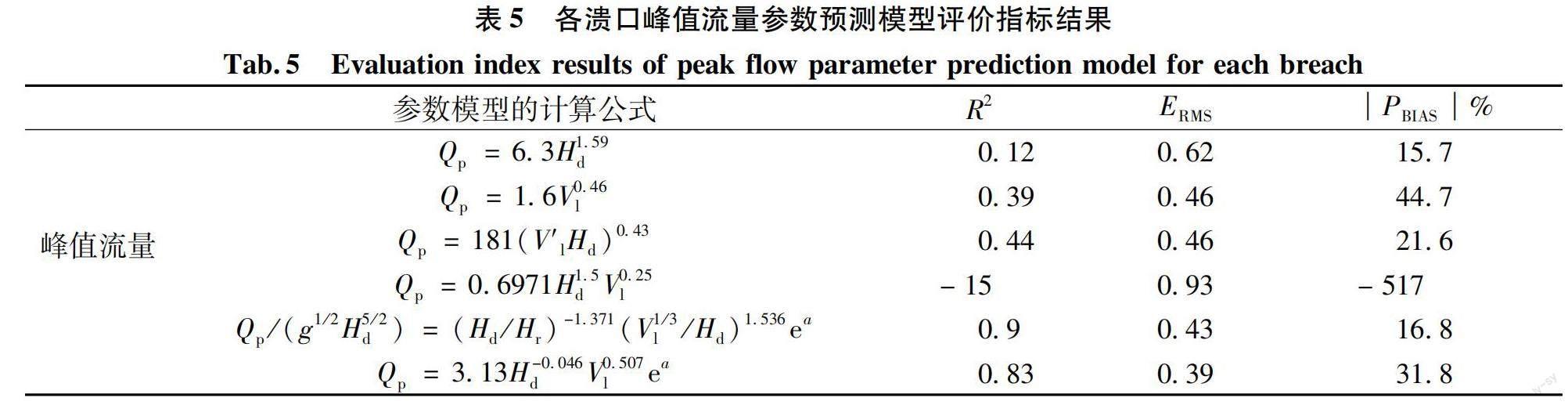
根据75例堰塞坝资料，计算不同类型溃口峰值流量参数预测模型的三个评价指标的评价结果如表5所示。

从表5的评价结果分析可知，坝高或库容的单参数模型对本文75个堰塞坝案例的峰值流量预测效果较差。虽然坝高单参数模型的P_BIAS值处于极好范围内，但其回归系数R2值仅为0.12，效果较差，E_RMS值也仅处于合格范围。库容单参数模型的R2值在合格范围，E_RMS、P_BIAS均在一般范围。从图3（a）中也可看出两种单参数模型的散点图分布远离最佳线，尤其是溃口峰值流量实测值低于1 000 m3/s时，预测效果与实测值出现较大偏差。

坝高、库容双参数模型的R2、E_RMS、P_BIAS分别处于合格、一般、极好的范围，与单参数模型相比，预测效果有所提升，但模型预测值与实际值相关性仍然不高。同时，从图3（b）中可看出该模型对于较大的峰值流量，比如峰值流量超过30 000 m3/s时，预测值普遍低于实际值。土石坝的双参数模型对堰塞坝案例的评价结果较差，其值为负值，预测值与实际值基本无相关性，这很可能是由于该模型基于物理试验数据建立，对真实堰塞坝溃决流量预测具有局限性。从图3（b）中也可看出该模型的散点主要分布在最佳线上部，预测值普遍高于实际值，这很可能是由于物理试验的人工土石坝在溃决后一般不会存在残余坝高，而堰塞坝结构组成一般为非均质坝，发生漫顶溃决后通常存在残余坝高，故用土石坝模型预测堰塞坝溃口峰值流量的结果偏高。

引入坝体冲蚀系数后，PENG等多参数简化模型的R2为0.9，模型相关程度极好，相较于单参数与双参数模型有了很大提升，其E_RMS值与P_BIAS值分別在较好与极好范围。石振明等多参数简化模型的R2与P_BIAS值略低，但也在较好范围内。从定量评价结果来看，PENG等多参数简化模型的预测精准性最好。从图3（c）中可看出两种模型对较大峰值流量的预测效果有所提升，但当峰值流量低于1 000 m3/s时，数据点并未分布在最佳线附近，预测效果不佳。

据此，本文将选择合适的坝体几何参数、采用更方便的坝体易蚀性划分方法，建立新的溃口深度与溃口峰值流量预测模型。

2 堰塞坝溃决参数模型的建立

2.1 溃口深度参数预测模型

坝高是反映堰塞坝几何形态的一个重要特征参数，坝高越高，水头势能越大，发生漫顶以后，冲刷坝体的水流流速也可能越大，从而形成较大的溃口深度。库容是影响堰塞坝溃口深度的一个关键参数，库容越大，冲刷形成的溃口及溃决下泄洪水量也越大。坝体材料是影响溃口发展的另一关键参数，但现有预测模型采用的坝体易蚀性划分方法存在一定的主观性，实用性受到限制^{［2，11，13］}，故本文参考CUI等^［15］根据坝体颗粒组成划分堰塞坝危险性的方法，将堰塞坝易蚀性分为高、中、低三种，分别以字母H、M、L代表，其中，坝体物质组成以土质为主时为高易蚀性，土石混合时为中易蚀性，以块石为主时为低易蚀性。

本文采用多元回归分析方法，选择坝高、库容、坝体易蚀性三个因素建立溃口深度参数预测模型，其基本数学方程为：

y=f（x₁，x₂，…，x_k;β₁，β₂，…，β_p）+ζ（4）

式中，f为非线性函数；y为模型的因变量（即溃口深度）；x₁，x₂，…，x_k为模型的回归系数；β₁，β₂，…，β_p为模型的自变量（即坝高、库容、坝体易蚀性）；ζ为模型误差项。对具有溃口深度的23组堰塞坝进行多元回归分析，得到溃口深度参数预测模型表达式：

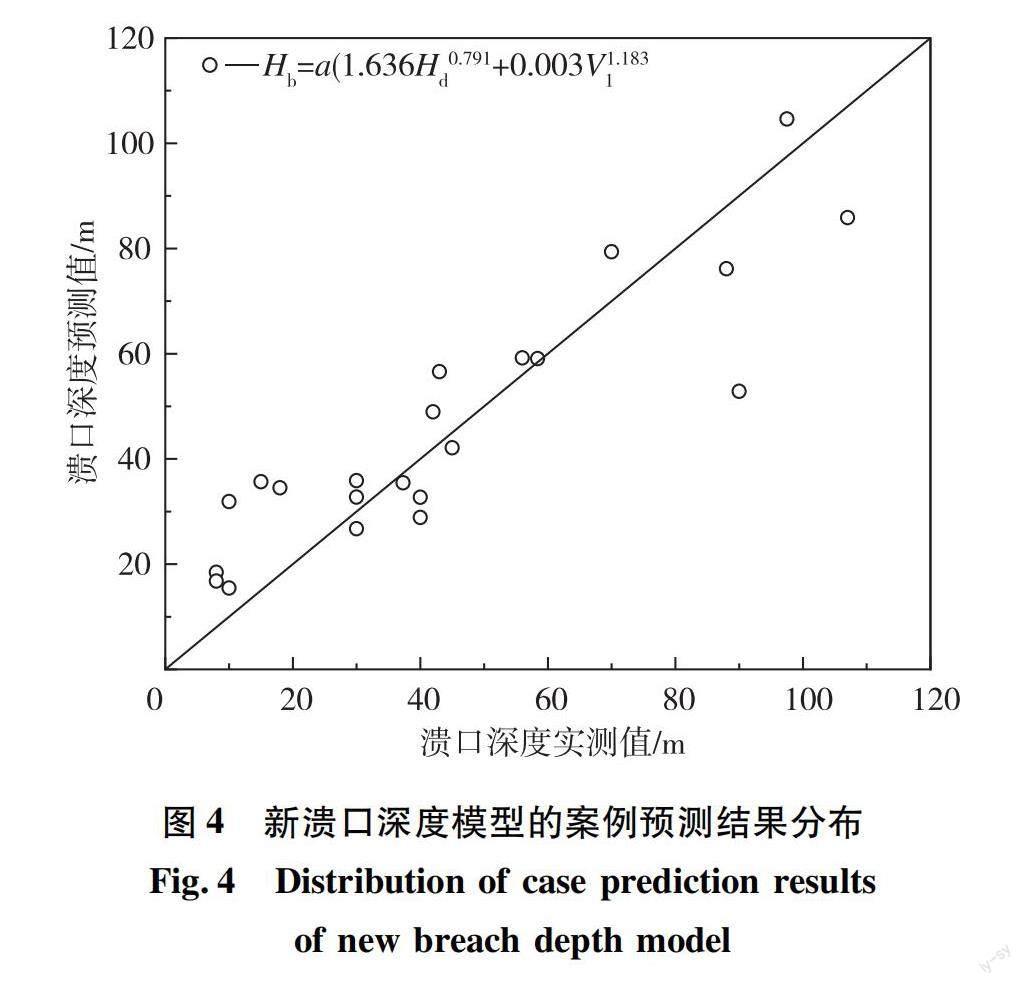
H_b=a（1.636H^0.791_d+0.003V^1.183_l）（5）

式中，a为侵蚀系数。根据SPSS软件输出结果知，当堰塞坝组成以土质为主时（高易蚀性），a取0.732；当堰塞坝组成为混合型时（中易蚀性），a取0.883；当堰塞坝组成以块石为主时（低易蚀性），a取0.694。

采用式（1）、（2）、（3）对该溃口深度参数预测模型进行计算，得到回归系数为0.8，处于较好范围内，较PENG等及石振明等溃口深度参数模型分别提升了433％、60％。均方根误差E_RMS值为0.19，百分比偏差P_BIAS为3.8％，两者均处于极好范围内，说明本模型预测结果与实测值误差较小，很少出现与实测值偏差很大的情况。图4的散点图也表明大部分数据分布在最佳线附近，预测值与实际值比较接近，预测精度较好。

2.2 溃口峰值流量参数模型

坝高、库容与溃口深度是影响溃口峰值流量的关键参数。国内外学者通过物理模型试验研究坝高、库容对溃口峰值流量的影响。ZHU等^［16］通过开展4组水槽试验分析了堰塞坝高度对峰值流量的影响，表明溃口峰值流量随坝体高度减小而降低。付建康等^［17］通过5组模型试验数据分析发现库容越大，溃口峰值流量越大，溃决时间持续越长。而溃口深度越大，下泄水量及峰值流量也越大。因此，本文选择坝高、库容、溃口深度三个影响因素，由于具有溃口深度的案例仅有23例，先對溃口深度未知的52组案例采用式（5）进行计算溃口深度，然后参照溃口深度预测模型采用非线性多元回归分析方法建立溃口峰值流量参数预测模型。

根据《水利水电枢纽工程等级划分及设计标准》，可将坝体分为高、中、低三种类型^［18］，70 m以上为高坝，30～70 m为中坝，小于30 m为低坝。堰塞坝坝高差别较大，本文收集的案例坝高在4.3～274 m之间，故参照上述标准将堰塞坝分为高坝、中坝、低坝。得到的溃口峰值流量参数预测模型如下：

高坝Q_p=10.03H^2.816_dV^1.557_lH^－3.661_b（H_d＞70）（6）

中坝Q_p=H^1.629_dV^0.826_lH^－0.053_b（30≤H_d≤70）（7）

低坝Q_p=194.7H^1.163_dV^－0.084_lH^－0.636_b（H_d＜30）（8）

式中，Q_p为溃口峰值流量m3/s；H_d为坝高，m；V_l为库容，106m3；H_b为溃口深度，m。

采用式（1）、（2）、（3）对该峰值流量预测模型进行计算，得到回归系数R2为0.85，处于较好范围内，较坝高单参数、库容单参数、坝高库容双参数、石振明等多参数简化模型分别提升了608％、118％、70％、2.4％。尽管比PENG等多参数简化模型的R2略低，但其均方根误差E_RMS（0.36）较PENG等多参数简化模型降低16.3％，百分比偏差P_BIAS（13.3％）较PENG等多参数简化模型降低58.2％，说明本文提出的模型预测值与实测值误差更小。从图5的散点图也可观察到预测值与实测值偏差不大，且对特大溃口峰值流量的预测效果依然很好。可见，本模型整体预测效果较好，适用性较强。

3 案例分析

为了验证本文所建立的堰塞坝溃口深度及溃口峰值流量参数模型的准确性，选择本文数据库外的两个案例进行分析，并与不同学者提出的参数模型进行对比。

3.1 “10.10”白格堰塞坝

2018年10月10日，西藏自治区昌都市和四川省甘孜自治州交界处的金沙江河道右岸发生山体滑坡，堵塞了金沙江干流，形成白格堰塞坝^［19］。坝体主要物质组成为碎石土加块石，坝体压实性较好，并具有一定的隔水性质^［20］。因此，在预测溃决参数过程中易蚀性取中易蚀性。坝体呈左高右低，坝高约61 m，库容约2.9亿m3，溃决峰值流量约10 000 m3/s。溃决后堰塞体右岸被冲出的水槽深约55 m^［21］。不同模型的溃决参数预测结果如表6所示，可看出石振明等多参数模型的溃口深度预测值约为真实值的0.5倍，PENG等多参数简化模型的预测值也小于实际值。而对溃口峰值流量的预测，多参数模型预测效果优于单参数或双参数模型，但多参数模型的预测值均小于实际值，预测结果偏危险。根据本文提出的预测模型计算，得到溃口深度为39.49 m，溃口峰值流量为11 613.2 m3/s，与实际值相对误差分别为-27.3％、16.1％，表明溃口深度预测值小于实测值，溃口峰值流量预测值大于实测值。预测结果误差相对较小，预测结果偏保守，有助于制定更安全的堰塞坝抢险处置方案。

3.2 “11.3”白格堰塞壩

“11.3”白格堰塞坝为上述“10.10”白格堰塞坝原处滑坡再次发生崩塌，覆盖残余坝体所形成，坝体材料特性取中易蚀性，顶宽约195 m，长273 m，坝高约96 m。进行人工干预开挖导流槽后堰塞坝库容为5.78×108 m3^［22］。由于人工开挖了导流槽故不进行溃口深度预测值与实际值比较，并且在溃口峰值流量计算时溃口深度取预测溃口深度值。

不同模型溃决参数预测结果如表7所示。可以看出，坝高或库容单参数模型预测结果与实际值相差较大，坝高、库容双参数模型预测精度虽有所提升，但与实际值的相对误差仍大于30％，PENG等多参数简化模型及石振明等多参数简化模型考虑了坝体冲蚀系数，预测效果较好，预测值与实际值相对误差绝对值均在30％以内。根据本文提出的预测模型计算，得到溃口峰值流量为26 880.2 m3/s，与实际值相对误差为-13.2％，预测精度较前人模型有所提升，更高的预测精度有利于更精准地制定堰塞坝防灾减灾措施。

4 结论

本文根据所收集的堰塞坝溃决案例对不同学者所提出的溃决参数模型进行对比分析，并提出新的溃口深度及峰值流量预测模型。得出如下结论：

（1）对于溃口深度的预测，由于包含溃口深度数据的堰塞坝案例较少，故现阶段溃口深度参数预测模型预测效果不佳，预测结果普遍低于实际值。对于溃口峰值流量的预测，与单参数或双参数模型相比，考虑坝体易蚀性的多参数模型R2均大于0.8，处于较好以上范围，预测精度更高。

（2）本文所提出的新的溃口深度参数预测模型，回归系数为0.8，较PENG等及石振明等溃口深度参数模型分别提升了433％、60％。均方根误差E_RMS与百分比偏差P_BIAS均处于极好范围内。

（3）从文中案例分析可知，对于溃口深度预测，本文预测模型误差均在±30％以内。在将堰塞坝划分为高、中、低三种类型的基础上，提出了考虑溃口深度的溃口峰值流量参数模型，其R2为0.85、E_RMS为0.36、P_BIAS为13.3％，模型整体拟合效果有所提升。从文中案例分析可知，新模型对溃口峰值流量的预测误差均在±20％以内，与其他模型相比预测精度更高。

参考文献：

[1]ZHOU M， ZHOU G G D， CUI K F E， et al. Influence of inflow discharge and bed erodibility on outburst flood of landslide dam［J］. Journal of Mountain Science， 2019， 16（4）： 778-792.

［2］ 石振明， 马小龙， 彭铭， 等. 基于大型数据库的堰塞坝特征统计分析与溃决参数快速评估模型［J］.岩石力学与工程学报， 2014， 33（9）： 1780-1790.

［3］ DAI F C， LEE C F， DENG J H， et al. The 1786 earthquake-triggered landslide dam and subsequent dam-break flood on the Dadu River， southwestern China［J］. Geomorphology， 2005， 65（3-4）： 205-221.

［4］ 王兰生， 杨立铮， 李天斌， 等. 四川岷江叠溪较场地震滑坡及环境保护［J］. 地质灾害与环境保护， 2000， 11（3）： 195-199.

［5］ 袁浩， 郭长宝， 吴瑞安， 等. 西藏易贡高位远程滑坡研究进展与展望 [J/OL]. 地质通报， 2021： 1-19[2023-06-15].http：//kns.cnki.net/kcms/detail/11.4648.P.20211227.1821.004.html.

［6］ 张新华， 薛睿瑛， 王明， 等. 金沙江白格滑坡堰塞坝溃决洪水灾害调查与致灾浅析［J］. 工程科学与技术， 2020， 52（5）： 89-100.

［7］ COSTA J E. Floods from dam failures［M］. Washingtow D C： US Geological Survey， 1985.

［8］ COSTA J E， SCHUSTER R L. The formation and failure of natural dams［J］. Geological society of America bulletin， 1988， 100（7）： 1054-1068.

［9］ WALDER J S， O'CONNOR J E. Methods for predicting peak discharge of floods caused by failure of natural and constructed earthen dams［J］. Water Resources Research， 1997， 33（10）： 2337-2348.

［10］HAKIMZADEH H， NOURANI V， AMINI A B. Genetic programming simulation of dam breach hydrograph and peak outflow discharge［J］. Journal of Hydrologic Engineering， 2014， 19（4）： 757-768.

［11］PENG M， ZHANG L M. Breaching parameters of landslide dams［J］. Landslides， 2012， 9（1）： 13-31.

［12］阮合春， 陳华勇， 李霄， 等. 基于新样本的滑坡坝溃决洪峰流量预测模型修正与对比［J］. 科学技术与工程， 2022， 22（20）： 8606-8615.

［13］单熠博， 陈生水， 钟启明， 等. 考虑颗粒组成的堰塞体溃口峰值流量快速预测模型［J］. 应用基础与工程科学学报， 2023， 31（3）： 584-598.

［14］齐子杰， 黄卫， 汪利先， 等. 堰塞坝溃决参数模型评估与优化分析［J］. 人民长江， 2022， 53（12）： 157-166.

［15］CUI P， ZHU Y Y， HUA Y S， et al. The 12 May Wenchuan earthquake-induced landslide lakes： distributi on and preliminary risk evaluation［J］. Landslides， 2009， 6（3）： 209-223.

［16］ZHU X H， LIU B X， PENG J B， et al. Experimental study on the longitudinal evolution of the overtopping breaching of noncohesive landslide dams［J］. Engineering Geology， 2021， 288： 106-137

［17］付建康， 罗刚， 胡卸文. 滑坡堰塞坝越顶溢流破坏的物理模型实验［J］. 吉林大学学报（地球科学版）， 2018， 48（1）： 203-212.

［18］杨忠勇， 罗铃， 杨百银， 等. 土石坝溃决过程中溃口发展及溃坝洪水计算方法探讨［J］. 水力发电， 2019， 45（9）： 43-47.

［19］余志球， 邓建辉， 高云建， 等. 金沙江白格滑坡及堰塞湖洪水灾害分析［J］. 防灾减灾工程学报， 2020， 40（2）： 286-292.

[20]栾约生， 石纲， 张亮， 等. 金沙江白格堰塞坝溃决模式与冲刷进程分析[J]. 湖南水利水电， 2022（3）： 72-74.

[21]侯精明， 马利平， 陈祖煜， 等. 金沙江白格堰塞湖溃坝洪水演进高性能数值模拟[J]. 人民长江， 2019， 50（4）： 8-11， 70.

[22]赵磊， 史正涛， 叶蕾， 等. “11·03”金沙江白格堰塞湖溃决洪水沉积物粒度特征[J/OL]. 沉积学报： 1-15[2023-08-28]. https：//kns.cnki.net/kcms/detail/detail.aspx？FileName=CJXB20221122000&DbName=CAPJ2022. DOI：10.14027/j.issn.1000-0550.2022.145.

（责任编辑：于慧梅）

Evaluation and Optimization of Landslide Dam Breaking and Flood Peak Parameter Models

JIAO Xu， FENG Zhenyu， LIAO Haimei*

（College of Civil Engineering， Guizhou University， Guiyang 550025， China）

Abstract： Landslide dams are generally caused by the fact that unstable geological bodies like landslide quickly accumulate and block rivers， which pose a great threat to the safety of people's life and property in the downstream area after the breach. Therefore， establishing a fast and accurate prediction model of breach parameters is necessary for hazard prevention and mitigation. In this paper， 75 cases of landslide dam failure including parameters like dam height， reservoir capacity， peak discharge of breach and erosion coefficient of dam body were collected. The mean square error E_RMS， correlation coefficient R2 and percentage deviation P_BIAS were used to compare and analyze the prediction effect of representative parameter models of earth-rock dam and landslide dam. Through regression analysis， a new prediction model of dam breach depth and peak discharge is established， and the new model is compared with the existing models. Finally， the applicability of the model is verified in actual cases. The results show that the single parameter， double parameters and earth-rock dam models in the existing models are not effective in predicting the dam break parameters， but the parameter model considering the erosivity of the dam has high accuracy. The prediction effect of the new model established in this paper has been improved with wider application， and the prediction results can provide theoretical reference for disaster prevention and mitigation measures of landslide dams.

Key words： landslide dam; peak discharge; depth of breach; parameter model