基于非平衡相间传质的多梯度钻井井底压力预测

张锐尧 肖平 朱忠喜 李军 陈东方 关勤勤

(1.中石化石油机械股份有限公司 2.长江大学石油工程学院 3.中国石油大学(北京)石油工程学院)

0 引 言

深水油气资源储量丰富，勘探开发前景十分广阔。在深水地层中的窄压力窗口以及特有的温度场环境对井筒压力的精确控制提出了挑战，这些工况极易引起溢流、气侵或漏失等井下复杂情况[1-6]。与现有控压钻井技术相比，深水多梯度控压钻井是通过安装在钻柱上的井下分离器短节对钻柱内注入的低密度空心球实现分离且直接注入环空中，以分离器为参考点，能够在环空中形成多个压力梯度，将传统钻井井筒压力的“单一线型”转变成“折线型”，从而可以很好地适应深水地层的窄安全密度窗口，具有广阔的应用前景[7-9]。然而，当钻遇含气储层时，如果压力控制不当，使得井底压力小于地层压力，就会导致气侵或溢流的发生，进一步有可能诱发井涌、井喷等钻井事故[10-16]。因此，为了避免气侵所引发的钻井风险，对气侵后的井底压力实现精确预测显得尤为重要。针对气液相间传质过程的研究，现有模型主要是依据平衡传质理论，即认为气泡会以其固有的溶解度全部进入液相中[17-20]。但是，在气泡从井底向井筒上部运移过程中，气泡表面与液相之间会形成一层传质边界层，而气泡表面存在的表面张力会对气泡进入液相主体中产生传质阻力，即非平衡传质过程。现有气液两相流模型的不足之处是没有考虑气泡的表面张力对传质过程的影响，其气液两相流模型的精度有待进一步提高。

本文在考虑表面张力对传质速率的影响条件下，耦合了井筒温度、压力以及空心球物性参数对井筒流动过程的影响，建立了瞬态非平衡相间传质速率模型，推导了多梯度钻井瞬态传热模型和气液两相流混合水力学模型。最后将上述模型进行耦合，建立了多梯度钻井瞬态非平衡传质两相流新模型，进一步研究了平衡和非平衡条件下对井底处传质速率的影响；同时，在非平衡传质条件下，研究了多梯度钻井关键参数对井底处的传质速率和井底压力的影响。

1 数学模型

1.1 模型假设

气侵后，环空内的气液两相之间会产生相间传质。本文只针对泡状流条件下的井筒传质过程进行研究，并考虑侵入井筒中的自由气体表面张力对相间传质速率的影响。因此，在推导模型前，需要做如下假设：

(1)气液两相不发生边界层分离，且气泡内部可以产生环流；

(2)远离气泡的液相主体为恒定浓度区；

(3)相同截面上，气相与液相的温度相同，且不考虑环境温度对气泡直径的影响；

(4)不考虑岩屑对井筒温度、压力以及流体流动过程的影响。

1.2 非平衡相间传质速率模型

井筒内单个滑移上升气泡与液相之间的非平衡相间传质物理模型如图1所示。本文从井筒中某一截面处的单个气泡的传质过程入手，建立同一截面上的气泡与液相的非平衡传质速率模型。

滑移气泡周围的流场可以用球体绕流方程表示，进一步在球坐标条件下建立绕气泡流动的流函数，计算式为：

(1)

式中：φ为流函数，m3/s；vs为气泡滑移速度，m/s；δ为球坐标系仰角分量，(°)；Ro为距离气泡中心的径向距离，m；rg为气泡半径，m。

液相中的传质扩散方程为：

(2)

式中：vs-r为滑移速度径向分量，m/s；C为气体溶于液体中的气体质量浓度，kg/m3；εg-l为气体分子在液体中扩散系数，m2/s；vs-δ滑移速度的切向分量，m/s。

根据假设条件(2)，远离气泡的液相主体为恒定浓度区域，故气液传质过程主要发生在气液传质边界层中，从而满足如下关系：

(3)

根据式(3)，对式(2)进一步整理，可以得到气泡传质边界层方程：

(4)

于是，根据绕气泡流动的流函数定义，可以得到：

(5)

联立式(1)、式(4)和式(5)，建立气泡界面处质量流量方程：

(6)

式中：Jinf为气液表明边界层的质量流量，kg/s；C1为液相主体中的气体质量浓度，kg/m3；Cinf为气液界面处的质量浓度，kg/m3。

从而得到单个气泡瞬态界面传质速率方程：

(7)

式中：mg-l为气泡表面边界层处的传质质量，kg；t为时间，s；s为气泡表面积，m2。

对式(7)进一步整理，可以得到单个气泡的瞬态传质速率方程：

(8)

由于在同一横截面上存在多个气泡，而气泡间会发生碰撞、变形、聚并和破碎等相互作用，进一步地会增加气液两相之间的传质速率。本文利用FU W.Q.等[21]通过试验数据所拟合的气泡间相互作用系数来体现上述气泡之间的相互作用对传质速率的影响：

(9)

式中：FNb为气泡间相互作用系数；Re为雷诺数；ρg为气体密度，kg/m3；vg为气体运移速度，m/s；Db为管道内径，m；ρL为液相主体的密度，kg/m3；vL为液相的流速，m/s；μg为气体黏度，mPa·s；μL为液相黏度，mPa·s。

从而可以得到整个横截面上的气泡界面传质速率方程：

(10)

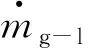
由于现有两相流的气泡界面传质模型中，都是假设两相之间的传质过程为平衡状态，即气相向液相传质过程不需要克服阻力做功，没有考虑气液界面处的张力对传质过程的影响。然而，在气相与液相的交界面处，液相侧浓度与气相侧浓度相差较大，远未达到两相平衡的浓度。所以本文引入非平衡传质理论，得到气液两相交界面处的气体浓度与表面张力之间的关系式为：

(11)

式中：Cb为气液界面处的平衡浓度，kg/m3；p0为大气压，Pa；ρh为混合流体的密度，kg/m3；g为重力加速度，m/s2；χ为溶解度系数，kg/(m3·Pa)；h为气泡所在深度，m；σ为表面张力系数，N/m。

另外，ZHANG R.Y.等[22]通过大量的室内试验，建立了滑移速率与分布系数、特征速度以及气体体积分数之间的关系，该模型已在石油领域广泛使用，具有很好的代表性。本文依据该模型建立了气相的滑移速度模型，其计算式为：

(12)

然后再联立式(9)～式(12)，可以得到滑移气泡的瞬态非平衡传质速率模型：

(13)

式中：Dg为气体分布系数；vc为气体特征速度，m/s；αg为截面含气体积分数，%；K为地层渗透率，μm2；w为泡状流条件下的分布系数；γ为剖面系数递减项；θ为井斜角，(°)。

1.3 多梯度钻井两相流模型

1.3.1 热动力学模型

在深水多梯度钻井中，井下分离器短节将低密度的空心球从钻柱内直接分离后注入环空中，从而对环空中原钻井液的物性参数产生影响。针对环空内的液相，以分离器为参考，上部环空中为低密度空心球与钻井液的混合流体，称为轻质钻井液；下部环空内为原钻井液，称为重质钻井液。下式中式(i)和(ii)分别表示上、下环空中混合流体的热物性参数：

(14)

式中：ρmix为空心球与钻井液混合流体的密度，kg/m3；ρs为空心球的密度，kg/m3；ρm为钻井液密度，kg/m3；ε为注入空心球的体积分数，%；ψ为过滤分离器的分离效率，%；μL为空心球与井液混合液体的黏度，mPa·s；μm为钻井液黏度，mPa·s；μs为空心球黏度，mPa·s。

空心球直径小且密度低，相对于钻井液在井筒内高速流动，其对流动过程产生的影响较小。因此，在考虑空心球对钻井液物性参数影响的条件下，可以将空心球和钻井液的混合流体视为单一的液相。

发生气侵后，环空中气、液两相的热物性参数与温度、压力之间相互影响，且呈动态变化的状态。根据热力学第一定律，建立了深水多梯度钻井条件下的两相流瞬态传热模型：

(15)

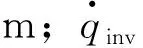
由于钻柱内为单相流体，于是可以依据式(15)，得到钻柱内的传热方程。

钻柱内传热方程如下：

(16)

式中：Dpi为钻柱内径，m；pp为钻柱内液体压力，Pa；Tp为钻柱内混合流体的温度，℃；cL为钻柱内混合流体的比热容，J/(kg·K)；vL为钻柱内混合流体的流速，m/s。

1.3.2 水力学模型

以环空内混合流体的任意单元体为研究对象，考虑气相与液相之间的传质过程，并依据质量守恒和动量守恒原理，建立两相流的混合水力学方程：

(17)

式中：αL为截面液相体积分数，%；αg为截面气相体积分数，%；dw为当量直径，m；p为井筒压力，MPa。

1.3.3 模型离散和求解

对深水多梯度钻井井筒与地层进行网格划分，在径向上采用非均匀网格划分，轴向上使用均匀网格划分。由于多梯度钻井瞬态非平衡传质两相流水力学模型的井筒传热模型以及两相流混合水力学模型都为偏微分方程，具有明显的非线性特点，所以无法通过解析法进行求解。因此本文对温度和压力模型使用隐式有限差分方法进行离散化处理，其中时间导数采用向前差分，一阶空间导数采用向后差分，二阶空间导数使用3点中心差分。基于离散后的差分方程，利用高斯赛德尔循环迭代方法对模型进行求解。

2 敏感性分析

依据表1所示的基础参数，对本文所建立的深水多梯度钻井瞬态非平衡传质的两相流新模型进行数值模拟计算。首先，对比分析了平衡条件和非平衡条件对气液相间传质速率的影响，而传质速率的大小决定了侵入井筒内的自由气体在相同时间内溶解进入液相中含量的高低，从而对井底压力的变化产生直接影响。因此，在非平衡传质条件下，进一步研究了不同多梯度钻井关键参数，如分离器位置与数量、空心球体积分数和密度对井底处的相间传质速率的影响，同时对对应条件下的井底压力随气侵时间的变化进行了模拟，从而可以对多梯度钻井气侵后不同多梯度参数条件下的井底压力动态变化进行预测。

表1 基础参数Table 1 Basic parameters

2.1 平衡与非平衡条件的影响

图2为平衡传质与非平衡传质条件下，井底处相间传质速率和井底压力随时间的变化。由图2a可知：随着循环时间的延长，传质速率先突然增加，然后递增速率逐渐减小。因为当地层中的气体突然侵入井底时，气液两相的边界层处气体浓度突然增加，使得两相之间的体积分数差突然增大，相间传质速率会突然增加；随着侵入气体含量增大，虽然相间体积分数差逐渐增加，但是体积分数差对于传质速率的影响已经达到了极限，相间传质速率继续增加，而递增速率却逐渐减小。与平衡传质相比，因为在非平衡传质过程中，气相与液相之间的传质需要克服界面处的表面张力，其传质过程更困难，对应的相间传质速率更小。

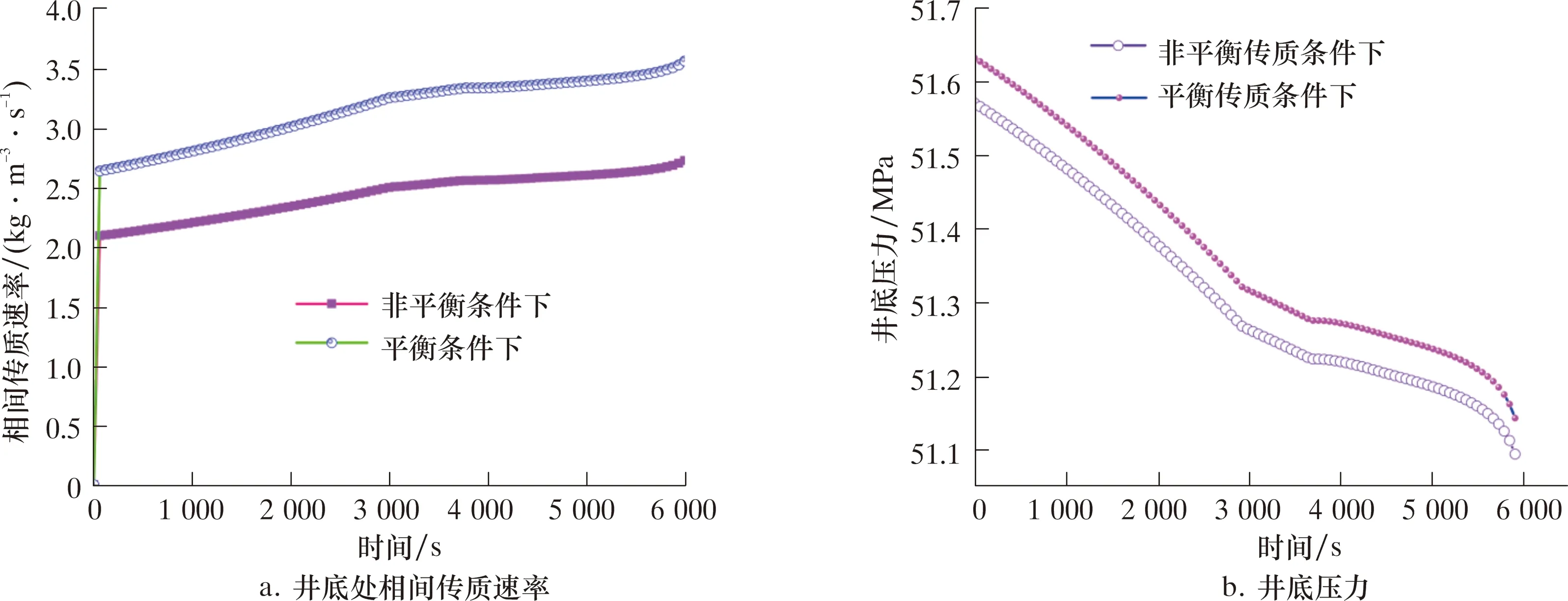
图2 平衡与非平衡条件对井底处的相间传质速率的影响Fig.2 Influence of equilibrium and nonequilibrium conditions on interphase mass transfer at bottom hole

图2b对比计算了平衡和非平衡条件下的井底压力。由上所述，非平衡条件下的气液相间传质速率更小，相同时间内溶解进入液相中的气体含量更低，井筒中自由气体的含量更高，所以井底压力会更低。因为该条件下考虑了气泡表面张力所引起的传质阻力的影响，更符合实际钻井气侵后井筒内气液传质过程，井底压力的预测精度可以提升5.3%。

通过对多梯度钻井气侵后井底压力进行更准确的预测，再结合地层压力的大小，从而可以动态调节多梯度参数对井筒压力进行有效干预。

2.2 空心球体积分数的影响

图3为不同空心球体积分数条件下，井底的相间传质速率和井底压力随时间的变化。

图3 空心球体积分数对井底处的相间传质速率和井底压力的影响Fig.3 Influence of hollow sphere volume fraction on interphase mass transfer rate and pressure at bottom hole

由图3a可以看出，当循环时间相同时，随着空心球体积分数的增加，井底处相间传质速率逐渐降低。因为随着空心球体积分数增加，上部环空中空心球含量增加，轻质流体的密度逐渐减小，而下部环空中重质钻井液的密度保持不变，从而使得井底压力逐渐减小，则气泡直径逐渐增大，导致气液相间界面处的表面张力增大，相间传质速率逐渐减小。随着空心球体积分数的不断增加，一方面使得上部环空内的轻质钻井液的密度不断减小，而下部环空中原钻井液的密度保持不变，从而使得井底压力逐渐减小；另一方面，如上所述，空心球体积分数的增加降低了气液相间传质速率，在相同循环时间内，使得井底处的自由气体的体积分数增加，所以井底压力逐渐降低且递减速率逐渐增加，如图3b所示。

2.3 空心球密度的影响

图4为不同空心球密度条件下，井底处的相间传质速率和井底压力随时间变化的曲线。

图4 不同空心球密度对井底处的相间传质速率和井底压力的影响Fig.4 Influence of hollow sphere density on interphase mass transfer rate and pressure at bottom hole

由图4a可知：由于空心球密度的增加，使得上部环空中的轻质流体的密度增加，下部环空中的重质流体的密度保持不变，所以环空中的静液柱压力逐渐增加，于是井底压力也逐渐增加。从而使得井底处的气泡直径逐渐减小，传质过程需要克服的表面张力也逐渐减小，因此相间传质速率逐渐增加。综上所述，一方面，空心球密度的增加使得环空内的静液柱压力增大，从而导致井底压力逐渐增加；另一方面，空心球密度的增加会使得井底处的相间传质速率逐渐增加，则井底处的自由气体含量逐渐减少，同样也导致井底压力逐渐增加，如图4b所示。但是，空心球密度的变化对井底压力的递减速率影响较小。

2.4 过滤分离器位置的影响

图5为不同过滤分离器位置条件下，井底处的相间传质速率和井底压力随时间变化的曲线。由图5可知，随着过滤分离器位置(距离井口的深度)逐渐增加，在相同循环时间内，井底处的相间传质速率逐渐减小。这是因为随着过滤分离器位置的增加，上部环空中轻质流体的液柱长度增加，而下部环空内的重质流体的液柱长度逐渐减小，所以环空内的静液柱压力逐渐减小，从而导致井底压力逐渐降低。因此，随着井底处的气泡直径逐渐增大，传质过程需要克服的表面张力也逐渐增大，井底处的相间传质速率逐渐降低。由上所述，过滤分离器位置增加，会使得相同井深处的静液柱压力逐渐减小，井底压力逐渐降低；另一方面，过滤分离器深度的增加，使得井底处的相间传质速率逐渐减小，井底处的自由气体的含量增加，从而也会使井底压力减小，如图5b所示。并且，随着过滤分离器位置的增加，井底压力的递减速率逐渐增大。

图5 不同分离器位置对井底处的相间传质速率和井底压力的影响Fig.5 Influence of separator position on interphase mass transfer rate and pressure at bottom hole

2.5 过滤分离器数量的影响

图6为不同过滤分离器数量条件下，井底处的相间传质速率和井底压力随时间的变化曲线。由图6a可知，随着过滤分离器数量的增加，上部环空中轻质流体的液柱长度逐渐增大，下部环空中的重质流体的液柱长度逐渐减小，相同井深处的静液柱压力逐渐降低，导致井底压力逐渐减小。此时井底处的气泡直径逐渐增大，从而使得气液相间传质过程需要克服的表面张力增加，因此井底处的相间传质速率逐渐降低。

图6 不同分离器数量对井底处的相间传质速率和井底压力的影响Fig.6 Influence of separator quantity on interphase mass transfer rate and pressure at bottom hole

由图6b可知：过滤分离器数量的增加，一方面使得环空内的静液柱压力逐渐降低，井底压力逐渐减小；另一方面，其降低了井底处的相间传质速率，使得井底处的自由气体含量增加，从而也会进一步导致井底压力降低。并且，随着过滤分离器数量的增加，井底压力的递减速率也会逐渐增大。

3 结 论

本文基于非平衡界面传质理论，推导了瞬态气液相间传质速率模型，考虑井筒与地层间能量交换以及空心球物性参数对井筒气液两相流的影响，进一步建立了深水多梯度钻井瞬态非平衡传质两相流新模型。最后对模型进行了求解和敏感性分析，并得到如下结论：

(1)与现有模型计算结果相比，非平衡相间传质速率模型考虑了气泡表面张力所引起的传质阻力对相间传质速率的影响，因此其相间传质速率更小，相同时间内在该条件下井筒内的自由气体所溶解的含量更低，自由气体的含量更高，井底压力更低，井底压力的预测精度可以提升5.3%。

(2)所建立的深水多梯度钻井瞬态非平衡传质两相流新模型，可以更准确地预测多梯度钻井条件下井底压力随气侵时间的动态变化，从而为进一步地调节多梯度参数进行井筒压力控制提供参考。该模型适用于深水钻井条件，如果不考虑空心球的影响，也可以适用于常规钻井方法。

(3)在非平衡传质条件下，井底压力与分离器位置、数量或空心球体积分数的变化呈负相关，随着上述参数的增大，其递减速率逐渐增加；随着空心球密度的增加，井底压力逐渐升高，但是其递减速率变化不大。