多策略增强型麻雀搜索算法

陈建东　聂斌　雷银香　张玉超　陈星鑫　苗震

摘  要：为进一步提升麻雀搜索算法（SSA）的收敛速度和求解精度，并且针对麻雀种群的全局搜索能力较弱和在迭代后期易陷入局部最优的问题，提出一种多策略增强型的麻雀搜索算法（MESSA）。首先，采用Bernoulli映射初始化种群，保证种群的多样性和均匀性，提升算法的收敛速度。其次，引入Levy飞行来增强麻雀种群中个体发现者的全局搜索能力。然后，引入交叉优化算法，帮助麻雀种群陷入停滞时摆脱停滞状态，跳出局部最优的同时提升求解精度。通过9个基准函数实验证明MESSA能提升SSA的性能。

关键词：麻雀搜索算法；Bernoulli映射；Levy飞行；交叉优化算法；特征选择

中图分类号：TP18  文献标识码：A      文章编号：2096-4706（2023）13-0039-08

Multi-Strategy Enhanced Sparrow Search Algorithm

CHEN Jiandong， NIE Bin， LEI Yinxiang， ZHANG Yuchao， CHEN Xingxin， MIAO Zhen

（College of Computer Science， Jiangxi University of Chinese Medicine， Nanchang  330004， China）

Abstract： A Multi-Strategy Enhanced Sparrow Search Algorithm （MESSA） is proposed to further improve the convergence speed and solution accuracy of the Sparrow Search Algorithm （SSA）， as well as to address the problems of the sparrow population's weak global search ability and the tendency to fall into local optimum in the late iteration. Firstly， Bernoulli mapping is used to establish the population in order to ensure population diversity and homogeneity while also increasing the algorithm's convergence speed. Secondly， Levy flight is introduced to improve individual discoverers' global search ability in the sparrow population. Then， the Crossover Optimization Algorithm is introduced to assist the sparrow population in breaking free from the stagnation stage， jumping out of the local optimal， and boosting solving accuracy. Nine benchmark function experiments demonstrate that MESSA can improve the performance of SSA.

Keywords： Sparrow Search Algorithm; Bernoulli mapping; Levy flight; Crossover Optimization Algorithm; feature selection

0  引  言

麻雀搜索算法（Sparrow Search Algorithm， SSA）是由薛建凯等[1]在2020年提出的新型群体智能算法，灵感来源于麻雀的觅食行为和反觅食行为。麻雀搜索算法具备结构简单、控制参数少、求解精度高等优点。李雅丽等[2]通过对比实验证明麻雀搜索算法的稳定性和收敛精度领先于其他五种新型智能算法。因此，作为一种有潜力的优化算法，SSA已经被广泛应用到各个研究领域中。Yuan等[3]针对光伏微电网系统局部阴影下功率失配损失的问题，提出一种基于改进麻雀搜索算法（ISSA）的分布式最大功率点跟踪方法，能更准确、更快速地跟蹤最大功率点，具有良好的稳态性能。Liu等[4]提出了一种改进的麻雀搜索算法 CASSA 来建立3d任务空间模型和无人机路径规划成本函数，将路径规划问题转化为多维函数优化问题，实验证明在考虑各种约束条件下能更有效地解决无人机路线规划问题。Zhu等[5]提出了一种称为自适应麻雀搜索算法（ASSA）的新优化算法，用于质子交换膜燃料电池（PEMFC）电堆的最佳模型参数识别，实验证明所提出的ASSA具有最佳效率。

与大多数智能优化算法相比，SSA在问题优化方面有一定优势，但是，依然存在寻优精度较低，在搜索接近全局最优时，存在种群的多样性减少，容易陷入局部最优等问题。针对这些问题，许多学者提出了改进策略。李爱莲等[6]提出了一种融合正余弦和柯西变异的麻雀搜索算法，实验结果证明改进后的SSA在收敛速度和寻优精度有明显增强，表现出良好的鲁棒性。Cheng等[7]提出了一种学习麻雀搜索算法，在CEC2017测试函数和基准函数上取得了良好的效果，在一定程度上避免了算法陷入局部最优的问题。Yan等[8]提出一种基于迭代局部搜索的改进麻雀搜索算法，在基准测试函数和 CEC2017函数上的实验表明，该算法提升了搜索精度，并且在算法陷入局部最优时有跳出局部最优的能力。

虽然上述学者都对SSA提出了改进，但SSA仍然存在易陷入局部最优和寻优精度不高的问题。因此，本文通过引入Bernoulli映射、Levy飞行策略和交叉优化算法对SSA进行改进，提出一种融合多策略的增强型麻雀搜索算法（Multi-strategy enhanced sparrow search algorithm， MESSA），提升SSA性能的同时增强SSA跳出局部最优的能力。

1  麻雀搜索算法概述

麻雀搜索算法主要模拟了麻雀群体觅食的过程，麻雀们在觅食的过程中有三种行为策略：发现者、跟随者和警戒者。其中适应度较高的麻雀作为发现者，负责搜索食物，10%～20%的个体被随机分配为跟随者，跟随发现者获取食物，警戒者对环境威胁保持警惕并警告麻雀种群向安全区域靠近。麻雀搜索算法的主要步骤如下：

1）初始化麻雀种群位置。由n只麻雀种群的初始位置在d维解空间内表达如式（1）所示：

其中，n表示麻雀个体数量，n表示待优化问题的变量维度。通过该矩阵可求出初始种群的适应度值如式（2）所示。

其中，F表示适应度值，f表示求取适应度值的函数。

2）种群中发现者负责寻找食物的方向和位置，并带领跟随者向食物方向靠近。种群中发现者位置更新如下：

其中t表示当前迭代次数，tmax表示最大迭代次数，ST是预设的安全阈值，R2表示预警值。 表示第i个麻雀在第j维的个体位置。α ∈（0，1）是一个随机数。Q表示服从正态分布的随机数。当R2＜ST时，这表明此时种群环境是安全的，周围没有发现捕食者，发现者可以进行广泛的搜索，当R2≥ST时，表示群内个体已发现捕食者并发出警报，群内所有个体将进行反捕食行动，发现者将引导追随者至安全位置。

3）为了获得优质的食物，跟随者追随发现者或独自觅食，跟随者的位置更新如式（4）所示：

其中， 表示第t + 1代跟随者所处最佳位置， 表示当前适应度最差的位置，A表示一个1×d维的矩阵，这个矩阵中每个元素随机赋值为1或-1，其中 。当i＞n/2时，这表明适应性较差的第i个跟随者没有得到食物，非常饥饿，需要飞到别处获取更多能量；当i≤n/2时，追随者监视发现者并与更高的捕食者竞争食物，从而增加他们的能量。

4）警戒者是在种群中随机选择的个体。当感知到危险时，它们会发出信号让麻雀逃到安全的位置。警戒者的位置更新公式如式（5）所示：

式（5）中， 表示当前全局最优值，α为控制步长参数，服从标准正态分布，β表示-1和1之间的随机数，fi表示当前麻雀的适应度值，fg和fw分别表示当前搜索范围内的最佳和最差适应度值，ε是防止分母为0的最小实数。当fi ≠ fg时，表示麻雀是处于种群边界，容易受到捕食者的攻击，因此需要调整位置。当fi = fg时，这表明种群中的麻雀个体意识到了危险，需要靠近其他麻雀以避免危险。

2  融合多种策略的增强型麻雀搜索算法

2.1  Bernoulli映射

Kazimipour等人[9]指出一个好的初始种群会影响着演化算法寻找全局最优的进程，如加速种群收敛，提高最终解的精度。现有的种群初始化技术主要分为随机性、组合性和通用性这三类。而大多数群体智能算法都采用随机性算法生成初始种群。

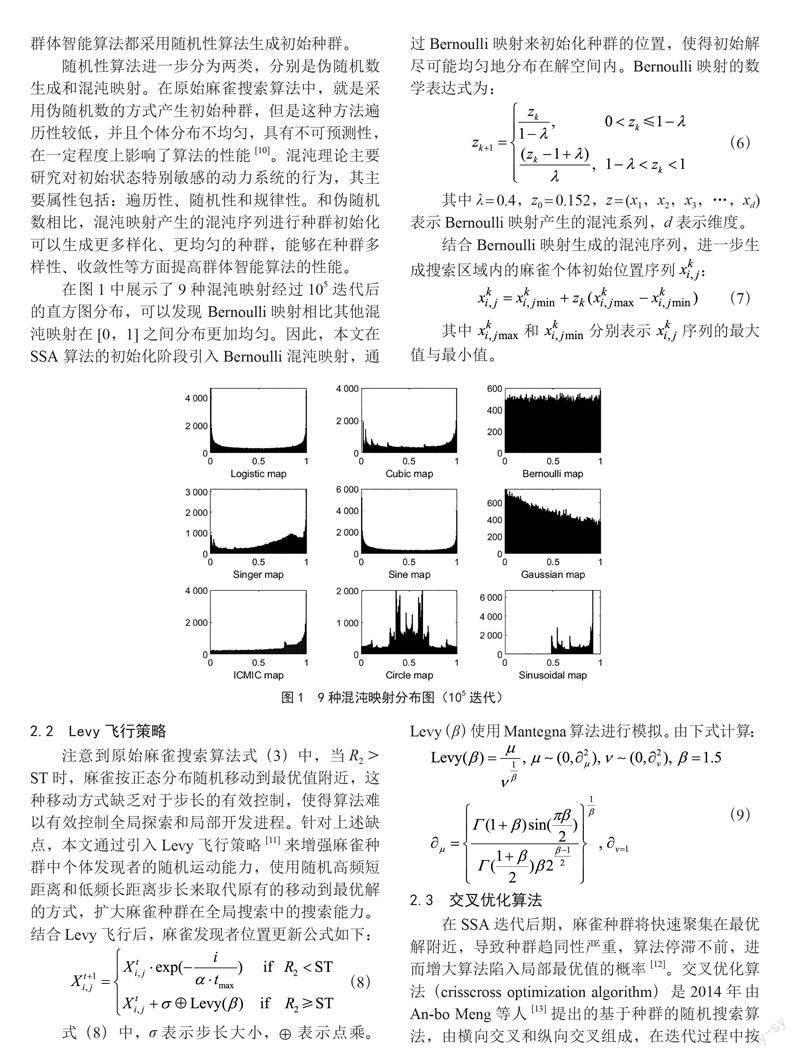
随机性算法进一步分为两类，分别是伪随机数生成和混沌映射。在原始麻雀搜索算法中，就是采用伪随机数的方式产生初始种群，但是这种方法遍历性较低，并且个体分布不均匀，具有不可预测性，在一定程度上影响了算法的性能[10]。混沌理论主要研究对初始状态特别敏感的动力系统的行为，其主要属性包括：遍历性、随机性和规律性。和伪随机数相比，混沌映射产生的混沌序列进行种群初始化可以生成更多样化、更均匀的种群，能够在种群多样性、收敛性等方面提高群体智能算法的性能。

在图1中展示了9种混沌映射经过105迭代后的直方图分布，可以发现 Bernoulli映射相比其他混沌映射在[0，1]之间分布更加均匀。因此，本文在SSA 算法的初始化阶段引入Bernoulli混沌映射，通过Bernoulli映射来初始化种群的位置，使得初始解尽可能均匀地分布在解空间内。Bernoulli映射的数学表达式为：

其中λ = 0.4，z0 = 0.152，z = （x1，x2，x3，…，xd）表示Bernoulli映射产生的混沌系列，d表示维度。

结合Bernoulli映射生成的混沌序列，进一步生成搜索区域内的麻雀个体初始位置序列 ：

其中  和  分别表示  序列的最大值与最小值。

2.2  Levy飞行策略

注意到原始麻雀搜索算法式（3）中，当R2＞ST时，麻雀按正态分布随机移动到最优值附近，这种移动方式缺乏对于步长的有效控制，使得算法难以有效控制全局探索和局部开发进程。针对上述缺点，本文通过引入Levy飞行策略[11]来增强麻雀种群中个体发现者的随机运动能力，使用随机高频短距离和低频长距离步长来取代原有的移动到最优解的方式，扩大麻雀种群在全局搜索中的搜索能力。结合Levy飞行后，麻雀发现者位置更新公式如下：

式（8）中，σ表示步长大小， 表示点乘。Levy（β）使用Mantegna算法进行模拟。由下式计算：

2.3  交叉优化算法

在SSA迭代后期，麻雀种群将快速聚集在最优解附近，导致种群趋同性严重，算法停滞不前，进而增大算法陷入局部最优值的概率[12]。交叉优化算法（crisscross optimization algorithm）是2014年由An-bo Meng等人[13]提出的基于种群的随机搜索算法，由横向交叉和纵向交叉组成，在迭代过程中按顺序执行。CSO中的横向交叉以一定的概率搜索每个超立方体的外围，其次，引入纵向交叉的动机是为了在种群陷入停滞时摆脱停滞状态。一旦个体的某个停滯维度在纵向交叉操作中跳出局部最小值，它将通过横向交叉迅速传播到整个群体。这反过来又有助于其他停滞维度在纵向交叉操作中尽快跳出局部最小值。因此，为进一步增强麻雀搜索算法跳出局部最优的能力，提升求解精度，本文引入交叉优化算法。下面将对横向交叉和纵向交叉进行介绍。

2.3.1  横向交叉

横向交叉是对群体中的两个不同个体在相同维度上的算术交叉，在本文中，第i个警戒者麻雀父体  和第j个警戒者麻雀父体  在第d维上进行横向交叉，它们的后代将由下式计算：

式（10）中，m1和m2是在[0，1]之间按照均匀分布随机生成的值，n1和n2是[-1，1]之间按照均匀分布随机生成的值。 和  分别是  和  的第d维。 和  分别是  和 在第d维交叉后产生的后代。产生的后代将与父代进行竞争，最终保留适应度更高的麻雀个体。

2.3.2  纵向交叉

纵向交叉是在两个不同维度之间对个体进行的算术交叉，需要注意的是，此时纵向交叉搜索的父种群是来自横向交叉后更优的种群。由于个体解的每个维度可能具有不同的上界和下界，因此需要根据每个维度的上界和下界进行归一化操作，以确保纵向交叉产生的后代能够位于每个维度的边界内，并且纵向交叉每次只对其中一维进行更新既能够使陷入局部最优的维度跳出局部最优，而又尽可能不破坏另一正常维度包含的信息。假设横向交叉后更优的麻雀个体为 ，此时对  的第d1维和d2维进行纵向交叉，它们的后代将由下式计算：

式（10）中，m是[0，1]之间按照均匀分布随机生成的值， 为父代  的第d1维和第d2维通过纵向交叉产生的后代。同横向交叉的竞争机制一样，最终保留适应度更高的麻雀个体。

2.4  MESSA的算法步骤

融合多种策略之后的增强型麻雀搜索算法（Multi-strategy enhanced sparrow search algorithm， MESSA）的具体实现步骤为：

1）算法相关参数初始化，设定种群规模pop，最大迭代次数tmax，搜索范围上下界ub，lb。预警值ST，发现者的比例PD，警戒者的比重SD。

2）根据式（6）初始化种群

3）计算初始适应度值并进行排序找到当前最优适应度值，记录此时的最优位置和最差位置。

4）在PD中选取适应度较高的麻雀个体通过式（8）更新发现者位置，剩下的作为跟随者通过式式（4）更新位置。

5）在SD中根据式（5）更新麻雀位置

6）随机选取麻雀个体通过式（10）进行横向交叉，保留此时适应度更高的麻雀个体 ，横向交叉结束后，根据式（11）进行纵向交叉，更新当前最优麻雀个体。

7）比较纵向交叉后的麻雀个体适应度值，得出全局最优解。记录当前麻雀个体位置。

8）判断当前迭代次数是否达到设置的tmax，若达到则输出最优麻雀个体适应度值和最优麻雀个体位置，否则返回3）。

3  MESSA实验与讨论

3.1  实验设计

为了综合验证MESSA的有效性，实验选取已发表文献中的9个基准测试函数测试MESSA的性能，并与原始麻雀搜索算法SSA、李爱莲等提出的融合正余弦和柯西变异的麻雀搜索算法（Sine-cosine and cauchy mutation sparrow search algorithm， SCSSA）、经典优化算法PSO和GWO进行对比。基准测试函数的相关信息如表1所示。包括：单模态测试函数F1～F3，只有一个全局最优解，主要用于测试算法的寻优精度；多模态测试函数F4～F6，具有多个局部最优解，用于检验算法的全局搜索性能和避免早熟的能力；固定維度复合测试函数F7～F9，这些函数的特点是维度比较低，只有一个全局最优解的同时，还有许多局部最优解，要求算法在优化低维问题具有一定的能力。其中F1～F6分别在10维、30维和100维中运行，每个算法均独立运行100次，验证MESSA在不同维度下的求解能力。实验结果如表3和表4所示，在F7～F9中运行固定维度的测试结果如表1所示，实验采用最优值（Best）、平均值（Mean）和标准差（Std）来评估MESSA的性能，其中最优值和平均值反映算法的求解质量和求解精度，标准差反映算法的稳定性。为了展示不同算法的收敛性能，绘制了不同算法在30维的收敛曲线图，如图5所示，其中纵坐标代表适应度值以10为底的对数。

本节所有实验仿真测试环境为AMD R7-5800H、3.4 GHz CPU、16 GB RAM和Windows 11（64 位）操作系统，所有算法实验均在Matlab R2021a上运行。

3.2  实验结果与分析

由表2、表3和表4可知：

1）在函数F1～F3上，SCSSA和MESSA在维度为10维、30维、100维均取得了函数理论最优值，并且在平均值和标准差上都最优。

2）在函数F4上，SSA、BSSA、LSSA、CSSA、SCSSA和MESSA在10维、30维和100维都取得了近似最优结果，其中SCSSA和MESSA在平均值和标准差上都有着最佳的表现，SSA在30维时相比其他五个算法在平均值和标准差上略微逊色，但依旧好于GWO和PSO。

3）在函数F5，F6上，在维度为10维、30维和100维时，MESSA在三个指标上相比其他算法均有着更优的表现，且远优于SSA和SCSSA。

4）在F7和F8上，MESSA在三个指标上相比其他算法均有着更优的表现。在函数F9上，除了SSA和SCSSA，其余算法均取得了函数理论最优值，GWO、PSO在平均值上均取得了最优结果，PSO在标准差上取得了最优结果。

由图2可知，在a～h的图像中可以发现，随着迭代次数的增加，MESSA相比其他算法收敛速度更快，并且在相同迭代次数的情况下有着更高的精度。其中在图2（g）中，其他算法都陷入了局部最优，只有MESSA收敛于全局最优，表明MESSA有着更强的跳出局部最优的能力。虽然在图2（i）中CSSA收敛更快，但MESSA达到了次优，依然领先SSA和SCSSA。

因此，综合上述分析，融合三种改进策略的MESSA相比其他算法在三个评价指标上表现更好，说明三种策略之间的融合能最大程度地提升算法的性能，说明了改进策略的可行性。这是因为MESSA通过Bernoulli映射使得麻雀种群更加均匀，保证了种群的多样性，提升了算法的收敛速度和寻优精度。而引入莱维飞行后MESSA搜索范围变得更大，提升了算法的寻优精度，同时交叉优化算法中的交叉算子大大提高了SSA跳出局部最优的能力。表明多种策略的融合能进一步提升SSA的性能，改进是有效的。

4  结  论

本文通过对SSA的分析，针对其不足之处提出一种融合多种策略的增强型麻雀搜索算法（MESSA），在9个基准测试函数上的实验验证了MESSA的性能。在接下来的研究中，将尝试使用本文提出的MESSA更多地应用到工程优化问题和特征选择问题中。

参考文献：

[1] XUE J K，SHEN B.A novel swarm intelligence optimization approach：sparrow search algorithm [J].Systems Science & Control Engineering，2020，8（1）：22-34.

[2] 李雅丽，王淑琴，陈倩茹，等.若干新型群智能优化算法的对比研究 [J].计算机工程与应用，2020，56（22）：1-12.

[3] YUAN J，ZHAO Z，LIU Y，et al. DMPPT control of photovoltaic microgrid based on improved sparrow search algorithm[J]. IEEE Access，2021，9：16623-16629.

[4] LIU G，SHU C，LIANG Z，et al. A modified sparrow search algorithm with application in 3d route planning for UAV [J].Sensors，2021，21（4）：1224.

[5] ZHU Y，YOUSEFI N. Optimal parameter identification of PEMFC stacks using adaptive sparrow search algorithm [J].International journal of hydrogen energy，2021，46（14）：9541-9552.

[6] 李爱莲，全凌翔，崔桂梅，等.融合正余弦和柯西变异的麻雀搜索算法 [J].计算机工程与应用，2022，58（3）：91-99.

[7] OUYANG C，ZHU D，WANG F. A learning sparrow search algorithm [J].Computational intelligence and neuroscience，2021，2021：1-17.

[8] YAN S，YANG P，ZHU D，et al. Improved Sparrow Search Algorithm Based on Iterative Local Search[J/OL].Computational Intelligence and Neuroscience，2021，2021：（2021-12-15）.https：//doi.org/10.1155/2021/6860503.

[9] KAZIMIPOUR B，LI X，QIN A K. A review of population initialization techniques for evolutionary algorithms [C]//2014 IEEE congress on evolutionary computation （CEC）.New York：IEEE，2014：2585-2592.

[10] 段玉先，劉昌云.基于Sobol序列和纵横交叉策略的麻雀搜索算法 [J].计算机应用，2022，42（1）：36-43.

[11] 王庆喜，郭晓波.基于莱维飞行的粒子群优化算法 [J].计算机应用研究，2016，33（9）：2588-2591.

[12] 张琳，汪廷华，周慧颖.一种多策略改进的麻雀搜索算法 [J].计算机工程与应用，2022，58（11）：133-140.

[13] MENG A，CHEN Y，YIN H，et al. Crisscross optimization algorithm and its application [J].Knowledge-Based Systems，2014，67：218-229.

作者简介：陈建东（1997—），男，汉族，江西赣州人，硕士研究生，研究方向：数据挖掘；通讯作者：聂斌（1972—），男，汉族，江西吉安人，教授，硕导，CCF会员，研究方向：数据挖掘;雷银香（1989—），女，汉族，江西井冈山人，硕士，讲师，研究方向：信息安全；张玉超（1998—），男，汉族，重庆人，硕士研究生，研究方向：数据挖掘；陈星鑫（1999—），男，汉族，江西赣州人，硕士研究生，研究方向：数据挖掘；苗震（1997—），男，汉族，吉林辽源人，硕士研究生，研究方向：数据挖掘。

收稿日期：2023-02-15

基金项目：江西中医药大学星火传承培养计划（2252000111/4004）；江西省教育厅科学技术项目（GJJ2200925）；江西省中医药管理局科技计划项目（2020B0412）；江西中医药大学校级科技创新团队发展计划（CXTD22015）