基于5G 终端的室内3D 定位*
咸立文,张小琼,吴晓晟,刘 旭
(1.中国电子科技集团公司第三十研究所,四川 成都 610041;2.武警重庆总队参谋部,重庆 401147)
0 引言
目前,基于位置的服务(Location Based Service,LBS)已经迅速发展并广泛应用于室外环境。利用卫星导航技术,室外定位应用如行车导航和紧急救援等已经达到了较高的技术成熟度和产业化水平。然而,随着经济社会的发展及智能家居、智能医疗等场景的兴起,定位技术的需求逐渐扩展到室内领域。由于室内环境的复杂性和多径衰落等影响因素的存在,卫星信号很难满足人们对室内位置信息的准确需求。因此,出现了多种室内定位技术,如基于接收信号强度指示(Received Signal Strength Indicator,RSSI)[1-2]、飞行时间(Time of Flight,ToF)[3-4]、到达时间差(Time Difference of Arrival,TDoA)[5-6]、往返时间(Round-Trip Time,RTT)[7]、到达角度(Angle of Arrival,AoA)[8-9]、指纹等的定位技术。
基于RSSI 的定位方式通过建立电磁波衰减模型来计算收发机之间的距离,并利用多个基站构建多站定位模型。该定位技术的优点在于实现简单,算法复杂度低,且不需要严格的时间同步。然而,它容易受到多径环境的影响,在室内复杂的无线环境下,其定位效果不理想。基于ToF 的定位技术是通过计算信号在无线环境中传播的时间来估算收发机之间的距离。该定位模型结构简单,但实现难度较大,因为需要收发机之间的时间严格同步,并且信号传播过程中的折射、反射等误差会导致距离计算中的误差。基于TDoA 的定位技术利用信号的到达时间差作为基本观测量。相比基于ToF 的方法,它避免了对收发机时间同步的需求,降低了工程实现的难度。然而,在该方法中,无线信号传播中存在的误差仍会影响定位精度。基于RTT 的定位技术类似于雷达测距,通过测量信号的往返时间来计算传播距离。这种方法要求接收端快速响应,定位精度会受到系统响应时间的影响。基于AoA 的定位方法利用天线阵列分辨信号达到的角度,并利用多个基站进行联合定位。该方法的优势在于精度高、所需基站数量较少且无须时钟同步。然而,该方法信号解算的复杂度较高,难以适用于高并发、大容量的场景。基于RSSI 指纹的定位技术是基于RSSI 定位技术的升级,通过提前采集信号并构建指纹库来实现定位。相比于传统的RSSI 定位技术,该方法具有更高的定位精度。然而,由于任何无线环境的改变都需要重新收集指纹,导致系统的部署和应用相对困难。
随着室内定位技术的发展,现有的定位系统通常采用多种技术的融合以提高精度。然而,当前的室内定位领域仍存在一些问题。首先,许多先进的定位系统是基于服务器端而非终端设备,存在信息泄露风险,并且难以支持高并发和大容量场景。其次,大多数定位系统只能在二维平面上进行定位,而随着基于位置服务的应用需求增加,对于3D 定位的需求也日益增多。例如,在智能家居和养老院等场景中,需要对孩子和老人进行安全监护;在大型商超的导航和智慧仓储等场景中,需要对物品进行单站的3D 定位。此外,基于射频识别技术(Radio Frequency Identification,RFID)、蓝牙、超宽带(Ultra Wide Band,UWB)等系统的定位技术需要额外的硬件设备,增加了部署成本。
为了解决上述问题,本文提出了一种基于5G终端的3D 定位技术,充分利用了5G 基站的普及和5G 基站天线阵列的优势。本文提出的技术利用正交匹配追踪算法(Orthogonal Matching Pursuit,OMP)[10]在5G 终端上计算基站发出信号的离开方位角和离开仰角。随后,通过提出的直射路径识别算法,确定来自两个基站的三维路径,并利用两个基站的三维直射路径和TDoA 构建定位模型,从而获得终端的位置信息。考虑到在3D 空间中两条射线不一定会有确定的交点,本文引入基于遗传算法(Genetic Algorithm,GA)[11]的目标位置搜索算法,以优化求解。
本文的最主要贡献包括:
(1)所提出的技术基于5G 终端进行定位,有效避免了隐私泄露的风险。通过在终端设备上解算角度信息,可以减少基站端的并发处理,从而减轻系统的负担。此外,由于与通信网络的一体化,该技术还能够降低系统的部署成本。
(2)本文提出了一种联合定位模型,利用离开方位角、离开仰角和到达时间差等多个参数进行定位。同时,引入直射路径识别算法来确定基站到终端的直射路径。此外,为了优化求解,本文还提出了基于遗传算法的智能搜索算法,用于获取目标位置的更准确解。
(3)本文使用MATLAB 进行了仿真实验,以具有4 天线组成面阵天线阵列的5G 基站为例,构建了信号传播模型,并进行了定位测试。仿真结果显示,所提出的定位技术可以实现1.12 m 的3D 定位精度,验证了该技术的有效性。
1 基于5G 终端的室内3D 定位
本文提出的系统的流程如图1 所示。该系统利用两个已知位置的5G 基站,每个基站都由4 个天线组成的均匀面阵阵列发送射频信号。终端接收信号,并使用超分辨算法计算出射频信号的离开方位角和离开仰角。然后,利用这些角度信息建立几何定位模型,并结合TDoA进行约束,以确定目标位置。最后,提出了基于遗传算法的目标位置搜索算法,用于求解目标位置。下面详细介绍定位过程。

图1 定位流程
(1)角度估计。首先建立基站与终端的通信连接并测量基站的来波信号,利用OMP 估计来波二维角度。
(2)直射路径识别。利用提出的直射路径识别算法对信号进行分析,以确定是否存在直射路径。该算法能够识别出信号传播过程中的直射路径,从而帮助准确定位目标。
(3)目标定位。使用两个基站的直射路径构建3D 定位模型,利用两个基站的TDoA 约束目标位置,最后使用所提的基于GA 的智能搜索算法在3D 空间中对目标位置进行优化求解目标位置。
1.1 二维离开角估计
图2 展示了均匀面阵阵列模型。5G 基站所发射信号为正交频分复用调制,且是窄带信号。假设符合远场条件,基站的天线数量为R=2×2,阵列的间距为m=λ/2,λ为波长。终端接收到第r个发射天线的信号可以表示为:
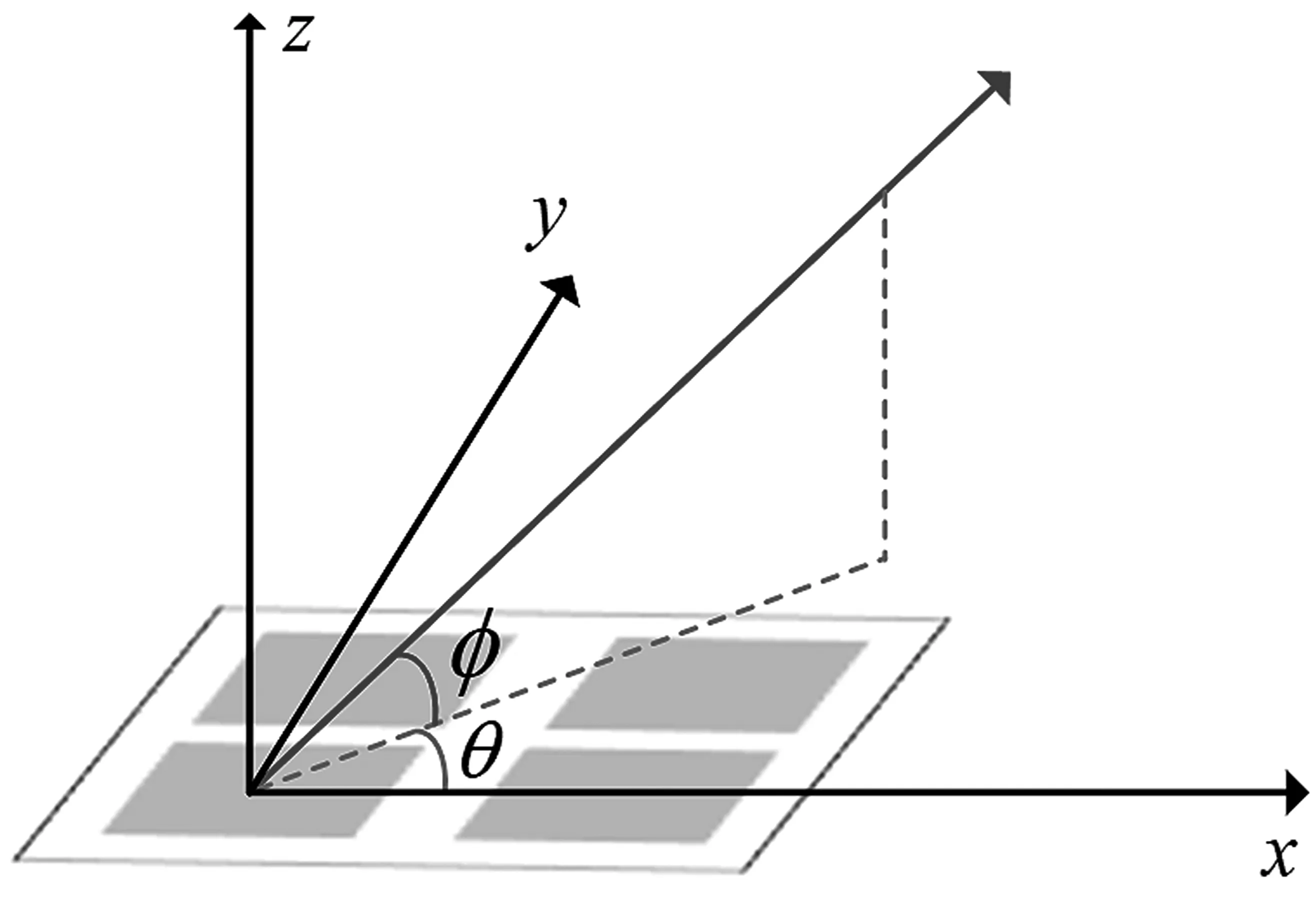
图2 天线阵列
式中:xr(t)为接收端收到的第r个发射天线的信号;ar和τr分别为从基站第r个发射天线到用户终端的衰减和传播延迟;nr(t)是第r个天线的加性高斯白噪声。根据图2,发射阵列天线与原点处天线的x轴、y轴和z轴上的距离差可以表示为:
另外,发射信号可以表示为:
假设传输过程中有I条多径,则式(4)可以表示为:
本文使用OMP 算法进行二维离开角度估计。OMP 算法是MP 的扩展,其改进的核心是对选定的原子进行正交化,这使得算法在相同的精度下收敛更加迅速。并且通过原子之间的正交,算法对多径弱信号的提取会更加理想。在参数估计时,由于在典型的室内环境中,通常存在5~6 条多径数量,也正好满足了OMP 算法要求的稀疏性。因此,式(5)与式(6)的解就可以转化成以下非线性约束问题:
式中:ε为正则式参数;为实际路径的真实参数;是一个完备的字典矩阵。可以表示为:
式中:N由AoA、EoA 及ToF 的搜索范围和搜索步长决定,其中每一个被称为中的一个原子。OMP 算法主要有以下几个步骤:
(1)设置残差v0=X,索引集0=∅Γ,原子向量0=∅Λ,稀疏度E=L和迭代次数j=1。
(2)更新索引集和原子集,其更新的公式为:
(4)更新残差vj,可以表示为:
(5)如果当j>E,就停止算法迭代。否则返回步骤(2)再次循环。
在上述OMP 算法中,通常E为室内路径的数量,其可以参考典型室内的路径数量设置为5~6条,也可以通过对信号进行奇异值分解获得。在本文中将信号路径数量固定为6 条。当算法循环完成后,则可以获得一个信道状态信息(Channel State Information,CSI)包中多径信号的离开方位角和离开仰角等参数的估计值。
1.2 直射路径识别算法
完成对路径的参数估计以后,考虑定位模型是利用双基站的直射路径构建,那么需要在多路径中识别和提取直射路径,以满足定位模型的要求。通常,在基于ToF 的定位系统中,可以使用最短的ToF 来确定直射路径。但绝对ToF 的估计需要收发设备之间严格的时间同步,本文所提算法为了使系统简单、易部署,没有估计ToF。因此,不能将信号的最短ToF 作为选择直射路径的判断条件。
为了获得信号传播的直射路径,本文提出了基于多包聚类和仿射传播算法的直射路径识别算法。该算法基于以下原理:在视距环境中,直射路径相对于反射路径更为稳定。通过多个包的聚类,直射路径对应的簇在角度域上表现出较小的抖动,表现为参数的方差较小且极值点较多且集中。相反,反射路径在角度域上的表现与直射路径相反,因为信号的反射是随机且不稳定的,反射路径会表现出较大的波动和不稳定性,这些特征可以通过角度域的参数来体现。因此,通过多包聚类后,直射路径的参数的方差会较大,而每个簇的极值点数量也较少。基于以上讨论,可以通过路径在空域、极值点数量及各簇的方差等特征来判别直射路径和反射路径。同时,在进行多包聚类后,可以提取每个簇的平均值作为路径的离开方位角和离开仰角,以减少参数估计误差。在本文中,首先对单独的10 个数据包进行参数估计,其次对这10 个数据包的参数估计结果进行聚类。在聚类的基础上,本文扩展了SpotFi[12]系统中基于最大似然打分的方法,将离开仰角作为核心的判别依据。其中,任意一条传播路径的得分可以表示为:
式中:n,σθ和σϕ分别为传播路径对应的簇的极值点个数、离开方位角的方差和离开仰角的方差;wc,wθ和wϕ分别为对应分配给路径的数量、离开仰角的方差和离开方位角的方差的权重值,为常数,由大量实验的统计结果得出。在此基础上,求取每一簇极值点的离开方位角、离开仰角的平均值作为该簇对应路径最后的离开方位角、离开仰角,以减少使用单个包估计存在的随机误差。最终输出所有簇对应路径的离开方位角、离开仰角、对应路径获得的分数(置信度)和直射路径与反射路径的判定结果,其中分数最高的为直射路径,其余为反射 路径。
1.3 目标定位
由于通过参数估计得到的直射路径参数带有误差,而在3D 空间中两条带有误差的射线不一定存在交点,本文所提定位模型很难得到目标的确定解。因此,为了获得目标位置,提出基于GA 的目标位置搜索算法。GA 是一种模拟在自然环境中的生物遗传和进化的过程而形成的自适应全局搜索算法。GA 是一种高效、鲁棒性强的优化算法,算法形成的过程中借鉴了生物界遗传学说和进化论的相关知识,分别被称为交叉运算和变异运算,算法在解空间搜索的过程中会自动获取和累计与解空间相关的知识,然后适应性地控制搜索过程并获得最优解。
定位模型如图1 所示,为了描述方便,采用了笛卡尔坐标对目标以及基站的位置进行简化描述。其中,基站1 和基站2 的位置已知,分别表示为B1=[x1,y1,z1]T和B2=[x2,y2,z2]T,目标的位置未知,表示为t=[x,y,z]T。为了开始GA,需要给定一定数量的个体,也称染色体,即目标解,每个个体由基因构成,所有的个体被称为群体。对应在当前算法中,每一个目标解被称为一个染色体,目标解的构成元素则被称为基因。为了使算法更快地收敛,两个基站的TDoA 被用来约束算法的搜索范围,即目标解空间,考虑到TDoA 受室内环境的影响,因此TDoA 只用来约束解空间的范围,提高算法的收敛速度,算法以角度作为核心判断条件。然后,目标区域可以通过这个范围和两个基站的直射路径角度来大致确定。如图3 所示,为了在这个粗略的区域内精确找到目标位置,有以下关键步骤:
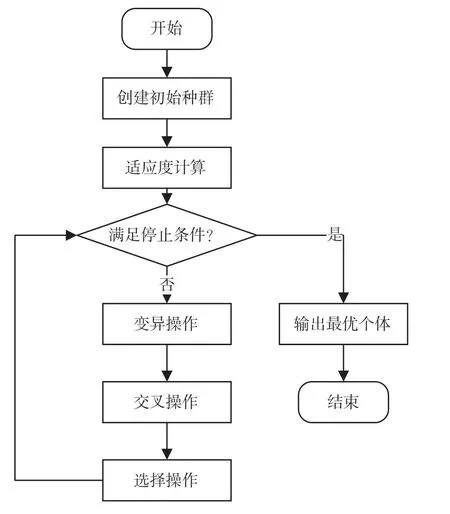
图3 算法流程
(1)设置群体数量为N,并初始化初始群体,表示为T=[t1,…,tN],其中个体表示为ti=[xi,yi,zi],i=1,…,N,设置迭代计数器g=0,变异概率Pm,选择遗传数量L,交叉概率Pc,最大进化代数G。
(2)个体评价。根据适应性函数计算群体中个体的适应度并排序。由于角度是最主要的约束条件,TDoA 作为次要的约束条件,因此提出基于权重的判定方式,分别给角度差之和与TDoA 差之和赋予不同的权重ω1和ω2,那么可以将这个优化问题写为:
式中:Δ1和Δ2分别表示角度差和TDoA 差值。Δ1可以表示为:
式中:Φ1与Φ2分别表示当前搜索位置相对于基站1 和基站2 位置所得的角度与参数估计角度之间的差值;θ1与分别表示终端估计得到基站1 的离开方位角和当前搜索位置与基站1 的相对位置所计算得到的离开方位角;ϕ1与分别表示终端估计得到基站1 的离开仰角和当前搜索位置与基站1 的相对位置所计算得到的离开仰角;||·||1表示为1-范数。式中Φ2的计算方式与Φ1相似。Δ2可以表示为:
式中:c为光速;||·||2表示为2-范数;d1与d2分别表示当前搜索位置到基站的距离。
(3)交叉运算。在种群中选择成对的个体,以一定的概率交换它们之间的部分染色体,产生新的个体,即当选择两个个体时,产生一个[0,1]之间的随机数,若随机数小于交叉概率值,则对个体进行部分染色体交换,其中某个基因发生交换也是随机进行。反之,若随机数大于交叉概率值,则不发生交换。
(4)变异运算。通过种群数量与变异概率计算变异个体的数量并随机选择变异的个体;选定变异个体之后,随机对其中的部分基因选择变异,在本文中,基因的变异是在对应解空间中产生一个随机数作为变异值。
(5)选择运算。保留当前群体中最优的前L个个体到下一代群体中,随机在下一代群体中选择L个个体并进行替换。
(6)中值条件判断。本文中的中值条件为两种。第1 种设置了收敛值,当个体最佳适应度值小于收敛值时,则停止迭代并输出最佳适应度值的个体作为最优解。第2 种为g>G时,停止迭代,输出整个进化过程中最佳适应度值作为最优解输出,反之则g=g+1。
2 性能评估
2.1 实验设置
本文使用MATLAB 2022b 构建了一个典型的室内场景模型,模型大小为8×14×3 m3,如图4 所示。仿真设置两个5G 小基站,坐标分别为BS1=[0,14,3]T,BS2=[8,14,3]T。仿真设置频率为10 GHz,带宽为200 MHz,仿真信噪比为5 dB。
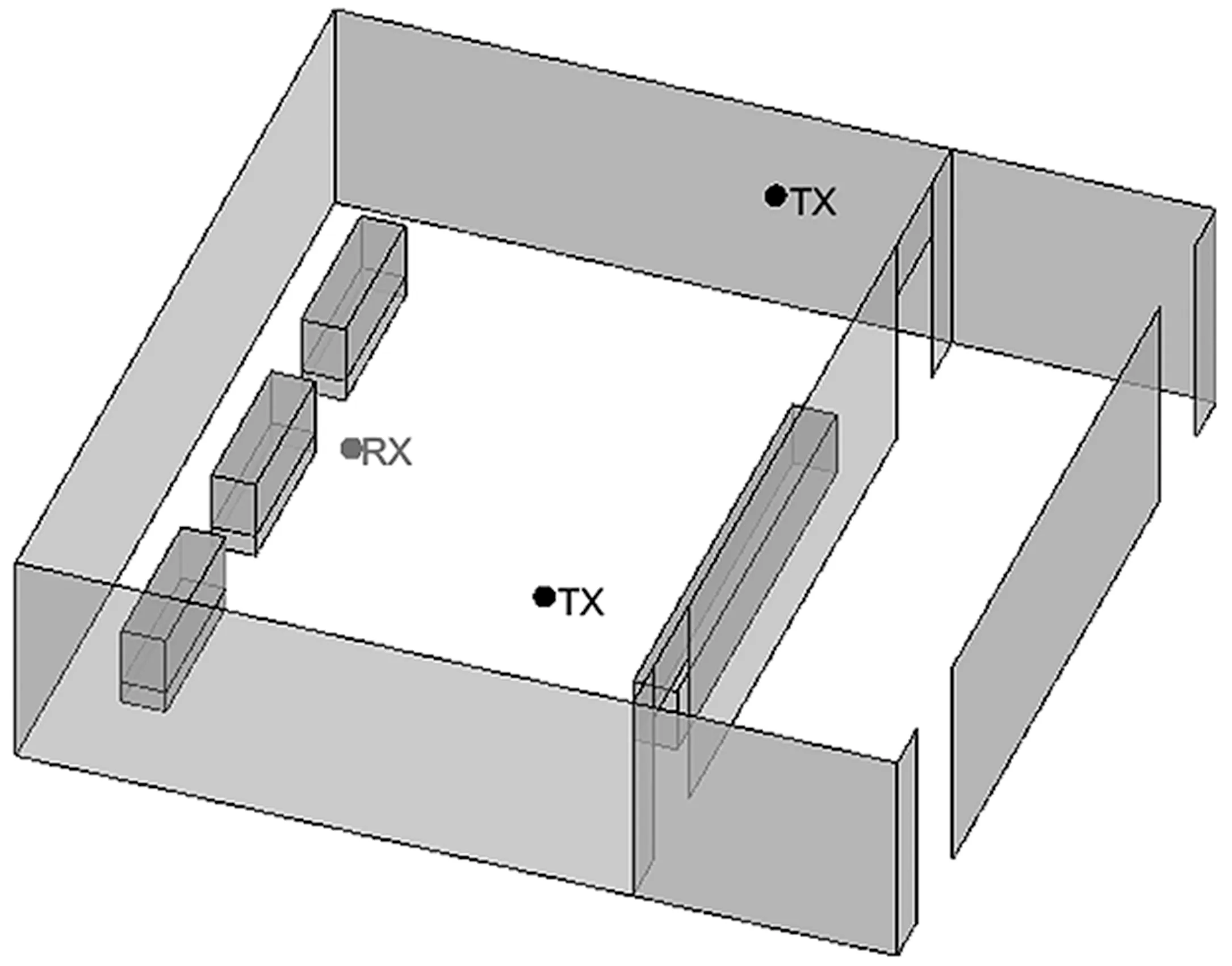
图4 室内场景仿真
2.2 角度误差
本文在目标定位实现之前进行了角度仿真评估实验,并得到了如图5 所示的结果,其中CDFs 为累积分布函数值。实验中,使用了4个天线发送信号,并使用终端的单个天线进行接收。实验结果显示,离开方位角的中值误差为6.18°,离开仰角的中值误差为6.25°。这表明所提出的角度测量方法在仅使用有限天线进行信号传输的情况下,仍能准确测量角度,为后续目标定位的可行性提供了有力支持。

图5 角度误差
2.3 总体定位误差
本文使用MATLAB 对室内真实环境进行建模,并进行了室内定位的仿真实验。结果如图6 所示。在2D 平面上进行定位时,中值定位误差为0.92 m。而在3D空间中进行定位时,中值定位误差为1.12 m。仿真结果充分证明了本文提出算法的可行性和有效性,能够满足实际应用的需求。
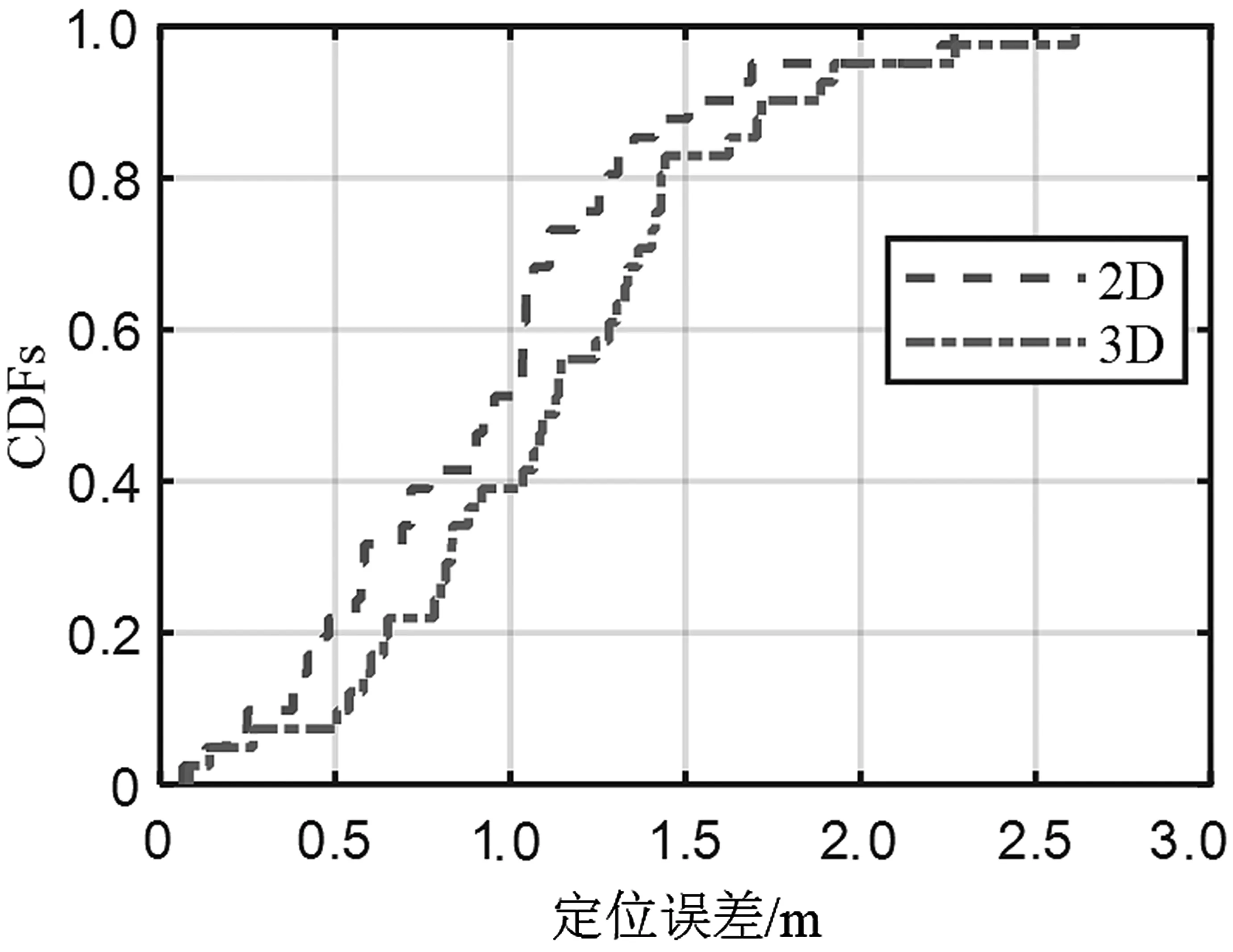
图6 总体定位误差
2.4 影响因素分析
2.4.1 信噪比对定位精度的影响
为了验证本文所提出的算法在不同信噪比情况下的定位精度,进行了一系列实验并得到了图7 中的定位结果。实验中设置了信噪比从-5 dB 到15 dB 的不同情况。结果显示,随着信噪比的增加,定位误差逐渐减小。在信噪比为-5 dB 时,中值定位误差为1.53 m;在信噪比为5 dB 时,中值定位误差为1.12 m;在信噪比为15 dB 时,中值定位误差为0.78 m。这是因为随着信噪比的增大,随机噪声减小,角度测量的误差变小,因此,定位误差降低。实验表明即使在低信噪比的情况下,本文提出的算法仍能在3D 空间中实现较好的定位精度。
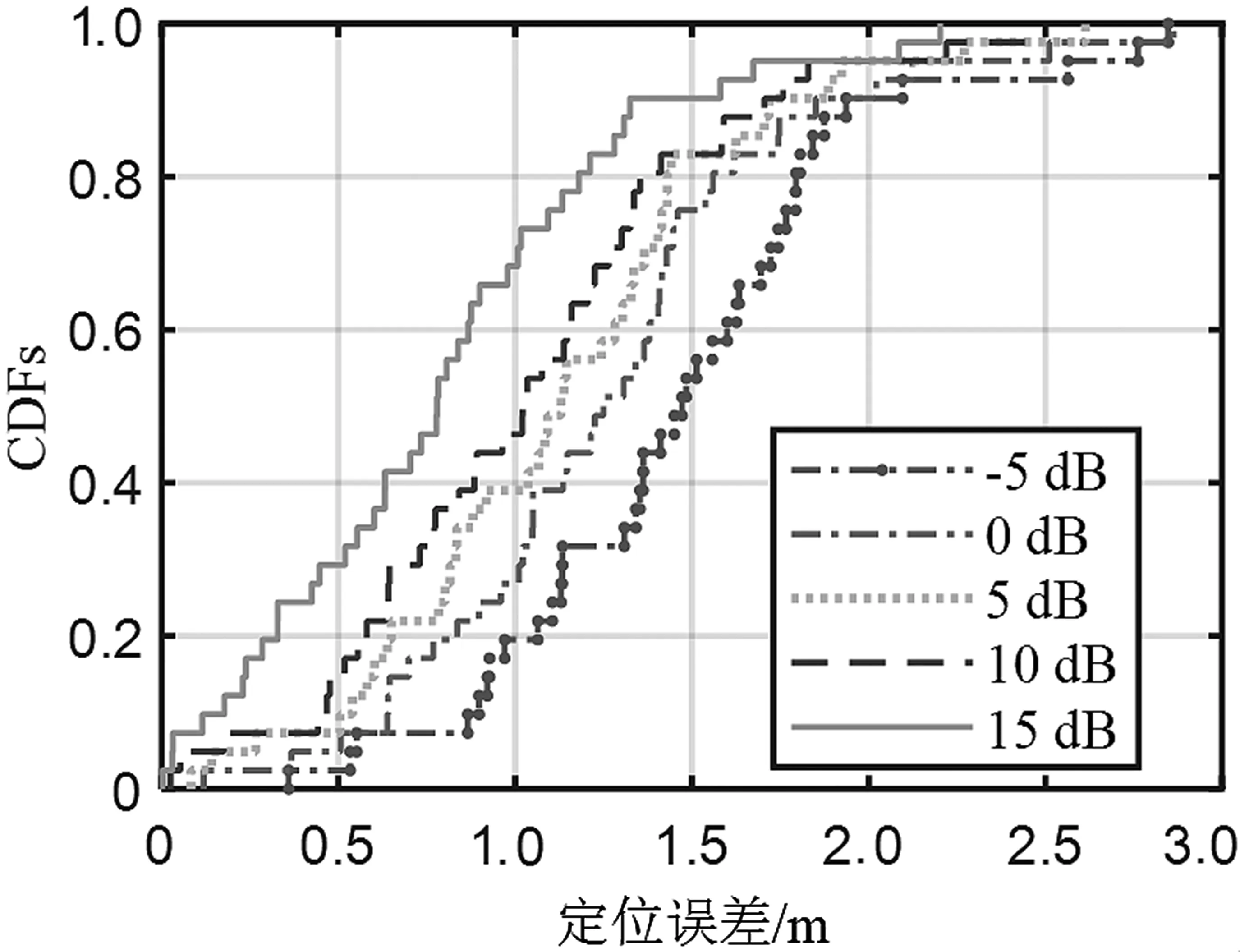
图7 不同信噪比定位精度对比
2.4.2 天线数量对定位精度的影响
考虑到天线数量对角度测量精度和定位精度的影响,实验中采用了4 个、6 个和8 个天线进行性能验证。结果如图8 显示,在使用4 个天线进行定位时,3D 空间中的中值定位误差为1.12 m。当天线数量为6 个时,中值定位误差为0.91 m。增加到8 个天线时,误差进一步降低至0.69 m。由此可见,增加天线数量可以提高角度测量的精度,并进而提高定位的精度。但即使只使用4 个天线,本文提出的算法仍能在3D 空间中实现可接受的定位精度。
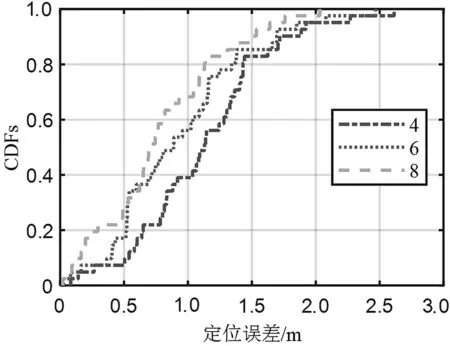
图8 不同天线数量定位精度对比
3 结语
本文提出了一种基于5G 小基站的终端3D 定位算法,该算法具有以下优点:(1)通过在终端进行定位,可以有效避免用户信息泄露,并减轻基站端的负载;(2)通过估计离开方位角和离开仰角,构建了适用于3D 空间的几何定位模型,并利用TDoA 对解空间进行约束。然而,由于方程是欠定的,因此本文提出了基于GA 的目标位置搜索算法,以完成目标的定位。仿真实验的结果表明,本文提出的算法在室内3D 空间中可以有效解决目标的定位问题。未来的工作将包括实际场景测试,以验证算法在实际环境中的性能表现,并进一步分析终端天线姿态对定位结果的影响以满足不同应用场景的需求。

