不同隧洞围岩压力计算方法对管片力学特性影响研究

刘启波，方腾卫，张建伟，刘 贺，江 琦

(1.广东省水利电力勘测设计研究院有限公司，广东 广州 510170；2.华北水利水电大学水利学院，河南 郑州 450046)

全断面隧道岩石掘进机(Tunnel Boring Machine，简称TBM)对围岩的扰动较小；TBM开挖施工减少了施工作业人员，机械化程度较高，极大地改善了施工的安全性和工作环境，工期也大幅度减少；TBM隧洞过流断面水力学特性好，因此在隧洞工程中被广为采用。管片结构是TBM这一施工工法的主要承载部件，管片结构的力学特性研究变得尤为重要，更是影响着整个工程的质量与安全[1-2]。

针对TBM隧洞管片力学特性及围岩压力计算方法的研究，前人进行了大量工作。赵大洲等[3]基于南水北调西线一期工程中深埋长隧洞的设计施工问题进行研究分析，通过建立三维有限元模型分析研究Ⅲ类围岩下围岩变形及内外水压力作用对管片结构安全稳定性的影响。佘成学等[4]以青松水电站有压引水隧洞工程为基础，通过建立有压引水隧洞三维有限元模型计算分析灌浆层及高内水压力作用对管片接缝变形等的影响。刘谦彬等[5]以位于喜马拉雅山脉的巴瑞巴贝引水隧道工程为基础，通过在管片衬砌外侧安装土压力盒、水压力计分析研究管片所受外部水土压力分布规律，并通过在管片安装前预埋的应变计来间接地监测管片结构的受力情况及力学特性。陈俊生等[6]以广州地铁盾构隧道工程为研究对象，通过建立盾构施工有限元模型，对施工阶段管片结构进行力学特性分析，得出千斤顶对管片结构在施工期造成的不利影响最大。李鹏飞等[7]通过对常见的全土柱理论、普氏公式、太沙基公式等7种隧道围岩压力计算方法进行比较分析，归纳总结不同围岩压力计算方法的优缺点及适用范围。韩兴博等[8]通过对多处盾构法隧道及新奥法隧道进行围岩压力现场测试，分析研究盾构隧道围岩压力分布规律和作用模式及不同围岩压力计算公式对盾构隧道的适用性。虽然上述学者对管片衬砌在围岩压力及内外水压力等组合工况作用下的力学特性和不同围岩压力计算方法适用性进行了大量的研究，但是都没有考虑到围岩压力计算方法对管片结构力学特性的影响。

隧洞地下结构设计计算一般有经验设计法、实用设计法、作用与反作用模型(荷载-结构法)、连续介质法、地层-结构法等[10-13]。目前采用的计算方法大多以荷载-结构模型为基础，将围岩视作施载体而非承载体[14-15]。然而TBM隧洞开挖的施工工法其特点就是进行衬砌结构的快速连续支护与安装，在进行隧洞开挖完成以后，隧洞围岩压力尚未释放时立即进行管片衬砌结构的安装，形成“管片-围岩”组合结构，共同成为统一的受力体系，因此选用地层-结构法，更有利于TBM管片的力学特性研究[16]。

综上，本文以榕江关埠引水工程中Ⅴ类围岩TBM输水隧洞区间段为研究对象，基于全土柱理论、SL 279—2016《水工隧洞设计规范》与普氏理论3种围岩压力计算方法并结合三维有限元软件，采用地层-结构法建立计算模型分析管片的应力状态及位移变化规律，研究管片结构的稳定性，并比较分析全土柱理论、SL 279—2016与普氏理论3种围岩压力计算方法的适用性。

1 工程概况及地质条件

1.1 工程概况

榕江关埠引水工程输水线路总长35.266km，由取水口及箱涵段、引水盾构隧洞、加压泵站、加压泵站至输水隧洞埋管段、输水隧洞(TBM隧洞)、输水明渠、分水池及出水闸等建筑物组成。其中输水隧洞长约27.055km，此段输水线路主要采用隧洞方案。该地区地层大部分为Ⅱ类和Ⅲ类围岩为主，围岩条件较好，岩质坚硬，但是其中分布少量Ⅳ类及Ⅴ类围岩，围岩强度低，岩体较破碎，因此该部分隧洞工程的建设主要采用对围岩条件适应性强的TBM法进行施工开挖，并以传统的钻爆法辅助施工。Ⅴ类围岩TBM输水隧洞区间段处于全风化花岗岩层，该区间隧洞埋深为51m，衬砌型式采用管片衬砌，管片衬砌内径为4.3m，外径为4.8m，开挖洞径为5.06m，管片外侧与围岩之间充填豆砾石并灌注水泥浆。

1.2 地质条件

工程区内主要为燕山二期中粗粒黑云母花岗岩，地质构造较简单，褶皱不发育，主要构造形迹以陡倾角发育的断裂为主。工程区内规模较大的断层共发育14条，宽1～5m不等，两侧断层影响带宽约10～50m不等。断层走向主要为北西向，与冲沟走向基本一致，倾向北东或南西的陡倾角断层为主，与隧洞夹角多为30°～70°。断层带主要发育糜棱岩断层泥、压碎岩、角砾岩、石英脉等，断层带内偶夹弱风化岩裂隙密集破碎带。部分断层规模较大，断层影响带宽30～50m，对围岩稳定性影响较大，容易产生较大掉块、洞壁失稳、洞顶坍塌等破坏现象。

2 围岩压力计算方法及计算过程

Ⅴ类围岩无二次衬砌TBM有压输水隧洞的安全稳定性研究依据全土柱理论、SL 279—2016和普氏理论这3种方法进行围岩压力的计算。

2.1 全土柱理论计算法

全土柱理论计算方法[17]仅考虑了隧洞埋深的影响，未考虑隧洞跨度的影响，因此在进行有限元计算分析时，依据隧洞的实际埋深建立有限元模型的上覆土体的厚度。

2.2 SL 279—2016计算法

围岩压力：

根据工程现场情况判断，围岩压力的荷载计算更趋向于SL 279—2016[18]的9.2.4中第5条：薄层状及碎裂散体结构的围岩，作用在衬砌上的围岩压力可按下式计算：

垂直方向qv=(0.2～0.3)γRb

(1)

水平方向qh=(0.05～0.10)γRh

(2)

式中，qv—垂直均布围岩压力，kN/m2；qh—水平均布围岩压力，kN/m2；γR—岩体容重，kN/m3；b—隧洞开挖宽度，m；h—隧洞开挖高度，m。

由工程的基本资料可知，隧洞开挖洞径为5.06m。通过上述描述计算可得：由SL 279—2016计算出来的有效土柱深度为1.032m，垂直方向的围岩压力qv=25.79kPa，水平方向的围岩压力qh=12.89kPa。

2.3 普氏理论计算法

围岩压力：

按照普氏理论[19]计算围岩压力，计算过程如下：

(1)判断TBM有压输水隧洞是否为深埋段

按照普氏理论，隧洞深埋与浅埋的分界深度H分界为：

(3)

式中，B—隧洞开挖断面宽度，m；h—隧洞开挖断面高度，m；f—围岩坚固系数。

通过上述公式计算，将系数取到最大值为2.5时，计算得出H分界=6.34m，由此得出TBM有压输水隧洞为深埋。

(2)确定有效土柱深度

根据普氏理论的基本内容可按照下式计算有效的土柱深度：

(4)

(5)

式中，a1—自然平衡拱的最大跨度，m；b1—自然平衡拱的最大高度，m。

由基本资料的数据可以计算得出有效土柱深度范围是1.9～3.81m。

(3)确定围岩压力数值

普氏认为，作用在深埋松散岩体洞室顶部的围岩压力仅为拱内岩体的自重。但是，在工程中通常为了方便，将洞顶的最大围岩压力作为均布荷载，不计洞轴线的变化而引起的围岩压力变化。据此，洞顶最大围岩压力可按下式计算：

(6)

普氏围岩压力理论中的侧向压力可按下式计算：

(7)

(8)

计算得出竖向围岩压力范围q为47.573～95.146kPa；侧向压力e1=7.913kPa，e2=55.392kPa。

2.4 理论比较

依据全土柱理论的围岩压力计算方法，围岩压力的大小只与隧洞的埋深有关，且隧洞实际埋深为51m，所以全土柱理论计算的围岩压力最大；依据SL 279—2016计算出来的有效土柱深度为1.032m，垂直方向的围岩压力qv=25.79kPa，水平方向的围岩压力qh=12.89kPa；依据普氏理论计算出来的有效土柱深度为1.9～3.81m，垂直方向的围岩压力范围q为47.573～95.146kPa；水平方向的围岩压力e1=7.913kPa，e2=55.392kPa。

3 TBM有压输水隧洞精细化模拟

3.1 精细化模型及边界条件

以榕江关埠引水工程中Ⅴ类围岩TBM输水隧洞区间段为研究对象，建立TBM有压输水隧洞安全精细化模型。根据全土柱理论、SL 279—2016和普氏理论计算出的有效土柱深度的不同，隧洞的埋深也不相同，三维有限元整体模型如图1所示。模型主要包括围岩层、固结灌浆层、豆砾石灌浆层和管片层。模型尺寸以隧洞中心点为起点分别向左、向右、向下延伸3倍洞径，隧洞开挖方向长度为23m，其包括两端的边界效应区域。模型网格剖分主要以规则六面体单元为主，减少计算中力传递产生的应力集中现象。模型中用面-面接触模拟管片层与豆砾石灌浆层、豆砾石灌浆层与围岩之间的相互作用，即法向上定义为硬接触，允许接触面之间发生分离；切向上服从库伦摩擦定律，当切向应力达到临界值后允许发生滑移，摩擦系数取0.5[20]。

图1 TBM有压输水隧洞安全精细化三维模型

模型左右边界施加x方向的法向约束，前后边界施加z方向的法向约束，底部边界施加全约束。

数值模拟计算中，围岩、管片、豆砾石灌浆层均采用三维实体单元(C3D8R)模拟，隧洞围岩采用Mohr-Coulomb屈服准则本构模型，钢筋混凝土管片及豆砾石灌浆层则采用线弹性本构模型。材料参数见表1。

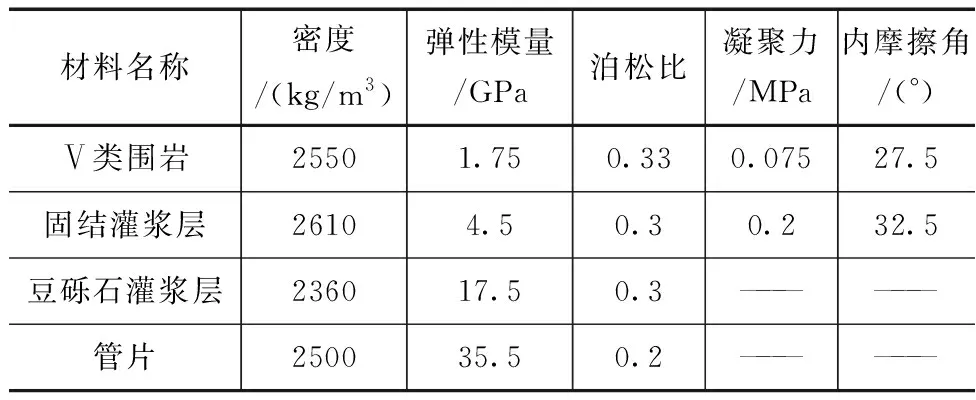
表1 有限元材料计算的参数

3.2 加载方式

在进行数值计算分析时，首先进行地应力平衡模拟初始地应力场，保证围岩结构初始地应力状态的正确性。管片结构外表面沿高度方向施加不均匀分布的外水压力；内表面沿高度方向施加不均匀分布的内水压力。

3.3 计算工况及荷载

为探究不同荷载组合工况对隧洞结构的力学特性的影响，揭示其应力、位移等变化规律，以期为其结构设计及运行管理提供理论参考。结合工程实际，设置4种荷载组合工况，开展隧洞结构有限元计算，具体如下：

工况1：隧洞穿越典型区段围岩压力作用工况；

工况2：隧洞穿越典型区段围岩压力+外水压力作用工况；

工况3：隧洞穿越典型区段围岩压力+内水压力作用工况；

工况4：隧洞穿越典型区段围岩压力+内水压力+外水压力作用工况。

各计算工况的荷载组合方式见表2。

表2 各个工况荷载组合

4 管片力学特性分析

为了研究无二次衬砌TBM有压输水隧洞的安全稳定性，对不同荷载组合工况作用下同一参考断面的应力及位移进行对比分析[21-22]。

4.1 管片拉应力分析

工况1围岩压力荷载作用下，不同围岩压力计算方法的管片最大主应力云图如图2所示。由图可知，在全土柱理论计算方法下管片的较大拉应力区主要发生在拱顶、拱底及管片拱顶和拱底边缘区域，所受拉应力的最大值为1.866MPa；在SL 279—2016计算方法下，管片无受拉区；在普氏理论有效土柱深度为1.9m时，管片的较大拉应力区主要发生在拱顶内侧区域，所受拉应力的最大值为4.222kPa；在普氏理论有效土柱深度为3.81m时，管片的较大拉应力区主要发生在拱顶内侧区域，所受拉应力的最大值为9.888kPa。管片的最大拉应力均小于SL 191—2008《水工混凝土结构设计规范》C55混凝土抗拉强度标准值2.740MPa，均满足规范要求。

图2 管片最大主应力云图

不同荷载组合工况作用下，同一参考断面的最大主应力最大值结果对比图，如图3所示。在基于全土柱理论方法进行计算分析时，不同荷载组合工况在管片结构上产生的最大主应力的最大值均为正值(即管片结构存在受拉区)；在基于SL 279—2016计算的围岩压力作用下，不同荷载组合工况在管片结构上产生的最大主应力的最大值均为负值(即管片结构无受拉区)；在普氏理论有效土柱深度为1.9m的围岩压力作用下，在仅有围岩压力和在检修期有围岩压力和外水压力作用下，在管片结构上产生的最大主应力的最大值为正值；在普氏理论有效土柱深度为3.81m的围岩压力作用下，不同荷载组合工况在管片结构上产生的最大主应力的最大值均为正值。

图3 管片最大主应力最大值结果对比图

围岩压力的大小会对管片结构是否产生受拉区产生一定的影响，因此在进行管片结构安全稳定性研究时，应根据施工现场的实际情况选取合理的围岩压力计算方法，保证研究结果的正确性与合理性。

4.2 管片压应力分析

工况1围岩压力荷载作用下，不同围岩压力计算方法的管片最小主应力云图如图4所示。由图可知，在全土柱理论计算方法下管片承受最大压应力区域位于拱腰内侧区域，所受压应力的最大值为15.660MPa；在SL 279—2016计算方法下，管片承受的最大压应力区域位于拱顶外侧区域，所受压应力的最大值为189.800kPa；在普氏理论有效土柱深度为1.9m时，管片承受最大压应力区域位于拱顶外侧区域及拱顶与拱腰之间的内侧区域，所受压应力的最大值为476.300kPa；在普氏理论有效土柱深度为3.81m时，管片承受最大压应力区域位于拱顶外侧区域及拱顶与拱腰之间的内侧区域，所受压应力的最大值为881kPa。管片的最大压应力均小于SL191—2008 C55混凝土抗压强度标准值35.500MPa，均符合规范标准。

图4 管片最小主应力云图

不同荷载组合工况作用下，同一参考断面的压应力最大值结果对比图，如图5所示。基于全土柱理论计算的围岩压力作用下不同荷载组合工况在管片结构上产生的最大压应力均远大于普氏理论与SL 279—2016；基于普氏理论有效土柱深度为3.81m时的围岩压力作用下不同荷载组合工况在管片结构上产生的压应力的最大值均大于普氏理论有效土柱深度为1.9m时；采用SL 279—2016计算的围岩压力作用下不同荷载组合工况在管片结构上产生的最大压应力均为最小。

图5 管片压应力结果对比图

随着围岩压力的增大，管片结构承受的最大压应力也越来越大。并且无论在基于哪种理论计算的围岩压力条件下，均在检修期围岩压力和外水压力共同作用下产生的压应力最大。围岩压力的大小以及外水压力的作用会对管片结构所承受的压应力产生一定的影响。因此在进行管片结构安全稳定性研究时，应根据施工现场的实际情况选取合理的围岩压力计算方法及重点监测施工现场外水压力的大小。

4.3 管片竖向位移分析

工况1围岩压力荷载作用下，不同围岩压力计算方法的管片竖向位移云图如图6所示。由图可知，在全土柱理论计算方法下管片位移分布规律整体呈对称分布，且管片位移沿拱顶-拱腰-拱底基本呈逐渐减小的趋势，竖向变形位移最大值发生在拱顶位置，管片竖向相对位移为3.688mm；在SL 279—2016计算方法下，管片位移沿拱顶-拱腰-拱底呈逐渐减小的趋势，竖向变形位移最大值发生在拱顶位置，管片竖向相对位移为0.327mm；在普氏理论有效土柱深度为1.9m时，管片位移沿拱顶-拱腰-拱底呈逐渐减小的趋势，竖向变形位移最大值发生在拱顶位置，管片竖向相对位移为0.882mm；在普氏理论有效土柱深度为3.81m时，管片位移沿拱顶-拱腰-拱底呈逐渐减小的趋势，竖向变形位移最大值发生在拱顶位置，管片竖向相对位移为1.586mm。管片的最大竖向位移均满足GB 50446—2017《盾构法隧道施工及验收规范》中关于隧道衬砌结构竖向位移控制值判断准则小于10.000mm的要求。

图6 管片竖向位移云图

不同荷载组合工况下，同一参考断面的竖向相对位移结果对比图，如图7所示。基于全土柱理论计算的围岩压力作用下不同荷载组合工况在管片结构上产生的竖向相对位移均远大于SL 279—2016和普氏理论；基于普氏理论有效土柱深度为3.81m时的围岩压力作用下不同荷载组合工况在管片结构上产生的竖向相对位移均大于普氏理论有效土柱深度为1.9m时；采用SL 279—2016计算的围岩压力作用下不同荷载组合工况在管片结构上产生的竖向相对位移均为最小。

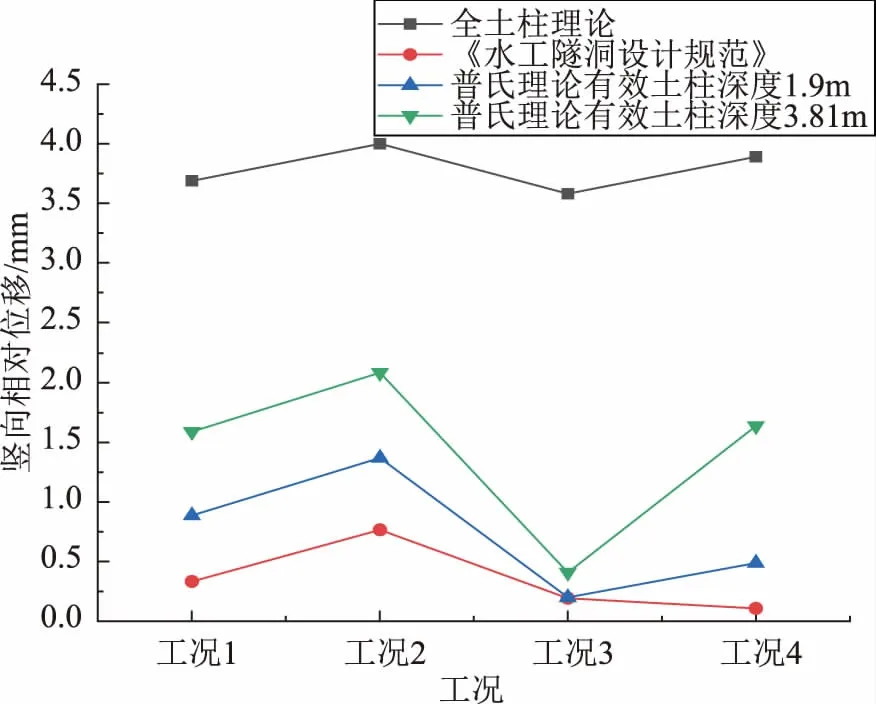
图7 管片竖向相对位移结果对比图

随着围岩压力的不断增大，管片结构产生的竖向相对位移也越来越大。并且无论在基于哪种理论计算的围岩压力条件下，均在检修期围岩压力和外水压力共同作用下产生的竖向相对位移最大。围岩压力的大小以及外水压力的作用会对管片结构所产生的竖向相对位移产生一定的影响。因此在进行管片结构安全稳定性研究时，应根据施工现场的实际情况选取合理的围岩压力计算方法及重点监测施工现场外水压力的大小。

5 结论

依据3种围岩压力计算方法基于地层-结构法建立有限元模型进行Ⅴ类围岩单层衬砌结构安全稳定性研究，主要结论如下：

(1)该工程依据3种围岩压力计算方法所得结果均满足规范要求，Ⅴ类围岩单层衬砌TBM有压输水隧洞处于安全状态。管片结构是否产生受拉区与围岩压力的大小有关，围岩压力较小的情况下，管片结构无受拉区。压应力和竖向相对位移最大值均出现在检修期围岩压力和外水压力共同作用下。

(2)在进行有压输水隧洞设计与研究时，在浅埋隧洞中可以选取全土柱理论进行围岩压力的计算；在深埋隧洞中，可以选取普氏理论进行围岩压力的计算，并依此进行有压输水隧洞的设计与研究。