混凝土喷雾系统喷雾优化的数值模拟

张 华，张高超

(华北电力大学水利与水电工程学院，北京 102206)

0 引言

在混凝土施工过程中，为防止温度应力导致混凝土裂缝，常采用混凝土温度控制措施[1-3]。关于温控措施Bhattarai等[4]从降低水化热的角度进行研究，提出了一种温度与水速的控制模型。李松辉等[5]通过总结几十个混凝土大坝的温控防裂技术，搭建了一套智能化监控体系。赵泽湖等[6]对混凝土拱坝进行通水冷却降温，通过对同仓温差对应力的影响进行研究，为后续对混凝土拱坝的温度控制以及防裂的研究提供了参考。侯骥等[7]根据不同的工程情况，采用有限元的方法对大坝铺设水管降温进行了数值模拟研究，并结合UDF对模型进行优化，为实际工程中的冷却参数提供了参考。同样，张健等[8]为了对隧洞衬砌混凝土温控进行研究，对工程中的泄洪洞衬砌进行了三维数值模拟，结果显示在10月份后对混凝土表面进行保温处理效果较好，为相关工程提供了参考。除此之外应用混凝土喷雾系统进行仓面喷雾也是一种仓面控温的重要手段，但由于喷雾系统管路的水头损失[9-11]，会导致沿管道所布置的喷嘴入口压强有较大的差异，从而影响整体喷雾的效果，为了更好地保证温控效果，大量学者对喷雾系统的稳定性展开了研究。

国内外的学者关于喷雾系统稳定性的研究，可追溯到单个喷嘴入口压强和流场特性。张永良等[12]建立了二维数值模型，对单个喷嘴雾化锥角流场结构等进行数值模拟，结果表明随着压强增加喷嘴表面波的扰动变大，雾化效果好；Miller等[13]通过实验研究，改变了喷嘴的结构，从三维的角度对射流冲击时压降和局部换热分布的影响，结果表明倒角处理后的喷嘴优化效果明显。出于对喷嘴入口压强的考虑，王新坤等[14]采用数值模拟和实验对比的研究方法，在不同的压强下对负压反馈射流喷头的水力性能进行研究，通过实验结果确定出了一种理想的结构参数，给后续对喷头的研究提供了新的方法。

许多学者对于喷嘴入口压强分布均匀性做了大量研究[15-16]。张学军等[17]参照旋转式喷头对新型微喷带进行了实验研究，分析其水量分布特性，并根据分布特性将微喷带分成了3类，可用于不同灌溉场所；除此之外，为了减少管路系统的压强分布不均匀性，田金霞等[18]通过在管路添加压力调节器，对喷头的入口压强进行调节，在不同流量下进行对比试验，结果表明通过增设调节器能够提高喷灌质量；张琛等[19]通过对模型边界条件进行改进，对不同结构和弹簧参数的压力调节器进行研究，得到了参数对初始调节压强的影响规律，研究结果表明，在改进边界条件后提高了调节效率，改善了调节性能。

目前喷雾系统中喷嘴沿管路均匀布置，通过增设压力调节器对喷嘴进口压强进行调节，使各个喷嘴的入口压强稳定在期望值附近，但是该方法使得系统的组件增多，增加了管路系统的复杂性。因此针对喷雾系统提出喷嘴变间距布置方式，来保证不同位置喷嘴进口压强的均匀性。采用键合图方法[20-21]对管路进行数学建模并求解，通过FLUENT喷雾数值模拟进行验证，结果表明喷嘴变间距排列是一种较好的布置方式，为喷雾系统稳定的研究提供了新的思路。

1 喷雾系统管路模型

1.1 混凝土喷雾降温系统

混凝土降温的水气二相流喷雾系统是由高压水泵、空气压缩机、高压输水管道、高压输气管道、雾化喷嘴等组成[2]，在仓面两侧沿程布置喷嘴对其进行喷雾降温，如图1所示。可以看出喷雾管路对称布置在仓面两侧，为了简化计算本文选取单侧高压供水管路为研究对象。

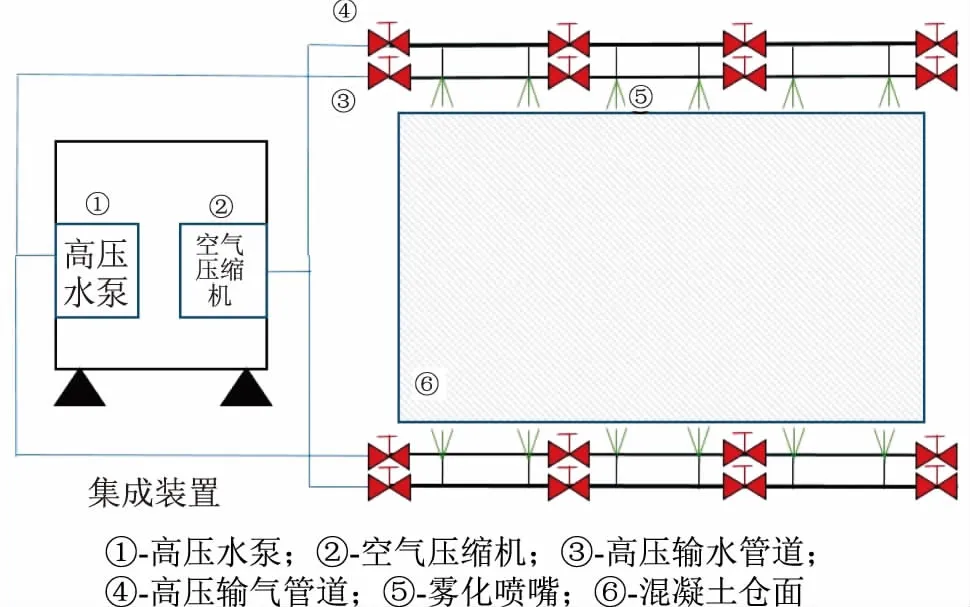
图1 混凝土喷雾降温系统

1.2 喷嘴布置优化方案

喷嘴布置示意图如图2(a)所示，均匀布置在管路上。在混凝土仓面以顶点O为原点，以仓面宽为x轴，长为y轴，垂直于仓面方向为z轴，建立坐标系Oxyz。设喷嘴布置高度z=7m，喷嘴水平位置，y∈(0，18)。

图2 喷嘴布置方式

在管路上均匀布置6个喷嘴进行喷雾，每个喷嘴间距为3m，设流量Q=6.72×10-4m3/s，初始压强p0=0.5MPa。文献[22]通过实验研究喷嘴的喷雾特性，用高速摄影机记录雾化锥角随喷嘴入口压强的变化，结果表明随着压强的增大雾化锥角增大，喷雾效果提升。因此针对喷嘴入口压强对雾化效果的影响[21]，提出了等比布置、等差布置，两种变间距布置方案对传统布置方式进行改进。对这两种布置，分别设立了3组不同工况进行对比，等差工况见表1，等比工况见表2。

表1 等差(d)布置工况

表2 等比(q)布置工况

1.3 系统管路键合图建模

1.3.1模型验证

键合图是从功率流的角度对系统特性进行分析的一种工具，可以把一个系统看成由多个子系统组成，进而反映出研究系统中的功率流向和各个功率之间的作用关系。键合图的组成元素包括：C、I、R、Se、Sf、GY、TF、“0”结点、“1”结点。C表示液容，I表示液感，R表示液阻，Se表示力源，Sf表示流源，GY表示旋转器，TF表示转换器。

考虑单喷嘴工况下的管路压强情况。管路进口初始压强设为3MPa。根据键合图的规则建立了喷雾系统中的高压供水管路的一维数学模型，如图3所示。图3中，ei(i=1，2…n)；fj(j=1，2…n)分别表示功率键上的势变量、流变量。

图3 单喷嘴管路键合图

管路的键合图中箭头表示功率的流向，各个状态变量通过1结点和0结点连接，根据图3可以得到管路系统对应的状态方程如下：

(1)

(2)

式中，p3、q6—压强、流量；Se—系统的压强源项；I—管路中的液感；R、R1—液阻，C—管路的液容。

利用Simulink对状态方程(1)、(2)进行求解，仿真结果如图4所示。由图4可知，喷嘴进口处的压强从0MPa开始快速增长，t=0.1s时，压强为2.06MPa，压强增长率逐渐变小；当t=0.45s时，压强达到2.8MPa，随后保持不变，可视为进入恒定流阶段。而对于输水管路的恒定流，根据伯努利方程和柯列布鲁克-怀特(Cole-brook &White)经验关系式，计算得到压强为2.84MPa。本文数值模拟结果能够刻画输水管路的压强动态特性，其压强的稳定值与恒定流的计算值相对误差为1.6%，验证了键合图模型的准确性。

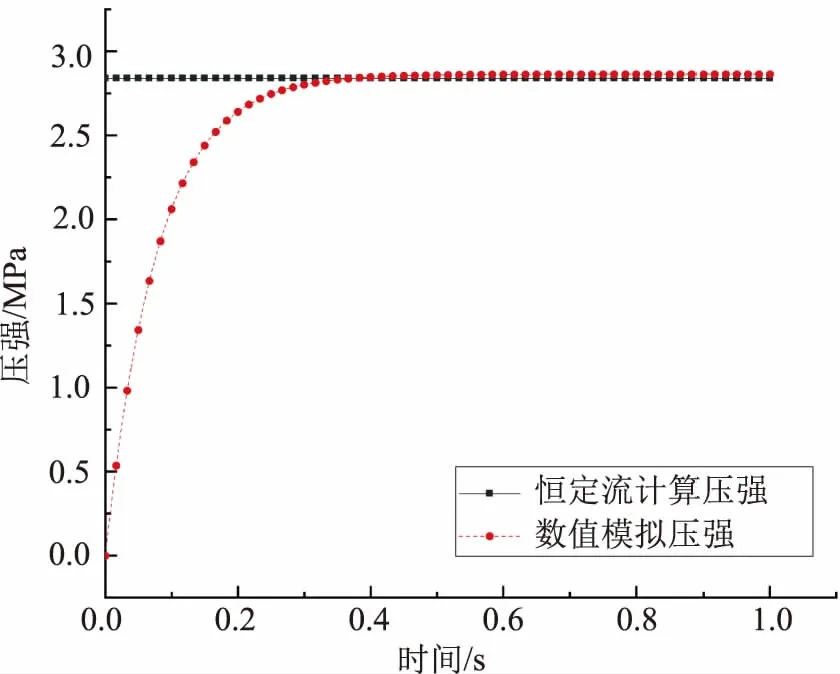
图4 单喷嘴模型验证结果

1.3.2键合图模型及状态方程

考虑到管路的液阻，液感、液容对系统的影响，将管路系统视为恒压情况进行分析，将喷嘴与管路的连接处、管路间与阀门连接处，视为阻性元件。为了对管路系统从非恒定流到恒定流的工作过程进行动态模拟，采用键合图方法对管路进行建模，采用分段集中参数的办法，根据喷嘴出口处位置将管道分成5段，如图5所示。其中，Se表示供水压强，MPa；I1—I6表示液感，kg/m4；R1—R6表示液阻，Ns/m5；C1—C6表示液容，m2/N；e1—e36、f1—f36分别表示功率键上的势变量、流变量。

图5 喷雾管路的键合图

得出系统的状态方程如下：

(3)

式中，n∈[1，4]，且n为整数。

2 仿真结果分析

2.1 喷嘴布置方式的影响

为了从表1—2提出的工况中选出最优的布置方式。首先，从均匀度的角度对不同布置方式的压强分布进行定量分析。采用均匀度对任意一组数据进行分析时，根据该组数据的平均数与这组数据中的每个数据的差，再分别与平均值作比较。均匀度的绝对值越小表示系统压强分布更加集中，均匀度用s表示，计算公式如下：

(4)

根据公式(4)可得出不同工况下的均匀度，如图6所示。显然当喷嘴的布置方式按照等差分布排列时，压强均匀度绝对值相对较小，以第一个喷嘴为例，如图6(a)所示，在等差布置下，喷嘴的均匀度明显低于均匀布置，表明该布置下压强分布更加均匀。从图6(b)可以看出在前2个喷嘴等比布置效果略差，而后面4个喷嘴的情况比均匀布置情况较好。因此可以看出，这两种布置方式在一定程度上可以提高管路压强的均匀度，并且等比布置的效果更好。

图6 不同布置方式下的均匀度

根据喷嘴的雾化锥角及水平喷雾的距离可以估算出喷嘴间距不小于2m，因此，结合以上讨论，在3组工况下的对比中选出最佳公差d=0.3，最佳公比q=0.88。

2.2 变间距布置的对比

根据系统状态方程(3)，利用Simulink的模块化程序语言进行求解，将最小时间步长设为0.01s，仿真时间设为1s，为了保证计算的高效准确，在进行仿真时求解器采用Variable-step的ode-45对管路均匀分布，等差分布，等比分布3种方式分别进行求解，压强曲线如图7所示。可以看出，对于同一个位置的喷嘴随着仿真时间的推进，压强曲线的增长曲率跟喷嘴的布置距离成反比。进口处的压强在仿真时间0.48s左右基本保持稳定。通过比较3种布置方式下同一个喷嘴的压强曲线可以看出，均匀布置时仿真分析相对误差是2%，等差布置时仿真相对误差是2.1%，等比布置时相对误差是3.15%，均在合理的范围内。

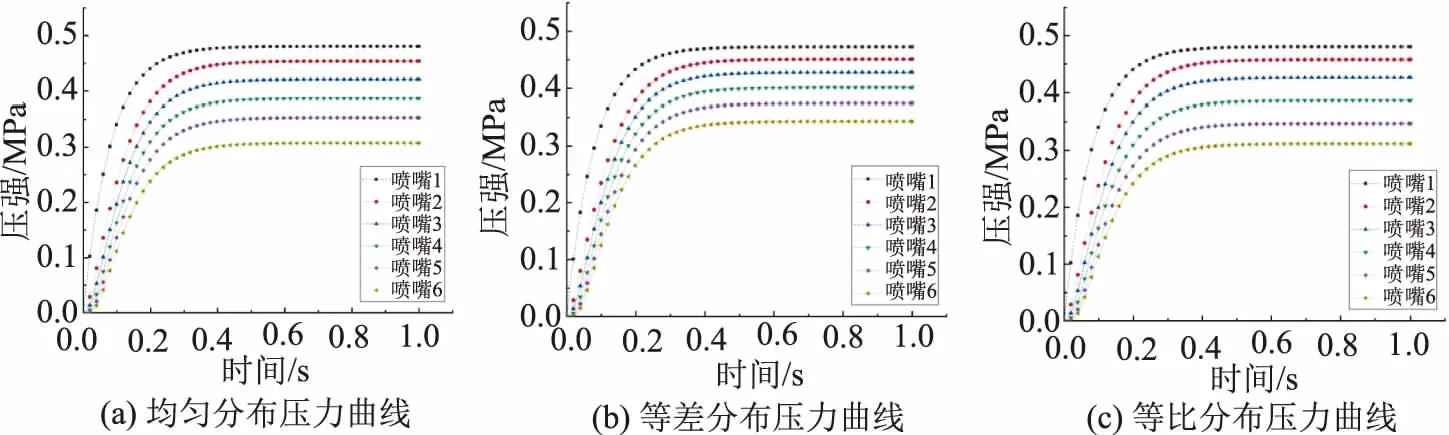
图7 不同布置方式下喷嘴的压强分布曲线

通过对3种布置方式下的不均匀系数，方差求解，结果见表3。将结果绘制如图8—9所示，从图8可以明显看出，在布置方式为等差布置时效果变化最明显，该布置方式的不均匀系数比均匀分布减小34.3%；从图9可以看出，等差布置下方差明显减小。因此，改变了喷嘴传统的布置方式，一定程度上提高了管路压强的均匀性，进而能保证喷雾系统高效工作。

表3 不同布置方式下的参数结果

图8 不同布置方式不均匀系数

图9 不同布置方式方差

3 优化方案的喷雾数值模拟

3.1 计算域的建立

为了减小混凝土喷雾数值模拟的复杂性，把混凝土仓面看作一块形状规则的长方体，如图10所示，其中混凝土块A1的长、宽、高分别为18、8、5m。在采用数值模拟对仓面喷雾效果进行计算流体力学分析的过程中，设置一定范围的计算域更能保证模拟结果的准确性，从而更好地反映出实际工程中的现象，因此在混凝土块外部空间建立一个计算域，如图10中A2所示，计算域内视为充满了空气。

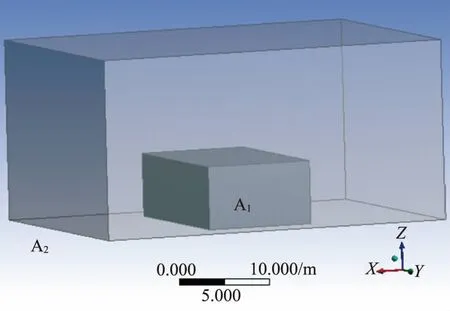
图10 喷雾模型及计算域

对喷雾系统进行数值模拟，需要设定合理的边界条件，主要的边界条件包括压力出口边界(Pressure outlet)和壁面(Wall)两种。把计算域范围内设成空气材料，喷嘴将颗粒喷射到仓面上，生成的雾滴在计算域内进行随机不规则运动，使得计算域内的空气产生扰动，将计算域的四周设为压力出口，操作压力设为标准大气压，其余面均设为壁面。

3.2 网格无关性检验

网格的质量直接影响了计算的速度和精度，为了能够验证模拟结果的可靠性，在CFD数值模拟之前，进行网格无关性检验是一项十分必要的工作。当选择网格的数量合适的时候，不仅可以加快数值模拟的运算速度，同时计算结果的准确性也会提高。在进行数值模拟的过程中，使用结构化网格计算可以降低网格的数量，能够使计算结果更快收敛。

本文以仓面上的雾滴的SMD为参考标准来进行网格无关性检验。分别选取了10万、20万、50万和100万的4种网格数量进行比较。根据数值模拟的结果显示，在不同网格数量下，仓面的SMD分别为89.7、86.3、83.2、82.66μm，结果如图11所示。可以看出，网格数量从20万到50万SMD变化值为3.11μm，50万到100万网格的变化值为1.66μm，变化很小。因此本文选用50万网格数量进行计算。

图11 网格无关性检验

3.3 模型验证

为了对喷雾场的设置进行可行性验证，根据文献[23]中的实验做模型对照，在对喷雾效果分析的过程中雾滴的SMD是一个常用的标准。因此建立一个简易的喷雾场，如图12所示，以地面矩形的正中心为原点o，沿着边长分别设为x轴、y轴，垂直地面向上方向为z轴。在计算喷雾场的顶面中心处设置垂直向下的喷嘴P1。

图12 模型验证喷雾场

根据文献[23]中的工况，选取压强4、5、6MPa进行模拟，通过统计喷雾场底面的SMD并与实验结果进行对比，结果见表4。可以看出，在喷雾场选用与文献[23]实验相同的工况进行计算时，发现数值模拟的结果与实验值存在一定的误差，在不同的压强下可以看出相对误差分别为2.6%、6.2%、4.3%，误差结果均小于8%，可以认为喷雾模型精度满足模拟要求。

表4 底面SMD仿真结果与实验对比

3.4 不同布置方式对雾滴特性的影响

对均匀分布、等差分布和等比分布3种布置方式进行喷雾数值模拟，以特征粒径SMD为参照标准，对喷雾效果进行判断。3种布置方式下的雾滴空间分布如图13所示。

图13 不同布置方式的雾滴空间分布

从空间分布上看，3种方式效果均不错，均匀布置方式下，雾滴可全覆盖仓面，但是雾滴在空间的分布主要在上部，在混凝土宽度方向上分布较少，而等比和等差布置方式下，既能满足雾滴对仓面全覆盖的情况下，雾滴空间上的分布更加宽广，在空间环境中发生更多的随机碰并与破碎，从整体来看优化方案对喷雾雾滴的空间分布在一定程度上有提升。通过统计不同布置方式下的SMD发现，均匀布置方式下的SMD为28μm，等比分布的SMD为26.7μm，而等差布置下的SMD为20.1μm，相比起均匀布置，等比布置和等差布置的情况下SMD的分别减少4.6%和28.2%，可以看出在优化方案下，等差布置对喷雾的优化效果较好。

3.5 布置方式对仓面液膜厚度的影响

液膜厚度也可以用来评判雾化效果，3种布置方式下的液膜如图14所示。从3种工况的仓面液膜厚度可以看出，均匀布置时仓面液膜主要集中在仓面的中轴线，液膜厚度最大为73μm；等比布置时，液膜沿仓面中轴线向两侧延伸，分布较均匀布置时有了一定的改善，此布置方式下的最大液膜厚度为72.2μm；等差布置时可以明显看出，液膜在仓面的分布更加均匀，大概覆盖仓面的一半以上，且最大液膜厚度为70μm。液膜厚度大，表示仓面喷雾过程中会形成大量积水，对混凝土的冷却产生不利的影响。所以，从液膜厚度来看，等差布置方式下的雾化效果最好。

图14 不同布置方式仓面液膜厚度

4 结论

(1)采用键合图法建立了管路的一维数学模型，推导出了管路的状态方程，利用Simulink对状态方程进行求解，得到了系统管路的动态压强曲线。

(2)提出了两种喷雾系统管路变间距布置方式，通过对状态方程求解出的不同工况喷嘴入口压强分析，确定了等差和等比两种变间距布置的最佳公差为0.3，最佳公比为0.88。根据确定的变间距布置方式，通过对均匀度、不均匀系数、方差等不同参数的对比，结果表明等差布置对管路压强均匀度的调节效果较好。

(3)建立了混凝土仓面喷雾的三维数学模型。结果表明：均匀布置和变间距布置方式相比，变间距布置的喷雾场的雾滴空间分布更合理，从雾滴空间混乱度上来说，等差布置方式效果更好；最后对混凝土仓面的液膜厚度进行分析，结果显示，等差布置时，仓面的液膜厚度最小，沿着仓面中轴线分布更加均匀。从而验证了喷雾优化模型的可行性。