水电机组流激振荡数值仿真

郑 阳，刘宛莹，陈启卷，肖志怀

（武汉大学 水力机械过渡过程教育部重点实验室，湖北省武汉市 430072）

0 引言

低频振荡现象长期以来被视为现代电力系统运行安全稳定性的重大隐患之一。近年来，随着我国西南地区水电资源开发的蓬勃发展，出现了一系列具有水电高占比特点的电力系统，这些电力系统均存在着发生低频振荡（f∈0.1 ～2.5Hz）或超低频振荡（f<0.1Hz）的风险[1]。

文献[3]研究了送端含有大型水电机群的交直流混联系统中水电机组对电网低频振荡的影响及其有效抑制策略。文献[4]探索了水电机组调速系统模型参数对藏中电网超低频振荡的影响规律，系统分析了调速系统参数对低频振荡的影响和各类水击模型的适用范围。文献[5]对电站有压管道长度、管道水体振动模式与电力系统低频振荡频率间相关关系进行了分析；文献[6]研究了尾水位、水力损失等参数对机组超低频振荡的影响。

本文针对四川省某大型水电站机组运行过程中出现的与电站尾水流道水力不平衡密切相关的持续性有功功率超低频振荡现象，采取电路等效法构建电站尾水流道的微分方程组数学模型，并分别开展时域数值仿真与特征值分布规律分析。

1 水电站尾水系统电路等效模型

国内某大型水电站尾水系统为一洞两机布置型式，有压管道与无压隧洞连接的出流结构。尾水系统结构示意图如图1 所示，系统中各项水工建筑的结构参数设置参见文献[6]。

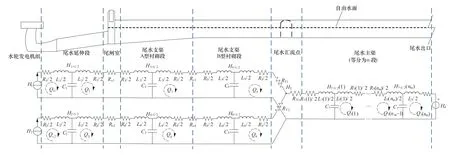
图1 某水电站明满流尾水系统电路等效模型Figure 1 Equivalent circuit model of the tailrace system of a hydropower plant with pipe and channel flows

通过引入有压管道与无压明渠的电路等效理论[6，7]，可以同时绘制出电站尾水系统的整体电路等效模型拓扑。模型中各水力组成元件的电路等效模型可参考文献[6]，根据基尔霍夫电压电流定律[8]，由于尾水流道主渠长度远大于其他各管、渠段，将其按长度等分为12 段，尾水系统其他管段均设为1 段。尾水系统的整体微分方程模型的矩阵形式如式（1）所示：

2 数值仿真与结果分析

为了从时域与频域两个角度分析电站尾水系统在较低水位出现的超低频振荡现象，本研究分别以电站尾水位和尾水支渠局部水力损失为控制变量，通过时域数值仿真和特征频率分析相结合的方法，分析不同因素对系统稳定性的影响。

2.1 尾水水位对系统稳定性的影响

针对电站下游水位不同时双机额定功率运行状态下系统水力动态开展时域仿真，探索尾水位变化对尾水系统中水力振荡的影响。研究选取电站尾水出口明渠水深分别为7.0m，7.5m和8.0m 的运行工况进行仿真。电站尾水位对系统超低频振荡的影响趋势如图2 所示。由图2 可知，尾水位对系统超低频振荡影响明显，假设各曲线对应工况具有完全相同的管道、渠道糙率和局部水力损失系数，尾闸室的水压振荡幅值随尾水位的升高而明显减小，说明由于电站尾水流道水力不平衡因素导致的机组有功功率波动现象只存在于部分运行工况，且与下游河道的尾水位密切相关，尾水位较低时易出现振荡现象。

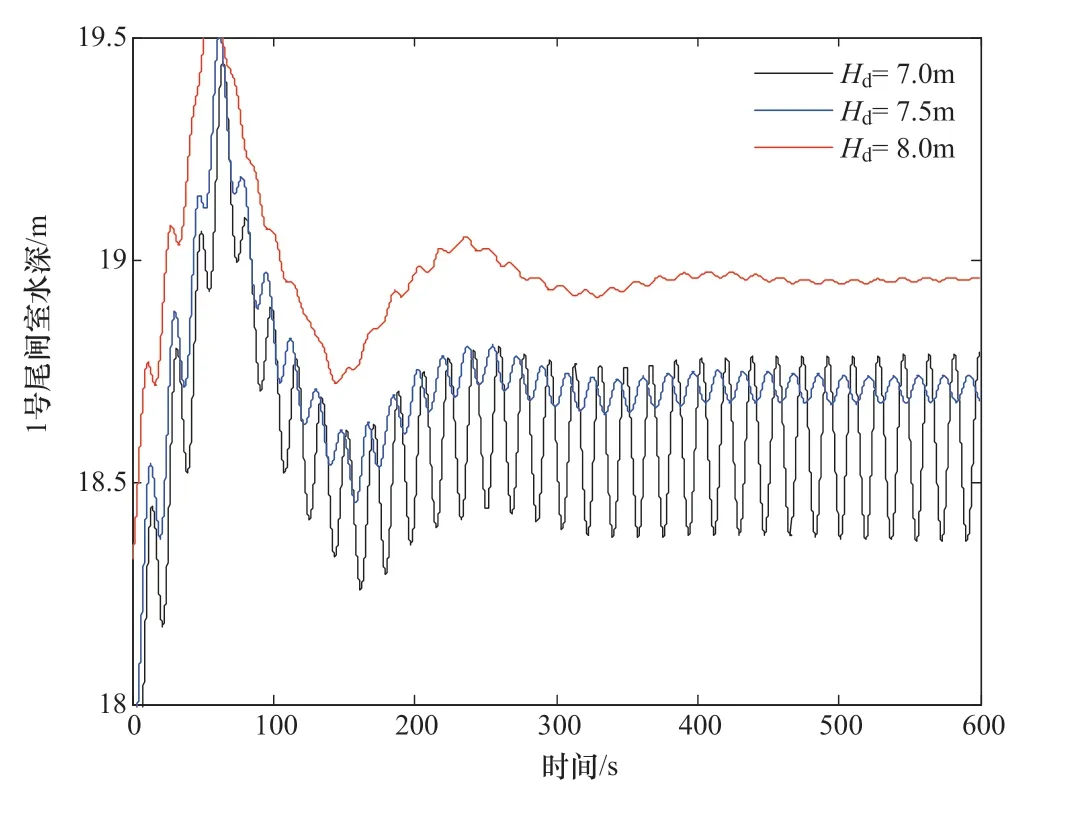
图2 不同电站下游水位时尾闸室水深时域仿真曲线Figure 2 Curves of the water depth at the tailrace gate chamber at different tailrace levels

状态方程系统矩阵的特征值可用于判断系统稳定性：特征值的实部代表振荡的衰减因子，当特征值实部均分布在复平面左半平面时，系统趋于稳定。特征值的虚部代表系统的特征频率，相应的特征向量表示振型。由于针对电站尾水系统所建立的状态空间方程形式数学模型属于非定常参数状态空间方程模型，在动态过程中模型的参数矩阵A、B、C随系统状态不断变化。因此，用系统某一平衡点处的线性化定常参数模型进行特征值分析难以完全描述系统稳定性表现，研究采用变参数模型计算尾水系统在各采样时刻的特征值，并统计整个动态过程中特征值分布轨迹能够更直观地观察系统稳定性。

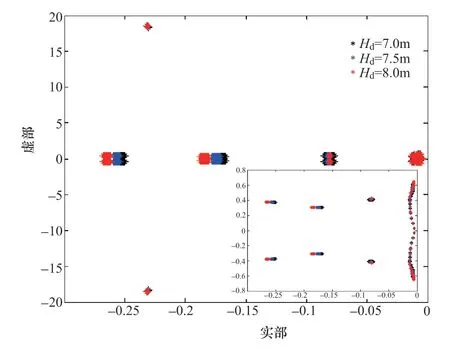
图3 不同电站下游水位时尾水系统特征值分布Figure 3 Eigenvalue distribution of the system at different tailrace levels

2.2 局部水力损失对系统稳定性的影响

为探究水电站低尾水位工况下运行时的抑制或消除上述水力振荡的有效方法，研究以尾水水深Hd=7.0m 工况为例，分别对尾水支渠上增加不同大小的局部水力损失的系统水力动态进行时域仿真，分析尾水水力振荡与尾水流道局部水力损失之间的关系。对比两段尾水支渠在原始系统仿真参数设置条件下以及同时将两支渠局部水力损失系数分别增加Δη1=0.340 和Δη2=0.605两种情况对应的尾闸室水深动态过程时域曲线如图4 所示。

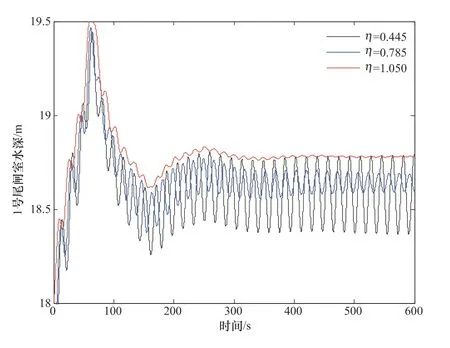
图4 不同尾水支渠局部水力损失时尾闸室水深时域仿真曲线Figure 4 Curves of the water depth at the tailrace gate chamber with different local hydraulic losses on the branch channels

由图4 可知，通过在两支渠上同时增加水力损失可以达到抑制尾水系统水力周期性振荡的效果，当局部水力损失系数增量达到Δη2时，尾闸室处水力振荡基本消失。

进一步分析不同尾水支渠水力损失系数条件下尾水系统的特征值分布情况，如图5 所示。从图中可以看出，与第2.1节的特征值分析结果相类似，三种不同尾水支渠局部水力损失系数条件下，尾水系统各阶特征值的虚部基本保持一致，并且随着支渠局部水力损失系数的增大，特征值实部距离复平面纵轴的水平距离随之增大，振荡衰减速度更快，说明工程中有望通过提高尾水支渠处对应的局部水力损失的相关方案来实现该类低频振荡的抑制甚至消除。

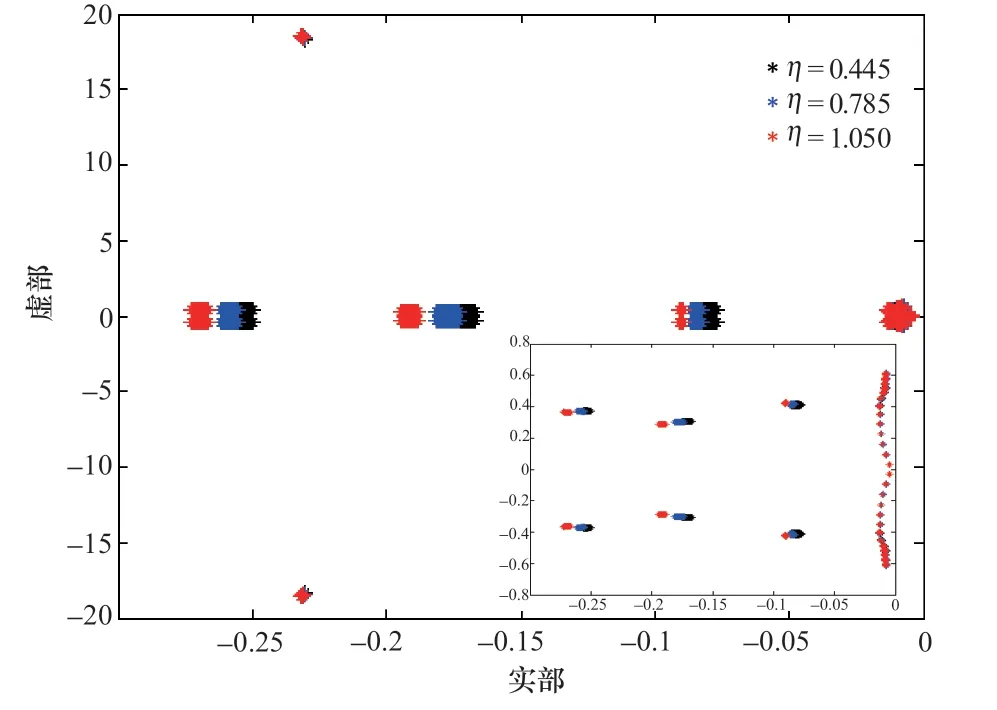
图5 不同尾水支渠局部水力损失时尾水系统特征值分布Figure 5 Eigenvalue distribution of the system with different local hydraulic losses on the branch channels

3 结束语

本文采取电路等效法建立了电站明满流尾水系统高阶数学模型，在所建模型基础上分别开展了不同尾水位和不同尾水支渠局部水力损失状态下的系统时域仿真，探索关键节点处水力波动的变化规律，并对系统进行特征频率分析，分析系统稳定性变化规律，寻求抑制超低频振荡的合理解决方案。