河段挟沙力计算方法及其在黄河下游的应用

夏军强，戈向阳，周美蓉

（1.武汉大学水资源工程与调度全国重点实验室，湖北武汉 430072；2.水利部牧区水利科学研究所，内蒙古呼和浩特 010020）

0 引言

小浪底水库蓄水拦沙运用改变了黄河下游的径流过程，清水下泄使得下游发生剧烈的冲刷［1-2］，河道断面形态趋向窄深［3-4］，对黄河下游水流挟沙力及河道输沙能力产生了很大影响。 研究黄河下游近期水流挟沙力的时空变化特点，对于确定黄河下游河槽排洪输沙基本功能和水沙调控指标具有重要意义。

水流挟沙力作为泥沙基本理论研究的一个传统课题，是指河道冲淤平衡状态下单位水流挟带泥沙的能力，其变化是研究悬沙输移及河道演变的核心问题之一。 国外最早关于水流挟沙力的研究始于Gilbert等［5］的水槽输沙试验；我国水流挟沙力研究于1947年［6］开始，1954 年南京水利实验处进行了人工沙饱和悬沙试验，并根据试验数据得到水流挟沙力经验关系式［7］。 截至目前，国内外学者关于水流挟沙力已提出大量经验半经验公式，其中具有代表性的有Einstein公式［8］、张瑞瑾公式［9］、Bagnold 公式［10］、窦国仁公式［11］、张红武公式［12］、韩其为公式［13］等。 其中，张红武等［12］认为泥沙悬浮能量来自水流运动动能、水流能量消耗和泥沙悬浮功，且这三者之间必定存在着内在联系，并考虑到卡门常数和泥沙沉速等会受泥沙存在的影响，提出了一个半经验半理论的水流挟沙力公式（业内称为张红武公式）。 大量研究证明张红武公式在计算高含沙水流挟沙力时具有较高精度［14-15］。 然而目前水流挟沙力公式大多只能计算典型断面的挟沙力，用于反映整个河段的情况［16-18］。 如：刘继祥［16］选取黄河中下游干支流14 个水文站，研究了黄河下游的水流挟沙力及其影响因素；要威等［17］基于黄河下游游荡段花园口—高村河段的水沙资料，得出了适用于断面形态变幅大的游荡段的挟沙力沿河宽分布的公式；Xia 等［18］根据黄河下游8 个水文站的实测挟沙力资料，验证了张红武公式中参数取值的准确性。 但特定断面的水流挟沙力调整情况无法代表整个河段。

因此，本文基于实测水沙和地形资料，提出了一种河段水流挟沙力的计算方法，分析了1986—2020 年黄河下游游荡段、过渡段、弯曲段河段挟沙力的时空变化特点。

1 河段挟沙力的定义及计算方法

1.1 河段挟沙力定义

黄河下游河床形态沿程变化剧烈，实测水文断面分布不均，河段内某一特定断面的挟沙力难以代表整个河段的挟沙能力。 因此，需要结合河段尺度的河床形态参数，提出河段挟沙力的计算方法。 首先进行河道概化，综合考虑河段内各个断面的形态和流量，以及相邻断面间距不等的实际情况，提出一个理想的河段平均化的断面（见图1，图中Q、S、A、H分别为流量、含沙量、断面面积、水深）。 然后提出河段挟沙力的定义：在河段平均的水流和泥沙综合条件下，能够通过河段下泄的临界含沙量。 当水流中含沙量超过这一数值时，河段将发生河床淤积；反之，河段将发生河床冲刷。

图1 河道概化

1.2 河段挟沙力计算方法

张红武公式应用广泛，在计算高含沙水流和低含沙水流的挟沙力时均具有较高的精度，因此本文将其作为推导河段平均挟沙力的基础公式，具体形式如下［12］：

式中：U为流速，H为水深，g为重力加速度，ωm为非均匀悬沙的平均沉速，Sv为体积比含沙量，γs和γm分别为泥沙容重和浑水容重，κ为浑水的卡门常数，D50为床沙的中值粒径，k为系数，m为指数。

选定了挟沙力公式后，要对公式中的参数进行河段平均化处理，主要包括河道水力几何参数的河段平均化以及泥沙参数的计算。

1.2.1水力几何参数的河段平均化

河段平均流量与过水断面面积采用Xia 等［19］提出的基于对数变换的几何平均与断面间距加权平均结合的方法来计算，可保证河道形态的连续性，即存在为平均河宽，为平均水深）。 具体步骤如下：首先采用一维水沙数学模型［20］计算出各统测断面不同流量对应的水位；然后根据各断面的水位流量关系，确定汛期平均流量对应的水位，从而计算出相应的过水断面面积、河宽、水深；最后采用式（3）计算河段平均值。

1.2.2泥沙参数计算

水流挟沙力公式中需要平均化的泥沙参数包括Sv、γm、ωm等。 其中体积比含沙量的转换公式为Sv＝S／ρs（S为含沙量，ρs为泥沙的天然密度，取2 650 kg／m3），浑水容重的计算式为γm＝ρmg＝［ρ水（1-Sv）+ρ沙Sv］g，浑水的卡门常数与清水的卡门常数κ0＝0.4 的关系为本文采用河段内各水文断面泥沙参数的算术平均值作为河段平均的泥沙参数值。 此外，非均匀悬沙平均沉速（ωm）采用韩其为［21］方法计算：

式中：N为挟沙力分组数；pi为挟沙力级配，可以用李义天［22］方法确定；n为待确定量，根据以往研究成果取为第i粒径组泥沙的群体沉速，其中d50为悬沙中值粒径，ωi为第i粒径组泥沙在清水中的沉速，这里采用张瑞瑾泥沙沉速公式［9］进行计算。

通常认为黄河下游悬沙粒径小于0.025 mm 的细沙为冲泻质，不参与造床作用，故计算悬沙平均沉速时不考虑冲泻质组分。

1.2.3挟沙力公式参数率定

经过水力几何参数的河段平均化以及泥沙参数计算，张红武公式可转换为如下形式：

定义水沙综合参数：

将河段平均水力几何参数与泥沙参数代入后即可得到黄河下游各河段1986—2020 年逐年的水沙综合参数，如图2 所示。 游荡段水沙综合参数的取值为0.07～49.66，小浪底水库运用前多年平均值为28.27，小浪底水库运用后减小至1.46；过渡段水沙综合参数的取值为0.12 ～68.48，多年平均值由小浪底水库运用前的32.62 减小至小浪底水库运用后的2.38；弯曲段水沙综合参数的取值为0.14 ～63.59，多年平均值由小浪底水库运用前的27.45 减小至小浪底水库运用后的2.73。

图2 黄河下游各河段水沙综合参数逐年变化情况

张瑞瑾［9］的研究结果表明，挟沙力公式的系数k和指数m随水沙综合参数变化而变化。 当公式中的水沙参数拓展到河段平均的形式后，有必要重新率定张红武公式中的系数k和指数m，使之更准确地反映河段水沙条件下的水流挟沙力。 本文从一维河流数学模型基本控制方程组中的河床变形方程入手，通过年度实测冲淤量倒推计算河段挟沙力；接着拟合各河段水沙综合参数与挟沙力计算值的幂函数关系，即可得到河段挟沙力公式中的系数k和指数m。河床变形方程：

经过公式变换得到S*的表达式为

式中：A0为河床总冲淤断面面积，t为时间，ρ'为床沙干密度，ωm为悬沙沉速，α为恢复饱和系数（采用韩其为［23］在研究非均匀悬移质不平衡输沙时提出的方法，当河床淤积时α＝0.25，河床冲刷时α＝1.0）。

2 黄河下游河段挟沙力计算结果

2.1 研究河段概况

研究河段干流全长756 km，总落差94 m，流域面积2.3 万km2，占黄河总流域面积的3%。 河段内大量泥沙落淤，部分河段形成了举世闻名的地上“悬河”。黄河下游按照河道形态及河床演变特点可分为游荡段、过渡段、弯曲段［24］，如图3 所示，沿程有花园口、夹河滩、高村等7 个水文站。 总体来说，黄河下游河道具有上宽下窄、上陡下缓、上段冲淤变化大、下段较为稳定等特点。 游荡段全长299 km，河道比较顺直，具有水流宽浅散乱、主流摆动不定、河势变化剧烈等演变特点。 过渡段长约185 km，该河段区间无支流入汇，平滩河槽相对较窄，河段内有大量河道整治工程，河势基本得到控制。 弯曲段长约272 km，沿岸设有大量的险工和控导工程，防护长度占该河段总长的70%以上［25］，主槽形态较为窄深，滩槽高差较大。

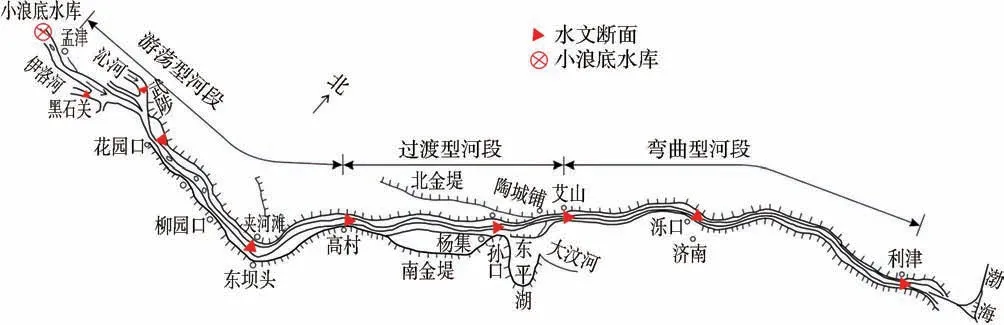
图3 黄河下游河道示意

黄河下游的水沙来源主要是三门峡以上干流、三门峡至花园口区间。 图4（a）点绘了1986—2020 年进入黄河下游的水沙变化过程。 小浪底水库运用前（1986—1999 年）黄河下游的年均水量为279 亿m3，年均沙量为6.9 亿t。 小浪底水库运用后，受中上游水土保持、水库蓄水拦沙、水沙联合调度等因素影响，黄河下游年均水量为277 亿m3，年均沙量显著减小至1.0亿t，较1986—1999 年减小了85%。 此外，来水量年内分配发生变化，非汛期来水量占比增大，1986—1999 年非汛期来水量占全年的53%，而2000—2020年提升至60%；来沙量大幅度减少，2000—2020 年年均来沙量仅为1986—1999 年的15%，且来沙集中在汛期，占全年的80%。

图4 黄河下游水沙条件及累计冲淤量变化情况

小浪底水库运用前，进入黄河下游的水少沙多，水沙关系严重不协调，河床长期处于淤积状态，但是在一些有利的水沙条件下，也会出现河床冲刷［26］；小浪底水库运用后，黄河下游处于持续冲刷状态。 图4（b）为黄河下游各河段的河床累计冲淤过程。 1986—1999年，受龙羊峡水库建成运用以及降雨等因素的影响，黄河下游枯水历时增加，河流输沙动力不足，导致下游基本处于持续淤积的状态，下游累计淤积量为21 亿m3。小浪底水库蓄水拦沙运用后（2000—2020 年），来沙量减少使得下游转为剧烈冲刷状态。 2000—2020 年黄河下游总冲刷量为20 亿m3，从冲刷的沿程分布来看，高村以上游荡段的冲刷量达13.38 亿m3，占下游总冲刷量的67%，过渡段和弯曲段的冲刷量相当，分别占17%和16%，表现为上段冲刷幅度大、中段与下段冲刷幅度小的特点［27］。

黄河下游河道的持续冲刷，一方面使沿程各河段床面发生不同程度的粗化，中值粒径基本在0.05 mm 以上，且粗化程度沿程减弱；另一方面使得黄河下游河床横断面形态发生了显著调整，改变了小浪底水库运用前黄河下游河槽逐渐萎缩的情况。 小浪底水库运用后，各河段平滩断面面积逐年增大且平滩水深持续增加，从而使得河相系数持续减小，其中：游荡段的减小幅度最大，2020 年汛后河相系数比1999 年减小44%；过渡段和弯曲段的河相系数基本稳定在5.5 m-1／2和4.0 m-1／2。 上述水沙及河床边界条件的变化，均会引起水流挟沙力的调整。

2.2 河段挟沙力计算结果

2.2.1水力几何参数与泥沙参数计算结果

1986—2020 年黄河下游游荡段、过渡段、弯曲段河段平均过水断面面积年际变幅较大，而平均水深在小浪底水库运用后显著增大。 河段平均过水断面面积在游荡段、过渡段、弯曲段的取值分别为481 ～2 130 m2、422～2 018 m2、375～1 471 m2；平均水深的变化范围分别是0.68 ～2.25 m、1.10 ～3.71 m、1.48 ～4.12 m。游荡段平均流量的变化范围为375 ～2 505 m3／s，过渡段为289～2 417 m3／s，弯曲段为204～2 396 m3／s；游荡段平均流速的变化范围为0.68 ～1.75 m／s，过渡段为0.67～1.99 m／s，弯曲段为0.54～1.97 m／s。

小浪底水库运用后，黄河下游含沙量较小浪底水库运用前大幅度减小。 游荡段各水文断面平均含沙量由16.98～63.56 kg／m3减小到0.47 ～19.77 kg／m3、过渡段由14.68～46.89 kg／m3减小到0.89～19.72 kg／m3，弯曲段由10.89 ～47.56 kg／m3减小到0.89 ～21.41 kg／m3。1986—2020 年3 个河段的体积比含沙量范围分别为0.000 2～0.024 0、0.000 3～0.017 7、0.000 3～0.017 9；非均匀悬沙群体沉速范围分别为0.001 8 ～0.008 2 cm／s、0.001 4～0.005 6 cm／s、0.001 2 ～0.004 5 cm／s；浑水卡门常数的取值在0.31～0.39 之间。

2.2.2挟沙力公式率定结果

1986—2020 年黄河下游游荡段、过渡段、弯曲段汛期冲淤量分别为-1.44 亿～5.59 亿m3、-0.42 亿～0.55亿m3、-0.62 亿～0.10 亿m3。 取河床总冲淤断面面积A0为河段汛期冲淤量与河长的比值，时间t为汛期总时长，含沙量S为河段内所有水文断面含沙量的算术平均值，代入式（7），计算出游荡段、过渡段、弯曲段的挟沙力分别为0. 24 ～27. 03 kg／m3、0. 57 ～19.38 kg／m3、0.55～19.01 kg／m3。 各河段水沙综合参数与挟沙力计算值的幂函数关系见图5。

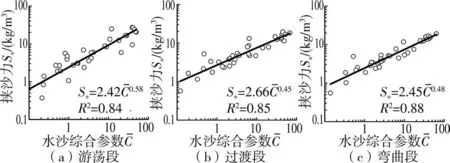
图5 黄河下游各河段水沙综合参数与挟沙力计算值的关系

由图5 可以看出，黄河下游游荡段、过渡段、弯曲段水沙综合参数与挟沙力计算值的相关程度总体较高，拟合的幂函数关系决定系数分别为0.84、0.85、0.88。 直线斜率即为挟沙力公式的指数，游荡段、过渡段、弯曲段指数m分别为0.58、0.45、0.48，进一步得到系数k分别为2.42、2.66、2.45。 结果较为合理，大致接近张红武公式k＝2.5、m＝0.62 的取值。 采用各河段拟合的幂函数公式可以计算出黄河下游各河段的水流挟沙力。 3 个河段的河段挟沙力取值为0.53 ～23.81 kg／m3、1.02～17.86 kg／m3、0.94 ～18.24 kg／m3，其综合表示了在河段平均水沙条件下水流挟沙力的大小，采用河段挟沙力计算方法得到的结果在数值上合理。

2.3 河段挟沙力时空变化特点

2.3.1河段挟沙力随时间变化特点

图6给出了黄河下游游荡段、过渡段、弯曲段河段挟沙力逐年变化情况。 1986—1999 年游荡段河段挟沙力的范围为8.24～24.00 kg／m3，平均值为16.57 kg／m3；而小浪底水库运用后，黄河下游游荡段河段挟沙力大幅度减小，减小至0.52 ～5.57 kg／m3，多年平均值为2.73 kg／m3，较运用前减小了84%。 过渡段河段挟沙力范围由小浪底水库运用前的4.54 ～17.74 kg／m3减小至运用后的1.03 ～6.21 kg／m3，多年平均值由12.00 kg／m3减小至3.52 kg／m3，减小了约71%。 弯曲段河段挟沙力由小浪底水库运用前的3.05～18.34 kg／m3（多年平均值为11.33 kg／m3）减小至0.94～7.46 kg／m3（多年平均值为3.52 kg／m3），减小了69%。 3 个河段的河段挟沙力大致呈现出小浪底水库运用前逐年波动变化较大，小浪底水库运用后显著减小且逐年波动幅度也减小的变化特点。

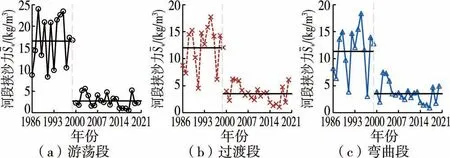
图6 黄河下游河段挟沙力逐年变化情况

对黄河下游游荡段、过渡段、弯曲段河段挟沙力的时间变化序列，进行Mann-Kendall 趋势检验和Mann-Kendall 突变检验，分析河段挟沙力的变化趋势及突变态势。 研究时段内，黄河下游游荡段、过渡段、弯曲段的β值均小于0，且｜Z｜≥2.58，通过了1%显著性检验，这表明各河段挟沙力在99%的置信区间内呈现显著性减小趋势。 经突变检验，在置信水平0.01 的基础上，游荡段、过渡段、弯曲段河段挟沙力的M-K 统计值由正值转为负值的年份均发生在1999 年。 这是因为1999 年小浪底水库运用，水库的蓄水拦沙作用导致进入黄河下游的水沙条件发生显著改变，进而导致下游各河段挟沙力转变为持续减小的状态。

2.3.2河段挟沙力沿程变化特点

小浪底水库运用前，河段挟沙力平均值大致呈沿程减小的趋势，在游荡段、过渡段、弯曲段分别为16.57、12.00、11.33 kg／m3，沿程减小了32%。 小浪底水库运用后，河段挟沙力平均值呈沿程增大的变化规律，分别为2.73、3.52、3.52 kg／m3，沿程增大了29%。河段挟沙力明显地表现出小浪底水库运用前沿程减小、运用后沿程增大的变化特点（见图7）。

图7 黄河下游沿程河段挟沙力

小浪底水库运用前黄河下游床沙中值粒径沿程变化较小，但河段平均流速沿程先增大后减小，平均水深沿程增大（见图8），悬沙平均沉速沿程减小了32%，直接导致水沙综合参数减小了约6%，河段挟沙力沿程减小；此外，含沙量沿程减小使得体积比含沙量沿程减小，使得河段挟沙力从游荡段到过渡段减小28%，过渡段到弯曲段减小6%。 小浪底水库运用后，床沙中值粒沿程减小了35%，使得河床的可冲性沿程增大，床沙对水流中粒径较细的泥沙补给沿程增加，导致河段挟沙力沿程增大；河段平均流速沿程增大了15%，水深沿程增大了63%，悬沙沉速沿程减小幅度增大至45%。 床沙中值粒径、河段平均流速与悬沙沉速这3个因素的变化共同使得水沙综合参数增大了69%，导致河段挟沙力沿程增大。

图8 黄河下游各河段水力要素沿程变化

3 结论

黄河下游河床形态沿程变化很大且实测水文断面分布不均匀，采用断面数据计算得到的挟沙力仅能反映特定水文断面的挟沙能力，因此需要将以往断面挟沙力的计算方法拓展到河段尺度。 本文的主要结论如下。

1）提出了一种河段水流挟沙力的计算方法。 该方法首先基于1986—2020 年黄河下游7 个水文断面的汛后地形资料及日均水沙资料，计算河段平均水沙综合参数。 再根据挟沙力计算值与水沙综合参数的相关关系，重新率定在河段平均水沙条件下张红武公式的指数与系数，拟合的相关关系式的决定系数均在0.84以上。 从而得到黄河下游游荡段、过渡段、弯曲段河段平均条件下挟沙力公式的系数k分别为2.42、2.66、2.45，指数m分别为0.58、0.45、0.48。

2）1986—2020 年游荡段、过渡段、弯曲段的河段挟沙力范围分别为0.52～24.00 kg／m3、1.03 ～17.74 kg／m3和0.94 ～18.34 kg／m3。 在时间上，呈现出小浪底水库运用前年际变化较大，水库运用后变化显著减小的特点，河段挟沙力较水库运用前减小69%以上。 在空间上，小浪底水库运用前河段挟沙力呈现沿程减小的变化趋势，总体减小了32%；水库运用后呈现沿程增大的变化趋势，增大了约29%。 这是由床沙沿程变细使得床沙对水流中泥沙补给变多以及河槽断面形态沿程趋于窄深共同导致的。