基于圆形条纹径向空间载波相移的三维动态测量技术

马 颖*，吴小青

（无锡南洋职业技术学院，江苏 无锡）

引言

随着对三维动态测量的需求不断增加，各种快速相位恢复方法不断涌现[1-2]。由于傅里叶变换方法只需要一个条纹图案来求解相位轮廓，因此它引起了研究人员的注意。结合多频率时间展开[3]和格雷编码[4]，以额外投影更多的图像为代价来解决相位模糊问题。

2015 年，涂颜帅[5]提出了一种基于时间频率编码的高速三维测量方案。利用高速率投影仪，在不同时间投影不同频率的编码条纹，并用较低的帧速率，将若干个不同时刻的变形条纹曝光在同一张图中。通过对图像的分析处理, 可以获得各个条纹对应的三维数据，即对应时刻的三维面形数据。由于需要大量的图案投影，此方案高速投影和高速摄像机记录至关重要。2020 年，李勇等人[6]对条纹投影动态三维表面成像技术进行了总结。介绍了动态成像，包括高速投影方案和采用速度相对低的相机进行动态三维表面成像的方案。特别是动态三维成像中绝对相位获取方法，主要是模拟和数字编码法及高精度动态相位测量法。至今，准确性和速度之间的权衡仍然是一个复杂的问题，值得进一步探讨。

本文提出了一种径向空间载波相移算法来适应圆形条纹图案，并有效地实现了动态三维测量。该算法通过捕获沿径向方向具有像素错位的条纹图案来提取两幅相移条纹图案，实现了数字径向相移。仿真和实验皆证明了该方法的有效性。

1 测量原理及步骤

根据此前对圆条纹的理论分析[7]，本文将圆条纹应用到相移上来。本文选取圆条纹右下角的部分圆弧，将其投影到被测物体上，并令采集到的变形条纹图的像素坐标为（x，y）。为了方便起见，在本文的以下叙述中，将这部分条纹统称为圆形条纹，其光强表达式为：

其中，a（x，y）为背景光强；b（x，y）为调制度；（x，y）为相机的像素坐标；φ（x，y）为相位分布。

采集投影在物体上的变形条纹，取其中一帧图像作为原始图像，原始图像记为I2（x，y）。将条纹向接近圆心的方向移动一个像素，即表现为将I2（x，y）先向左移动一个像素再向上移动一个像素，得到的光强图记为I1（x，y）；将条纹向远离圆心方向移动一个像素，定义为将原始图像先向右移动一个像素再向下移动一个像素，得到的光强图记为I3（x，y）；这样即获得新的三幅具有相移量的光强图，其光强表达式为：

其中，δx（x，y）和δy（x，y）为I1（x，y）和I3（x，y）在x、y 方向的相对相移量；Φ（x，y）为载波相位，Φ（x，y）=2π·f·r；f 为条纹频率；r 为极坐标半径。ak（x，y）为第k幅光强图的背景光强；bk（x，y）为第k 幅光强图的调制度。

由于这三幅光强图的背景光强和调制度的变化缓慢，所以参数a，b 变化基本可以忽略不计。

根据傅里叶变换方法和欧拉公式，式（2）可以表示为：

其中，Ik（x，y）表示第k 幅光强图；ck（x，y）*表示ck（x，y）的复共轭；ck（x，y）为待测物体的复振幅分布，k=1，2，3。ck（x，y）可以表示为：

其中，i 为单位虚数；φk为第k 幅光强图的相位分布，可表示为：

取第一和第三幅光强图分别进行傅里叶变换，再利用一个低通滤波器，得到+1 阶频谱，并将频谱移到中心。然后进行逆傅里叶变换，并对c1（x，y）和c3（x，y）直接进行了减法运算：

根据欧拉公式，可以得到：

两式相除得到：

即:

其中，w 为包裹算子。

由于φ1，φ2，与φ3之间仅存在约一个像素错位，且相互联系，所以取两值平均可得：

即可得到原始图像的相位分布，即为它的包裹相位。

在快速解得包裹相位后，利用相位展开算法[8]即可获得连续相位。

根据传统的标定高度- 相位的映射关系：

获得的连续相位，通过设定多个已知高度与此高度上对应的相位差即可解得标定参数，结合相机标定参数，从而得到物体的三维轮廓信息。

2 模拟仿真

通过模拟仿真验证该方法的可行性。图1(a)是一幅512×512 像素的圆条纹图，频率为0.156 Hz。函数“peaks”是MATLAB 中内置的实例函数，本文将圆形条纹图加载至此函数上，此时图像被函数“peaks”调制，产生带有峰值轮廓信息的变形条纹。根据本文提出的方法，计算得到图1(b)为最终计算得到的相位值，如图1(b)所示，与原始峰值图基本一致。

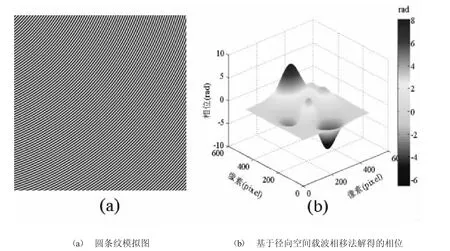
图1

3 实验验证

本文实验以电灯灯罩为待测物体，并保持灯罩上下移动，构成动态待测物体。期间连续采集投影在此物体上的变形条纹，同时处理成一帧帧的图像；取其中一帧帧图像作为原始图像，按照以上算法，测量算法在动态场景下的适用性。本文选择4 个不同位置的图像作为测量样本（分别对应于第1 帧，第79 帧和第136 帧图像）。图2（a）- 图2（d）为上述四个位置处采集到的变形条纹图像；图2（e）- 图2（h）为对应这4 个位置的三维测量结果。由图可见，此物体的面型轮廓得到了很好的恢复。

图2

4 结论

本文提出了一种利用径向空间载波相移算法实现动态三维测量的方法。它从捕获的具有径向像素错位的圆形条纹图像中获取三个相移条纹图案，从而实现了数字上的径向相移。此外，仿真和实验证明了本文方法的有效性，该方法具有较低的相位误差和较高的精度，并以较高的效率成功地实现了三维动态测量。