基于CODAS的CBTC车载系统子系统故障风险评估与维修优先级决策方法

王宗耀，上官伟，2，彭 聪，师泽斌

(1.北京交通大学 电子信息工程学院，北京 100044；2.北京交通大学 轨道交通控制与安全国家重点实验室，北京 100044)

我国城市轨道交通系统当前正处于快速发展阶段。城市轨道交通的安全高效运行离不开基于通信的列车控制系统(Communication Based Train Control System,CBTC)的支持,CBTC是一种旨在保证城市轨道交通线路安全高效运行,以列车自动防护为核心的系统,其下属每个子系统都是保证系统可靠性的重要基础。其中,CBTC车载系统是CBTC中最重要的子系统,为实现列车超速保护、自动驾驶和人机交互提供了安全可靠的保障,CBTC车载系统的基本结构见图1。对CBTC车载系统按子系统进行划分,主要可分为列车自动防护(Automatic Train Protection, ATP)、列车自动驾驶(Automatic Train Operation, ATO)、数据通信系统(Data Communication System, DCS)、人机接口(Man Machine Interface, MMI)、应合器传输模块(Balise Transmission Module, BTM)等子系统。城市轨道交通系统的高可靠性离不开预先的故障风险评估与科学、及时的维修策略。风险表示故障发生的可能性及其可能带来的危害性后果,故障风险评估是依据建立的故障风险指标评价体系,对故障风险进行定性分析的有力策略。基于故障风险评估结果,结合平均维修时间的维修优先级决策,更是预防灾害性结果与指导视情维修的重要前提。深入挖掘故障间隔时间不同尺度下的分布情况,建立科学、细粒度的决策指标体系,并客观地进行子系统故障风险评估与维修优先级决策,是保证城市轨道交通高可靠、高效率、高稳定运行的理论基础,也是保证乘客与相关技术人员生命安全不容忽视的前提条件。

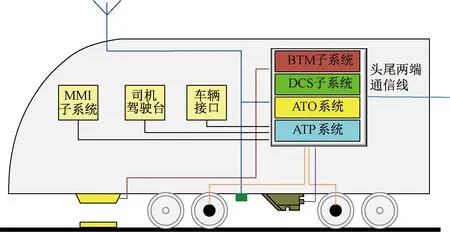
图1 CBTC车载系统基本结构

依托故障间隔时间,建立合理的故障评价指标是实现故障风险评估的基础。文献[1]引入数据空间模型概念,分别建立列控车载子系统物理空间特征数据模型和时间特征数据模型,并结合威布尔分布设计一种基于时空特性分析的可靠性分析算法,对典型系统及设备可靠性进行分析。子系统故障重要度评价指标是基于故障间隔时间的分布情况所提出的表征子系统发生故障及故障引起系统故障的可能性的大小。文献[2]通过正、反向推理分析铁路危险货物运输过程中各事件的结构重要度、概率重要度、关键重要度,采用基于三位一体的重要度评价并对此进行排序,定量地刻画出运输过程的风险性,同时找出需重点关注的工作环节,并针对性地提出改进措施。文献[3]中对电力系统抗风灾结构设备建立了风灾条件下的故障率模型,通过求解顺序维修模型并进行充分的重采样后得到部件修复力矩的分布函数,并采用Copeland排序法对部件重要性进行排序。同时,还有部分学者在其他领域结合重要度进行了可靠性评估[4-5]。

故障风险评估是基于多维决策理论在可靠性方面的具体应用,其目的是在多维评价指标体系下确定不同设备的危险等级。文献[6]针对影响铁路货运量因素较多的问题,采用灰色关联分析作为分析系统的方法,结合LS-SVM对铁路货运量进行预测。文献[7]基于理想解相似度排序技术评估可持续供应链风险管理,结合准则相关性重要度对电信设备的好坏程度进行排名。文献[8]提出一种基于云模型理论和基于理想点法的集成故障模式和影响分析模型,利用主观权重计算方法计算初始权重,并利用云分层与理想点法确定故障模式的风险优先级。

评估子系统维修优先级别、确定系统中各组件维修顺序是制定高效的视情维修策略的理论基础。文献[9]考虑了维护等待时间与维修优先级优化了风电机组的预防性维修策略。文献[10]提出一种基于rankboost的数据驱动断路器的维护优先级确定方法,通过设备级状态监测参数与系统级可靠性指标确定维修权重,比单一依靠监测参数与可靠性指标得到的维修优先级更具有现实意义,在农业[11]、建筑[12]、机械[13]及其他行业[14-16]都取得了一定的研究成果。

充分挖掘文本数据与系统可靠性间的关联,提出合理健全的故障风险评价指标,采用最优多维决策战略,是进行故障分析评估的关键。然而,目前针对故障文本数据挖掘与利用仍停留在故障机理分析、故障诊断等浅层环节[17]。与此同时,故障风险评估未完全突破基于“原始指标”“主观性强”与“低灵敏度多维决策”的传统风险评估方式。当前针对基于故障风险的维修优先级决策研究不够深入,维修优先级指标分析不全面,严重依赖于“维修数据”等历史维护信息。因此,在基于调研文献的基础上,本文以CBTC车载系统及其子系统为研究对象,将故障发生概率[18]、故障影响度[18]、故障严重度[19]考虑为故障风险评估体系建立的基本属性,从不确定性、可变性与危害性三方面诠释风险的本质[20],结合CBTC车载系统实际运维数据,针对CBTC车载系统及其子系统建立了细粒度的故障风险评估指标体系。按故障发生频次将车载系统划分为不同类别的子系统,首先对故障间隔时间进行拟合,并利用K-S检验法选择最优的分布模型;然后,采用最优分布模型深入挖掘故障间隔时间在时间尺度上的分布情况,建立相应的可靠度模型,基于弗雷歇距离衡量子系统与系统间的曲线相似度,建立以可靠性影响度、逆平均利用率、故障发生度与故障发生紧急程度为基础的故障风险评价指标体系,并基于此构建CBTC车载系统子系统的故障风险评估模型,采用熵权法结合距离的评估方式,实现对子系统故障风险的评估;同时,以故障风险评估过程中求解的欧式距离、出租车距离与历史平均维修时间作为确定维修优先等级的决策指标,建立子系统维修优先度的熵权法-CODAS模型,为制定科学的检修策略提供参考。本文所提方法的基本流程见图2。

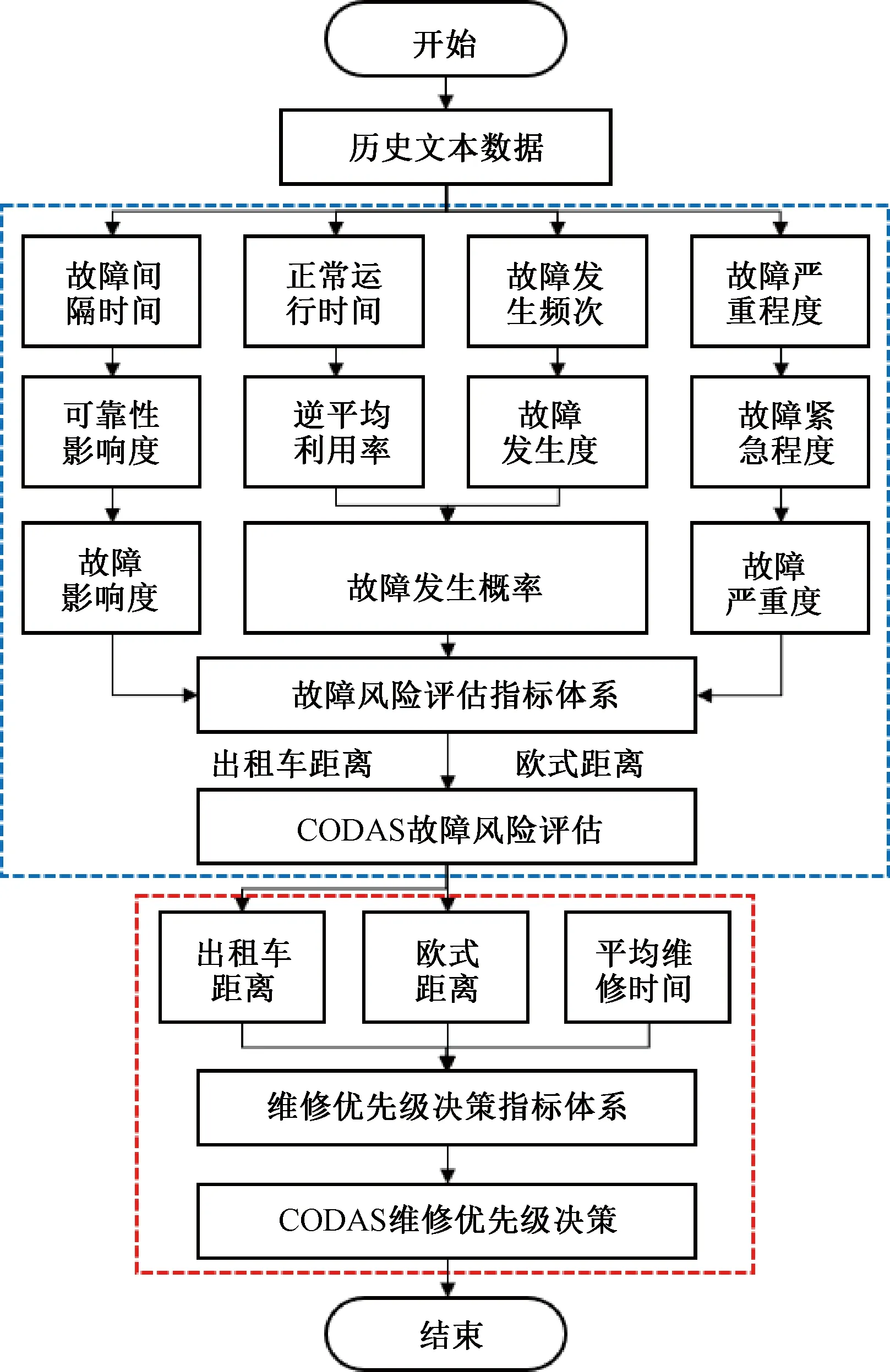
图2 CBTC子系统故障风险评估与维修优先级决策流程图

1 基于曲线相似度的CBTC车载系统及其子系统可靠性影响度评价

1.1 基于分布模型选择的CBTC车载系统及其子系统可靠性评估方法

确立CBTC车载系统及子系统可靠性参数的分布函数,是进行可靠性评估的首要基础。对于轨道交通系统或设备,通常采用对数正态分布或双参数威布尔分布(以下简称威布尔分布)拟合其故障间隔时间的分布情况[21-22]。因此,本文以对数正态分布与威布尔分布作为CBTC车载系统及其子系统故障间隔时间的假设分布模型,并利用K-S检验法选择最优分布模型以求解系统的可靠度函数。

对数正态分布与威布尔分布的概率密度函数为

( 1 )

( 2 )

式中:x为CBTC车载系统故障间隔时间;μ和σ分别为对数正态分布的平均值与标准差;η和β分别为威布尔分布的形状参数与尺度参数。对数正态分布与威布尔分布的累积分布函数为

( 3 )

( 4 )

若故障间隔时间xi服从对数正态分布,令yi=lnxi,则对数正态分布的似然函数为

( 5 )

威布尔分布的似然函数为

L(η,β)=-ηnlnβ+nlnη+

( 6 )

利用极大似然估计,即可求得对数正态分布参数μ与σ、威布尔分布参数η与β的值。

为了验证分布模型的可信度,利用K-S检验法进行检验,以验证假设的分布模型的有效性。K-S检验过程为

[H,S]=kstest(data,cdf)

( 7 )

式中:H为假设检验变量,在本文中,H表示假设故障间隔时间服从某一分布,当H=0时,表示接收该假设,当H=1时,表示拒绝该假设;S为假设发生的概率,S越大,表示该假设越有概率发生;kestest为单样本Kolomogorov-Smirnov测试的测试决策;data为原始故障间隔时间数据;cdf为根据极大似然估计得到的假设的分布模型的参数求得的相应的累积分布函数。

若两种假设分布模型之间的某一个分布的H=1,则选择另一个分布作为故障间隔时间的拟合函数;若两种分布模型的假设均成立,则选择S较大的分布作为故障间隔时间的拟合函数。将选择的拟合函数记作最优分布模型,本文所提出的最优分布模型的选择流程如表1所示。

表1 最优分布模型选择流程

其中,若假设的分布模型均不满足K-S检验的结果,则利用其他常见的分布函数(如指数分布等)对故障间隔时间进行拟合,并通过K-S检验验证模型的有效性。

若故障间隔时间的最优分布模型为对数正态分布,则系统或设备的可靠度函数R(t)为

R(t)=1-Φ((ln(t)-μ)/σ)

( 8 )

式中:Φ(·)为标准正态分布的累积分布函数;t为系统或设备运行时间。

若故障间隔时间的最优分布模型为威布尔分布,则系统或设备的可靠度函数R(t)为

( 9 )

1.2 基于曲线相似度的车载系统子系统可靠性影响度评价

曲线相似度(Curve Similarity,CS)是衡量不同变量间相关性的重要评价指标,可通过计算曲线间相似度来反映子变量与全局变量的匹配程度。其中,如何选定合适的相似度度量函数是计算曲线相似度的重要基础。本文选取弗雷歇距离作为相似度度量函数,相比传统的Hausdorff距离,弗雷歇距离同时考虑了曲线在时间和空间上的顺序,在曲线相似度计算领域有着广泛的应用[23-24]。

弗雷歇距离是法国数学家弗雷歇通过观察人-狗模型提出的衡量两条曲线相似程度的距离。由于连续曲线的距离难以计算,文献[25]提出了离散弗雷歇距离的概念,以离散曲线拟合连续曲线的变化,两曲线间弗雷歇距离越小,其相似性越高。

给定两条离散曲线,u={u1,…,ui,…,um},y={y1,…,yj,…,yn},计算两条曲线点之间的欧式距离,得到m×n矩阵为

(10)

假设从d11到dmn之间存在c条路径,设W={w1,…,wk,…,wc},以路径wk为例,每段路径覆盖的两曲线间欧式距离值的个数记为nk,定义Lk,nk={L1,…,L2,…,Lnk}且定义其集合为

Lk={Lk,n1,…,Lk,nk,…,Lk,nc}

(11)

同时规定,路径必须始于d11终于dmn。

此外,规定路径需沿距离矩阵右下或右与下方向行进,见图3。首先计算每条路径覆盖的最大距离,其次在覆盖范围最大的路径中找到最小距离即为弗雷歇距离,因此定义离散曲线间的弗雷歇距离为

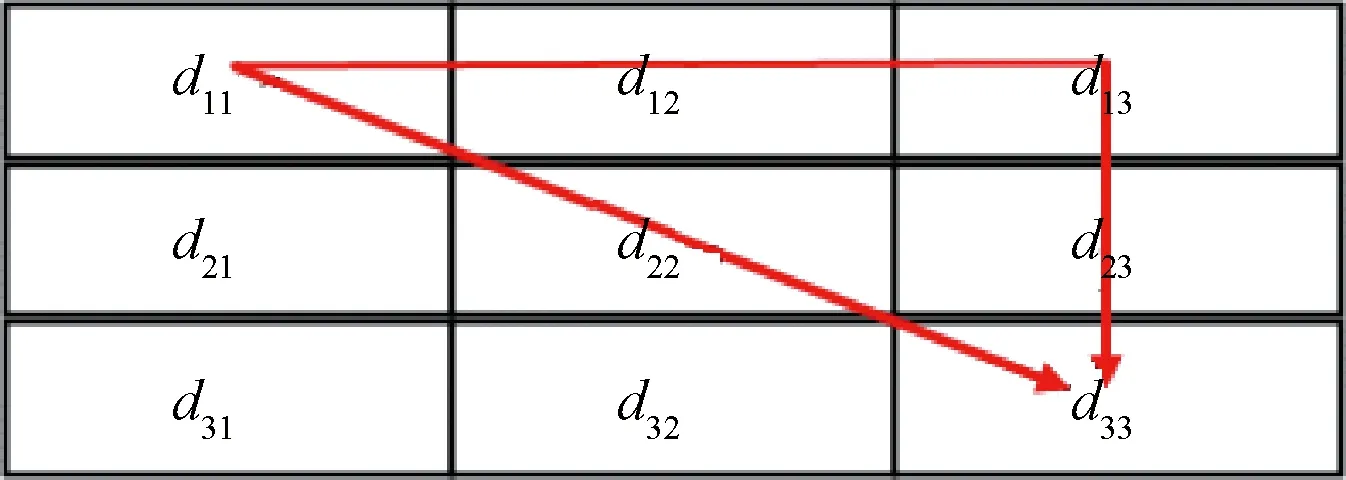
图3 弗雷歇距离路径轨迹图

F(u,y)=min{max(Lk)}

(12)

车载系统子系统对CBTC车载系统可靠性的影响程度,简称可靠性影响度,用于定量表征子系统的可靠情况与系统间可靠度演化趋势的权重关系,曲线相似度为可靠性影响度的评价提供了良好的理论基础。设系统可靠性曲线为l0,则子系统i的可靠度曲线li与l0间曲线相似度的计算式为

(13)

式中:Frechet(·)表示两条曲线间的弗雷歇距离。

曲线相似度能够度量子变量与全局变量的相关程度,同时可以识别出子变量对于全局变量的影响程度,即子变量与全局变量的曲线相似度越大,子变量对于全局变量的影响程度越高,为重要影响因子。对于CBTC车载系统及其子系统,子系统的可靠度曲线与车载系统的可靠度曲线越相似,说明车载系统的可靠性由子系统可靠性主导的可能性越大、该子系统发生故障时系统发生故障的可能性也越大。设CBTC车载系统为全局变量,其下属各子系统为子变量,其与全局变量的曲线相似度记作CSi。可靠性影响度表示子变量可靠性的变化对全局变量可靠性变化的影响情况,子变量的可靠性影响度越高,当子变量可靠性发生劣化时,全局变量的可靠性也会随之发生较大改变,定义车载系统子系统的可靠性影响度为

(14)

式中:k为子系统的个数。

2 基于CODAS的CBTC车载系统子系统故障风险评估与维修优先级决策

2.1 CBTC车载系统子系统逆平均利用率

由于城市轨道交通线路通常装配有多辆列车,每辆列车均装配同一类型的系统,但其中子系统的具体可靠性指标均有所差异。与此同时,每一子系统均记录有投入运营时间与故障发生时间,本节以获取的实际数据为依据,定义FAij为无故障运行时间,其数值大小为故障发生时间与投入运营时间的差值,其中,i为子系统的种类数,j为每类子系统发生故障的次数,j=1,2,3,…。定义子系统的平均利用率uri为

(15)

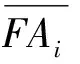
(16)

式(16)的值越大,表明此类子系统的平均利用率越低。

2.2 CBTC车载系统子系统故障发生度

为了表征子系统故障发生的频率,定义第i类子系统的故障发生度λi为

(17)

2.3 CBTC车载系统子系统故障发生紧急程度

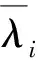
(18)

式中:occi为车载子系统i发生故障的次数;occ0为整个系统发生故障的次数。

定义子系统i的j′级故障处理优先级故障发生紧急程度Edij′为

(19)

式中:j′=1,2,3,其中,1为一般紧急,2为紧急,3为十分紧急;occij′为第i个子系统第j′级紧急程度故障发生的次数;βj′为紧急程度的条件概率,对βj′赋值为

(20)

因此,定义车载子系统i的故障发生紧急程度为

(21)

2.4 基于熵权法-CODAS的故障风险评估与维修优先级策略

2.4.1 熵权法

在故障风险评估中,权重是反映贡献度的数学参数,对于指标权重的分配是影响评估准确度的重要因素。针对模糊评价等权重分配方法无法消除其主观性的特点,本文采用熵权法对各指标分配权重。

熵权法是一种基于香农熵的权值分配方法,在相对强度度量等方面有着广泛的应用[26]。香农熵是由香农提出的、采用概率论原理的用于衡量信息间的不确定性的信息概念。

假设有i个待评价对象,每个对象有j个评价指标,定义评价集为

z={zab;a=1,2,…,i;b=1,2,…,j}

(22)

熵权法的一般步骤为

Step1为消除不确定因素对权重分配的影响,标准化评价集中每个元素zab,得到标准化后的值Pab为

(23)

Step2计算各评价指标的香农熵为

(24)

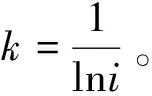
Step3计算各评价指标的发散度divb为

divb=1-Hb

(25)

Step4计算各评价指标的熵权为

(26)

2.4.2 基于熵权法-CODAS的故障风险评估与维修优先级决策

面向多评价指标的决策问题是风险评估面临的主要难点,相比于传统决策评估灵敏度较差、主观性较强的特点,本文采用一种结合距离的故障风险评估与维修优先级决策方式(CODAS)[27]。考虑故障发生重要度与故障紧急程度是表征故障风险等级的相关变量,故障风险评分与平均维修时间是表征维修优先级的特征指标。因此,本文拟采用两次熵权法-CODAS的多维决策方法对子系统分别进行故障风险评估与维修优先级决策。

相比理想点法,CODAS引入了出租车距离作为次要度量指标。基于熵权法-CODAS的故障风险评估与维修优先级决策的一般流程。

Step1根据不同子系统的不同评价指标构建决策矩阵IVm×n

(27)

式中:IVij为第i个子系统第j个评价指标的值,将不同子系统的数目记为m,将评价指标总数目记为n。

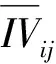
(28)

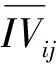
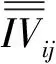
(29)

子系统各指标值与负理想解点间的距离DNPi(简称负向距离)为

(30)

Step5计算评估对象与负理想解点间的欧氏距离Ei与出租车距离Ti分别为

(31)

(32)

Step6计算各子系统间的CODAS评价值hik为

hik=(Ei-Ek)+ψ(Ei-Ek)×(Ti-Tk)

(33)

式中:i,k均为不同子系统个数;ψ(·)为示性函数,其定义为

(34)

其中,τ为区间[0.01,0.05]上的点,用来比较子系统间欧氏距离的差值,根据经验通常选定τ=0.02作为计算时的常量[27-28]。

Step7计算各子系统的故障风险评价分数为

(35)

Step8将计算得到的Hi按大小顺序进行排序,得分越高的其故障风险越高,得分越低的其故障风险越低,分析i个子系统的得分情况,并基于此对故障风险不同的子系统采取不同的状态监测与视情维修策略。

在维修优先级决策场景下,同时考虑故障风险与维修时间进行维修优先级排序能为现场维修工作提供多角度的指导。然而,故障风险评估结果中有负数的存在,不满足CODAS评估的数据条件。考虑故障风险评分指标中的欧式距离、出租车距离与平均维修时间均对维修优先级有着同方向的影响作用,即某子系统负向距离的数值越大,其故障风险越高,表示该子系统更容易发生故障、发生故障的紧急程度越高、故障的影响更严重,且采用两种度量指标更能消除单一指标可能带来的随机误差[28]。与此同时,平均维修时间越长,意味着维修周期越长、停车时间越长,更应该及时、提前维修,以保证列车的安全、正常、高效运行,故应该同时考虑欧式距离、出租车距离与平均维修时间,从故障风险与维修占用时长两个方面进行综合判断各子系统的维修优先级。

对于维修优先级决策,将Step5计算得到的欧式距离、出租车距离数值结合各子系统平均维修时间作为新的熵权法-CODAS决策矩阵,重复Step1～Step7,记求得的维修优先级评价分数为MAi,i=1,2,…,m将其按大小顺序排序,得分越高说明其在研究对象中是处于优先选择的地位即维修优先级越高,并以此作为指导现场维修的理论基础。

在基于熵权法-CODAS的故障风险评估过程中,采用重心法规范化矩阵,减少了不同量纲的指标对评估带来的影响;采用熵权法一定程度上消除了评价的主观性并为决策矩阵分配了权重;采用CODAS评估以欧氏距离为首要度量指标、出租车距离为次要度量指标,相比基于负向距离的评估、理想点法等其他多维决策模型,提高了评估的灵敏度[12]。利用欧式距离、出租车距离与平均维修时间构建维修优先级指标体系,从故障、维修两个角度出发,可为CBTC车载系统的各子系统的检修方式提供理论参考。

3 实例分析

选取北京地铁某线路CBTC车载系统从2018年7月22日至2020年11月13日的故障记录文本作为数据准备,文本主要包含有故障原因、故障发生时间、投入运营时间、故障间隔时间、故障紧急程度、各部件维修时间、维修方式、处理人员等信息,以经挖掘推理得到的可靠性影响度、逆平均利用率、故障发生度、故障发生紧急程度作为评价指标,按故障发生次数,将CBTC车载系统划分为ATP子系统、DCS子系统、MMI子系统及其余子系统(ATO系统、DSU系统等其余子系统)四类子系统,每个子系统都有若干部件组成。对CBTC车载系统下属子系统进行故障风险评估与维修优先级决策,不同类别的子系统故障发生次数与所占总故障次数比例如表2所示。

表2 子系统故障发生次数及所占比例

3.1 故障风险评估指标体系建立

求解故障间隔时间的频率分布情况,并利用核密度对概率密度进行初步估计,得到ATP子系统、DCS子系统、MMI子系统、其余子系统与CBTC车载系统的频率直方图与核密度估计见图4。

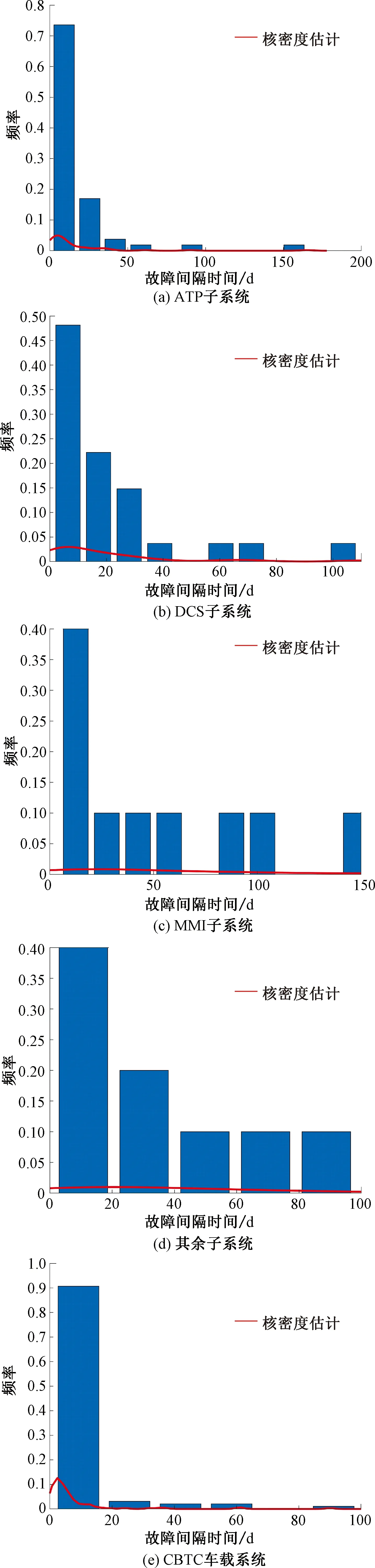
图4 ATP子系统、DCS子系统、MMI子系统、其余子系统与CBTC车载系统的频率直方图与核密度估计

由图4可知,CBTC车载系统及其子系统的故障间隔时间数据大致呈对数正态分布或威布尔分布。接下来,对这两种分布模型的有效性进行检验。

利用极大似然估计求得CBTC车载系统及其子系统故障间隔时间的对数正态分布与威布尔分布参数如表3所示。

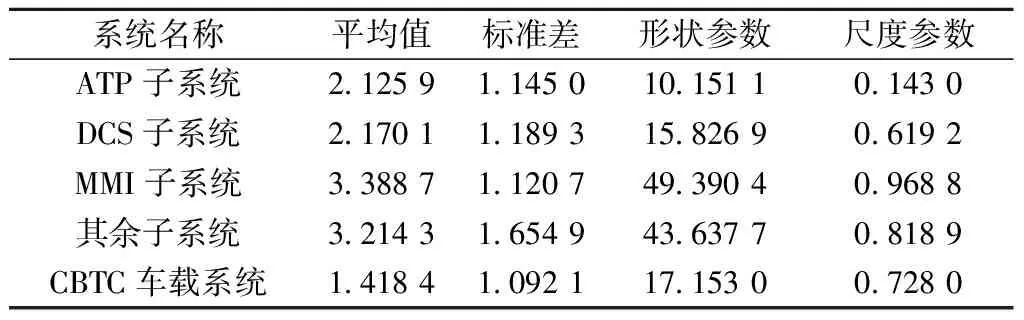
表3 故障间隔时间对数正态分布与威布尔分布参数

利用K-S检验法对对数正态分布与威布尔分布进行检验,检验结果如表4所示。

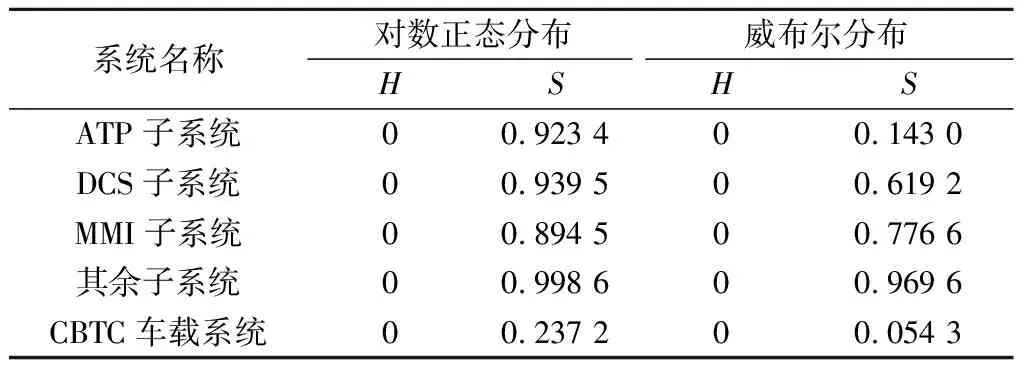
表4 对数正态分布与威布尔分布的检验结果

由表4可明显看出,CBTC车载系统及其子系统的故障间隔时间均满足对数正态分布与威布尔分布,且故障间隔时间服从对数正态分布的概率要显著大于服从威布尔分布的概率,因此,选定对数正态分布作为最优分布模型。将表3所求得的平均差与标准差代入式( 8 )中,得到不同系统的可靠度函数见图5。

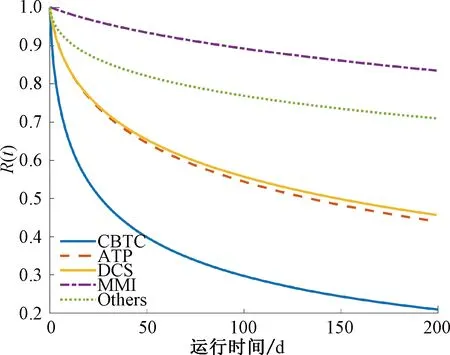
图5 CBTC车载系统及子系统的可靠度函数曲线

由图5可见,ATP子系统与CBTC车载系统的可靠度曲线距离最近、形状最相似。将每条曲线离散为201个数据点,分别求取各子系统可靠度曲线与系统可靠度曲线的弗雷歇距离作为衡量曲线相似度的指标,并将求得的结果代入式(13)、式(14),解出曲线相似度与可靠性影响度如表5所示。

表5 子系统可靠性影响度评价指标

各类子系统的系统平均无故障运行时间如表6所示。

表6 子系统平均无故障运行时间

将表6数据代入式(15)、式(16)中,求得各类子系统的逆平均利用率矩阵mur为

mur=[0.444 7 0.525 1 0.433 8 0.365 1]T

(36)

同时,将表2数据代入式(17)中,求得各类子系统的故障发生度矩阵λ为

λ=[0.061 5 0.036 7 0.011 8 0.011 8]T

(37)

同时,记录各子系统故障次数与每次故障的紧急程度如表7所示,并代入式(18)～式(21)中求得各子系统故障发生紧急程度矩阵EM为

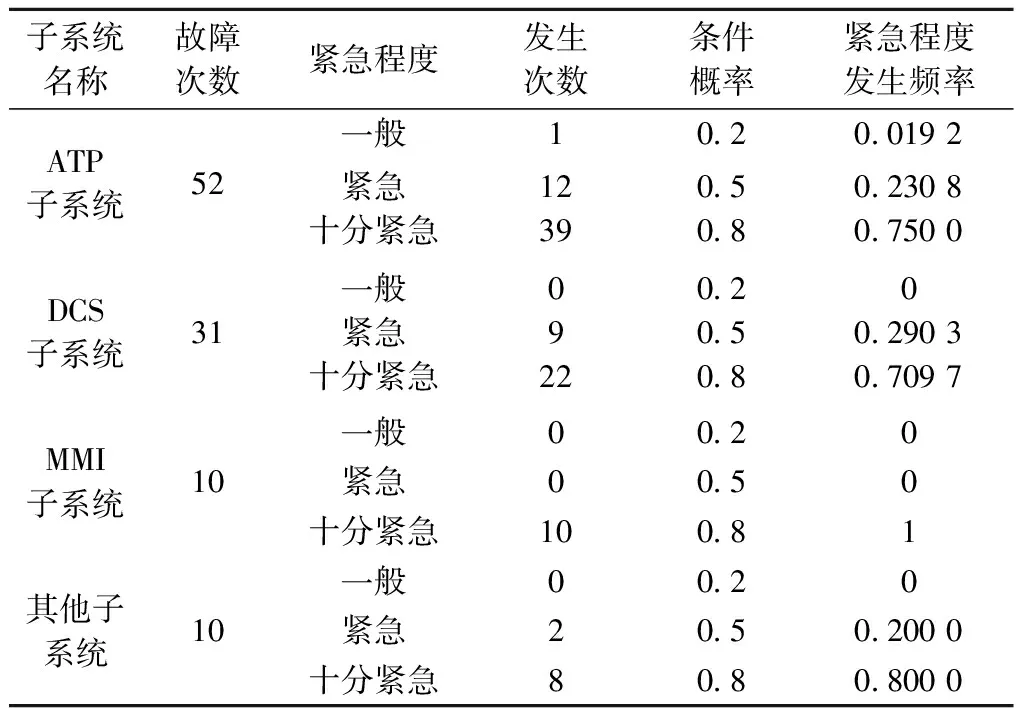
表7 各子系统故障发生次数及其紧急程度

EM=[0.355 0 0.214 6 0.077 7 0.071 8]T

(38)

各类子系统的故障风险评估指标见图6。

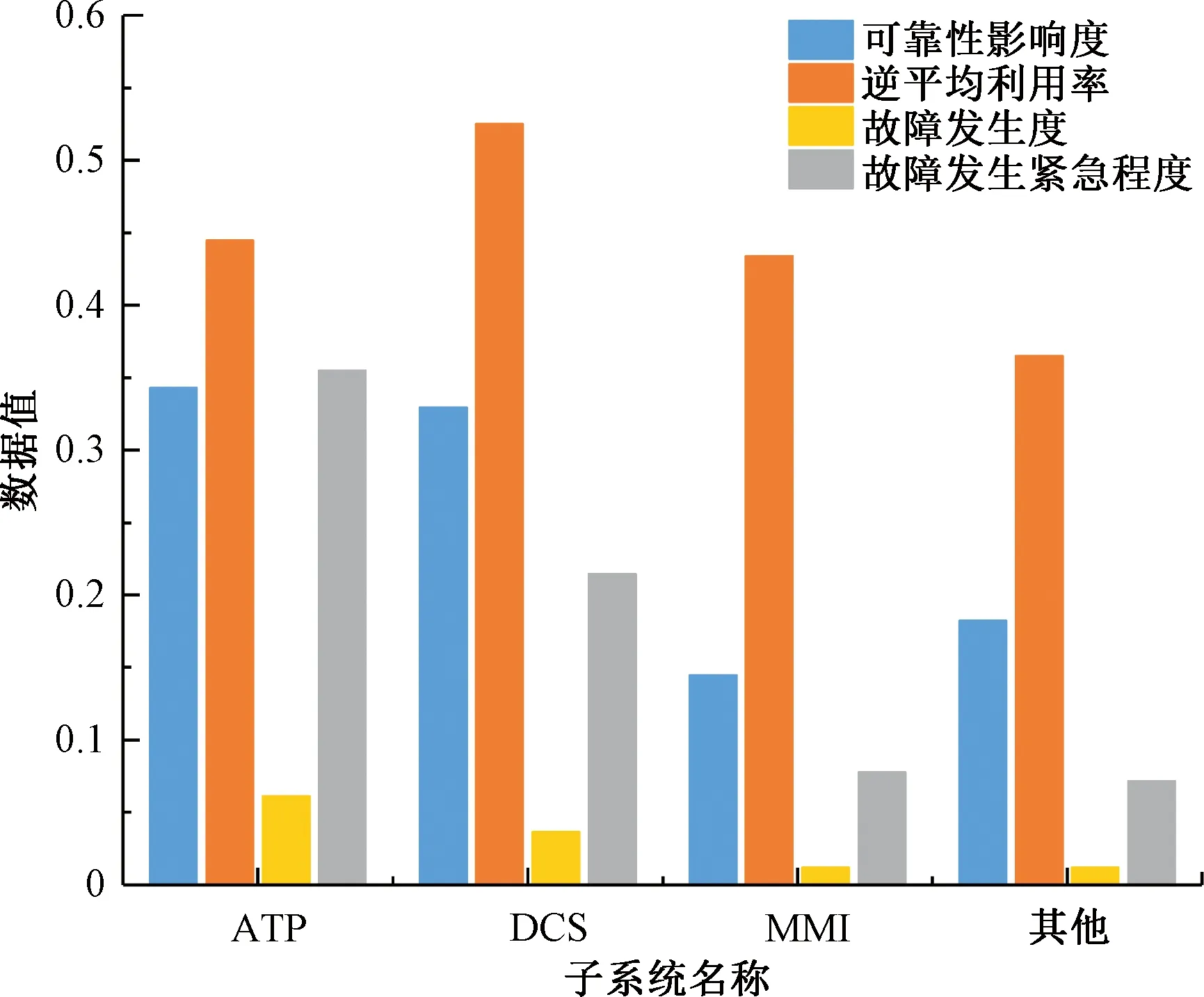
图6 各子系统的故障风险评估指标柱状图

因此,得到故障风险评估初始决策矩阵IV为

(39)

3.2 CBTC车载子系统故障风险评估

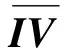
(40)

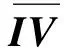
(41)

同时,由式(30)可得为

NP=[0.070 0 0.107 0 0.038 6 0.040 7]

(42)

若评估指标与负理想解距离越远,则故障风险越大[29]。

计算各子系统的在故障风险评估场景下的欧式距离与出租车距离如表8所示,由式(30)～式(31)可知,负向距离的数值大小与欧式距离相等。

表8 故障风险评估下欧式距离与出租车距离

将求得的欧氏距离与出租车距离代入式(33)、式(34)中,求解各子系统间的CODAS评估值如表9所示。

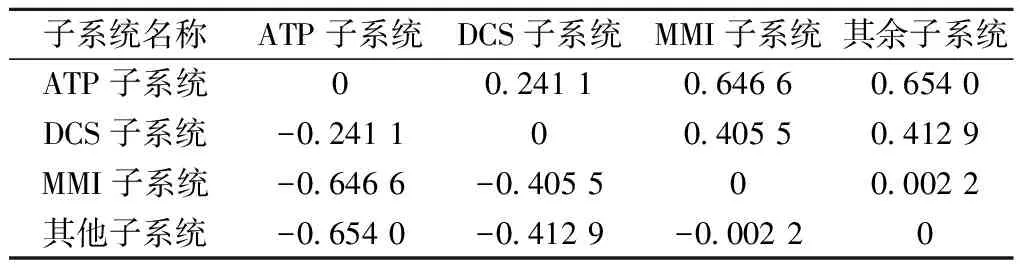
表9 各子系统间CODAS评估值

将表9结果代入式(35)中,求得CBTC车载系统各类子系统的故障风险评估结果如表10所示,同时以负向距离作为检验模型有效性的标准。

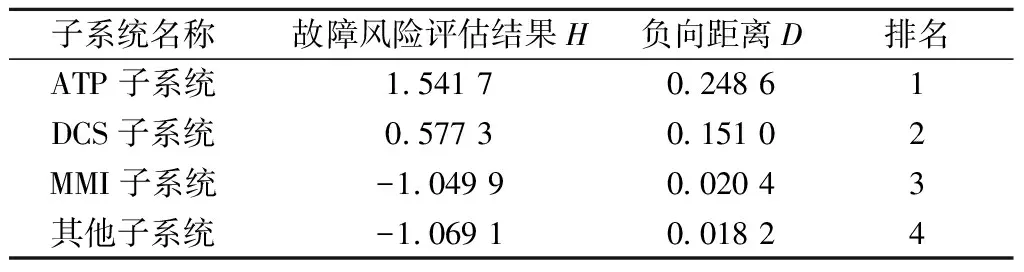
表10 各子系统故障风险评估结果

由表10可以得出,HATP>HDCS>HMMI>HOthers(以Others代表其他子系统),DNPATP>DNPDCS>DNPMMI>DNPOthers,得分越高表示故障风险越大,即本文所提出的基于CODAS的故障风险评估方法是可行的。与此同时,基于CODAS的不同评估结果间的绝对值、方差等统计量的数值要显著大于基于负向距离求得的评估结果间的统计量的值,对于某些场景下负向距离相近或相等的情况下能够为决策人员提供更为显著的风险评估结果,更有利于辅助决策人员快速筛查各子系统的风险等级。对于本文所选取的CBTC车载系统各子系统,ATP子系统在约束条件下的故障风险评估中表现最差,其他子系统表现最好,在现实生活中,按照此排序对各类子系统采取不同的监测手段与维修方式、重点关注故障风险评估结果较大的子系统的可靠程度及运行工况,对于保证城市轨道交通的安全高效运行具有良好的预防效果。

3.3 CBTC车载系统子系统维修优先级决策

CBTC车载系统子系统的平均维修时间与基于平均维修时间及维修优先级排名如表11所示。

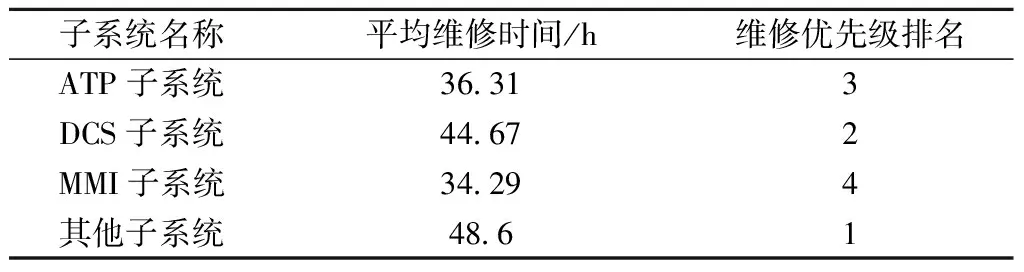
表11 各子系统平均维修时间及维修优先级排名

由于故障风险评估值与故障平均维修时间具有同尺度变化趋势,即其值越大表示维修优先级越高。由于故障风险评估值存在符号不相同的问题,会影响矩阵标准化的结果,故将表8中的欧式距离、出租车距离与表11中各子系统故障平均维修时间作为维修优先级层CODAS的决策矩阵IV′为

(43)

采用重心规范化的方式减弱评价指标不同量纲对评估结果的影响,得到规范化矩阵为

(44)

采用熵权法求得权重矩阵w′={0.318 4 0.307 4

(45)

同时由式(44)可得负理想解点为

NP′=[0.019 8 0.010 5 0.155 0]

(46)

计算各子系统的欧式距离与出租车距离如表12所示。

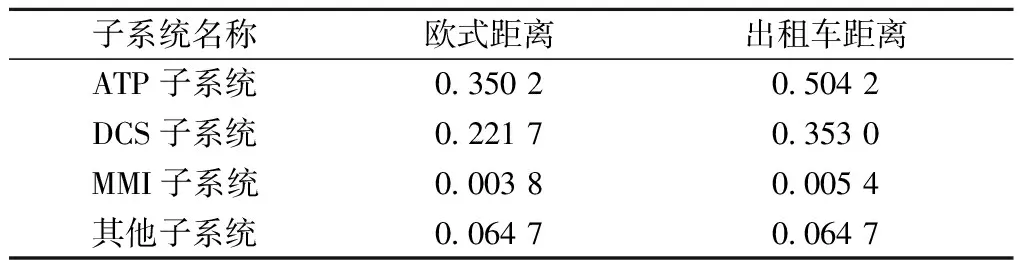
表12 维修优先级决策下欧式距离与出租车距离

将求得的欧氏距离与出租车距离代入式(33)～式(34)中,求解各子系统间的CODAS评价值如表13所示。

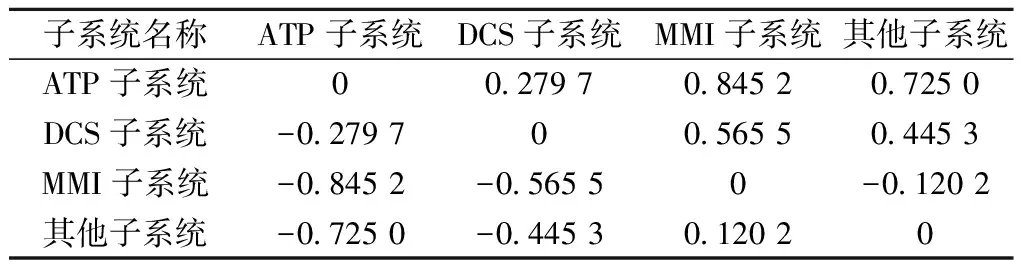
表13 各子系统间CODAS评估值

将表13结果代入式(35)中,求得CBTC车载系统各子系统的维修优先级评估结果如表14所示。

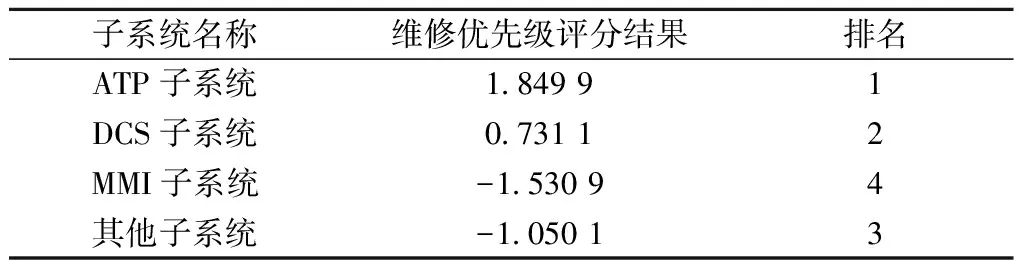
表14 各子系统维修优先级决策结果

如表11与表14可得,若只考虑平均维修时间的影响,则MAOthers>MADCS>MAATP>MAMMI,在考虑负向距离与平均维修时间的共同影响下,MAATP>MADCS>MAOthers>MAMMI。二者维修优先级决策评估结果有所差异,在本文所提方法中,ATP子系统在维修优先级评估下得分最高、表现最为突出,是当前评估模式下的最优先选择对象,即综合考虑决策条件,ATP子系统的维修优先级处于最高水平。在现实维修工作时,应考虑具体的约束条件对不同的子系统进行维修,通常情况下,尽可能地以智能运维的角度出发全方位考虑维修顺序,是高效、低费用率维修的坚实基础。基于CODAS的CBTC车载系统子系统故障风险评估与维修优先级决策评分总体折线图见图7,其中,得分越高表示该类子系统在当前评价指标中表现越差,即故障风险越高、维修顺序越靠前。本文所提出的维修优先决策方法,综合考虑了故障风险约束与停机时长约束,能够为实际的维修决策提供理论依据,保证列车的安全运行。

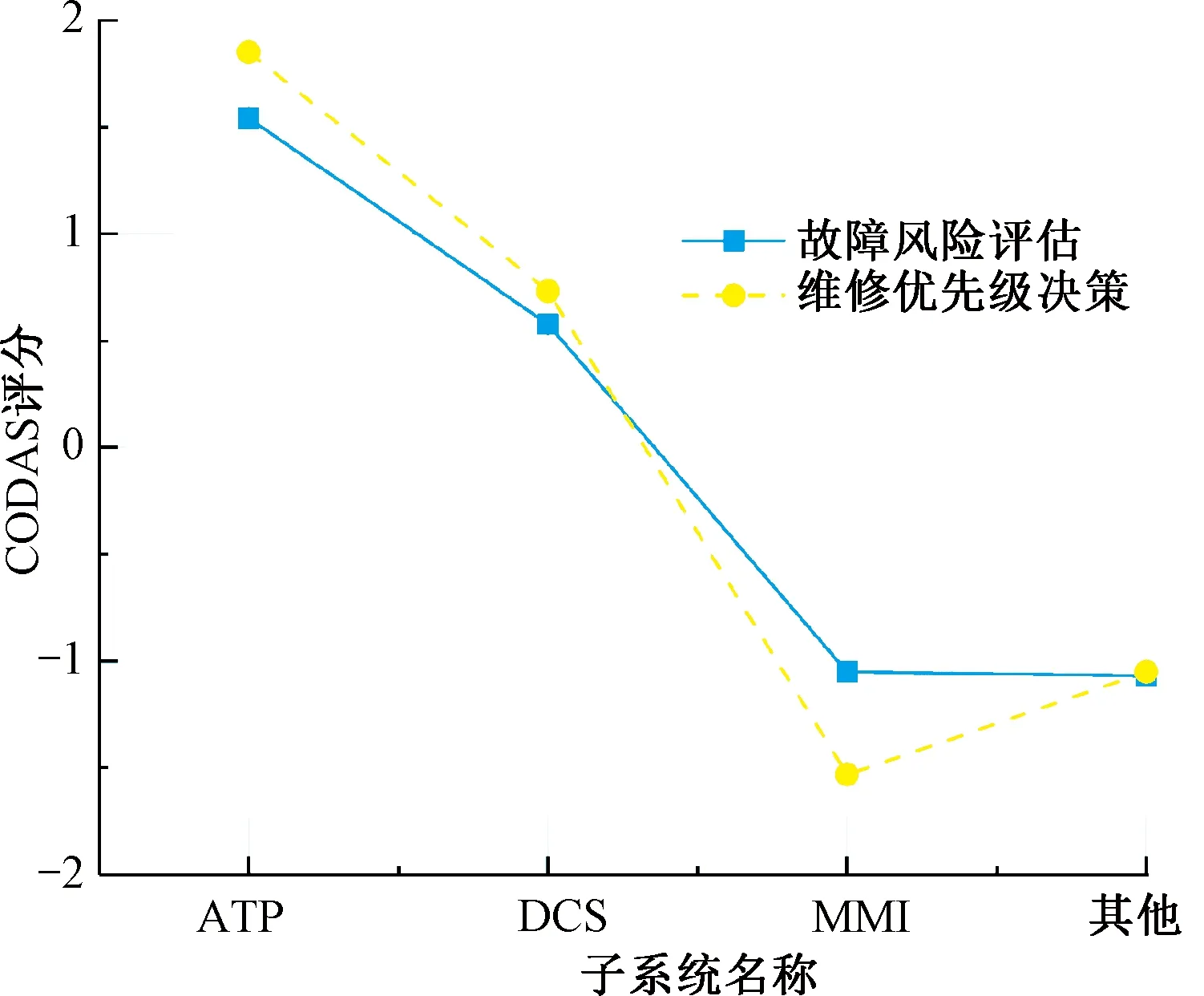
图7 各子系统的故障风险评估与维修优先级决策的CODAS评分值

4 结论

(1)提出了基于故障间隔时间的可靠性影响度指标的构建方法,通过极大似然估计与K-S检验选择对数正态分布为最优分布模型,并拟合故障间隔时间在时间尺度上的演化趋势,求解CBTC车载系统及其子系统的可靠度函数曲线,利用弗雷歇距离计算子系统可靠度曲线与系统可靠度曲线间的曲线相似度,并依此求解可靠性影响度的具体数值。

(2)以可靠性影响度、逆平均利用率、故障发生度、故障发生紧急程度为基础,构建故障风险评估指标体系;以故障风险评估中获取的CBTC车载系统子系统的欧式距离与出租车距离,结合平均维修时间,实现了对维修优先级评价指标体系的建立。

(3)提出了一种基于熵权法-CODAS的CBTC车载系统子系统故障风险评估与维修优先级决策方法,相比传统的基于负向距离的多维决策评估方法,基于熵权法-CODAS的评估方法得到的评估结果的数学统计量的值要更清晰、显著;同时,所提出的方法能够为CBTC车载系统的安全管理提供新思路、对于指导CBTC车载系统的可靠性维护具有积极的现实意义。