漫谈数域中的一致性

江苏省无锡市新洲小学 余晓华

《义务教育数学课程标准（2022年版）》指出：数学课程内容的一大特点就是整体性。如何更好地体现新课标理念的整体性，就是在数的概念的学习和接受过程中，从数形成和发展的角度出发，沟通知识之间的实质性联系，由浅入深，层层递进，螺旋上升，建立起框架式的结构性知识链，从源头上让学生感受到整体性的存在。

一、凸显通码——计数单位，感悟数的概念的一致性

在小学阶段，学生主要学习自然数、整数、小数和分数，这些数的产生与发展都源于人们的生活实践。

（一）寻找不同数的同频点，同声相应

在最初数系学习中，学生是从自然数开始认识数的。一年级上学期学生在实际情境中感悟并理解数的意义。从图1中可以看出，单一情境中，有1个滑梯、2个秋千、3个木马……在抽象到小圆点时，通过相应的方法，让学生感受到圆点表示与之相等的数量，再过渡到数字表达。还可以给学生创设相关情境：比1多1的是2，比2多1的是3……抽象成一致性的元素单位后，前后之间的关联性就更明显了，可明显看出数与数之间的联系是如此紧密。计数单位依次累积，一个衍生一个……在十进制的助推下，自然数就这样产生了，在累积过程中，永远遵循着同类计数单位的累积，同一个数领域的同类叠加，在一个个往后数的过程中，学生初步体会到了数是对数量的抽象，同时也理解了数的意义，无形中感受到了计数单位的一致性，从而很好地发展了数感这一核心素养。

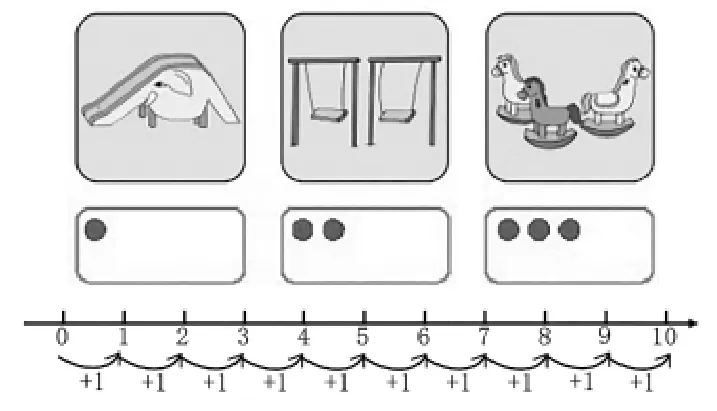
图1

在学习数的认识内容后，学生接下来接触到的是三年级上学期的分数，当把一个蛋糕平均分成两份，没法用自然数表示结果的时候，分数就顺其自然地出现了。学生在感受意义的过程中，也捕捉到了最基本的分数单位：每份大小一样，两个就是1，两个相同的分数单位可以进行累积。分数单位其实也就是分数这个领域中的计数单位，感悟到了这一点，才能更好地感悟分数的本质。分数的累积与自然数的累积，在本质上是完全一致的。数家族的规则是如此统一，且都是同类生长。

学生认识的第三种不同类型的数是三年级下学期的小数，小数是与众不同的，但是又与分数有着千丝万缕的关系。当把“1”平均分成10份，每份是，写成小数就是0.1；把“1”平均分成100份，每份是，写成小数就是0.01……在这个平均分的过程中，我们看到了小数产生的全过程，小数就是分数的另一种表达形式，同时发现了小数最根本的元素——计数单位：0.1、0.01、0.001……而且0.1、0.1+0.1=0.2、0.2+0.1=0.3……依次往后数，数的过程就是计数单位在逐步累积的过程，而且是相同计数单位的叠加，产生了不同的小数，小数的衍生与自然数和分数有着彼此相通的感觉。

（二）探测不同数的共振带，同生共长

在整数、小数和分数的产生中，还有着奇妙的同向性，那就是当计数单位依次累积时数就变大，当计数单位依次递减时数就相应变小，这个同向性与数的概念的一致性也有着紧密的联系。虽然不同数位上的数字所对应的计数单位不同，但是都有着这样的同向性，在这样统一原则的情况下，数家族稳固而持续地同生共长。

（三）经历不同数的数学化，同条共贯

认识数的关键是理解数的建构过程，在数的产生过程中，我们看到了整数、分数、小数这三种不同类型的数集之间的一致性，这种一致性是由基本元素即计数单位所联结的。数的发展过程就是计数单位的发展过程，每个数位上的计数单位均不同，但是相互之间却有着紧密的联系，而且有着相同的规则——满十进一。因此，计数单位占据数的认识中的核心地位，这也是整数、分数和小数的共通之处，数的意义、数的大小、数的表达等都是基于此才有了意义。学生在认识计数单位的过程中，感悟到了数的概念本质上的一致性，从而整体把握数的概念的本质，发展了持续的数感，更学会了用数学的思维思考问题。

建立数之间的联系，就要以计数单位为核心要素来统领数的概念。感悟数的概念的本质，带领学生经历由数量到数、由整数到分数再到小数的形成过程。这个过程是知识的发生、发展过程，也是数学化的过程。学生经历了这个过程，才能够体会知识的本源性与一致性。

二、通码衍生——运算规则，理解加减法运算的一致性

在整数、分数和小数的学习中，学生有了整体认识和关联性思考，打破了知识间的壁垒，这对学习运算是有帮助的，很多问题都会迎刃而解。因此，用联系的眼光、整体的方向、全方位的视角学习知识，不仅能够加深理解，更能达到有效的正迁移，使学生基于数的概念的一致性进而顺理成章地理解数的运算一致性的合理性。

加、减、乘、除本质上是一体的，所有的运算都可以还原成加法，加法是所有运算的基础；就算法角度而言，所有运算的根本就是计数单位与计数单位的运算。其中起到润滑剂作用的还是数的概念中的通码——计数单位。

在整数的加减法运算中，计算原则是相同计数单位相加减，如：

216+135

=2（百）+1（十）+6（一）+1（百）+3（十）+5（一） （数的组成）

=（2+1）（百）+（1+3）（十）+（6+5）（一）（加法交换律、加法结合律）

=3（百）+4（十）+11（一）

=3（百）+5（十）+1（一）（满十进一）

=351

数的概念是基于计数单位把数组装起来，数的运算是基于计数单位把数拆解开来，再进行同类累积，从而得出结果。

在小数的加减法中，计算原则同样是相同计数单位相加减，如在上面的两个数字中间任意位置点上小数点，求两数的和：

2.16+1.35

=2（一）+1（0.1）+6（0.01）+1（一）+3（0.1）+5（0.01）（数的组成）

=（2+1）（一）+（1+3）（0.1）+（6+5）（0.01）（加法交换律、加法结合律）

=3（一）+4（0.1）+11（0.01）

=3（一）+5（0.1）+1（0.01）（满十进一）

=3.51

虽然上下两题的数字组成一样，但是因为小数点的出现，打乱了原来数的平衡，让数字所在数位上的数值发生了变化，所以得出的结果就不一样了，但是它们的本质是相通的。在第一步写数的组成中，将数打回原形，寻找到这个数的缘起，即它是怎么来的。在数的组成中，我们明显看到了数的组成的分类，几个百、几个十、几个一……不同数位上的数字表示不同的数值，分类的思想已明显呈现，通过加法交换律和加法结合律，让同类的“入一家”，也就是遵循着相同计数单位“入同一家”的原则，然后才能相加，在加的过程中，同生共长的感觉已然显现。

不光整数加法和小数加法遵循着这样的原则，整数减法和小数减法也遵循着同样的原则。分数加减法也同样都遵循相同计数单位相加减的原则，分数中的计数单位就是分数单位，分母相同，表示单位相同，分数在加减的过程中，也是几个几分之一加减几个几分之一，等同于整数、小数中的几个百加减几个百，几个十加减几个十……与整数、小数运算保持了一致。这也就意味着单位个体一样的同类，才能在均等条件前提下进行加减，与整数、小数加减法的计算法则是一致的。

在教学中，学生学习知识的过程是循序渐进的。在这个过程中，教师要揭开数及其运算表面的层层面纱，让学生的知识串联成链，环环相扣，螺旋上升，自由生长……那么，学生结构性的知识将成为他以后学习的一个生长点。所以学习完小数加减法后，教师可以让学生主动梳理小数加减法与整数加减法的异同，在梳理中逐渐建立关联，沟通数的运算的一致性。同时，在学习完分数加减法后，教师可以引导学生思考分数加减法与之前的整数加减法、小数加减法是如何嫁接起来的。整体设计教学，在数的认识、数的运算的每一节课中贯彻上述思想，那么在所有数的概念与运算的学习结束时，就能进行融会贯通的复习，实现算理贯通、算法统整。只有形成结构性的知识，才能更加深化学生对这个知识点的认知。

三、单位创生——稳固共识，培养惯性思维

在数学学习这个漫长的过程中，学生由对数的概念的一致性沟通过渡到对数的运算的一致性的理解，而这种一致性对学生的后续产生的不仅仅是点状的物理作用，也可以产生有效的“化学反应”，从而使学生对数学中的一致性产生更为稳固的认识。

在“元、角、分”“米、分米、厘米”……这些涉及单位的所有类型的描述中，在进行加减运算时，同样要遵循相同单位才能相加减的原则，这个原则也是从学生一开始认识这些单位时就形成的固有的认识，元+元、角+角、分+分。在这个过程中，也体现着相同单位相加减，与数的运算的一致性是同向而驰的。同时这个原则解释了五年级上学期小数加减法运算要将小数点对齐的原因，对学生理解知识起到了画龙点睛的作用。如4.75元+3.4元，为什么将小数点对齐再计算结果才是正确的？因为4.75元就是4元7角5分，3.4元就是3元4角，元和元是同类的，角和角是同类的，分和分是同类的，这样相加才是符合规则的。在这个过程中，也渗透着相同单位相加减的原则，让这个一致性产生了良好的辐射作用，学生的思维得到了拓展。其实，所有相关单位都遵循着这样的一致性，单位量不断累积继而产生更大的数，只是在同类单位中遵循的进率有所不同，所有的同类生长都是一致的，这种一致性也是数学体系中所有元素生长的根。

为了达成上述目标，教师要重视对教学内容的整体分析，明白“数”与“运算”的一致性；抓住统领性概念，深化对数学知识本质的理解，提炼能建立数学知识间的结构与联系、发挥核心作用的数学概念；揭开笼罩在数及其运算表面的层层面纱，由此建构数学单元学习主题统整下的脉络清晰、条理分明、相互联系的数学知识体系；设计合理的教学案例，带领学生经历知识的发生、发展过程，建立知识之间的联系，体会知识的本源性、一致性与整体性；引导学生体会不同数学知识之间数学学习方法的可迁移性，学会用发展的眼光看问题，形成科学的思维习惯，从而有效地发展学生的数学核心素养。