地铁仿真环境下的非暴露空间鲁棒定位方法研究

汪琮棠，薛志刚

（全图通位置网络有限公司，北京 100176）

0 引言

非暴露空间是相对于暴露空间定义的，多指室内或半室内场景，如地铁、隧道、煤矿、地下车库等。在暴露空间中，北斗卫星导航系统作为提供时间和空间信息的全球系统，在灾害监测、货物跟踪、人员定位、坐标测量等领域有着重要应用［1］。然而，由于其天然脆弱性（信号弱、穿透能力差、易受干扰等），在非暴露空间导航与位置服务中存在壁垒。针对空间结构复杂、电磁信号传播非平稳、资源分布易变化、定位精度要求高、位置服务高并发等难题，泛在、精准、连续、智能的非暴露空间导航与位置服务成为亟待拓展的领域。

当前，地铁非暴露空间场景定位技术快速发展，相关产品高速迭代，可应用于地铁时空的典型定位技术包括蓝牙、射频、Wi-Fi、RFID、超宽带（Ultra Wide Band，UWB）等多种技术。在既有文献中，肖雄等［2］描述了一种基于蓝牙技术的地铁站台定位系统，该系统通过蓝牙定位结合专用定位基站及标签，为车站工作人员提供定位导航服务；陈晓玉等［3］考虑了Wi-Fi传输距离远、部署简单等特点，在地下停车场的车辆实时定位系统中采用基于位置指纹的Wi-Fi室内定位方法，帮助用户准确判断停车位置；陈龙鹏［4］针对现有RFID 定位精度不高的问题，提出一种基于双神经网络的RFID 室内定位算法，解决了因环境变化而路径损耗系数仍取固定值所造成的定位误差，实现对室内运动物体较高精度的跟踪定位；张志忠［5］利用超声波定位技术具有的信号易处理、成本低、定位精度高等优势，优化了基站超声波探头布置效率低、超声波收发端同步计时不准确、超声波速率易受温度影响等问题，改善室内定位效果。

综上所述，针对地铁非暴露空间环境的定位问题已形成相对完善的研究体系。基于安全性、成本预算和定位精度等多方面考量，选取UWB 定位技术进行亚米级高精度定位。不同于传统通信方式，UWB 定位技术采用ns～μs 级的极窄脉冲成形，具有功率谱密度低（≤110 dBm）、工作频段高（7 235～8 750 MHz）、电磁兼容性和抗干扰能力强、穿透性能好、电量消耗低、发送功率小等特点，是广泛应用于智慧交通、智慧工地、智慧矿区等千行百业工业级和消费级的成熟定位服务技术。室内定位技术的定位精度取决于覆盖场景遮挡情况，以及多径性、定位节点密度、信号强度、信号码片速率、待测量参考信号长度等多种因素，主要定位技术的应用效果对比见表1。

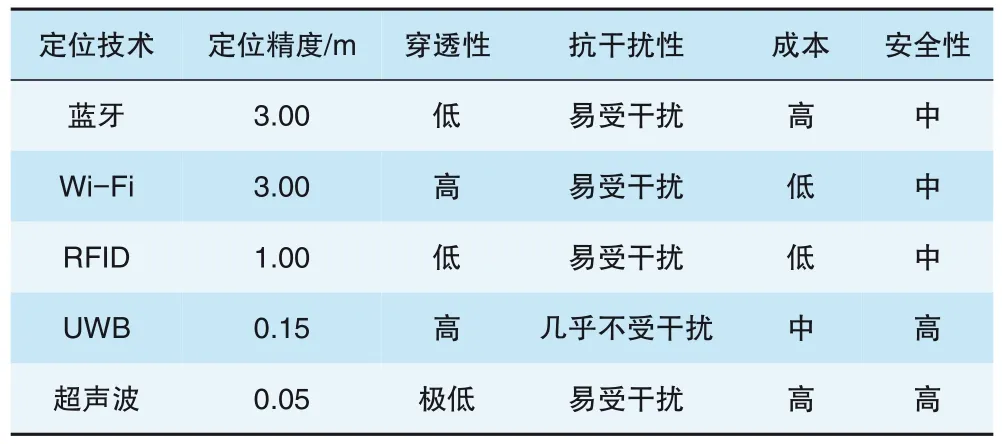
表1 定位技术应用效果对比

基于UWB 技术的无线定位系统一般由定位标签、定位基站和解算软件构成。通过在特定区域布置合理数量的定位基站，不间断地采集人员、车辆、资产、工具上的定位标签回传的时空坐标数据，实现室内空间实时精确定位、监控、预警等功能。然而，室内生产环境布局和拓扑易受人为因素影响，定位基站往往不能实现理想化布置。基站根据可获得的安装站点的实际情况进行布置，可能高低不平；由于室内遮挡物较多，基站大多被布置于有一定高度的天花板或墙上，而被定位目标通常在地面移动，存在显著的高度差。由高度差导致不理想的基站几何构型，影响二维、三维位置信息解算，造成空间内定位精度变差。

针对以上问题，提出一种地铁仿真环境下的非暴露空间定位方法，研究实际复杂场景中的UWB 定位改进算法，提升复杂基站构型下的UWB 定位性能。考虑同时对基站和标签进行时间同步的复杂性，选取到达时间差算法（Time Difference of Arrival，TDOA）进行定位精度优化，获得实时运动轨迹。TDOA定位算法仅保持基站之间时间同步即可，计算过程中不需要进行信号解调，可直接处理接收到的信号。在充分收集、统计并利用定位基站和环境的先验信息后，利用贝叶斯估计转化为鲁棒的TDOA定位算法，并采用遗传粒子群混合算法实时解算迭代待测目标的位置估计值，保障非暴露空间UWB立体布站的灵活性和鲁棒定位性能。

1 UWB定位技术

UWB 无线电是从信号带宽角度定义的无线电信号［6］，冲激信号是其最典型的实现方式，以占空比极低、带宽极窄的脉冲（脉冲宽度一般在ns或ns级以下）作为信息载体进行数据传输。UWB 无线通信技术直接通过发送和接收极窄脉冲进行数据传输，而传统的窄带通信方式需借助载波进行信息传输［7］。

1.1 UWB信号特征

根据美国联邦通信委员会（FCC）规定，UWB 设备带宽被定义为：-10 dB 相对带宽>0.2 或占用带宽>500 MHz，UWB 设备与传统窄带通信系统的功率谱占用带宽对比见图1。其中，fc为中心频率；fH-fL为上截止频率与下截止频率之差；相对带宽为截止频率之差与中心频率之比。UWB 信号的频谱显示信号幅度下降至原始峰值的1/10（即-10 dB）时，该信号的相对带宽>0.2，优于传统窄带信号，使UWB 信号能在更宽的频率范围传输数据或信息，提供更高的数据传输速率和容量。

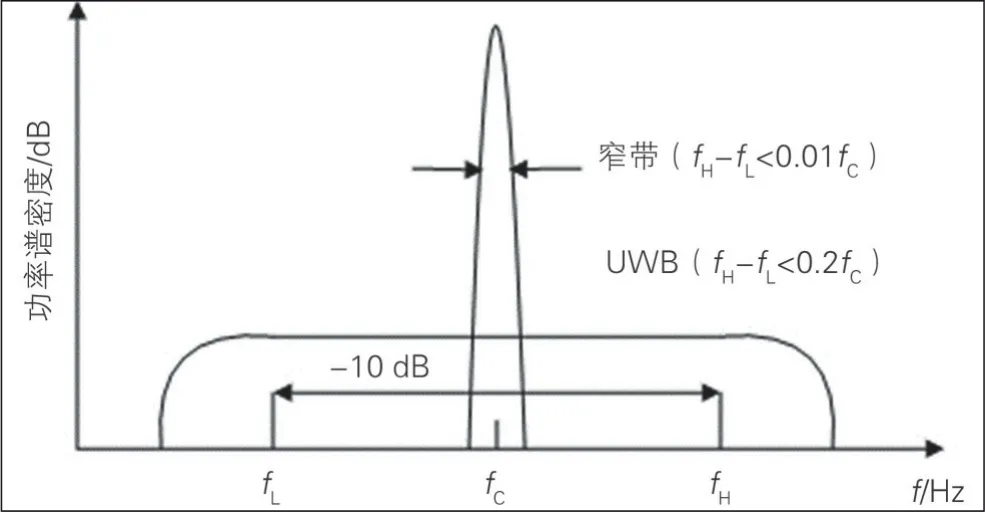
图1 UWB与窄带的功率谱占用带宽对比

2023年1月4日，中华人民共和国工业和信息化部无线电管理局发布了《超宽带（UWB）设备无线电管理规定（征求意见稿）》，将我国UWB 使用频段调整为7 235～8 750 MHz，并对设备发射功率限值进行了统一（≤-41 dBm/MHz）。

UWB 系统通常可以采用多种不同的波形，且这些波形都是单周期脉冲波形，如高斯脉冲波形、升余弦脉冲波形等［8］。由于高斯脉冲信号频谱宽度较宽，且其各次微分具有较简单的形式，方便分析研究，因此，UWB 系统中最常用高斯脉冲或其微分形式作为信号波形（见图2）。在实际应用中，随着高斯脉冲求导次数增加，其时域峰值数量也增加，反而加大了接收机捕获信号的难度。因此，工程中常用高斯脉冲的二阶导数作为UWB系统发射的脉冲信号：

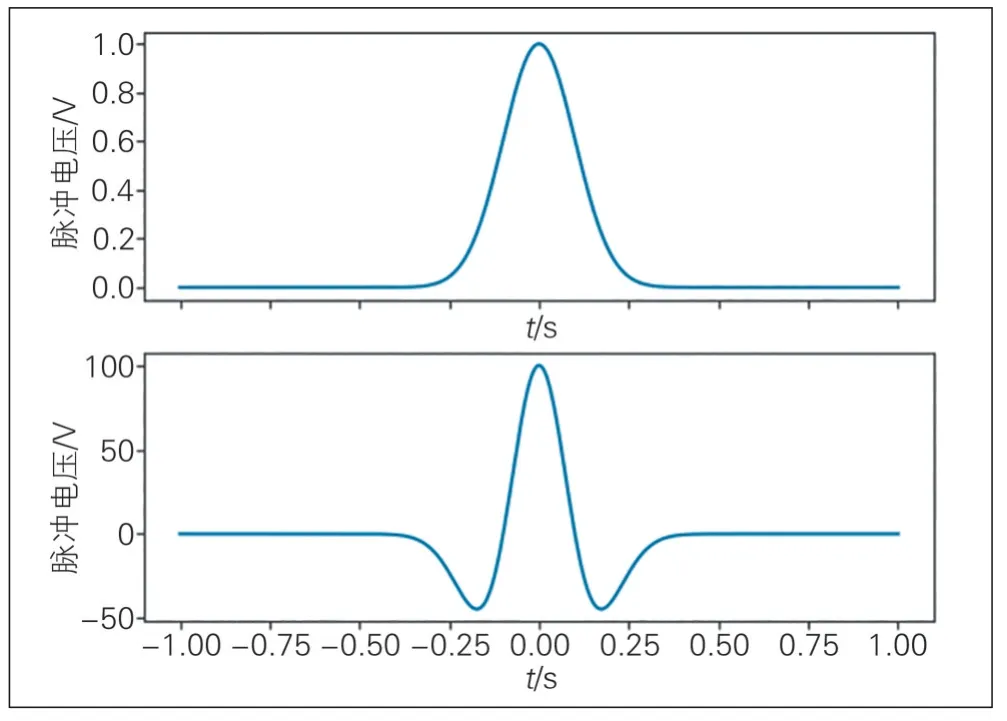
图2 UWB信号波形

1.2 UWB信道特性

根据不同的应用范围和频率范围，信道模型可分为：低频信道模型、IEEE 802.15.3a 高频信道模型、IEEE 802.15.4a 高频信道模型。其中，低频信道为1 GHz 以下，高频信道则针对FCC 标定频段3.1～10.6 GHz。IEEE 802.15.4a 模型在原有IEEE 802.15.4 标准基础上，增加了对UWB 技术的支持，允许信号在非常宽的频带上传输，从而使信号具有很高的分辨率和准确性。模型中主要有路径损耗、小尺度衰落、多路径时延扩展等参数［9］。

UWB 信道的大尺度衰落主要由在无线网络传播中的路径损耗所导致，损耗值可以近似于自由空间中的衰落。当信号从发送端到达接收端时，会经过许多障碍物，对信号产生衰减和反射，导致信号到达接收端时功率减少。高频信号的波长更短，更容易被建筑物、树木等障碍物所吸收，长距离传输造成路径损耗增加。因此，对于UWB 定位系统，其占用频带带宽很大，路径损耗不仅与距离有关，也与频率有关，表达式如下：

式中：PL为路径损耗；d0为基准距离，可由测量决定；PL（d0）为在基准距离和基准频率（fc=5 GHz）条件下的衰减值；d为信号从基站到标签的距离；γ为路径损耗指数；Xσ服从正态随机分布，其标准偏差为σ。

UWB 的小尺度衰落主要由多径效应引起。无线电信号在传播过程中，受自然环境等因素影响，产生多个不同的到达接收机的路径，不同路径到达的无线电射线相位不一致且具有时变性。同一接收设备从不同传播路径收到的信号衰落程度各不相同，对使用互相关技术获取时延参数估计的方法产生较大影响。不同路径的信号相互干扰、相互叠加，接收器接收的信号发生一系列如信号强度、相位、时延等方面变化，导致信号小尺度衰落。由于UWB 脉冲极窄、波长极短，一般不考虑其相位变化带来的影响，因此其随机相位的快速变化不会引起瑞利衰落，表达式如下：

式中：m为Nakagami分布的因子；Ω为幅度平均值。

在多重衰落叠加影响下，认为UWB 脉冲发射并经过多径环境后，信号成簇到达接收机，并表现出衰减的特征。若关注每簇最高的路径，将接收机观测所得信道冲激响应简化如下：

式中：N为多径条目总数；an为该径的增益；τn为多径的时延。

UWB 信道的模型是由上述模型综合之后得到的，这些模型中的参数值都是IEEE 802.15.4a 工作小组根据大量实测数据拟合得出的。然而，由于各种应用场景的复杂多样性，不同的工作环境下拟合得到UWB 信道模型参数差别很大，还需要进一步进行位置估计。

1.3 UWB定位算法

1.3.1 TDOA算法原理

TDOA 算法是一种基于多个接收器间的时间差测量，从而实现对信号源的定位的算法。首先，选定1个基站作为参考，当定位标签发出信号时，信号在到达每个基站之前会经历一定的时间延迟。通过比较每个基站记录的时间戳，将每个到达时间值相减，计算出信号在每个基站的到达时间差。多条双曲线的交点可得待测标签的位置坐标（见图3）。如果只求得待测标签的二维空间坐标，则至少需要3个基站参与定位，建立2个双曲线方程即可求解。

图3 TDOA定位原理

设共有N个基站参与计算，第i个基站的位置坐标如下：

基站和目标位置的关系方程如下：

建立（x，y）和距离差之间的关系方程组如下：

式中：ri为第i个基站到目标位置之间的距离；ri，1为基站BS1 到目标位置的距离与第i个基站（除第1 台基站外）到目标位置的距离之差。通过最优化算法求解，可得待测标签的位置估计值。

TDOA 算法可以在低信噪比下实现高精度定位，通过测量接收器间的时间差，抵消信号所受干扰。相对于其他定位算法，TDOA具有高精度、高可靠性、抗多径效应强等优势。另外，TDOA算法仅要求基站间时间同步，不要求基站与标签时间同步，由于基站位置固定，基站之间进行时间同步相对于基站和标签之间进行同步更容易实现。该项目的TDOA 算法采用IEEE 1588V2协议中PTP协议所提供的高精度时间同步功能，设计了单区域多基站串联相结合的系统网络架构和时间同步系统，实现了整个网络的时间同步精度优于1 ms，相邻基站间的时间同步精度优于1 μs。

定位算法评价指标常采用均方根误差，不仅考虑定位误差的大小，还考虑误差的方向和分布情况，能真实反映定位算法的真实定位精度，表达式如下：

在高斯噪声环境下，小区半径设为1 000 m，随着参与定位的基站数增加，能利用的TDOA测量值的数目增加，可得更高的定位精度（见图4）。但是，当参与定位的基站数≥5，定位精度改变不大。因此，利用TDOA测量值的定位算法，需要参与定位的基站至少为3个；当参与定位的基站数≥5，定位性能达到最优。

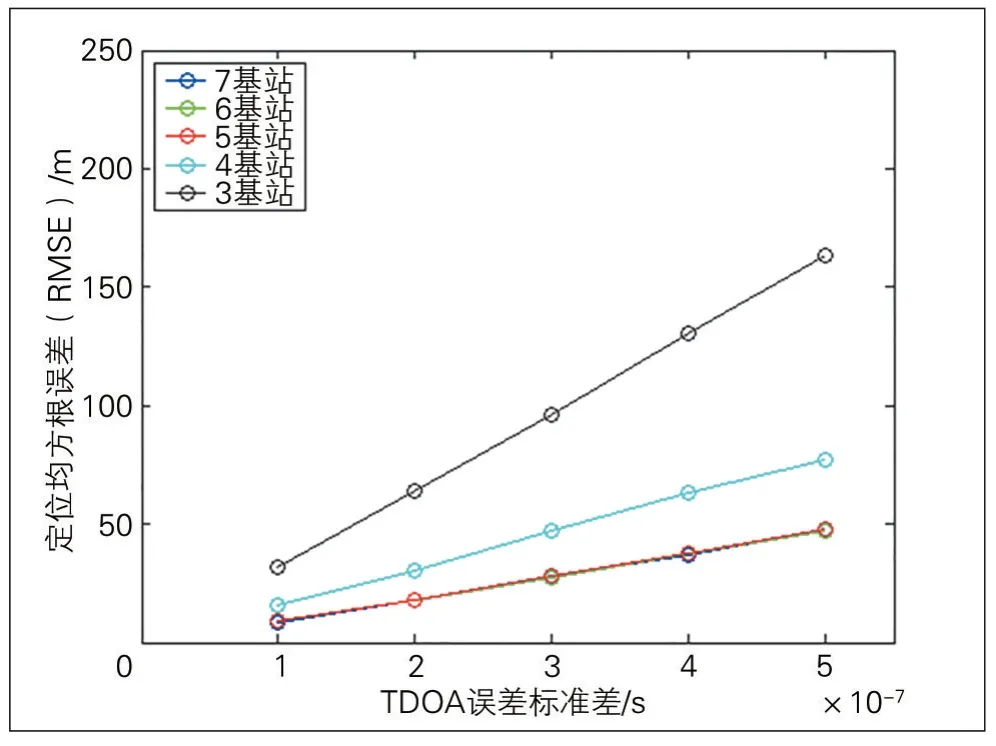
图4 不同基站数目下TDOA算法性能对比

1.3.2 基于最大后验估计的TDOA定位算法

目前，针对TDOA定位中求解非线性方程的计算复杂度高、时间长等问题已有诸多研究，如Chan 算法、Fang 算法、泰勒级数展开法等，但这些方法对初始解要求较高，涉及繁杂的矩阵运算，且易陷入局部最优解。胡骏等［10］以TDOA/AOA混合定位算法为对象，用最大似然法得到定位标签的估计函数，将估计函数作为适应度函数产生初始种群，用IMPSO 算法对种群进行寻优，得到最优估计位置。而在非暴露空间定位场景中，被定位目标的位置或运动特征通常有一定的先验知识，该类先验信息可很大程度上弥补由基站布置约束所导致的问题。观察待定位目标所处定位环境，其统计学特征可看作是目标在三维空间中的先验信息，表达式如下：

式中：A为n行3列矩阵；θ为3维列向量；b为n维列向量；n∈（1，2，3）；Σ为n维联合正态分布的协方差矩阵。θ代表待测目标三维空间的坐标估计值，当n取不同值时，分别对应以下3种约束：

（1）当n=1 时，目标以一定概率分布在1 个平面附近；A为平面的法向量；Σ为目标距平面距离分布的方差。

（2）当n=2 时，目标被2 个平面所约束，目标以一定概率分布在1 条直线附近；A中包含2 个相交平面的法向量；Σ为目标距直线距离分布的方差。

（3）当n=3 时，目标被3 个平面所约束，目标以一定概率分布在1 个点附近；A中包含3 个相交平面的法向量；Σ为目标距离该点分布的方差。

基站观测得基站间到达时间差值的观测量为τdi，0，考虑测量噪声影响，表达式如下：

则N个基站的时差观测量构成向量：

根据贝叶斯公式，最大后验估计是使得后验概率函数p(θ|τd0)最大的θ，该三维空间坐标估计值的最大后验概率为：

观测量τd0的条件概率密度函数为：

θ的先验概率为：

式中：Υ(.)为广义无先验信息概率密度函数，其值为1；A⊥为与A中所有行向量正交的向量构成的矩阵，且自身行向量间也正交。代入后将最大后验估计等价于：

由此得到需要最小化的目标函数，将其作为遗传粒子群混合算法的目标函数以求解最优解。

2 遗传粒子群混合算法

传统迭代算法若要保证递归运算收敛，应选取恰当的初始值，然而面对算法计算复杂程度较高的场景，若初始值位置出现过大误差，则会导致定位结果发散，迭代不收敛的现象，定位效果远不及预期。遗传粒子群混合算法考虑了非暴露空间复杂场景的非线性和不确定性，在算法前期利用遗传算法生成一部分粒子群算法求解所需的初始位置值，优化了粒子群算法初始值的生成过程，在保证全局收敛的同时，随机分布于解空间中；算法后期采用粒子群算法进行快速局部搜索，通过强并行能力从多点出发寻找最优解，提高了求解最优解的效率，最后趋近于真实坐标值。

2.1 遗传算法

遗传算法（Genetic Algorithm，GA）是一种常用来解决复杂非线性问题的参数优化算法，在实际问题中，只需要给出目标函数的信息和一定的搜索空间（参数上下限），即可进行参数寻优。而且，它对初始值要求不是很高，也不受搜索空间内是否可微的限制。遗传算法根据达尔文自然淘汰假说，借鉴进化论中的优胜劣汰和适者生存的自然法则，模拟并深化自然环境中的基因遗传模式，形成计算模型。种群由经过基因编码的一定数目的个体或染色体组成，可以把每个个体都当成算法空间里的1个解。对每个种群中的独立个体进行编码，从而建立起表现型与基因型的对应关系模型。基因的变异和重组使大部分个体有了全新的表达方式、全新且多样的性状，让遗传算子具备选择、交叉和变异的功能。通过逐代筛选产生优秀的新个体也可作为目标的候选解进行迭代，可限制一些性能约束指标寻优来生成一部分粒子群算法求解所需的初始位置值。

若想解决一个用遗传算法优化的问题，需要先进行初始化种群。种群数量（N）要足够大，应尽量分散于解空间内；其次，要设置迭代次数（T），迭代次数应根据变量参数的多少决定，对于多变量的复杂优化，则需要迭代次数多一些，过少或过多的迭代次数都会对算法本身效率产生影响。遗传算法的核心则在于选择操作、交叉操作和变异操作［11］：

（1）选择操作。执行选择操作的过程是整个算法的第1步，基于个体适应度函数的选择不仅关系到遗传算法能否收敛，更是遗传算法用来选育优良子代的唯一基础依据，它通过预设的目标函数来对整个种群内的所有个体的染色体进行筛选，体现了全局搜索的特点。当对所有个体进行适应性函数值计算后，就进行判决择优，被判定为优秀通过的个体进入繁衍流程，开始交叉和变异操作。

（2）交叉操作。其实质是根据交叉概率（Pc）进行个体选取，种群中的每个个体之间要进行信息交互，随着交叉概率变大，信息交互增多。

（3）变异操作。变异概率（Pm）防止其最终变成局部最优解，通过改变个体染色体的值，如二进制编码中把0 值改为1 值以增加多样性，通常设为较低值。最后进行迭代次数比较，若满足迭代次数，则输出保存的最优的1代个体的值。

2.2 粒子群算法

粒子群优化算法（Particle Swarm Optimization，PSO）是一种源于对鸟群捕食行为研究的智能算法。该算法起源于小型群落生物寻找食物的过程。每个个体各自的飞行轨迹、飞行方向、速度等都是类似的，其内部传递着关于想要搜索的某个目标的信息。每个粒子的初始位置都不一样，有的近、有的远，但均按照一定准则（即适应度值）去搜寻目标。粒子在搜索的过程中，不断交流自身的位置信息，离目标越近，则越把自身位置通报给其他粒子，在已有信息和种群信息的帮助下，得到自己离目标的距离差。该过程中，为避免有的粒子脱离限定范围，要提前告知所有粒子的速度保持在某个范围以内。粒子群算法中的每个粒子被赋予2 个属性：速度和位置。速度代表移动的快慢，保证它们不会过远或过近；位置代表将选择的移动方向，是所有粒子争取靠近的目标值。

若考虑用粒子群算法解决问题，首先应设定PSO算法的各参数，如群体规模N、粒子速度界限vmax、位置搜索边界xmax、学习因子c1和c2、最大迭代次数T、惯性因子ω等。设D为所考虑的搜索空间的维数，在T次迭代中速度向量、位置向量分别为：

速度更新公式如下：

位置更新公式如下：

式中：pbestT为个体极值；gbestT为全局极值；r1、r2为0～1 区间内的随机数；种群规模N同上述遗传算法一样，衡量了算法精度问题，该值越大，种群之间相互沟通的信息协作能力越强；学习因子c1和c2为自我学习能力和向群体中优秀个体学习的能力，通过将最佳位置与自身位置作差，可感知自己提升多少、自己离群落中最好的个体差距多少。

粒子群算法在不满足最大迭代数终止条件时，应根据适应度函数计算所有个体位置的适应度值。适应度值作为评估种群中哪个个体将作为中心来吸引其他粒子聚拢，然后根据适应度值更新自己最好的位置，并根据种群以往最好的位置估算更新全局历史位置，不断朝向最优解靠拢。直至满足迭代次数条件后，跳出循环，结束粒子群目标函数优化过程。

2.3 遗传粒子群混合算法

遗传粒子群算法的改进是将前半部分用遗传算法全局搜索得到初始预优化种群，使优化种群随机分布于解空间，提高原有种群个体的多样性，获得粗定位值。遗传算法因为前期的选择、交叉、变异等操作可能会舍弃一些适应度值较高的个体，导致收敛速度慢等问题，所以后期需要一种更快速的局部收敛算法，即粒子群算法。在不断迭代的过程中，粒子群算法反复比较对迭代指定标准的设定，保留了较多的历史速度和位置较优解，并向着最优解不断靠拢，收敛速度较快。将粗定位值导入粒子群算法，形成新粒子群的初始位置，构建初始的粒子群种群。通常该2种算法的编码方式均可采用二进制或实数编码，因此2种算法在编码结构上有实现统一的可能。遗传粒子群混合算法操作流程见图5。遗传算法和粒子群算法采用线性组合方式，时间复杂度为一次阶，相较而言算法效率高。经过改进的遗传粒子群混合定位算法对于目标点寻优并输出最优初始坐标的效率更高，相比单一遗传算法具有求解速度快、收敛性好等优势，且提高了在非视距下的定位精度。

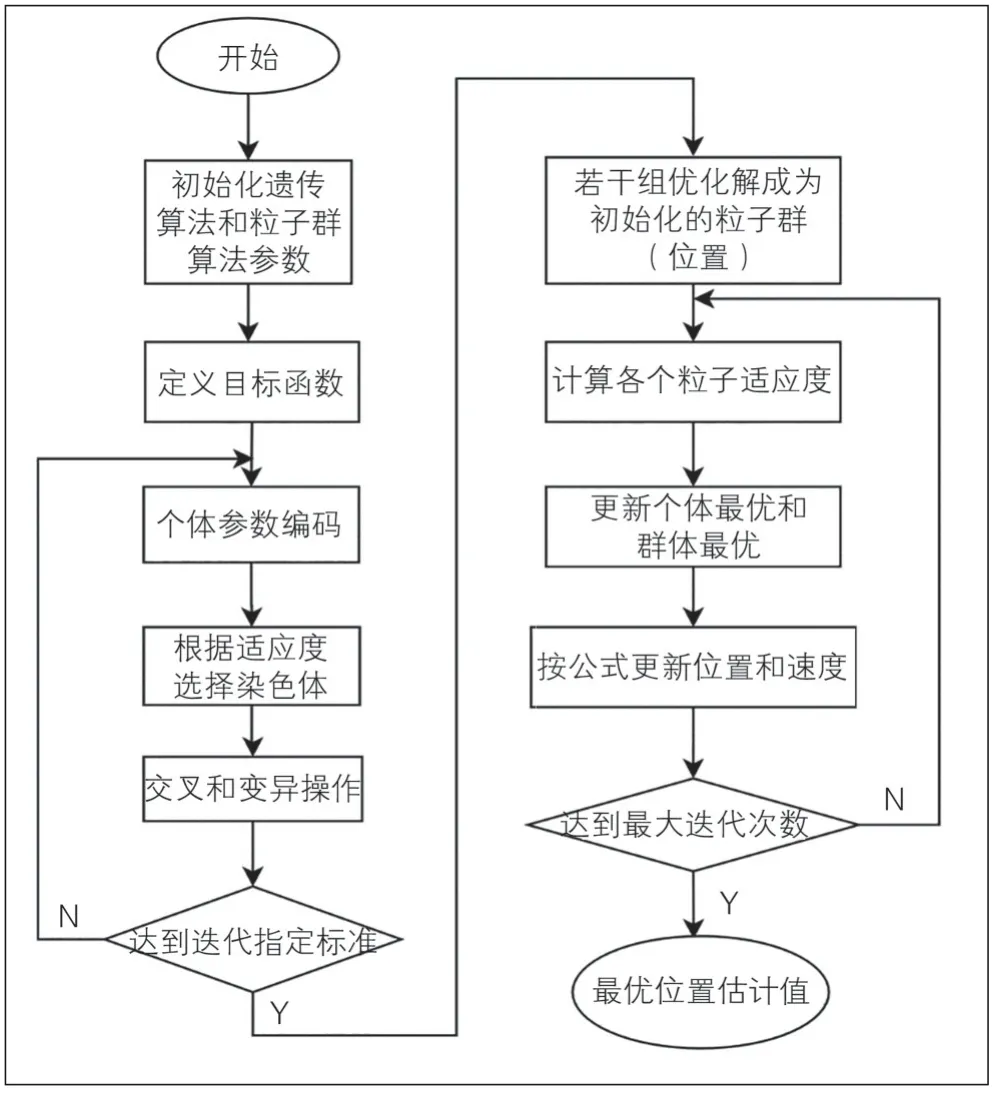
图5 遗传粒子群混合算法操作流程

为了验证提出算法的有效性，从常见测试函数中选用Ackley 标准测试函数进行仿真测试。Ackley 函数是一种不同维之间不可分离的多峰连续的测试函数。函数图像是1 个空间内由余弦波调制形成一个个孔或峰，从而使曲面震荡不平。对于输入的多维变量x，函数值y在x=(0，0，…，0)处有全局极小值0 点。这是一个复杂的函数，很多算法如梯度下降法都会在一定层次的迭代后陷入局部最优。运用该算法测试比较单一遗传算法和遗传粒子群混合算法的仿真结果，测试混合算法的收敛能力是否得到提高是对算法本身水平的考验。Ackley函数表达式如下：

式中：x的定义域标准是［-5，5］；学习因子c1=c2=2；种群大小设为100；迭代次数T设为50；交叉概率Pc=0.7；变异概率Pm=0.1。采用遗传粒子群混合算法，在最优函数值上更逼近零点、准确率更高。算法适应度收敛曲线对比见图6，可明显看出在收敛速度上，混合算法效率高于单个遗传算法。

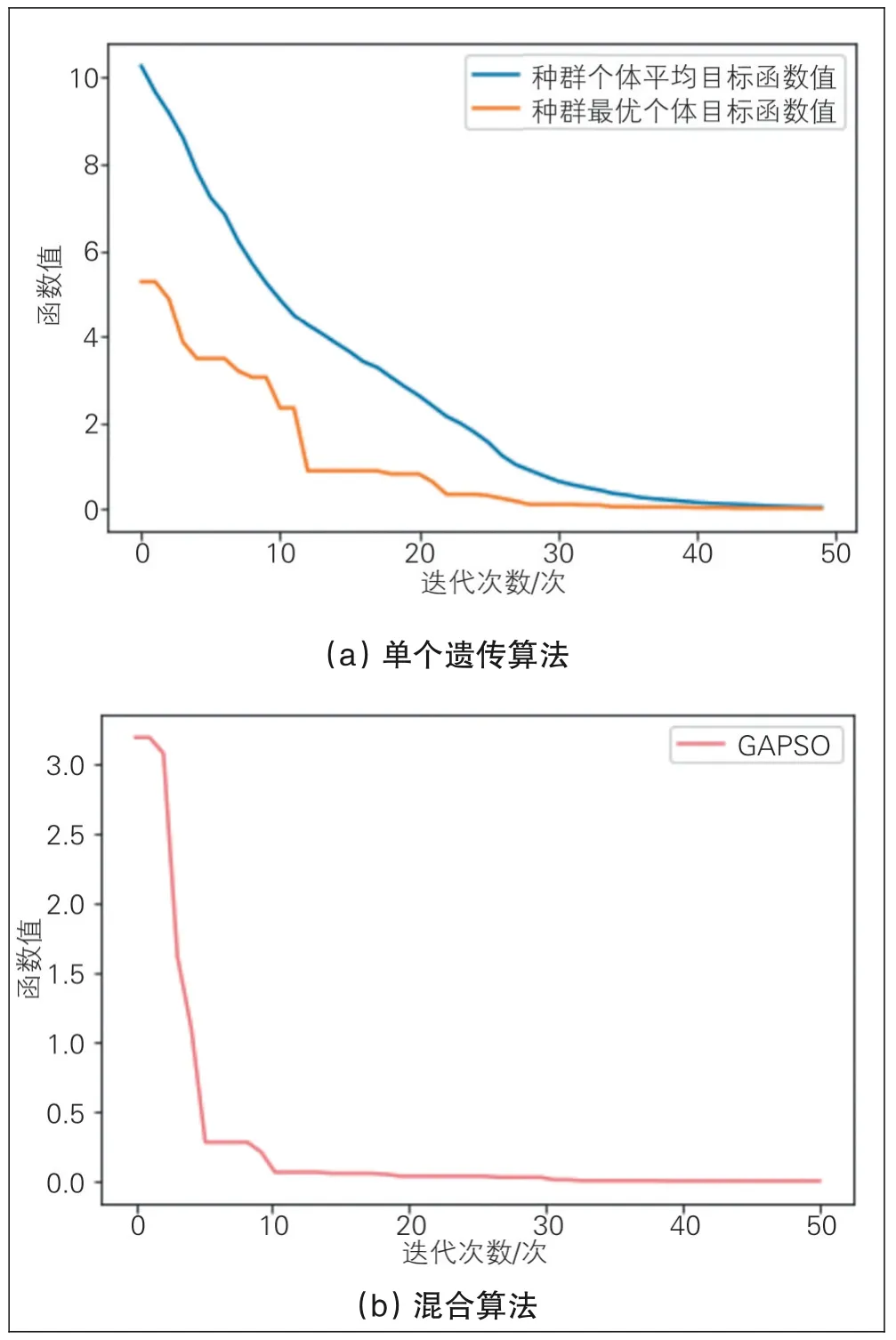
图6 算法适应度收敛曲线对比

3 鲁棒定位算法优化与性能验证

具有鲁棒性的系统和算法能够在输入数据发生变化时保持稳定性和可靠性，不会因为输入数据的变化而产生严重误差。经过前期研究，决定使用遗传粒子群混合算法，对基于最大后验估计的TDOA定位算法模型进行迭代寻求最优解，即待测目标位置信息，后续将用于地铁仿真环境服务器的可视化地图中，提升定位系统的鲁棒性能。

3.1 TDOA鲁棒定位算法优化

根据遗传粒子群混合算法操作流程（见图5），在初始化各项参数和目标函数之后，采用实数编码的方式对个体进行编码，保证在种群数量最大情况下得到最优结果。根据设定的交叉概率，随机将2个优良个体中的特定基因片段进行交换，重组得到具有新性状的优良个体；依据变异概率随机替换指定种群中的基因变异点，增加遗传算法中种群的多样性。在达到迭代次数后，生成若干组优化位置坐标，输入粒子群算法中。适应度值根据位置和速度公式进行迭代寻优，直至收敛趋近于0，此时认为当前得到的θ为最优位置估计坐标。重要步骤如下：

（1）定义适应度函数。

根据式（15），设：

将其作一阶泰勒展开变化，则：

式中：Jg(θ)为g(θ)在θ处的雅克比矩阵，代入可得：

在θ点用g(θ)的一阶泰勒展开近似原函数J后，转化为对于δ*的凸优化问题，原问题可转换为迭代求解偏差值δ，使目标函数具有最小值。

对于凸函数而言，任何局部极小值都是全局最小值，因此最小化目标函数可以得到全局最优解。遗传粒子群混合算法的适应度函数即为δ*，要求算法中的每个个体所对应的位置向量在目标函数中取得最小值。表达式如下：

（2）初始化遗传算法和粒子群算法参数。

首先，在仿真环境中布置多台基站，通过全站仪测量获得各台基站的三维坐标。标签会广播测距请求，获得基站与标签的双向测距产生的TDOA测量值。由基站坐标、TDOA测量值和平面约束方程共同生成初始的位置估计值θ0。其次，设置算法参数：种群数量N=100、迭代次数T1=T2=10、空间维度D=3、交叉概率Pc=0.7、变异概率Pm=0.1、学习因子c1=c2=1、惯性因子ω=0.5。参数选择将影响全局收敛速度和定位精度，根据先验经验选择以上参数。

3.2 UWB定位系统部署方案

UWB定位系统由定位标签、定位基站、服务器和授时同步设备等组件组成［12］。上述算法的解算单元集成于服务器，用于处理从基站和标签收集的数据，并计算待测标签的位置。服务器还具备添加基站和标签以及地图可视化的功能，实现对基站和标签基本信息的创建、修改、删除（基站：编码、型号、经纬高位置信息；标签：编码、型号、数据上传时间间隔），以及设置服务器IP及PORT，进行浏览查询。基站的主要作用是发送、接收信号，实现对定位目标的精确测量和定位。同时，基站之间可相互通信，实现对整个定位区域的覆盖和监测。UWB 基站采用基于NXP SR150 开发设计的UM150芯片，UM150芯片设计见图7。UM150集成了射频收发器、数字信号处理器、嵌入式处理器的UWB射频芯片，采用3天线设计，具有低功耗、高可靠性、高精度等特点，并支持多种不同通信协议和应用场景。

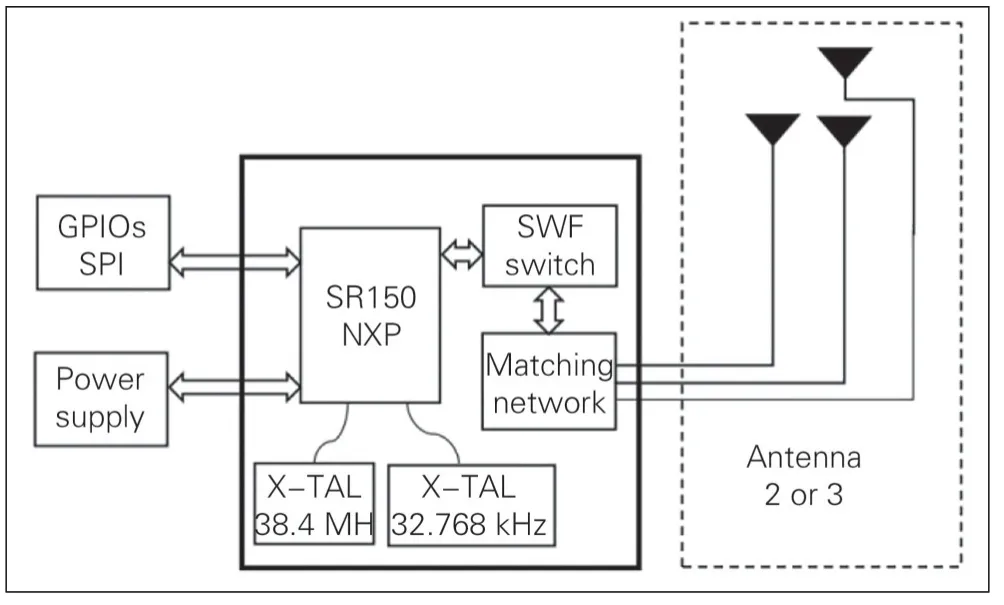
图7 UM150芯片设计

UWB定位系统通信过程见图8。如图8所示，标签向1组基站发出beacon 请求，基站将转发标签的beacon包传送至服务器，服务器收到消息按信号择优选取临近基站组，开始1次双向测距过程。当基站组接收到信息，发送Poll，接收标签的Poll back，然后向服务器上传TDOA 测距信息，如TDOA 测量值、坐标等。服务器组合多个异步测距信息，通过基于TDOA的鲁棒定位算法，计算定位信息取得最优位置估计值，并显示在可视化平台界面。

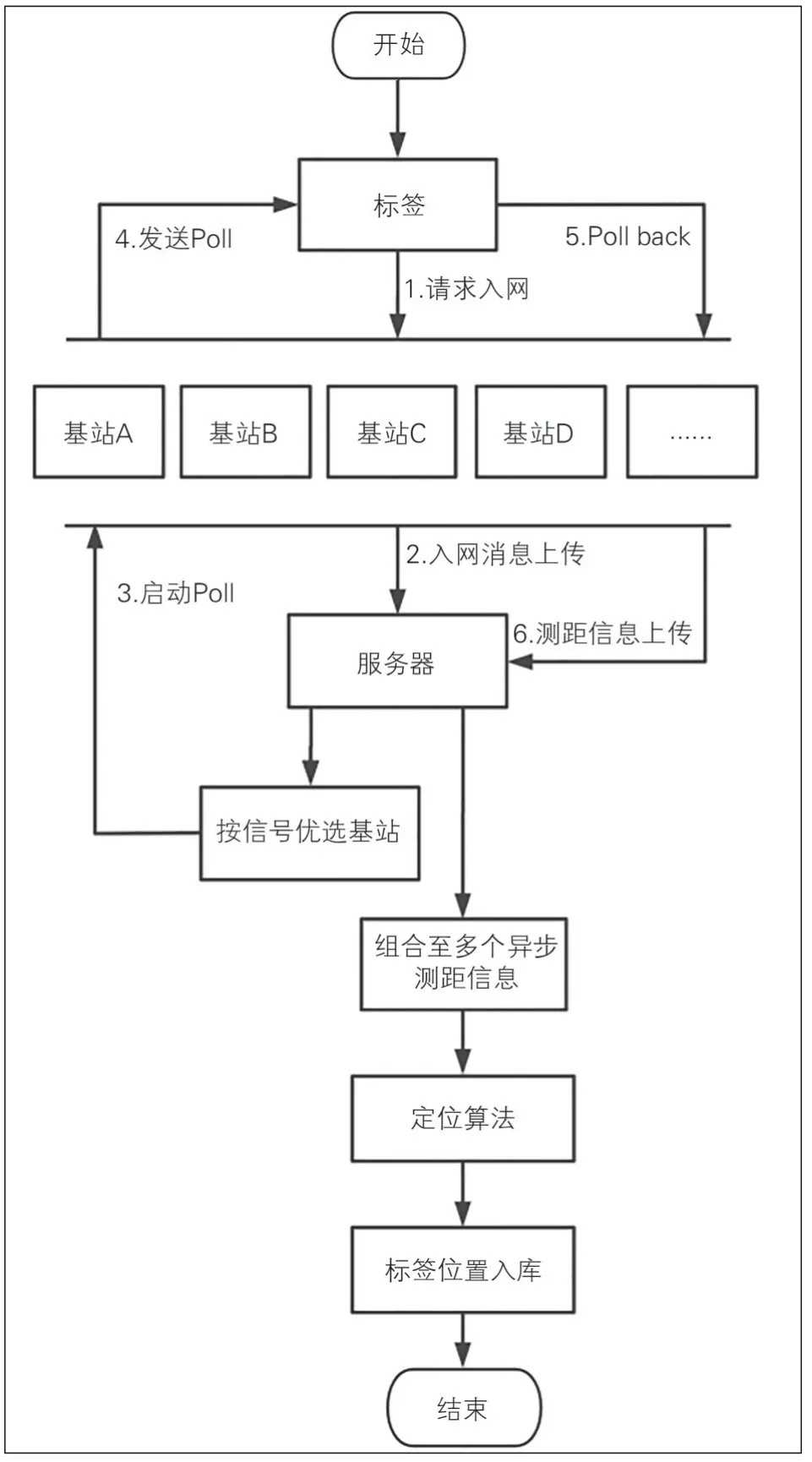
图8 UWB定位系统通信过程

UWB 基站覆盖范围可达40 m，考虑到模拟地下非暴露空间环境，选择在仓库布置6 台基站用于测试（见图9）。

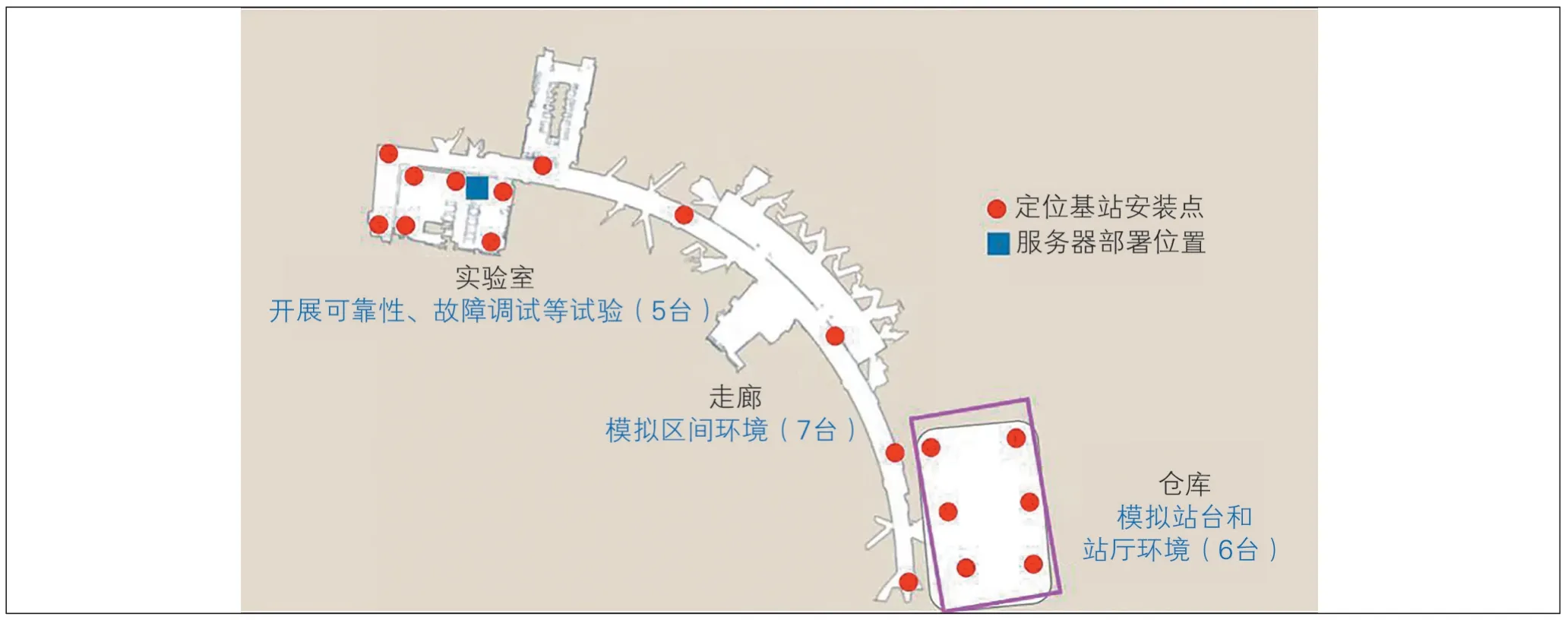
图9 UWB基站部署位置图

4 台基站位于屋顶，中间2 台基站位于靠近地面墙壁，以制造高度差。仓库长40 m、宽15 m、高3 m；模拟部分真实地铁站厅场景，部署高3.0 m、半径1.5 m的支撑柱；若干高约2.2 m 的柜子模拟展厅售货机；若干高约1.2 m 的杂物模拟闸机、售票机、防汛柜等设施。由于非暴露空间的环境局限性，部分基站不能安装于与地面平行的平面上，无法形成一个平面约束方程，所以特意构建仿真环境用于模拟。使用全站仪获得的各基站绝对坐标见表2。

表2 各基站绝对坐标

3.3 定位精度测试

北坐标和东坐标是经纬度地图投影后得到的直角坐标系下的坐标，即x轴和y轴；高程作为z轴。为研究地铁非暴露空间场景下的定位精度，至多只需要4台基站。考虑到各站地下各层均分布UWB 基站，仅对每层做二维定位即可。在仿真环境下，测试人员手持定位标签，在密闭仓库中沿S型曲线行走，其二维定位实时轨迹见图10。

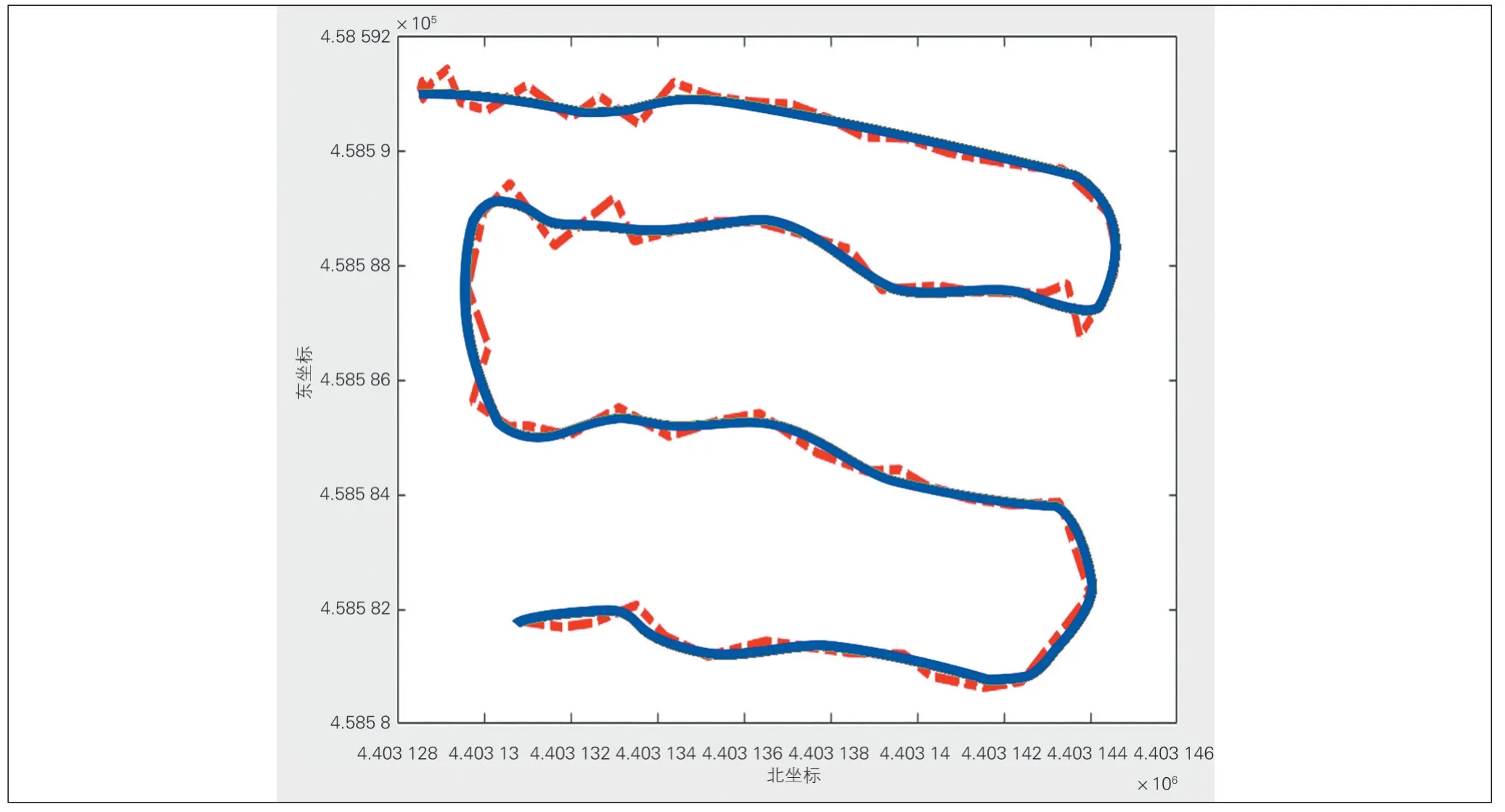
图10 二维定位实时动态轨迹

如图10 所示，蓝色实线为测试人员手持标签的行走轨迹，红色虚线为TDOA 动态定位轨迹。测试结果表明，通信基站与移动终端的测距信息实时刷新，可通过服务器实时接收并实时解算，即能够对处于杂物堆积的非暴露空间环境中移动终端作出与原点距离的测量。基于TDOA 的鲁棒定位方法可以很好地进行人员的动态定位并显示轨迹，在基站所围成的定位区域内误差保持在0.5 m 内，满足亚米级的精度需求。

在静态定位方面，测试人员手持标签位于仓库内某一位置不动，标签不停显示广播发送测距请求，择优选择基站进行定位解算，最终在可视化地图上呈现1个定点表示人员的位置。在地图上呈现的位置是固定的，但有细微的精度误差无法表达，需要调用真实测距信息。根据TDOA 测量值进行鲁棒方法优化后的定位误差见图11。如图11所示，其静态测量值相对稳定，4台基站的定位距离分别集中在5.42、9.27、5.12、4.73 m附近，误差均不超过0.2 m。静态测量值上下波动在可接受范围内，证明经过最大后验估计和遗传粒子群混合算法迭代后，位置估计值在非视距条件下保持较好的抗多径能力和鲁棒性能，不依赖基站位于1个平面的情况，满足实际场景厘米级高精度定位需求。

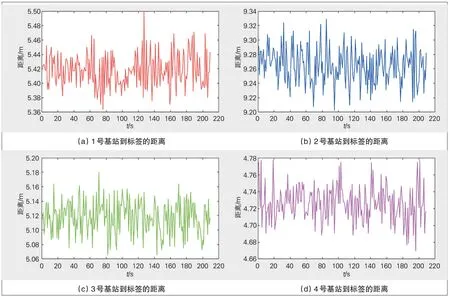
图11 基站定位误差统计

4 结束语

现代工业和社会化的快速发展带来大量复杂的非暴露空间环境，而基于位置服务的需求和应用也逐渐向非暴露空间转移。针对北斗卫星信号薄弱的非暴露空间区域，在地铁仿真环境中模拟站厅站台构建了完整的UWB 定位系统，包括基站、标签、服务器和授时设备，并探讨了UWB 信号在地下和室内环境中的定位方法。针对三维空间中定位算法受到基站几何构型的影响，研究提出基于最大后验估计的TDOA 定位算法，并采用遗传粒子群混合算法进行全局搜索和局部快速收敛。实验结果表明，优化后的算法在复杂几何构型下表现出鲁棒性，并能快速收敛，满足亚米级的高精度定位需求。