基于时间因子的蚁群算法在观光车路径规划中的应用
吴晓军 曾培耘 邓 林
(1.内江市特种设备检验所 内江 641000)
(2.四川省特种设备检验研究院 成都 610199)
对于坐标确定的初始点,求解在特定条件下的最优路径问题被称为旅行商问题(Travelling Salesman Problem, 简称TSP)。采用穷举法解决TSP 问题,其时间复杂度为O(n!)。例如:在初始点为11 个时,路径遍历的次数为362 880 次;初始点为50 个时,路径遍历的次数则快速增加到3.04×1064次。随着初始点的增加,穷举法在工程实践中由于耗时巨大已不具备实际意义。为解决实践中的TSP 问题,常采用一种称为蚁群算法(Ant Colony Optimization,简称ACO)的启发式算法。其原理如下:单只蚂蚁在行动过程中会在移动路径上留下一种化学“信息素”,在相同路径上经过的蚂蚁越多,信息素的浓度则越高。蚂蚁会倾向于向信息素浓度更高的路径移动,随着蚂蚁数量的增加,就使得短路径上的信息素浓度不断升高,长路径上的信息素浓度则增加缓慢甚至不再增加。同时,信息素浓度最高的路线成了最佳路线。通过使用计算机模拟蚁群行为,利用信息素的正反馈原理,能更好地求解路径规划问题。
崔瀛[1]等人研究了在物流配送中采用蚁群算法的一种数学模型;田劲松[2]使用蚁群算法设计了一种测量控制网TSP 问题的求解方法并得出了计算结果;王玉富[3]提出了一种多配送中心的蚁群算法模型,并使用K均值聚类算法进行了研究;陈世欢[4]等人通过蚁群算法对航班路径规划进行了研究;李霄玉[5]等人提出了一种在NSGA-Ⅱ基础上加入局部搜索策略的自适应算法。
观光车作为特种设备,常用于景区中运输游客。某景区通过观光车运送旅客至景区内的各个景点,并根据实际需要停留一定时间。与传统的TSP 问题不同,其存在以下差异:
1)起始点是固定的,在蚁群初始化时均在起始点生成。
2)观光车到达各节点时,存在停留时间。
3)求解的并非是最短路径,而是遍历整个节点所需的最短时间。
传统的蚁群算法并未对节点的停留时间进行考虑,在计算时是否考虑停留时间将对结果产生巨大影响。本文采用了一种基于时间因子的改进蚁群算法,通过与传统蚁群算法进行比较,在考虑遍历节点时存在停留时间的情况下,取得了较好的结果。
1 问题背景
某景区采用观光车运送旅客,N个景点之间路线为完全图,观光车从景区1 号景点出发,可自行选择行驶至任意下一个景点,最终遍历完景区内的每一个景点。根据景点的不同情况,观光车在每个景点需停留不同的时间,问题为:求解观光车的行进路线(路径),使得在遍历完整个景点的情况下所用的时间最短。
2 模型建立
设景区内景点的集合为N,在不考虑各节点的停留时间时,求解上述关于路径距离的最小值,用式(1)表示:
其中,di,j表示第i个节点到第j个节点的距离,arrivedi,j表示i、j之间的距离,各节点之间的距离矩阵用式(2)表示:
显然,当i=j时,di,j=0,则上述距离矩阵可转化为式(3):
进一步,在考虑观光车在各节点的停留时间时,将各节点的停留时间表示为时间因子,见式(4):
其中,ti表示各节点应停留时间。基于各节点的时间因子,对距离矩阵式(3)中元素采用式(5)进行处理:
其中,v代表车辆行驶速度,上述式(3)转化为式(6)所示的形式:
根据式(3)~式(6),上述式(1)最终转化为求解tmin的方程,见式(7):
其中,tmin表示观光车在遍历完全部景点后所用的最短时间。
3 算法步骤与实现
3.1 算法步骤
1)对蚂蚁种群进行初始化,使生成的蚂蚁全部位于起始点(1 号节点),启动遍历程序。
2)生成已访问节点表、待访问节点表(allow),某时刻蚂蚁向下一个节点转移的期望用启发函数ηi,j表示,路径上的信息素浓度用τ表示,启发函数用式(8)表示:
某时刻t,蚂蚁从i节点转移到j节点的转移概率pi,j(t)用式(9)表示:
式中:
α,β——启发因子系数;
τi,j(t)——t时刻位于节点i、节点j之间的路径上信息素浓度;
τi,s(t)——t时刻位于节点i至目标点s的信息素浓度;
ηi,s(t)——蚂蚁在t时刻位于节点i、目标点s之间的转移期望程度;
ηi,j(t)——蚂蚁在t时刻位于节点i、节点j之间的转移期望程度。
3)采用轮盘赌方式,选择转移概率最大的节点作为下一个即将访问的节点,随即对已访问节点表(allow)进行更新。
4)蚂蚁遍历完成所有节点后,取出路径表,并在每次迭代完成后计算出最短时间及路径表。
上述过程如图1 所示。
3.2 算法实现
由于算法中大多采用矩阵记录相关信息,针对该特点本算法采用Matlab 编程实现,关键步骤如下:
1)载入各节点间距离矩阵(distance)。
2)根据时间因子矩阵:times=(t1t2···tN)及式(5)生成距离矩阵(Distance)。
3)参数定义及赋值见表1。
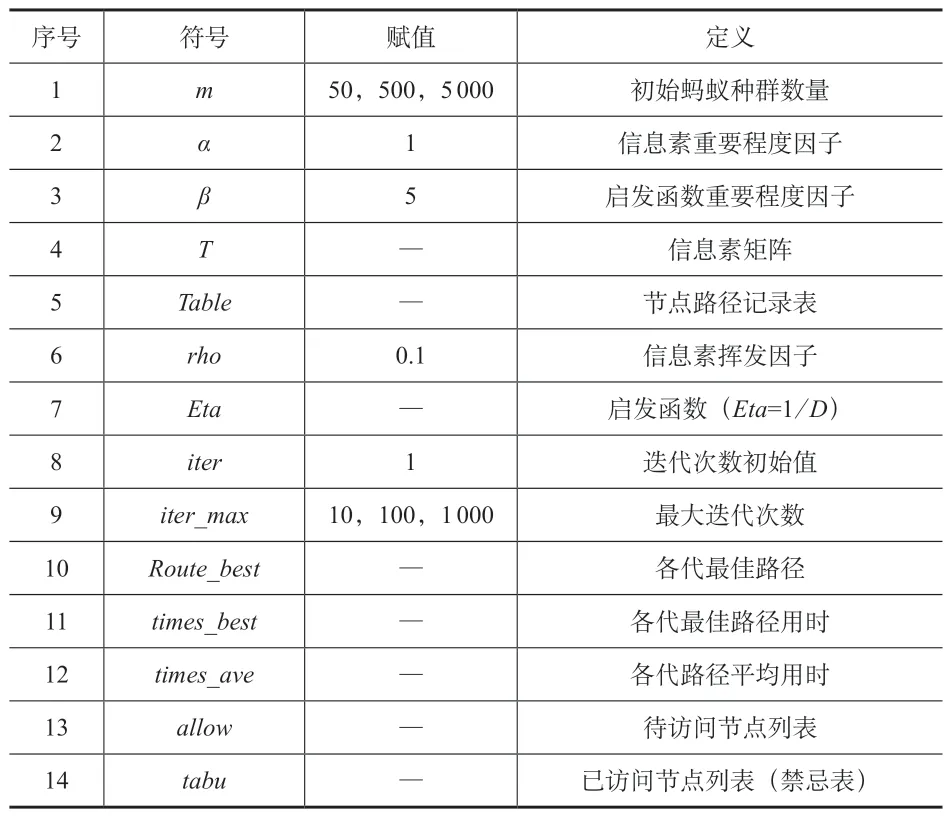
表1 参数定义表
4)初始节点设置为1 号节点,将蚁群初始化后定位初始生成位置为该节点。将该位置放入节点路径记录表并建立节点索引。
5)逐个蚂蚁、逐个节点进行以下循环:
记录已访问节点列表(禁忌表)→生成待访问节点列表→用式(9)计算下一个节点的转移概率→采用轮盘赌方法选择下一个即将访问的节点。
6)上述循环完成后,取出每个蚂蚁的路径并计算路径用时与路径平均用时,同时更新信息素,进行下一次迭代。
7)迭代完成后,取出各代最佳路径用时与各代路径平均用时,计算结束。
4 结果分析
以某景区实际问题为例,景区内停站景点(节点)为31 个,每个景点的停车时间见表2,各景点位置坐标化后如图2 所示。
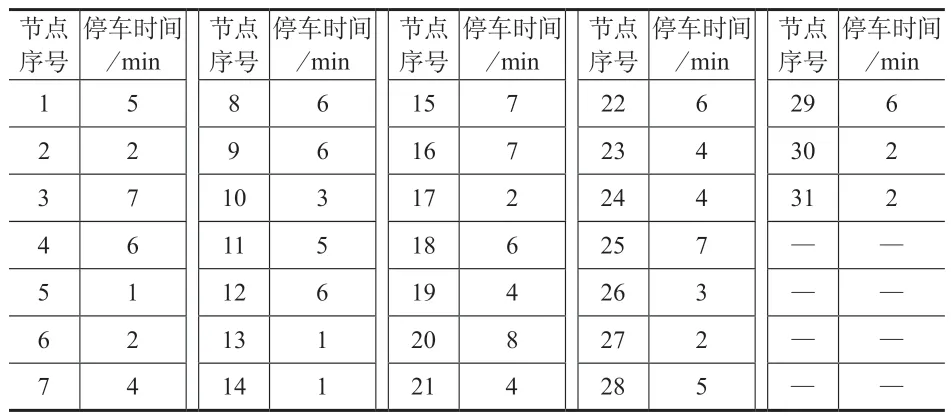
表2 节点时间因子赋值表
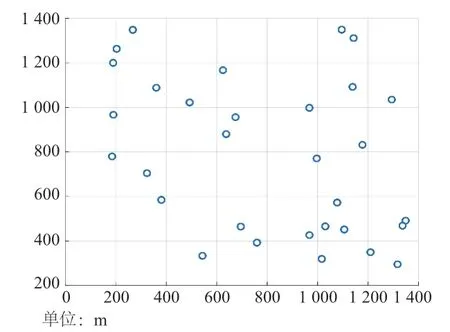
图2 各景点位置坐标图
种群初始化时,对蚁群的数量依次赋值为50、500、5 000 个,并分别迭代10、100、1 000 次,通过引入时间因子参与计算,求得最短遍历时间及路径,见表3。迭代至最短路径(时间)时,迭代次数与用时(最短用时、平均用时)关系如图3 所示。迭代至最短路径(时间)时,路径表如图4 所示。
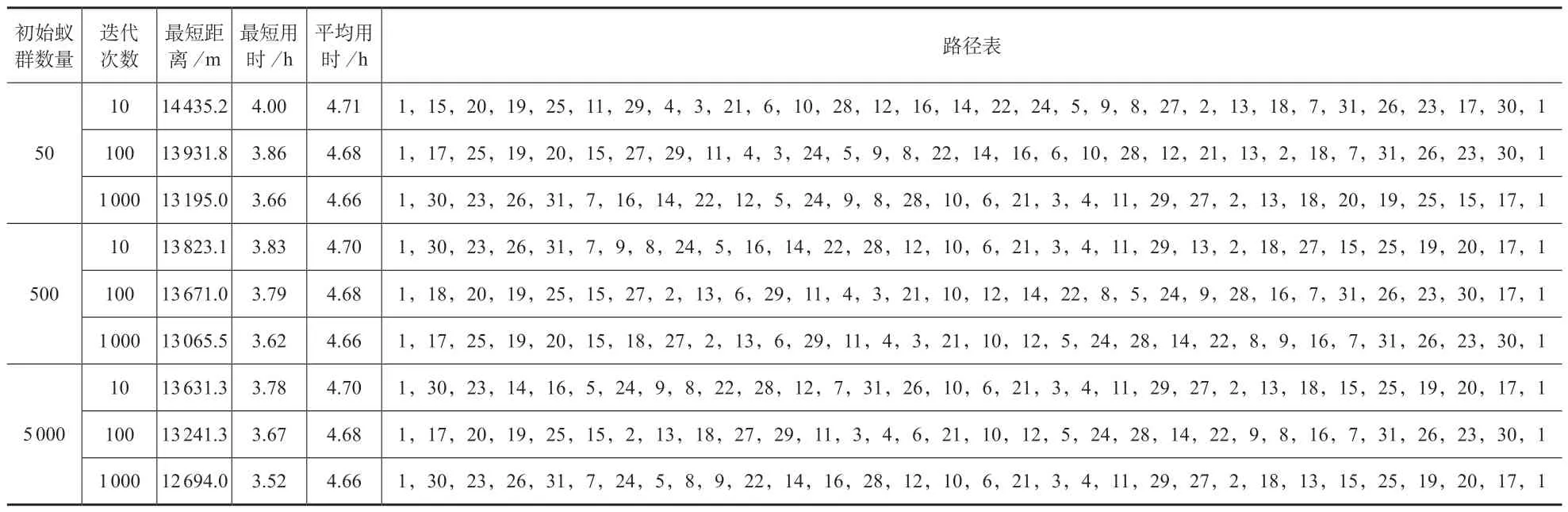
表3 计算结果统计表

图3 不同种群及迭代次数时平均用时与最短用时图(续)
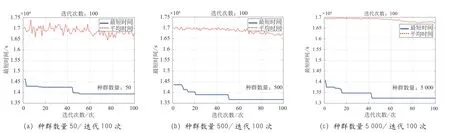
图3 不同种群及迭代次数时平均用时与最短用时图

图4 不同种群及迭代次数时产生的最优路径图
由上述结果可见,采用随机遍历的方式通过所有节点,其平均用时约为4.6 ~4.7 h。采用基于时间因子的蚁群算法最短用时为3.5 ~4.0 h,最大程度节约时间达24.5%。同时,初始蚁群总量对结果的影响较大,但初始蚁群总量确定后,迭代次数较少即可达到收敛,体现了算法的优越性。
5 结束语
本文采用一种改进的蚁群算法对景区内观光车运行路径规划问题进行了研究,通过引入一种特定的时间因子,改进了原始距离矩阵表。通过增加种群数量及迭代次数,计算结果改善较为明显,改进的算法能更好地适应特定条件下增加的路径规划需求。

