自适应安全的支持模式匹配的流加密方案

李一鸣,刘胜利

(1.上海交通大学 计算机科学与工程系,上海 200240;2.密码科学技术全国重点实验室,北京 100878)

1 引 言

随着大数据时代的到来,人们基于海量用户数据开发出了功能丰富的应用。在某些应用场景中,可能需要对采集到的数据进行模式匹配操作,即检测某个关键字是否出现在某条数据中,或者是出现在数据的哪些位置。如深度包检测 (Deep-Packet Inspection,DPI)、关键词热度分析、基因组数据检索和数据库数据检索等,都可能使用到模式匹配。在这些场景中,数据的模式匹配操作可能由一个不被数据发送者信任的第三方(提供服务的厂商)来执行。如果这些数据,特别是包含了用户隐私的数据,都以明文的方式提交给第三方进行处理,必然会有隐私泄露的风险。如果对明文数据进行加密后发送,第三方又无法对其进行模式匹配操作,从而无法提供服务。因此,如何在不影响模式匹配功能的同时为用户提供隐私保护,成为了一个需要解决的问题。

目前对这一问题的解决思路主要集中于研究(对称版本或公钥版本)可搜索加密方案 (Searchable Encryption,SE)[1-3]。但是,根据文献[3],现有的可搜索加密方案在应用的灵活性上仍存在一些局限:① 部分可搜索加密方案需要提前固定待检测关键字集合,如果出现新的关键字,就需要重新配置系统,因此不适用于关键字频繁更新的场景;② 部分可搜索加密方案要求关键字是某个固定的长度,如文献[4],而这在真实的应用场景中很难满足;③ 部分可搜索加密方案只能用于判断关键字与消息是否匹配,而无法给出具体匹配的位置,如文献[2,5];④ 部分可搜索加密方案无法支持带通配符的模式匹配,如文献[4,6];⑤ 部分可搜索加密方案只能处理固定长度的消息,如文献[5];这些方案需要等待所有消息输入完毕后一起打包加密,且消息长度需满足方案设置;相比之下,比较理想的情况是能够对任意可变长度的数据流进行处理。

2 支持模式匹配的流加密方案

为满足更灵活的应用需求,文献[3]提出了带有可调整陷门的可搜索加密 (Searchable Encryption with Shiftable Trapdoors,SEST) 方案。SEST方案允许第三方自由选择关键字,而无需在加密前给定关键字集合;支持更灵活的关键字长度以及待匹配消息长度;可以给出关键字出现在消息中的所有位置,而不仅仅是“是否匹配”这一比特的结果。特别地,文献[7]将支持任意待匹配消息长度的模式匹配的方案叫作支持模式匹配的流加密方案(Stream Encryption supporting Pattern Matching,SEPM)。SEPM的语义和安全性定义与文献[3]中的基本一致。文中采用文献[7]中SEPM的叫法。

文献[3]给出了配对群上基于交互式通用Diffie-Hellman (interactive General Diffie-Hellman,i-GDH) 假设的SEST构造方案。该方案支持无通配符的模式匹配,满足选择安全性(文献[3]中还给出了一种更强的安全性定义——自适应安全性,并没有实现自适应安全性)。在此基础上,文献[3]又给出了支持带通配符模式匹配的SEST方案,同样实现了选择安全性。除了对明文信息的保护外,文献[6]进一步考虑如何对关键字进行保护。文献[6]给出了配对群上基于i-GDH假设的公钥版本流密文模式匹配方案AS3E。该方案同时具有选择安全性和关键字不可区分性,但只支持不带通配符的模式匹配。文献[6]提出了一种分段技术,用于支持任意长度的消息加密。文献[7]提出了配对群上基于i-GDH假设的SEPM方案。该方案具有选择安全性、支持带通配符的模式匹配。与已有方案相比,文献[7]中的方案在效率方面进行了提升。注意到,前述方案都依赖于i-GDH假设,该假设是一个交互式安全假设,目前其困难性仅在一般群模型(Generic Group Model,GGM)下有分析[8],因此i-GDH并不是一个很理想的安全假设。为了改进这一点,文献[7]提出了基于一种非交互式安全假设的SEPM方案。

目前,尚没有SEPM构造能够同时满足基于非交互式安全假设实现,具有自适应安全性,以及支持带通配符的模式匹配。此外,随着量子算法的兴起,基于离散对数家族假设和大整数族假设的密码方案在量子攻击下将丧失其安全性,因此密码学界对如何设计后量子密码算法进行了大量研究,并在诸多领域取得了成果,如文献[9-12]。然而,目前仍然没有能够抵抗量子攻击的SEPM方案。

笔者针对上述问题进行了研究,提出了新的SEPM方案,能够基于非交互式后量子假设证明自适应安全性,且支持带通配符的模式匹配。文中以支持匹配函数的函数加密方案 (Functional Encryption,FE)为组件,提出了一个SEPM的通用构造。该通用构造具有自适应安全性,且支持带通配符的模式匹配。进一步结合已有的基于容错学习 (Learning With Errors,LWE) 假设的FE实例化方案[13-14],文中得到了基于LWE假设的SEPM实例化方案。其中,LWE假设是非交互式安全假设,且是广泛认可的抗量子攻击的安全假设,因此基于LWE假设的SEPM实例化方案具有抗量子攻击的可能。表1给出了文中SEPM通用构造及其实例化与现有SEPM方案的比较。

表1 文中SEPM方案与现有方案的比较

3 预备知识

3.1 符号约定

3.2 支持模式匹配的流加密方案

(1) 初始化算法Setup(1κ,L):输入安全参数κ∈N,关键字长度上限L∈N+,输出公开参数P。

(2) 密钥生成算法KeyGen(P):输入公开参数P,输出一对主公私钥(Kmpk,Kmsk)。

(3) 密钥派生算法Issue(Kmsk,W):输入主私钥Kmsk以及长度为任意≤L的关键字W=(w1,…,w)∈,输出陷门TW。

(5) 测试算法Test(TW,W,C):输入陷门TW、关键字W以及密文C,输出匹配集合⊆[n]。

支持模式匹配的流加密方案具有以下性质:

(Match(W,S[k,k+-1])=1)⟹(Pr[k∈]=1-negl(κ)) 。

(2) 可忽略错误接收。可忽略错误接收要求对于任意k∈[n],如果S和W在k处不匹配,那么k以极大概率不在中,即∀k∈[n],有

(Match(W,S[k,k+-1])=0)⟹(Pr[k∈]=negl(κ)) 。

3.3 函数加密方案

(1) 初始化算法Setup(1κ,λ):输入参数κ,λ∈N,输出公开参数P。

(2) 密钥生成算法KeyGen(P):输入公开参数P,输出一对主公私钥(Kmpk,Kmsk)。

函数加密方案具有以下性质:

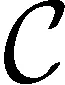
3.4 BCC20消息分段技术

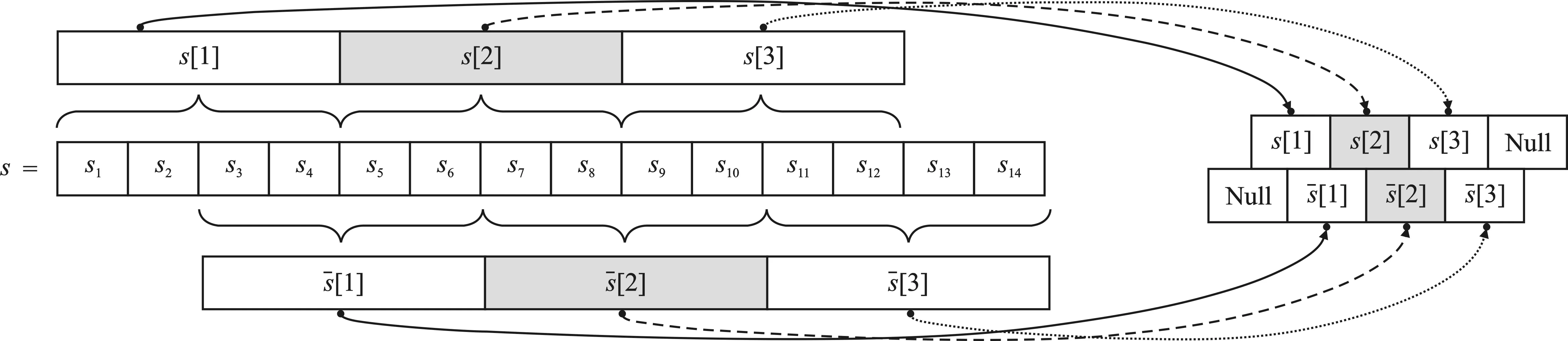
图1 BCC 20分段技术示例,取n=14,L=2,nl=4,ns=2,nf=3

(1) 存在ι∈[nf],使得(ι-1)nl+1≤k≤ιnl-+1,此时子串S[k,k+-1]落在Sι段。

(2) 存在ι∈[nf],使得ns+(ι-1)nl+1≤k≤ns+ιnl-+1,此时子串S[k,k+-1]落在段。

证明:易知,S的所有长子串为S[1,],S[2,+1],…,S[n-+1,n]。首先证明对于任意子串S[k,k+-1],一定能找到满足(1)或(2)要求的ι∈[nf]。因为≤L,所以对于任意ι∈[nf],有ιnl-+1=(ι-1)nl+nl-+1≥(ι-1)nl+nl-L+1=ns+(ι-1)nl+1 以及ns+ιnl-+1=ιnl+(L-)+1≥ιnl+1成立。进而可得

[(nf-1)nl+1,ns+(nf-1)nl+1]∪[ns+(nf-1)nl+1,n-+1]=[n-+1] 。

所以可知,任意k∈[n-+1]一定落在某个区间[(ι-1)nl+1,ιnl-+1]或者[ns+(ι-1)nl+1,ns+ιnl-+1]中。对于任意k∈[n-+1],如果(ι-1)nl+1≤k≤ιnl-+1,那么有k≥(ι-1)nl+1,且k+-1≤ιnl。又Sι=S[(ι-1)nl+1,ιnl]=(s(ι-1)nl+1,…,sιnl),可知S[k,k+-1]一定包含在段Sι内。同理可证,如果ns+(ι-1)nl+1≤k≤ns+ιnl-+1,那么子串S[k,k+-1]一定包含在段内。由此可证,S的任意一个长子串一定落在某一个段或者偏移段内。

4 基于FE的SEPM通用构造方案

文中介绍如何使用FE通用构造SEPM,并基于LWE假设对SEPM通用构造进行实例化。

4.1 SEPM通用构造方案

(1) 初始化算法P←Setup(1κ,L):调用算法Fe.Setup(1κ,2L)→P,并返回公开参数P。

(2) 密钥生成算法(Kmpk,Kmsk)←KeyGen(P):调用算法Fe.KeyGen(P)→(Kmpk,Kmsk),并返回公私钥对(Kmpk,Kmsk)。

(3) 密钥派生算法TW←Issue(Kmsk,W),其中W=(w1,…,w)∈

① 对任意d∈[0,2L-],置*2L。

② 对任意d∈[0,2L-],构造函数fWd∈2L,其中fWd(S)∶=Match2L(Wd,S)。

③ 对任意d∈[0,2L-],调用算法Fe.KeyDer(Kmsk,fWd)→KWd。

④ 返回陷门TW∶=(KW0,…,KW2L-l)。

(4) 加密算法C←Enc(Kmpk,S),其中S=(s1,…,s)∈n：

① 计算nl∶=2L,ns=L,nf=(n-ns)/nl。

② 对任意i∈[nf],置段Si=S[(i-1)nl+1,inl],调用Fe.Enc(Kmpk,Si)→Ci。

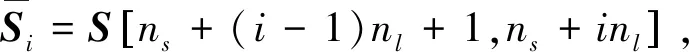
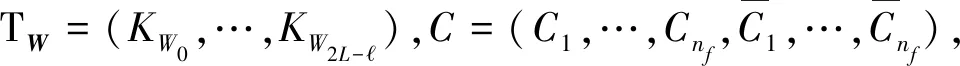
② 对任意i∈[nf]以及任意d∈[0,2L-],如果Fe.Dec(KWd,Ci)=1,计算k∶=(i-1)nl+1+d,置∶=∪{k}。

③ 对任意i∈[nf]以及任意d∈[0,2L-],如果计算k∶=ns+(i-1)nl+1+d,置∶=∪{k}。

(1) 初始化算法Setup仅调用1次Fe.Setup,其时间复杂度为tSetup=t′Setup。

(2) 密钥生成算法KeyGen仅调用1次Fe.KeyGen,其时间复杂度为tKeyGen=t′KeyGen。

关于SEPM的通用构造方案Sepm,有如下定理成立。

定理1如果Fe是支持匹配函数族的自适应安全的函数加密方案,那么通用构造方案Sepm具有正确性、可忽略错误接收以及自适应安全性。

4.2 SEPM通用构造方案的正确性和可忽略错误接收证明

证明(正确性):下证对任意关键字W=(w1,…,wl)∈S和消息S=(s1,…,sl)∈n,如果S和W在k∈[n]处匹配,有Pr[k∈]=1-negl(κ)。对于任意k∈[n],S和W在k处匹配等价于Match(W,S[k,k+-1])=1。易知S[k,k+-1]是S的一个长度为≤L的子串。根据引理1可知,S[k,k+-1]一定在某个段或者偏移段内,假设S[k,k+-1]落在段Sι=S[(ι-1)nl+1,ιnl]内,即(ι-1)nl+1≤k≤ιnl-+1(如落在偏移段内,可类似证明)。计算S[k,k+-1]在段Sι内的偏移量为Δ=k-(ι-1)nl-1,且0≤Δ≤nl-。可知

又根据SEPM通用构造方案Sepm中Issue算法的设计,有

易知, Match2L(WΔ,Sι)=Match(W,S[k,k+-1])=1 成立。进而由FE方案Fe的正确性可知,Fe.Dec(KWΔ,Cι)=fWΔ(Sι)=Match2L(WΔ,Sι)=1以1-negl(κ)概率成立。根据方案Sepm的设计,如果Fe.Dec(KWΔ,Cι)=1,那么k′∶=(ι-1)nl+1+Δ=k会被加入集合T中,所以Pr[k∈]=1-negl(κ)。方案的正确性得证。

证明(可忽略错误接收):下证对任意关键字W=(w1,…,wl)∈S和消息S=(s1,…,sn)∈n,如果S和W在k∈[n-+1]处不匹配,有Pr[k∈]=negl(κ)(根据构造,当k∈[n-+2,n],S和W在k处不匹配且k不会被加入集合)。使用反证法,假设S和W在k∈[n-+1]处不匹配,但是k∈以不可忽略概率成立,证矛盾。如果k∈,根据构造一定有ι∈[nf],Δ∈[0,2L-]使得k=(ι-1)nl+1+Δ且Fe.Dec(KWΔ,Cι)=1,或k=ns+(ι-1)nl+1+Δ且设k是通过第1种情况被加入到集合中的,即k=(ι-1)nl+1+Δ且Fe.Dec(KWΔ,Cι)=1(如果是第2种情况,可类似证明)。设Sι是密文Cι对应的明文消息段,有

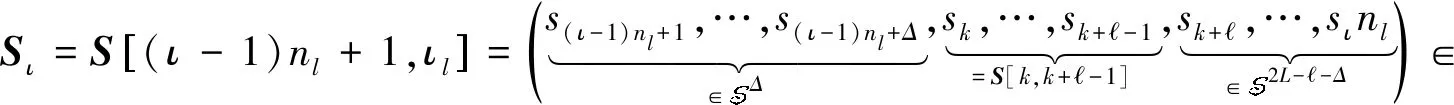
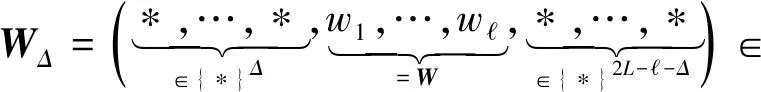
因为S和W在k处不匹配,所以Match(W,S[k,k+-1])=0,进而Match2L(WΔ,Sι)=0。基于此,如果k∈以不可忽略概率成立,就以不可忽略概率找到WΔ和Sι,使得Fe.Dec(KWΔ,Cι)=1≠fWΔ(Sι)=Match2L(WΔ,Sι)=0,这与Fe的正确性矛盾。方案的可忽略错误接收得证。

4.3 SEPM通用构造方案自适应安全性证明

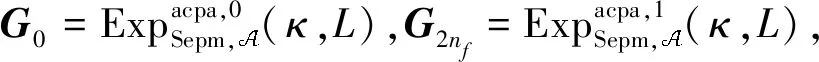
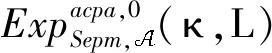
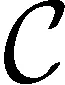
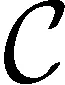
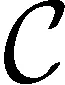
下证,如果Fe是安全的,那么两两相邻实验Gj-1和Gj,j∈[2nf],之间就是计算不可区分的。

引理2对任意j∈[2nf],有|Pr[Gj⟹1]-Pr[Gj-1⟹1]|≤max

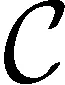
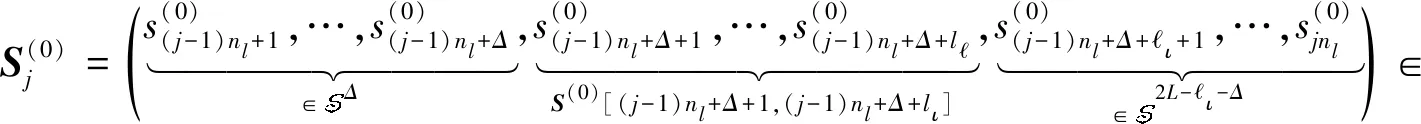
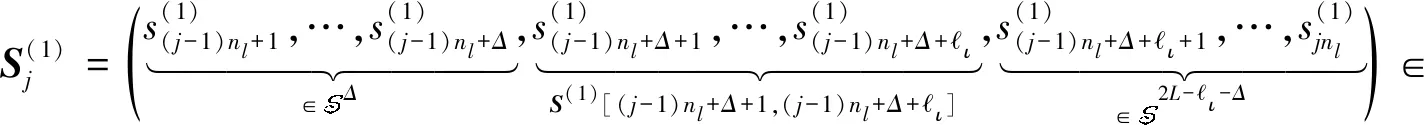
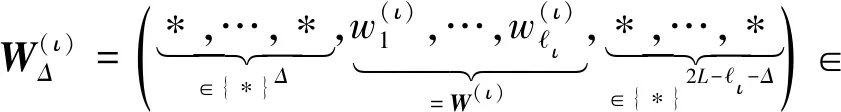
易知,有Match(W(ι),S(1)[(j-1)nl+Δ+1,(j-1)nl+Δ+ι])=1且Match(W(ι),S(0)[(j-1)nl+Δ+1,(j-1)nl+Δ+ι])=0成立。由此可知W(ι)与S(1)在(j-1)nl+Δ+1处匹配,但是与S(0)在(j-1)nl+Δ+1处不匹配,这与是合法敌手矛盾。所以,如果是合法敌手,那么也是合法敌手。综上,如果合法敌手能够以不可忽略的概率区分实验Gj和Gj-1,那么就可以以同样的优势打破FE的安全性,所以引理得证。

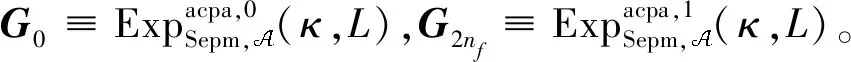
|Pr[G0⟹1]-Pr[G2nf⟹1]|≤∑i∈[2nf]|Pr[Gi-1⟹1]-Pr[Gi⟹1]|≤

2nfmax

4.4 SEPM通用构造方案实例化

本节介绍如何基于LWE假设对4.1节中的SEPM通用构造方案Sepm进行实例化。

根据文献[16],对于任意n,m=poly(κ),q≤2poly(n),χ是参数为σ的离散高斯分布,且2n1/2≤σ≤q,<=q,求解判定性LWE-{n,q,chi,m}问题至少与求解最坏情况汇报格上的困难问题GapSVP_gamma和SIVP_gamma一样难,其中渐进参数γ=O(nq/σ)。这些格上的困难假设是公认的可抵抗量子攻击的,因此,LWE假设也是广泛认可的抗量子攻击假设。

文献[13-14]分别提出了基于LWE假设的支持任意多项式大小电路的自适应安全的FE。易知对任意λ=poly(κ),模式匹配函数λ是多项式大小电路可实现的。使用文献[13-14]中的FE实例化方案对4.1节中的SEPM通用构造方案Sepm进行实例化可以得到基于LWE假设的SEPM实例化方案。事实上,在对SEPM通用构造进行实例化时,只需要使用支持匹配函数族的自适应安全的FE作为组件。但遗憾的是,目前尚没有针对这种函数族的满足要求的FE实例化方案,因此文中使用了支持更通用函数族的FE实例化方案。但是这样会使得最终的SEPM实例化方案在效率方面的表现不尽如人意。如果后续能够有满足实例化要求的更高效的FE实例化方案,那么相应地,套用文中的SEPM通用构造,就可以得到更高效的SEPM方案。

5 结束语

笔者基于LWE假设提出了具有自适应安全性的、支持带通配符模式匹配的SEPM方案。具体地,以支持匹配函数的FE作为组件,提出了SEPM的通用构造方法,该通用构造具有自适应安全性且支持带通配符的模式匹配。通过对FE组件进行实例化,进一步得到了基于LWE假设的SEPM实例化方案。但是因为FE组件实例化的局限性,文中SEPM的最终实例化在效率方面仍有待提升。如何构造效率更高的满足实例化要求的FE是一个值得进一步研究的问题。