基于时空网络模型的灭火救援路径优化方法
管 宁
(青岛市崂山区消防救援大队,山东 青岛 266000)
目前,对生产生活威胁最大的仍然是火灾。对城市来说,无论是生产企业还是大型住宅小区,因为设备和人员密集,一旦发生火灾,就可能导致不可估量的生命和财产损失。因此,一旦发生火情,快速及时地进行救援工作势在必行[1]。在灭火救援工作中,救援队伍反应的实时性、灭火救援所配置的装备都直接关系到救援工作的效率。其中,对灭火救援成败影响最关键的还有救援路径的设计和选择,这直接影响灭火救援工作的进度和准确性[2]。无论是生产企业还是大型住宅小区,因为设备配置和建筑结构具有复杂性,并且火情爆发后形成各种未知性和复杂性,所以灭火救援路径出现选择障碍[3]。采用合理的算法对灭火救援路径进行设计和规划,对灭火救援工作的顺利开展具有十分重要的意义。该文采用时空网络模型构建灭火救援路径的优化方法,以期在灭火救援工作中找到更好的切入点。
1 灭火救援路径优化的时空网络模型构建
以一个大型园区为例,一旦发生火灾,会出现一个或多个火情点。将灭火救援所需的人员、设备和物资运送到这些火情点,是灭火救援路径设计和优化工作的核心任务。但是,因为园区内各种障碍的存在、火情带来的未知性和复杂性,使灭火救援的人员、设备和物资配送,成为有约束条件限制下的有限空间内的优化问题。这样,灭火救援路径的设计和优化就成为有限时间和有限空间内的优化,所以采用时空网络模型是非常有针对性的。
时空网络模型是同时考虑时间约束条件和空间约束条件,将优化问题看作一个同时包括时间维度和空间维度的二维网络优化模型,再充分考虑其他约束条件完成优化过程得到最佳的解决方案。
对该文的灭火救援工作来说,就是要在最短的时间内以最短路径完成灭火救援所需的人员、设备、物资的配送,因此构建时空网络模型如公式(1)所示。
式中:R为所有可能的灭火救援路径上的点的集合;ri为灭火救援路径上第i个点;rj为灭火救援路径上第j个点;T为灭火救援所有时间点的集合;ti为救援时间点集合中第i个时间点;tj为救援时间点集合中第j个时间点;Trirjki为灭火救援车辆在从i点到j点完成行驶所需要的时间;tw为新的决策时间点。
在公式(1)所示的时空网络模型中,涉及2 个决策变量,第一个决策变量如公式(2)所示。
在公式(1)所示的时空网络模型中,第二个决策变量如公式(3)所示。
至此,构建了在最短时间内以最短路径完成灭火救援的时空网络模型。
2 灭火救援路径优化模型的求解
构建灭火救援路径的时空网络优化模型后,如何对模型求解关系到路径优化的效率和效果。因为涉及多约束、多目标优化,时空网络模型采用一般方法进行求解很难达到预期效果,所以该文采取基于遗传算法的求解策略。
遗传算法本身是从生物学领域借鉴过来的一种智能优化算法,在随机巡游的过程中遵循生物种群基因序列进化的各项操作,并且带有一定的元启发特点,对该文的灭火救援路径优化求解具有很好的适应性。在遗传算法的优化过程中,更优的路径方案被保留下来,一直到最优的路径方案生成。任何可能的救援路径方案将成为时空网络模型的初始解,也就是遗传算法的初始种群,进而按照遗传算法的交叉、变异、选择等操作处理,得到进化后的最优解,相应的处理流程如图1 所示。

图1 遗传算法求解灭火救援路径时空网络模型的流程
从图1 中可以看出,采用遗传算法完成灭火救援路径时空网络模型求解的流程:第一步,根据灭火救援路径优化的实际问题,构建时空网络优化模型,形成对实际问题的抽象化和数学建模。第二步,根据各种约束条件、各优化目标进行染色体编码设计,形成从实际问题到遗传算法的对应。第三步,根据火灾现场的实际火情情况,根据时空网络模型中可能的各种救援路径方案,随机生成救援路径的初始解,即灭火救援路径的初始方案。第四步,根据灭火救援路径形成的初始种群,进行遗传算法的适应度计算,如果适应度计算的结果满足遗传算法的终止条件,则将当前的灭火救援路径方案输出,从而解决了对应的实际问题,算法结束。第五步,如果适应度函数的计算结果没有满足遗传算法的终止条件,则按照遗传算法的选择、交叉、变异三项操作进行种群进化,生成下一代种群,再次重复第四步的操作。如果第四步一直不能满足算法终止条件,则反复执行第五步、第四步,直到算法终止条件得到满足。
为了便于说明遗传算法的操作处理过程,这里给出一个具体的实例。
假设火灾救援现场有2 个救援中心,那么这2 个救援中心,分别用1、2 两个数字进行表示。同时,现场发现了15个火情点都需要救援,延续救援中心的编码排列,那么从3~17 这样15 个数字分别表示15 个火情点。按照遗传算法的第三步,随机生成一个救援路径的初始解,如图2 所示。

图2 实例中的初始救援路径方案
在图2 中,初始救援路径方案形成了10-9-8-12-4-14-6-13-7-16-11-15-17-5-3 的救援顺序。假设火灾救援过程中共投入了一、二、三、四一共4 组救援力量,那么根据时空网络模型以及遗传算法的处理,得到的救援方案如下。第一组救援力量:救援中心1-火情点10-火情点9-火情点8-救援中心1。第二组救援力量:救援中心2-火情点12-火情点4-火情点14-火情点6-救援中心2。第三组救援力量:救援中心1-火情点13-火情点7-火情点16-火情点11-火情点15-救援中心1。第四组救援力量:救援中心2-火情点17-火情点5-火情点3-救援中心2。
可见,救援中心1 负责第一组救援力量和第三组救援力量的输送,并为这两组救援力量配置了合理的优化路径。救援中心2 负责第二组救援力量和第四组救援力量的输送,并为这两组救援力量配置了合理的优化路径。
3 灭火救援路径优化测试试验
为了验证该文提出的灭火救援路径时空网络模型及遗传算法求解方案的正确性和有效性,进一步展开灭火救援路径优化的测试研究。仍然按照前文实例的配置原则,设定2个救援中心、15 个火情点,并按照1,2,3,……,17 的方式排列。根据时空网络优化模型的配置原则,首先要给15个火情点X、Y两个决策变量配置需求量表,见表1。
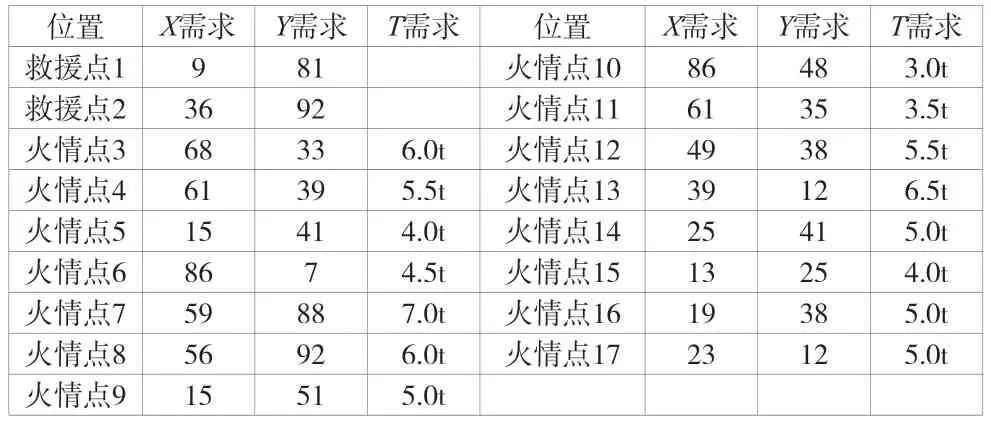
表1 15 个火情点决策变量的需求量表
在表1 中,给出了各个火情点的需求,其中T表示所需的救援水量的需求。在这样的需求下,按照该文构建的遗传算法进行求解,得到的救援路径配置方案如图3 所示。

图3 测试试验中得到的灭火救援路径配置方案
对应于图3 的救援路径配置方案,各救援车辆的路径以及需求配置见表2。
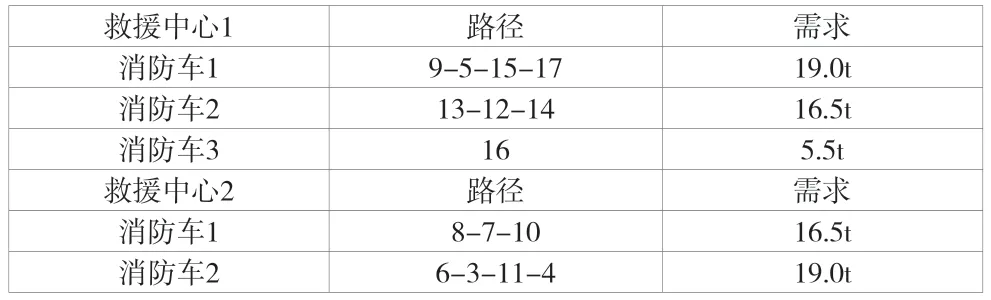
表2 各救援车辆的路径及需求配置满足情况
综合图3 和表2 的结果,可以看出:从救援中心1 出发的消防车一共有3 辆,其中:消防车1 的灭火救援路径是火情点9-火情点5-火情点15-火情点17,可以满足4 个火情点的19t 水量需求;消防车2 的灭火救援路径是火情点13-火情点12-火情点14,可以满足3 个火情点的16.5t 水量需求;消防车3 的灭火救援路径是火情点16,可以满足1个火情点的5.5t 水量需求。
从救援中心2 出发的消防车一共有2 辆,其中:消防车1 的灭火救援路径是火情点8-火情点7-火情点10,可以满足3 个火情点的16.5t 水量需求;消防车2 的灭火救援路径是火情点6-火情点13-火情点11-火情点4,可以满足4 个火情点的19t 水量需求。
按照类似的方法,设定10 组仿真案例,其救援路径的优化效果见表3。
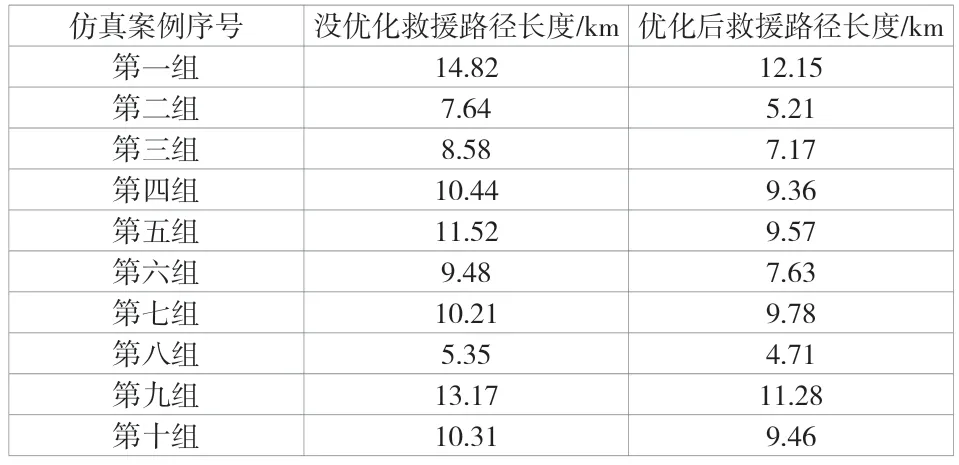
表3 10 组仿真案例的救援路径优化结果
为了便于表3 中优化结果的直观展示,将其绘制成柱状图,如图4 所示。
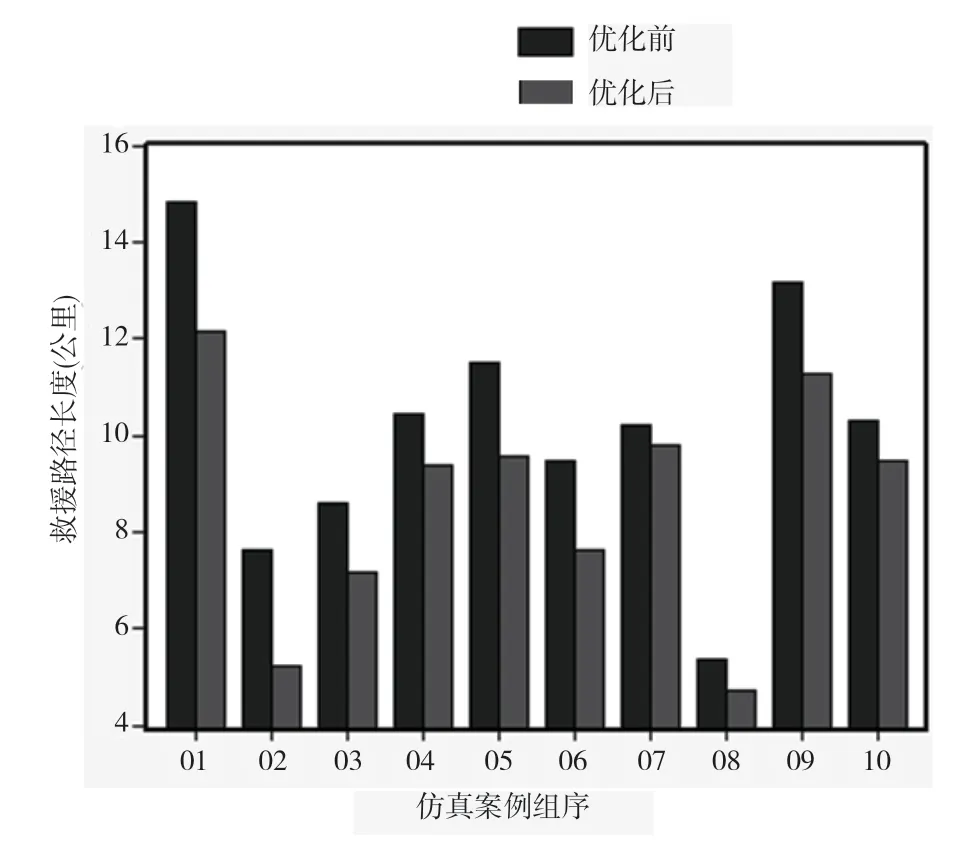
图4 表3 中结果的柱状图显示
图4 中,横坐标为仿真案例的组序,纵坐标为救援路径的长度,单位是公里。从图中的结果可以看出,经过该文方法提出的优化模型获得的救援路径优化结果,10 组案例的路径长度都有明显缩短,从而提升了救援效率。
4 结论
火灾仍然是生产生活的重要威胁,如果处理不当或救援不及时将导致重大的生命和财产损失。该文中以灭火救援路径优化方法为核心研究内容,首先从救援时间和救援距离2 个约束出发,构建了灭火救援路径的时空网络模型。针对时空网络模型,进一步提出基于遗传算法的灭火救援路径优化方案,在给出具体的求解流程以后进一步给出了一个实例,阐述遗传算法求解过程中的编码设计、初始种群生成、对应灭火救援实际问题的求解过程。在灭火救援路径优化的测试试验中,配置了2 个救援中心和15 个火情点,在构建时空网络模型后采用遗传算法进行路径优化和求解,2 个救援中心分别派出了3 辆消防车和2 辆消防车,不仅得到了各个火情点的合理救援路径,也能满足各个火情点的救援水量需求。

