含临界尺度颗粒月壤的钻进负载特性分析
赵德明 王贺 高兴文 胡明


摘 要: 為了解决月壤钻探取样过程中所存在的由临界尺度月壤颗粒导致负载异常的问题,从试验与离散元仿真两方面研究钻具在含临界尺度颗粒月壤中的负载特性,揭示临界尺度月壤颗粒与钻具的作用机理,以期为钻进规程制定和月壤机械性质反演等提供支撑。结果表明:临界尺度颗粒运移特性与钻进负载具有强关联性。临界尺度颗粒半径越大,偏置距离越小,钻头负载越大,对应的工况就越危险;临界尺度颗粒的形状对负载的大小及变化趋势影响不大,但会增加负载曲线的波动幅度,使钻具抖动。钻具卡钻和堵钻现象主要由临界尺度颗粒与钻具的伴随运动导致,偏载现象由临界尺度颗粒在钻具周围的螺旋运动导致;其中,颗粒在钻具周围伴随运动的幅度受颗粒长径比变化影响,长径比较大时会导致钻具负载波动剧烈。
关键词: 月壤;临界尺度颗粒;钻进负载;运移特性;离散元方法
中图分类号: V19 文献标志码: A 文章编号: 1673-3851 (2023) 03-0254-09
引文格式:赵德明,王贺,高兴文,等.含临界尺度颗粒月壤的钻进负载特性分析[J]. 浙江理工大学学报(自然科学),2023,49(2):254-262.
Reference Format: ZHAO Deming, WANG He, GAO Xingwen, et al. Analysis of the drilling load in lunar soil with critical size particles[J]. Journal of Zhejiang Sci-Tech University,2023,49(2):254-262.
Analysis of the drilling load in lunar soil with critical size particles
ZHAO Deming, WANG He, GAO Xingwen, HU Ming
(School of Mechanical Engineering, Zhejiang Sci-Tech University, Hangzhou 310018, China)
Abstract: To address the loading anomalies caused by critical-scale lunar soil particles during lunar soil drilling and sampling, we investigated the payload of drilling tools in lunar soil containing critical size particles from both experiments and simulations and revealed the mechanism of interaction between critical size lunar soil particles and drilling tools, in the hope of providing support for the formulation of drilling procedures and the inversion of lunar soil mechanical properties. The results show that the critical size particle transport properties are highly correlated with the drilling load. The bigger the critical particle radius is, the smaller the offset distance is; the bigger the bit load is, the more dangerous the corresponding working condition is. The shape of the critical scale particles does not have a significant impact on the size and change trend of the load but will make drilling tool shake by increasing the fluctuation of the load curve. The jamming and plugging of drilling tools are mainly caused by the accompanying motion of the critical size particles and the drilling tools, and the off-loading phenomenon is caused by the spiral motion of the critical size particles around the drilling tools. Specifically, the amplitude of the accompanying movement of particles around the drilling tool is affected by the change of the particle length-diameter ratio, and when the length-diameter ratio is large, the load of the drill tool will fluctuate violently.
Key words: lunar soil; critical size particles; drilling load; transport properties; discrete element method
0 引 言
月球土壤钻探取样(月壤钻进取样)是月球探测项目的重要组成部分。苏联Luna 20探测器在钻进过程中发生钻进故障,最终仅取得0.05 kg月壤样品,且Luna 24探测器在钻进过程中也因负载过大而多次报警[1]。临界尺度月壤颗粒的粒径与取样作用器具执行末端[2]尺度相近。相比性质较稳定的月尘与月岩,临界尺度月壤颗粒的粒径和分布随机性更强,对钻进取样活动的影响也更大。在探月钻进取样过程中,钻具因临界尺度月壤颗粒导致的故障模式主要有以下3种:a)临界尺度月壤颗粒出现在钻头的正前方,堵塞取样口,导致钻具丧失取样能力,破坏原有的钻头钻进排屑条件,致使负载急剧增加;b)临界尺度月壤颗粒出现在钻头的侧前方,对钻具刃具产生冲击载荷,破坏刃具结构,同时导致钻头偏载,进而使得钻杆弯曲,严重时导致钻杆整体失效;c)与钻进区域相邻的临界尺度颗粒刮擦、破坏软质钻杆螺旋结构,导致钻具排屑失效[3]。
在月壤钻进取样的研究中,大多数研究人员通过模拟月壤在地面上进行实验,如:Li等[4]开展了月岩取心钻头钻进特性研究;Liu等[5]和肖洪[6]比较了不同钻头结构对钻进过程的影响。以上文献的研究重点在于探究钻具结构对钻进取样的影响,由于月球环境的特殊性,需要对钻进过程进行负载分析,判断钻进故障产生原因,进而改进钻进工况。地面试验无法实时观测到月壤内部的动态变化过程,但可以借助离散元方法(Discrete element method,DEM)揭示这些问题,如Hasan等[7]和Bui等[8]通过DEM进行了月壤的建模和特性研究,Cui等[9]和Zhao等[10]进行了月壤的钻探和取样研究。
本文为研究含临界尺度颗粒月壤的钻进力载特性,对钻头钻进切削区进行了失效力载分析,开展了多工况的钻进负载试验,并在此基础上建立了月壤钻进的仿真模型,通过仿真分析了含临界尺度颗粒月壤的钻进负载特性,探究了临界尺度月壤颗粒的形状、位置等信息对钻进负载的影响规律,为后续钻具的回转速率、进尺速率等钻进规程的制定以及月壤的内摩擦角、抗剪强度和内聚力等机械性质的反演提供依据。
1 失效力载分析
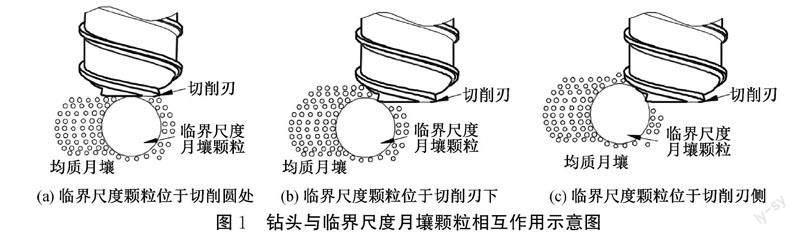
为简化钻头切削刃与临界尺度月壤颗粒间的复杂受力关系,本文将钻头与临界尺度月壤颗粒间的回转切削模型简化为直线切削模型。直线切削失效模型是描述切削刃与切削对象间力载关系的最基本模型,可使用库伦提出的经典土力学中的极限平衡理论来求解。McKyes等[11]通过引入切削刃构型影响对月壤与钻具间的极限平衡理论进行修正,发现钻具切削月壤过程存在两种模型:单楔角与双楔角模型的切削模型。切削区域内月壤的失效形式也分为单楔形失效和双楔形失效,本文切削刃对应失效形式为双楔形失效。图1为钻头切削刃与临界尺度月壤颗粒相互作用的3种工况。
为分析钻头单切削刃与临界尺度月壤颗粒相互作用的负载特性,本文建立了月壤失效力学模型。直线切削模型对应的切削刃前端双楔形失效区分为两个部分:中心失效区和侧向失效区。在建立临界尺度月壤颗粒受力平衡方程前提出以下几点假设:a)切削过程中,失效区的月壤微元沿切削刃的前刀面及失效区月壤内某一滑动面运动;b)失效区月壤微元为刚体,仅考虑微元受到的外部作用力,忽略微元自身的内部间的相互作用力;c)切削过程中,失效区月壤微元处于极限平衡状态。失效区钻头切削刃与临界尺度月壤颗粒的受力分析如图2所示。
对临界尺度月壤颗粒进行受力分析,可列如下平衡方程:
其中:chRp为侧向失效区的力载影响;FX、FY分别表示临界尺度月壤颗粒水平和垂直方向分力;P表示月壤对等效切削刃前刀面的力,F表示月壤对等效切削刃后刀面的力;α表示钻具切削角;表示月壤与切削刃间摩擦角;β表示失效角;δ表示月壤内摩擦角;q表示切削区覆土平均压力;c表示月壤内聚力;dc表示颗粒偏置距离;dr表示切削影响区半径;G表示临界尺度颗粒及切削区月壤的重力;γ表示月壤容重,指单位容积内物体的质量;h表示切削深度。
在式(2)—(5)导致钻进失效的因素中,δ、、c由月壤的物理机械性质决定,F、Rc、h由钻具结构和钻进规程决定。月壤取样实践工程经验表明,当钻杆采用双螺纹结構时,主体结构采用旋转锥面的钻头更有助于排屑[12],因此试验所采用钻具选择空心外螺旋结构,其中钻头结构为旋转抛物面,双翼采用双螺纹矩形螺旋翼。钻头构型如图3所示,其中A与B分别表示钻头的切削圆和外包络圆。钻头与钻杆的具体结构参数如表1所示。在钻进规程和钻具结构确定的情况下,Rp、G与临界尺度月壤颗粒的大小相关,dc、α、β由临界尺度月壤颗粒的位置相关。月壤颗粒的典型形状主要有长条状、棱角状和次棱角状,经过长时间风化磨损后形状类似椭球状,钻头切削月壤失效分析中临界尺度月壤颗粒的形状为球形。颗粒的长径比是经过颗粒内部的最长径和与它相垂直的最长径之比,常用于描述颗粒形貌;为了探究形状对试验的影响,本文将临界尺度月壤颗粒的长径比也作为一个主要影响因素。因此,本文通过试验探究临界尺度月壤颗粒不同粒径、位置和长径比对钻进负载特性影响。
2 钻进负载特性试验
2.1 试验平台介绍
本文使用的多动能全参数钻取试验平台示意图如图4。测试平台上的高精度六维力传感器可以获得钻进过程中的钻压力、回转力矩和钻进速度的试验数据;钻进试验以中国地质大学研制的CUG-1A模拟月壤为对象,CUG-1A模拟月壤原料采用的是东北部吉林省辉南县新生代火山岩,CUG-1A的化学性质和物理力学性质与Apollo14采样点的月壤样品相似,是一种理想的低钛型月海月壤的模拟样品[13]。
2.2 试验方案
对于不同大小的临界尺度月壤颗粒,按照最优系数法将颗粒半径设置为4个梯度:6.3、10.0、16.0 mm和25.0 mm。对于不同位置的临界尺度月壤颗粒,将半径为16.0 mm的月壤颗粒设置4种工况:偏钻头中轴线7.5 mm位置、偏钻头中轴线15.0 mm位置、偏钻头中轴线22.5 mm位置、偏钻头中轴线30.0 mm位置。对于不同形状的临界尺度月壤颗粒,利用球形度的概念[14]来描述一般性非球(凸体)颗粒的形状:
其中:VP和AP分别为颗粒的体积和表面积;0≤ψ≤1,球体对应于ψ=1。本文采用4种不同长径比的椭球颗粒来探究月壤颗粒形状对钻进负载的影响。根据式(6)计算出4种颗粒的球形度,依次为:0.69、0.78、0.89、0.93。4种椭球颗粒的等体积直径为16.0 mm,长径比分别设为:1∶4、4∶1、1∶2、2∶1。4种椭球颗粒如图5所示。
为准确地验证临界尺度颗粒对钻进负载特性的影响,试验在模拟月壤制备过程中定点设置临界尺度颗粒。模拟月壤制备完成后,通过控制钻具位置实施定位钻取。首先将烘干处理后的CUG-1A模拟月壤放置在月壤桶内,并堆积到准备放置临界尺度颗粒的高度,桶高400.0 mm,堆积模拟月壤高度200.0 mm。按预定位置放置好临界尺度颗粒并压实,在上方继续放置制备好的模拟月壤至预设高度。控制钻具运行到模拟月壤表面,设置钻具回转速度18 r/min,进尺速度 60 mm/min。
2.3 试验结果分析
以临界尺度月壤粒径为变量,4种粒径的临界尺度颗粒的钻进负载曲线如图6所示。当试验采用钻具切削圆直径为30.0 mm时,由图6可见,当颗粒直径小于切削圆直径时,钻进压力F和扭矩TZ增加平缓不受影响。当粒径增加至32.0 mm,略大于切削圆时,钻进压力剧烈增加至70.0 N,钻进扭矩也明显增大,这说明此时钻具正前方遇到较大颗粒时发生了堵钻,同时可以看出钻进压力对大颗粒的响应要比钻进扭矩更为敏感。当钻具正前方遇到超大尺度颗粒(≥50.0 mm)时,钻进压力和扭矩均快速响应剧烈增加,其中钻进压力峰值达到700.0 N,说明超大颗粒对钻具影响最为严重。
以临界尺度月壤偏置距离为变量,对直径为16.0 mm的临界尺度颗粒在4种位置的钻进负载进行分析,结果如图7所示。试验采用钻具外包络圆半径为30.0 mm,因此当钻具遇到偏置距离小于30.0 mm的颗粒时,钻进负载一定會增加。钻具遇到偏置30.0 mm处的颗粒时,钻进压力从5.0 N增加到30.0 N,钻进扭矩值也从先从0.1 N·m增加大2.5 N·m,之后负载又恢复正常水平,说明颗粒与钻具发生接触后被挤压到钻具外围。钻头半径为30.0 mm,颗粒偏置距离为45.0 mm时,钻进压力略微增大而钻进扭矩不受影响,当颗粒偏置距离为60.0 mm时对钻进负载没有任何影响,说明月壤取样过程中钻具的影响域半径小于自身半径的1.5倍。
以临界尺度月壤形状为变量,不同长径比颗粒的钻进负载曲线如图8所示。4种颗粒位姿与所处位置均相同,可以看出钻具遇到4种颗粒时钻进压力增大到20.0~60.0 N,钻进扭矩增大到0.3~0.9 N·m。增大的幅度不能看出明显差别,而增大趋势是颗粒大小与所处位置共同决定,因此颗粒形状只对钻进负载增加值的大小有所影响,并不是负载变化的决定性因素。
综上可知:临界尺度颗粒直径小于切削圆直径时,钻进压力和扭矩增加平缓不受影响,临界尺度颗粒直径半径越大,钻头负载越大,当粒径大于钻具切削圆半径时,发生堵钻;偏置距离越小钻头负载越大,对应的工况就越危险,当偏置距离大于钻具切削圆半径的1.5倍时,钻具负载不再受临界尺度颗粒影响;临界尺度颗粒的形状虽然不会影响负载的大小以及趋势但会增加负载曲线的波动幅度使钻具抖动。
3 钻进负载特性仿真分析
试验只能得到负载的大致规律;为了揭示负载产生机理,本文建立了DEM仿真模型,仿真不仅能获得钻进过程的负载信息,还能实时观测到月壤内部的动态变化过程,可以进一步分析临界尺度颗粒对负载的影响机理。仿真模型中涉及的月壤颗粒包括两类,一是临界尺度月壤颗粒,其余大部分是月壤细颗粒。临界尺度月壤颗粒定义是直径与取样作用器具执行末端尺度相近的大颗粒,本文对临界尺度取值为0.1D~1.0D(即6.0~60.0 mm),与钻杆外径尺寸相近。仿真参数优化后的月壤颗粒参数设置如表2所示。含临界尺度颗粒月壤的钻取DEM仿真模型如图9所示。试验方案设计了12种试验工况,仿真条件与试验相同,仿真试验初始状态如图10所示。
以临界尺度月壤粒径为变量时,4种不同大小的临界尺度颗粒的钻进负载曲线如图11所示,当颗粒粒径小于仿真钻具切削圆直径时,仿真负载平缓增加。随着颗粒粒径的增大,钻进压力和钻进扭矩均迅速增大。以临界尺度月壤偏置距离为变量时,4种不同位置的临界尺度颗粒的钻进负载曲线如图12所示,偏置距离大于仿真钻具外包络圆半径时,钻进压力和钻进扭矩不受影响。而当偏置距离小于仿真钻具外包络圆半径时,钻进压力发生较大波动,钻进扭矩在某一段钻进深度出现迅速增加后恢复平缓增加。以临界尺度月壤形状为变量时,4种不同形状的临界尺度颗粒的钻进负载曲线如图13所示,负载增加趋势平缓,但负载出现明显的波动现象。受限于仿真计算规模,无法实现和试验条件完全对等的仿真,仿真中负载的绝对数值与试验数值存在差异,但负载变化趋势与试验负载数据一致,且一致性较好。
不同仿真工况下的临界尺度月壤颗粒钻取过程的运移轨迹如图14—16所示,图中A点为轨迹起点,B为终点。仿真结果表明,临界尺度颗粒在钻取过程的流动特征分为3类运动情况:第一类是直径小于切削圆的颗粒,进入取样管内发生螺旋运动,如图14(a)、图14(b);第二类是直径大于切削圆的颗粒位于钻头正前方或者距钻头中轴线7.5 mm以内时,会卷进钻头前端造成堵塞,随着钻头向下钻进,如图14(c)—(d)和图15(b);第三类是距钻头中轴线大于等于7.5 mm的临界尺度颗粒,会在钻具的螺旋作用下向外运移呈螺旋上移的运动轨迹,如图15(a)、图15(c)和图16(a)—(d)。
临界尺度月壤颗粒的运移轨迹结果表明,临界尺度颗粒月壤在钻取过程的运动轨迹分为3类:一是进入取样管内做螺旋运动;二是发生堵钻,随钻头做直线运动;三是随着钻具螺旋翼螺旋上移。其中:第二类运动轨迹的颗粒是引起负载变化的主要原因,且当临界尺度颗粒直径大于切削圆直径时,会发生堵钻、卡钻等现象;第三类运动轨迹的临界尺度颗粒会引起负载波动和钻头偏载等故障。
临界尺度颗粒的运移特征与宏观钻进负载特性间具有强相关性。第一类运动轨迹对应的钻进负载平稳增加不受影响;第二类运动轨迹对应的钻进负载剧烈增加并发生卡钻,并且钻进压力比钻进扭矩的响应更为敏感;第三类运动轨迹对应的钻进负载增加并发生波动后恢复正常,当颗粒形状发生变化时,负载的波动现象更为明显。
4 结 论
本文针对月壤钻进取样过程中由临界尺度月壤颗粒导致的钻进负载异常问题,以单切削刃与临界尺度月壤颗粒相互作用力学平衡条件为基础,建立了临界尺度月壤颗粒切削失效力学模型。在钻具构型参数和钻进规程确定的前提下,以临界尺度颗粒的大小、位置和形状为变量,采用控制变量法设计了多组试验,得到各因素对负载的影响规律,并进一步通过仿真分析了临界尺度颗粒与钻具的力载作用机理。主要结论如下:
a)临界尺度颗粒半径越大,偏置距离越小,钻头负载越大,对应的工况就越危险。临界尺度颗粒的形状对负载的大小以及趋势影响不大,但会增加负载曲线的波动幅度使钻具发生抖动,进而影响取样效果。
b)临界尺度月壤颗粒在钻取过程的运移状态主要分3类:一是进入取样管内与样品做螺旋运动;二是在取样口前端堵钻,与钻具做直线运动;三是运移到钻具侧向并随排屑做螺旋式上移运动。
c)取样管内临界尺度月壤颗粒对负载影响轻微,钻头前端较大颗粒会导致负载急剧增加并卡钻,侧向随排屑运动月壤颗粒会导致负载波动,波动幅度与颗粒长径比正相关。
d)临界尺度月壤颗粒直径大于30.0 mm(切削圆直径)的会造成堵钻现象。偏置量小于1.5倍钻杆半径(45.0 mm)的临界尺度月壤颗粒会引起钻进负载的变化。
参考文献:
[1]鄢泰宁,补家武,吴翔,等.试论月球表面钻探取样的难点与关键技术[J].地质科技情报,2004, 23(4):12-14.
[2]郑永春,欧阳自远,王世杰,等.月壤的物理和機械性质[J].矿物岩石,2004, 24(4):14-19.
[3]魏广飞,王世杰,李雄耀.月球地形地貌对各种月面探测技术的影响[J].矿物学报,2013, 33(1):68-74.
[4]Li P, Jiang S Y, Tang D W, et al. Design and testing of coring bits on drilling lunar rock simulant[J]. Advances in Space Research, 2017,59(4):1057-1076.
[5]Liu T X, Zhou J, Liang L, et al. Effect of drill bit structure on sample collecting of lunar soil drilling[J]. Advances in Space Research, 2021, 68(1): 134-152.
[6]肖洪. 深层月壤取心钻头构型设计及其力载特性研究[D]. 哈尔滨: 哈尔滨工业大学, 2013: 24-42.
[7]Hasan A, Alshibli K A. Discrete element modeling of strength properties of Johnson space center (JSC-1A) lunar regolith simulant[J]. Journal of Aerospace Engineering, 2010, 23(3):157-165.
[8]Bui H H, Kobayashi T, Fukagawa R, et al. Numerical and experimental studies of gravity effect on the mechanism of lunar excavations[J]. Journal of Terramechanics, 2009, 46(3):115-124.
[9]Cui J S, Hou X Y, Wen G L, et al. DEM thermal simulation of bit and object in drilling of lunar soil simulant[J]. Advances in Space Research, 2018, 62(5):967-975.
[10]Zhao D M, Tang D W, Hou X Y, et al. Soil chip convey of lunar subsurface auger drill[J]. Advances in Space Research, 2016, 57(10):2196-2203.
[11]McKyes E,Ali O S. The cutting of soil by narrow blades[J]. Journal of Terramechanics,1977,14(2):43-58.
[12]博坤. 贯通式潜孔锤反循环钻进技术钻具优化及应用研究[D]. 长春: 吉林大学,2009: 39-69.
[13]贺新星, 肖龙, 黄俊, 等. 模拟月壤研究进展及CUG-1A模拟月壤[J]. 地质科技情报, 2011, 30(4): 137-142.
[14]肖渊甫,郑荣才,邓江红.岩石学简明教程[M]. 3版. 北京: 地质出版社,2009: 71-77.
(责任编辑:康 锋)
收稿日期: 2022-07-16网络出版日期:2022-12-02网络出版日期
基金项目: 国家自然科学基金项目(51805488)
作者简介: 赵德明(1986— ),男,辽宁辽阳人,讲师,博士,主要从事宇航空间机构方面的研究。
通信作者: 高兴文,E-mail:xwgao@zstu.edu.cn

