含沙水流对平面钢闸门底缘的冲蚀影响研究
杨良泽,蔡一平,许旭东,袁周致远,吉伯海
(1.河海大学 土木与交通学院,南京 210098;2.江苏省水利科学研究院,南京 210017)
平面钢闸门具有强度高、重量轻、结构简单等特点,被广泛应用于城市防洪和农田灌溉等,在水利行业中的作用日益凸显[1-2]。然而,工作闸门长期处于干湿交替的复杂水流环境,在动水启闭的过程中闸门底缘承受含沙水流的冲刷,不可避免地会出现腐蚀问题[3]。平面钢闸门的面板材料普遍为Q235,具有较好的塑性性能,但水中沙粒的硬度比钢材要大得多,在高速冲击过程中对面板的破坏主要表现为沿法向的塑性变形和沿切向的切削作用,致使防腐涂料和金属材料发生磨损、剥落,并进一步发生锈蚀[4-5]。随着冲蚀的长时间累积,闸门构件截面厚度逐渐变薄,甚至出现腐蚀坑洞,进而可能引发强度破坏、结构失稳和振动失效等问题[6]。
冲蚀磨损是指夹杂在流体中的颗粒对材料表面进行冲击所造成的一种材料损耗现象。相关学者通过试验和有限元数值模拟研究了沙粒直接撞击金属表面的影响规律,系统地分析了冲蚀角度、冲蚀速率和颗粒数的改变对金属材料表面微观形态的影响[7-10]。然而,含沙水流对闸门面板的冲蚀是一个宏观且复杂的流固耦合过程,由于影响因素多、水流环境复杂,难以通过试验模拟,并且有限单元法在对流项的离散处理方法及不可压流体原始变量法求解方面也不够成熟。因此,得益于计算流体动力学的快速发展,以有限体积法为数值方法的流体软件凭借其强大的计算内核和完善的理论模型,可通过模拟真实流动来补充理论及试验的空缺[11]。PARSI等[12]对现有的冲蚀计算模型进行了总结,得出了影响冲蚀磨损的关键因素,并指出通过CFD进行冲蚀预测可以作为一种综合性方法。CHEN等[13-14]通过CFD仿真软件输流管道的流场和冲蚀影响分布进行了数值模拟,在考虑了固液两相耦合作用的基础上,分析了流速、颗粒含量和粒径等因素对冲蚀分布的影响。在水工结构方面,相关学者对水轮机和桥墩混凝土的冲蚀磨损进行了模拟,但对闸门冲蚀磨损的数值模拟研究较少[15-16]。由此可知,借助CFD对闸门面板在长期水流冲刷下的冲蚀磨损进行预测分析,是切实可行且具有创新意义的,可为平面钢闸门的防腐蚀设计提供参考,对提高闸门的使用寿命、保障泄水建筑物安全可靠的运行具有重大意义。
本文根据某在役平面钢闸门的工作环境,将闸门迎水面面板作为含沙水流的冲蚀对象,基于有限体积法建立流场模型,通过FLUENT软件进行数值模拟[17],选用Finnie模型预测闸门面板最大冲蚀率。通过控制变量法,分析了单因素影响下水流流速、沙粒直径和含沙量对闸门动水开启过程中面板冲蚀磨损分布的影响。
1 模型概况
1.1 模型参数
参照某蓄水闸工作门-露顶式平面钢闸门及其流场条件,于ANSYS WORKBENCH软件中建立几何模型,如图1所示。流场流向为X向,长度为15 m;跨度方向为Z向,宽度为6 m;高度方向为Y向。门前水体长10 m,高度h1为5 m;门体区域宽度t为0.54 m;闸后计算区域长4.44 m、高3 m。闸门开启的高度与闸前水头的比值为相对开度,实际工程中闸前水体巨大,开闸初期闸前水位变化不大,分别取0.05、0.1、0.15、0.2、0.25、0.3六种相对开度(e/h1)为计算工况,表示闸门提升的过程。通过对几何模型进行网格划分,得到有限体积法离散模型,然后导入FLUENT软件,设置流场、离散相和相关边界后进行初始化计算。图1中inlet、outlet分别表示流体和离散相进出口边界,其他均为固体壁面。
1.2 控制方程
1.2.1 连续相控制方程
连续相为恒温下的不可压缩流体,密度为998.2 kg/m3,黏度为0.001 003 Pa·s,不考虑能量耗散。控制方程包括质量、动量守恒方程,如式(1)、式(2)所示。外部流动简化为各向同性的均匀湍流,采用具有较好的稳定性、经济性和较高的计算精度的Standardk-ε模型预测湍流流场。
(1)
(2)
式中:p为静压;ρ为流体密度;t为时间;ui和uj分别为流体时均速度分量;τij为应力张量;gi和Fi分别为i方向上的重力体积力和外部体积力。
1.2.2 离散相模型
沙粒为石英砂,密度取2 600 kg/m3,由水体裹挟运动,体积分数小于10%,忽略颗粒与颗粒之间的相互作用、体积分数对连续相的影响,采用DPM离散相模型进行模拟。离散相的计算是在拉格朗日坐标下进行的,即以单个粒子为对象计算颗粒作用力方程,得出离散相颗粒运动轨迹,方程如下式
(3)
式中:u为流体速度;up为颗粒速度;FD(u-up)为颗粒单位质量曳力;L为流体动力黏度;CD为曳力系数;d为颗粒粒径;ρ为流体密度;ρp为颗粒密度;F为其他作用力;Re为颗粒雷诺数。
1.2.3 冲蚀计算模型
FULENT软件中默认的壁面冲蚀率计算公式为
(4)
式中:Rerosion为单位时间单位面积的质量损失,以下称冲蚀率;mp为粒子的质量流量;f(γ)为碰撞角度;v为粒子的撞击速度;b(v)为速度指数;C(dp)为粒子直径函数;Aface为壁面面积。
对于沙粒冲击碳钢而言,可采用Finnie模型预测冲蚀程度,该模型较好地解释了塑性材料在多角形磨粒、低冲击角下的磨损规律,计算式如下
(5)
式中:E为一个无量纲的质量;vp为颗粒的冲击速度;f(γ)为无量纲的冲击角度;n为指数,取值为2;k为碰撞返还系数,采用默认的返还系数1。
1.3 边界条件及初始条件
连续相进、出口边界条件分别设为速度入口和自由出流;壁面采用无滑移边界,选择标准壁面函数处理近壁区域,用近壁区域网格的 y+ 值判断计算结果的合理性。离散相进出口设置为逃逸,壁面设置为反弹;颗粒采用面射流源,颗粒初始速度与流体初始速度相同。需要注意的是,粒子与壁面发生碰撞时存在能量转化,颗粒的反射速度低于入射速度,所以模拟粒子与壁面的相互作用时需要设置法向和切向的回弹系数,而这种碰撞特征是由动量回弹系数描述。此处采用GRANT等[18]提出的颗粒碰撞恢复系数,分为法向反弹系数和切向反弹系数两部分,方程形式如下
(6)
式中:N和T分别为切向和法向;α单位为角度制。
计算中压力速度耦合采用 SIMPLE 算法,动量、湍动能的离散均采用二阶迎风格式。计算思路如下:首先在稳态条件下得到收敛的流场(残差为10-5),然后设置离散相与连续相双向耦合作用;注入颗粒后,连续相每10步迭代计算后进行离散相轨迹计算,然后将更新后的离散相动量与能量作为下一步的连续相方程计算的初始值,此后离散相轨迹与连续相流场交替计算,直到收敛稳定,最后把最大冲蚀速率作为分析冲蚀磨损影响的参考指标。
1.4 网格独立性验证
流场计算时存在颗粒流动,要求网格尺寸大于颗粒尺寸,否则可能造成计算振荡或非物理解。因此,在保证数值解的有效性的同时提高计算精度,需要适当加密网格。为确定数值模拟结果对网格数量的敏感程度,分别取0.08 m、0.1 m、0.15 m、0.2 m、0.25 m、0.3 m六种不同的网格尺寸,对同一模型进行六面体网格划分和参数设置,将计算所得的最大冲蚀率绘于图2。当网格尺寸大于0.2 m时,最大冲蚀率逐渐增大,离散性较大;当网格尺寸小于0.2 m时,网格数量相对较大,计算速度较慢,但最大冲蚀率的数值变化趋于稳定,且绝对值误差小于3%。因此,综合考虑计算精度和计算效率,选用网格尺寸0.15 m作为不同工况模型的网格划分标准。

图2 最大冲蚀率与网格尺寸的关系Fig.2 Relationship between the maximum erosion rate and mesh size
2 液-固两相特征分析
2.1 流场运动特征
基于离散相模型的冲蚀模拟,其颗粒的运动主要由连续相的流场特征决定,因此流体的运动特征分析是进行冲蚀研究的基础。如图3-a所示跨中截面动水压力流线分布,连续相流动初期为均匀流,流线各点的速度相同,过水断面形状和尺寸沿程不变,动水压强分布规律和静水压强分布规律一致。当流体经过闸门时,由于不规则边界造成断面收缩,导致水面突变,水流由均匀流变成急变流,此时动水压力急剧增大,最大值为1 045 295 Pa。这主要是因为固体边界发生改变后水头下降,部分重力势能转化为动能,使得水流速度增大,随之动压增大。进一步观察可知,水体流经闸门后,门体下游底部边界动压最大,而门后出现低压区,湍流强度逐渐变大,如图3-b所示。湍流强度是指脉动速度的均方根与时均速度的比值,由图可知,湍流强度最大值为483%。这可能是因为平坡闸下出流后发生水跃现象,水流从急流状态过渡到缓流状态,流速骤降。水跃区的水流上、下部两部分的交界面上流速梯度很大,紊动混掺强烈,液体质点不断地穿越交界面进行交换。

3-a 动水压力 3-b 湍流强度图3 流场特征Fig.3 Flow field characteristics
2.2 颗粒分布特征
在拉格朗日坐标下,流场中的第二相-沙粒被当作离散存在的一个个颗粒,基于上述流场变量求解每一个颗粒的受力状态,并获得粒子速度,进而追踪每一个颗粒的轨迹,如图4所示为计算完成时刻颗粒的位置分布及流向速度。沙粒从入口边界注射初期,由水流裹挟前进,速度保持不变,与闸门面板发生碰撞后速度减小,经过收缩断面时速度再次增大,最后由出口逃逸并被捕捉。

图4 颗粒的位置分布及流向速度Fig.4 Position distribution and flow velocity of particles
由上述分析可知,闸门面板在受到粒子的反复碰撞过程中,可能会发生塑性变形,促使表面涂层被逐步冲刷脱落,从而引发锈蚀。图5-a为相对开度为0.2时的闸门面板冲蚀率分布。由图可知,含沙水流对闸门面板的冲蚀作用主要集中于面板底部;冲蚀率随着沿Y轴高度的增加逐渐减小,在面板高度为1 m及以上的位置,冲蚀率已接近于零。为分析动水开启过程中面板底缘的冲蚀变化规律,进一步计算得到不同相对开度时的最大冲蚀率,如图5-b所示。随着相对开度逐渐增大,即平面闸门往上提升的过程中,含沙水流对面板底部的冲蚀作用逐渐减弱,且作用面沿中线对称分布,最大冲蚀率发生在面板左下角及右下角附近。当相对开度由0.05增至0.1时,相应的面板底缘最大冲蚀率由1.6×10-1kg/(m2·s)降至3.3×10-2kg/(m2·s),降幅为79.4%,较于其他阶段,冲蚀影响减弱的程度最大。由此可知,在闸门开启初期,受到含沙水流的冲蚀作用最为显著,若长期处于此种环境之下,闸门面板底缘可能会产生不同程度的冲刷破坏。

5-a 闸门面板冲蚀分布 5-b 最大冲蚀率图5 闸门开启过程中的最大冲蚀率Fig.5 The maximum erosion rate during the gate opening process2.3 面板冲蚀特征
3 影响因素分析
3.1 水流流速对闸门底缘冲蚀的影响
本节设定沙粒直径为0.5 mm,含沙量为1 kg/m3,通过改变连续相初始流速,研究闸门开启过程中位于不同相对开度时受到的冲蚀磨损作用。平原河流的流态稳定,水流速度较小,一般介于3~8 m/s,此处间隔1 m/s进行一次工况计算,得到各工况下的最大冲蚀率绘于图6-a。由上节分析可知,闸门提升各阶段的最大冲蚀率降幅差距较大,且数值较小,为清晰展示不同相对开度的最大冲蚀率的变化趋势,图6-a纵坐标数值选用对数坐标。对比发现,随着水流速度逐渐增大,闸门面板最大冲蚀率随之增大,两者的变化趋势可认为呈正相关。值得注意的是,水流速度由3 m/s增至4 m/s,并且闸门的相对开度由0.05提升至0.1时,最大冲蚀率降幅相近,对于其他流速的改变亦是如此,这可能意味着水流速度的改变对闸门提升过程中的最大冲蚀率增量的影响较小。
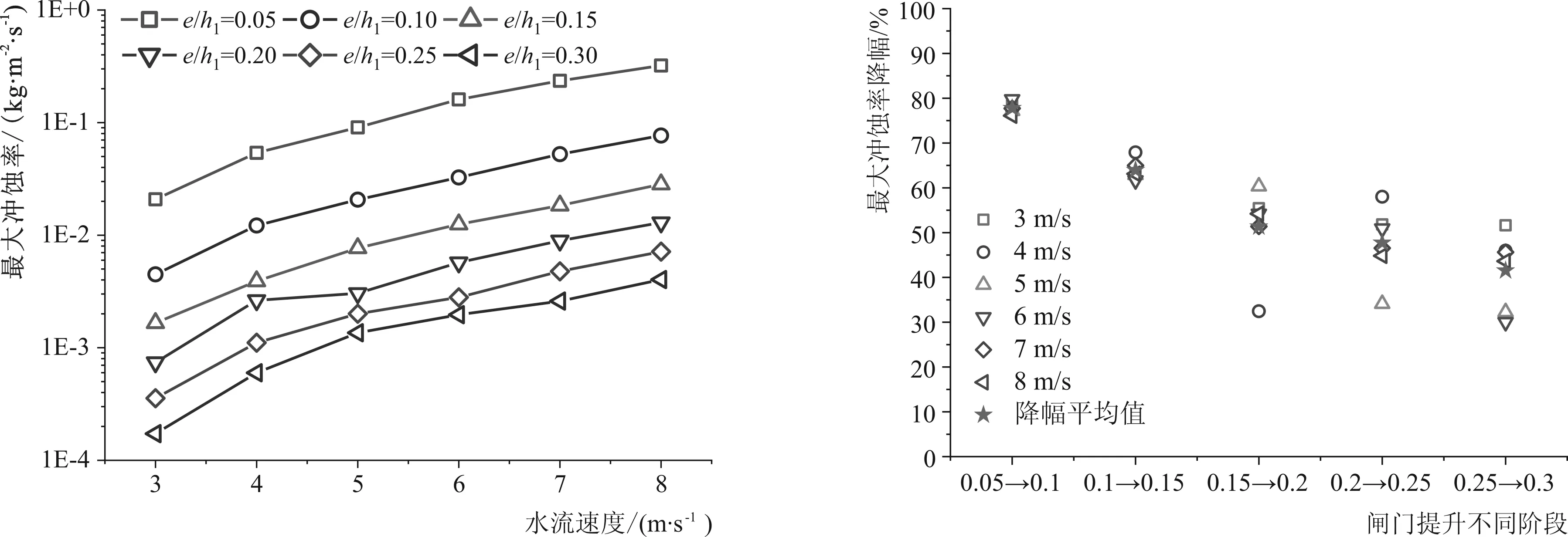
6-a 最大冲蚀率 6-b 最大冲蚀率降幅图6 水流速度对闸门面板的冲蚀影响Fig.6 Erosion effect of water velocity on gate panel
为验证上述推测,进一步处理数据,得到闸门提升不同阶段的最大冲蚀率降幅,如图6-b所示。对于同一提升阶段,不同水流速度下的最大冲蚀率降幅接近,但不同提升阶段的降幅百分比均值呈下降趋势。当相对开度由0.05升至0.1时,降幅最大,降幅百分比为78%,而降幅最小发生在0.25升至0.3阶段,降幅百分比为42%。由此可知,闸门开度越大,受到含沙水流的冲蚀越小。
3.2 沙粒直径对闸门底缘冲蚀的影响
文献[13]中指出颗粒粒径是影响冲蚀速度、冲蚀角度、有效撞击率的重要因素。因此,本节设定水流速度为8 m/s,含沙量为1 kg/m3,在河流沙粒粒径的分布范围内,选择0.075 mm、0.125 mm、0.25 mm、0.5 mm、0.75 mm、1 mm六种粒径工况,研究沙粒直径的改变对闸门面板底缘的冲蚀影响。如图7-a所示,最大冲蚀率随沙粒直径的增大整体上呈现出逐渐减小的发展趋势,两者的变化趋势可认为呈负相关。在一定的闸门开度下,最大冲蚀率在0.025 mm到0.5 mm的粒径范围内下降较为明显,当粒径大于0.5 mm后,降幅较小。这可能是因为在双向耦合的作用下,流体对直径较小的颗粒的携带性更好,使得颗粒以较大的动能冲击面板,进而冲蚀作用更加显著。此外,入口质量流量不变,当颗粒直径较小时,颗粒数目较多,能够增加沙粒和面板的有效碰撞面积,这同样扩大了冲蚀影响。计算闸门提升各阶段在不同粒径下的最大冲蚀率降幅见图7-b。由图7-b可知,最大冲蚀率降幅随着闸门提升而逐渐减小,这是由冲蚀作用面的位置决定的,与沙粒直径无关。在不同的提升阶段,不同粒径造成的最大冲蚀率降幅的离散性不同。相对开度较小时,颗粒在重力作用下主要集中于河道底部,闸门底缘冲蚀作用发展充分,因此数据离散性较小;当相对开度大于0.2后,闸门底缘较高,冲蚀影响较小,且粒径的改变会使主、次相之间的耦合作用发生变化,流场上层的颗粒运动更加随机,因此对于最大冲蚀率的预测离散性更大。

7-a 最大冲蚀率 7-b 最大冲蚀率降幅图7 沙粒直径对闸门面板的冲蚀影响Fig.7 Erosion effect of sand particle diameter on gate panel
3.3 含沙量对闸门底缘冲蚀的影响
含沙量是指水体单位体积中所含悬移质的泥沙重量,包含推移质和悬浮质的全部沙量,与水流挟沙力密切相关。数值模拟过程中,通过设定入口质量流量,在入口边界以面射入源的方式模拟河段下泄沙量,待颗粒注入后,连续相通过曳力及湍流影响粒子后续的运动状态。本节控制颗粒速度(8 m/s)和粒径(0.075 mm)不变,在0.25~1.5 kg/m3内,每隔0.25 kg/m3计算不同相对开度下的最大冲蚀率,结果见图8-a。由图8-a可知,闸门底缘最大冲蚀率随含沙量的增长而逐渐变大,两变量的相关系数约为0.99,呈完全正相关,可见含沙量对闸门底缘的冲蚀影响较大。含沙量越大,意味着有更多的颗粒参与磨损,与面板壁面碰撞得更加充分,随之冲蚀率变大。如图8-b所示,最大冲蚀率降幅随着闸门提升而逐渐减小,而且不同含沙量下的降幅百分比的离散性较小,表明闸门提升过程中所受到的冲蚀率降幅受含沙量影响较小。
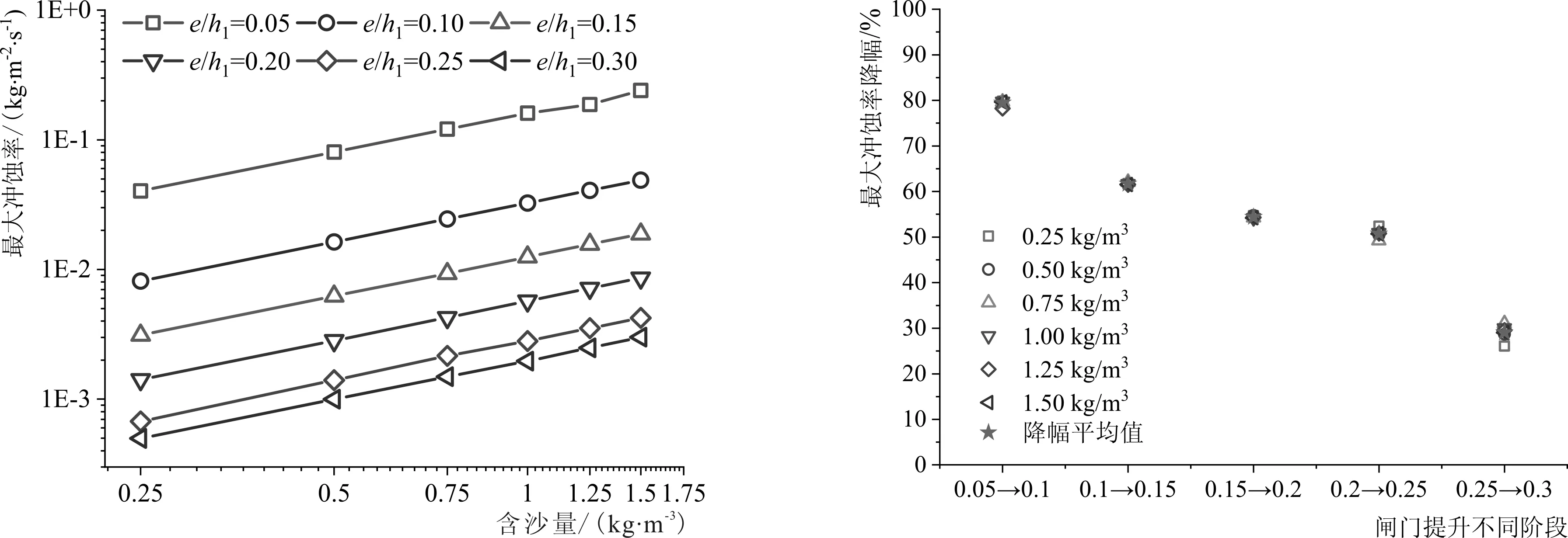
8-a 最大冲蚀率 8-b 最大冲蚀率降幅图8 含沙量对闸门面板的冲蚀影响Fig.8 Erosion effect of sand content on gate panel
4 结论
基于有限体积法建立流场模型,对平面钢闸门面板在开启过程中受到冲蚀磨损的动态过程进行了模拟,并探究了含沙水流的流速、含沙量和颗粒直径对闸门面板底缘的冲蚀影响规律,研究结果总结如下:(1)平面钢闸门提升过程中,含沙水流对面板底缘的冲蚀作用逐渐减小,实际工程中应避免门体长期处于低开度状态;(2)通过控制变量法,得出单因素影响下水流速度和含沙量与闸门底缘的冲蚀率呈正相关,是影响面板发生冲蚀破坏的的主要因素;而粒径的增大会使冲蚀率呈现减小的趋势;(3)闸门提升的不同阶段,其最大冲蚀率的降幅是一定的,开启初期降幅最大,随着开度越大而逐渐减小,受水流因素影响较小,这可为闸门确定最佳开启高度提供参考。

