基于数据驱动的催化重整产品质量预测

潘艳秋，张超阳，李鹏飞，俞 路

(大连理工大学化工学院，辽宁 大连 116024)

2022年,工业和信息化部印发了《“十四五”推动石化化工行业高质量发展的指导意见》,指出石化化工行业要推动产业结构调整、加快改造提升、提高行业竞争能力[1]。炼化企业可以通过信息智能化转型来开发提升产业竞争力的核心技术,助力炼化企业实现高效绿色化的增质提效[2-3]。

催化重整是生产石化原料和提升汽油质量的重要手段[4],全球约27%的汽油来自重整汽油、70%以上的芳烃来自重整芳烃、50%以上的炼油用氢来自重整产氢[5]。目前,针对催化重整装置的研究以对装置各单元进行建模和过程优化为主,如王连山等[6]针对某炼油厂连续催化重整过程提出了一种38集总组分动力学模型,并应用序列二次规划法(SQP)进行优化求解,最终可将芳烃收率提高0.17%。宋举业等[7]以中国石化洛阳分公司1.2 Mt/a连续催化重整装置为背景,建立了C4/C5分离流程模型,并对塔底温度和进料温度进行优化,实现降本增效达450万元/a。Askari等[8]利用Aspen HYSYS软件对炼油厂催化重整装置进行模拟,考察了原料组成、反应温度、反应压力对最终产品分布和汽油辛烷值的影响,结果表明该动力学模型准确,模拟方法有效。

由于催化重整加工过程机理十分复杂,重整装置具有时滞性强,操作参数高非线性、强耦合性特点,因而构建与实际运行状况高度一致的机理模型难度很大。随着互联网技术和大数据技术的快速发展,以神经网络为代表的数据驱动建模技术成为化工过程机理研究的重要手段[9]。例如,王杰等[10]以某炼化企业运行数据为基础,结合最大信息系数(MIC)法和Pearson相关系数法筛选出22个变量,基于BP神经网络建立了汽油研究法辛烷值(RON)预测模型,并采用遗传算法(GA)对模型参数进行优化,使重整汽油RON损失降低了25%。石翠翠等[11]针对特征变量存在高度非线性和冗余的特点,提出了一种基于偏最小二乘回归(PLS)和互信息(MI)组合降维的改进天牛须搜索算法(RSBAS)优化的BP神经网络模型(PLS-MI-RSBASBP),用于S Zorb装置汽油辛烷值预测。结果表明,相较于普通BP神经网络模型,该模型的预测性能更优秀。

然而,针对催化重整装置的数据驱动建模研究目前仍鲜有报道。基于此,本课题以国内某炼油厂催化重整装置实际运行数据为基础,通过设置数据筛选和处理规则构建BP神经网络数据驱动模型,用以预测重整装置苯产品中甲苯和非芳烃含量;进而通过实际应用效果对该模型进行评价,为后续全装置实时优化与平台模型集成提供技术支撑。

1 数据采集与处理

以某炼油厂连续催化重整装置为对象,按每1 h采集1次数据的频率,连续采集了其运行45 d的实时数据,共计1 000组数据。每组数据均包括流股流量、系统温度、流股组成共3类60个变量参数。其中部分关键数据如表1所示。由于通过实时监测系统获取的装置操作数据经常存在随机误差、仪表故障、记录错误等问题,而且部分变量间存在高度相关性,不能直接用于数据建模,因此需要进行数据处理以提高数据质量。

表1 部分变量数据采集结果

1.1 数据预处理

(1)数据初筛:①剔除恒为零的数据;②保留能够代表装置运行状况的变量。初筛后每组数据由60个变量减少为30个变量。

(2)显著误差校正:由于装置实时运行数据样本为正态分布或近似正态分布,故依据拉依达准则[12]进行数据显著误差检测和校正。

1.2 数据无量纲化处理

数据样本中不同变量的量纲和数据量级不同,无法直接用于建模分析,故采用线性无量纲法[13]中的极值法对数据样本进行无量纲化处理,在尽可能缩小各变量数据间数量级差异的同时保持变异系数尽量不变[14]。数据无量纲标准化处理方法见式(1)。

(1)

式中:x为原数据;x′为标准化后的数据;xmax与xmin分别为原数据的最大值与最小值。

1.3 变量相关性分析

基于重整装置运行过程的复杂性,装置实时变量数据之间存在高度非线性关系和强相关性。为避免冗余变量加大模型的计算量及模型臃肿性,需要筛选出与目标变量具有强相关性的变量作为模型输入变量。由于输入变量之间也存在强相关性,所以需要去除输入变量之间具有强相关性的变量,保证数据的高质量。常见的变量相关性分析方法有Pearson,Spearman,Kendall,MIC等[15],其中MIC方法适用范围更广、计算复杂度较低、鲁棒性较高[16-18],更适用于催化重整装置的变量相关性分析。MIC方法基于随机变量的n个观测值来计算,见式(2)。

(2)

式中:a、b分别是网格划分数量;B为最大网格数,式中B=n0.6[18];X,Y为基于网格的两个离散变量;I(X,Y)为互信息。其中,0≤MIC≤1;当MIC(X,Y)=0时,说明两个变量相互独立;当MIC(X,Y)=1时,说明两个变量线性相关。

1.3.1输入变量与目标输出变量间相关性分析

采用MIC法计算初步筛选后28个输入变量与2个目标变量间的相关性,结果如表2所示。其中MIC1和MIC2为各输入变量分别与目标输出变量1、2的MIC分析结果。

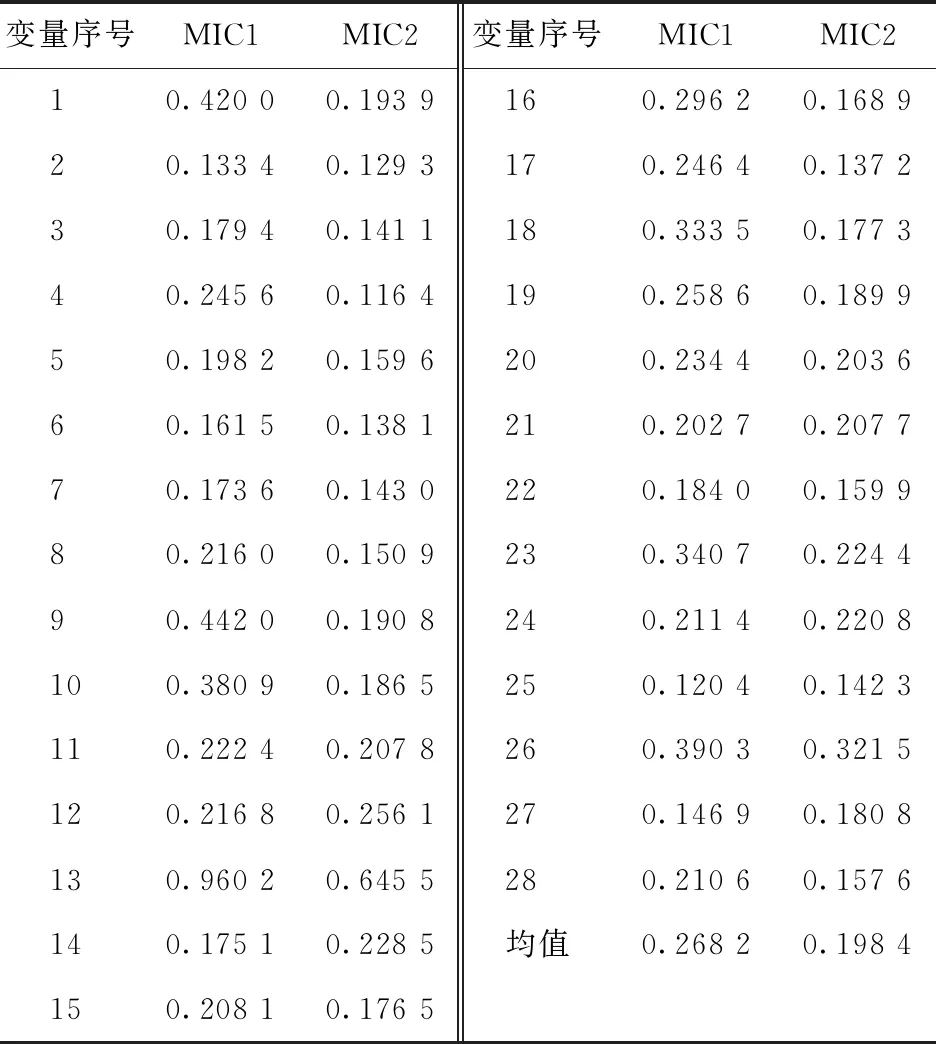
表2 输入变量与目标变量的相关性

为了尽可能地保留关键变量,以所有MIC计算结果的平均值作为分界线对变量进行取舍。由表2可知,输入变量与输出变量1、2的相关性均值分别为0.238 2和0.198 4,而对两个输出变量的平均均值为0.233 3。因此,舍去相关性小于0.233 3的15个输入变量[15,19],保留高于平均均值的13个变量,进行变量间相关性计算。

1.3.2输入变量间相关性分析

同样,采用MIC方法对上述13个输入变量进行相关性分析,结果见图1。

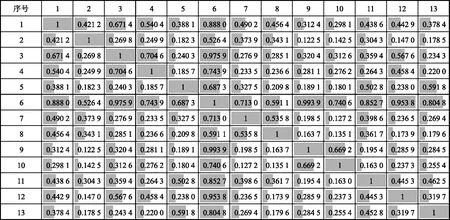
图1 输入变量间相关性分析结果

由图1可知,变量6(装置产氢流量)与多个变量间相关性系数较大(≥0.8),说明其相关性较高,故舍去变量6[20-21]。最终,共保留12个输入变量用于建模,见表3。

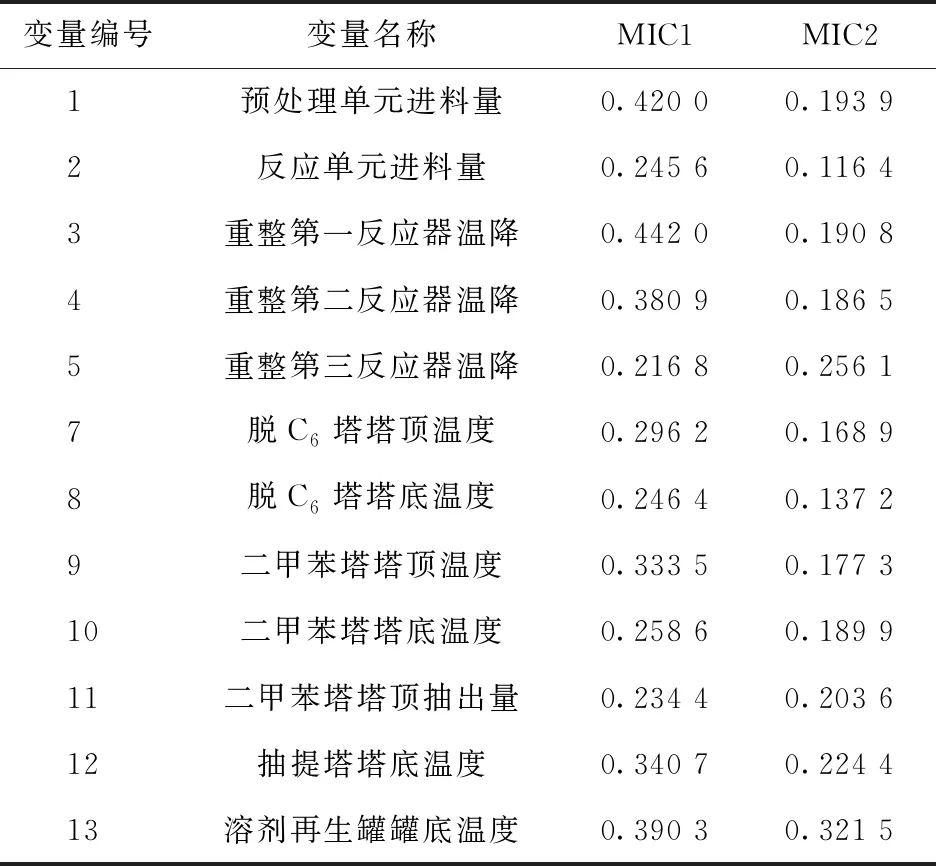
表3 相关性分析后优选的输入变量

2 模型构建与计算结果

BP神经网络具有很强的非线性拟合能力,对具有复杂运行状况和数据强非线性特点的连续催化重整装置建模尤为适用[22]。采用性能优异的B-R训练算法[23],将上述预处理好的数据样本按照70%,15%,15%的比例随机划分为训练集、验证集、测试集3组,训练集和验证集数据样本用于模型参数的训练,测试集数据样本用于验证模型的泛化能力。

2.1 模型结构的确定

2.1.1隐含层数的确定

在隐含层数分别为1～5、每层神经元数分别设置为6,8,10的情况下[23],选择回归系数R和均方根误差RMSE作为评价指标,回归系数R越大,说明模型的预测值越接近真实值,表示模型越精确;均方根误差RMSE越小,表明计算值与真实值误差越小,采用多次计算、对结果求平均值的方法评价不同模型结构对神经网络模型预测精度的影响,结果如图2所示。

由图2(a)可知:对于目标变量苯产品中非芳烃组分含量,当隐含层神经元数为6、隐含层数为3时,获得最大的R和最小的RMSE;当隐含层神经元数为8或10、隐含层数为3时,获得较大的R和较小的RMSE(效果仅次于隐含层数为4时)。由图2(b)可知:当隐含层数为3,隐含层神经元数分别取6,8,10时,均获得最大的R和最小的RMSE。综合考虑隐含层数对两个目标变量的影响,神经网络模型隐含层数选择3为宜。

2.1.2神经元数的确定

依次使用公式经验法和反复试验法来确定模型隐含层的神经元数和最佳神经网络结构[24]。隐含层神经元数由式(3)计算。

(3)

式中:Nhid为隐含层神经元数;Nin为输入层神经元数;Nout为输出层神经元数。

输入变量数为12、输出目标变量数为2,由式(3)可初步确定Nhid=6。在此基础上,将每层神经元数范围扩展为4～8个,探讨神经元数不同对模拟结果的影响。在优化隐含层数为3条件下计算共获得125种组合结构模型的模拟结果,每种组合计算200次,其均值如表4所示。由表4可知,3层隐含层的神经元数分别为8,6,8时(第115组计算结果),模型回归效果最好。最终,优化得到的BP网络模型结构为(12,8×6×8,2)。

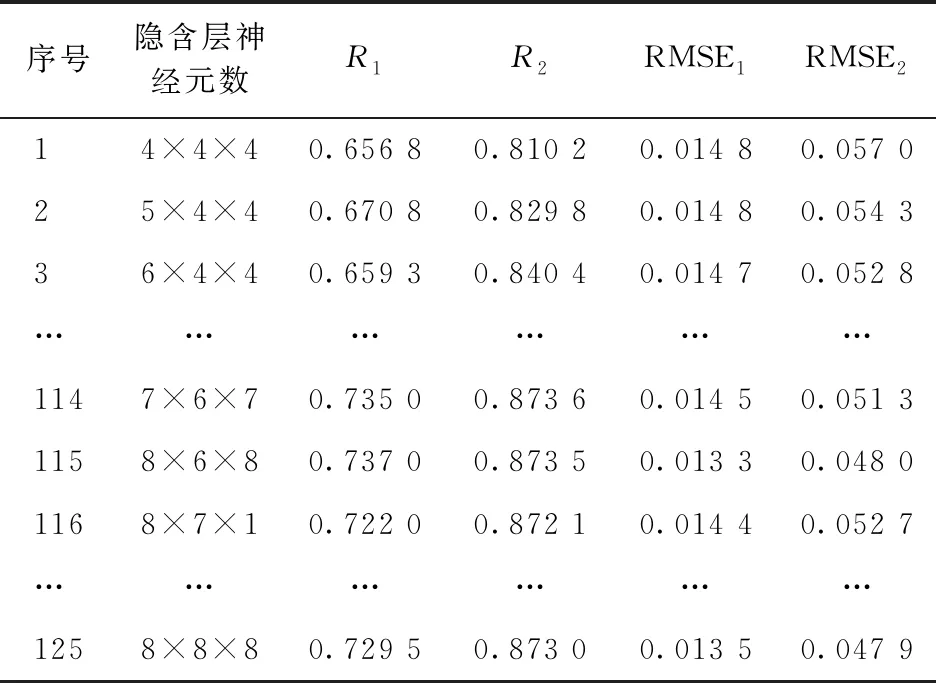
表4 不同神经元组合计算结果

2.2 计算结果分析

基于上述优化的BP网络模型结构进行训练,由测试集数据样本得到模型性能结果,见表5。由表5可知:①对于产品苯中非芳烃含量与甲苯含量,模型预测结果的回归系数分别为0.872 1和0.901 2,说明模型预测值与真实值一致性较好,该模型能够很好地预测装置运行的波动性;②二者的均方根误差分别为0.012 4和0.046 3,表明预测值与真实值偏差较小;③二者平均相对误差(MRE)分别为1.036%和3.312%,表明所建模型预测结果的准确性良好,能够满足化工装置控制精度要求。

图3为采集数据装置运行的真实值与所建神经网络模型预测值的对比结果。由图3可以看出,随着装置运行时间的增加,预测模拟值与装置真实值的变化趋势相同且吻合良好,表明所建模型的预测结果具有较高的准确性,达到了利用该模型预测装置产品中非芳烃含量和甲苯含量的目的,可以用于后续优化工作。

图3 苯产品中非芳烃和甲苯含量模拟值与真实值变化趋势对比

3 装置操作参数优化

结合现场装置参数调节难度和操作参数对产品质量(苯产品中非芳烃和甲苯含量)影响程度的大小,选取易于调控、对产品质量影响程度较大的5个参数进行优化分析,并确定参数优化合理区间,见表6。除待优化输入变量外,其他输入变量采用2.1节预处理后变量数据的平均值。

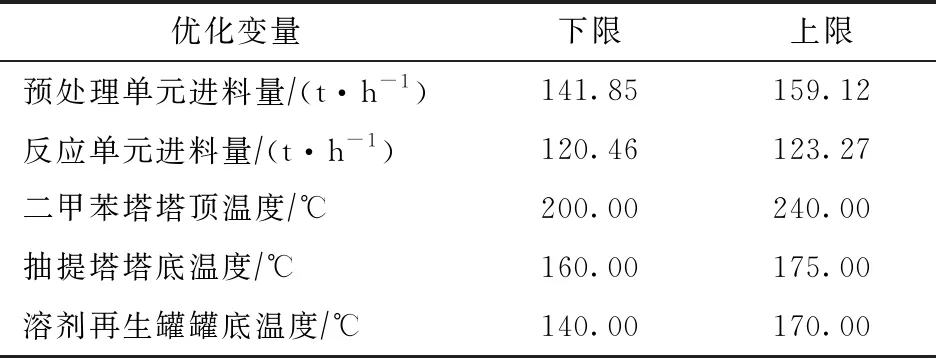
表6 优化参数及其变化范围

采用带精英策略的遗传算法NSGA-Ⅱ对上述变量参数进行优化求解,求解器参数设置:最优个体系数为0.3,种群规模为200,最大进化代数为500,停止代数为200,适应度函数偏差为1×10-4,其他参数设置为函数默认值。输入变量参数的变化范围介于变量变化下限与上限之间,优化目标为苯产品中非芳烃质量分数(y1)和/或甲苯质量分数(y2)最小。变量优化结果见图4,图中点N代表催化重整装置正常操作点,点A、点B、点C分别为优化后的操作点。优化后的输入变量和目标函数如表7所示。

图4 多目标优化最优解集

表7 最优解优化变量及目标函数

由图4可以看出,对催化重整装置苯产品质量优化的方案有3种:①为最大程度降低产品中非芳烃含量,则选择操作点A工况,此时产品中非芳烃质量分数降低40.12%,但甲苯含量有所增加;②为保持甲苯含量不增加的同时降低非芳烃含量,则选择操作点B工况,此时产品中非芳烃质量分数降低36.85%;③为同时降低苯产品中非芳烃和甲苯的含量,则选择最佳操作点C工况,此时苯产品中非芳烃和甲苯的质量分数分别降低24.38%和82.58%。从以上分析可知,可通过改变相关操作参数实现提高苯产品质量的目的,方案③对应的操作点C工况对提高苯产品质量的效果最佳。

4 结 论

(1)基于催化重整装置的实时数据,建立了实时数据处理规则,将采集到的60个变量简化至14个,在保证数据完整性和准确性的同时,降低了数据的维度,为后续建模提供了简约的数据集。

(2)基于处理后的数据集,建立了苯产品质量的预测模型,当模型输入变量为12个,输出变量为2个,隐含层为3层,3层隐含层的神经元数分别为8,6,8时模型的预测结果最优,因此优化的模型结构为(12,8×6×8,2)。

(3)经过模型训练和验证,对于苯产品中的非芳烃含量与甲苯含量,模型预测结果的回归系数(R)分别为0.872 1和0.901 2;二者的均方根误差分别为0.012 4和0.046 3,平均相对误差(MRE)分别为1.036%和3.312%,表明所建模型预测值与真实值一致性较好,预测精度较高。

(4)采用带精英策略的遗传算法NSGA-Ⅱ对影响产品质量较大的5个操作变量进行优化,优化后的工况下,苯产品中非芳烃和甲苯质量分数分别可降低24.38%和82.58%,说明所建模型可用于装置的产品质量预测和调控,有利于现代工厂智能化建设。