Saturated absorption spectrum of cesium micrometric-thin cell with suppressed crossover spectral lines
Junlong Han(韩俊龙), Bowen Wang(王博闻), Junhe Zheng(郑俊鹤), Shuyuan Chen(陈书源),Wei Xiao(肖伟), Teng Wu(吴腾),2, Hong Guo(郭弘),2, and Xiang Peng(彭翔),2,†
1School of Electronics,Peking University,Beijing 100871,China
2Center for Quantum Information Technology,Peking University,Beijing 100871,China
Keywords: micrometric-thin cells,saturated absorption spectrum,hyperfine Zeeman splitting,crossover spectral lines,laser frequency stabilization
1.Introduction
Ultra-thin alkali-vapor cells (UTCs) are specially constructed atomic cells in which the alkali atoms are sealed between two glass plates with a well-polished thin chamber etched on inner walls.UTCs in thickness range of 20–3000 nm are often referred to as nanometric-thin cells,while those in range of 20–900 µm are often referred to as micrometric-thin cells.[1]Because of their distinct structure,UTCs can exhibit numerous novel physical properties and are used to explore Dicke narrowing effect,[2]atom-surface van der Waals interaction,[3]Lamb shift,[4]hyperfine Paschen-Back regime,[5]the suppression of crossover lines in saturated absorption spectrum,[6]coherent excitation of Rydberg atoms,[7]limits of distribution of atomic velocities,[8]lightinduced atomic desorption,[9]and spectroscopy of hot alkali dimer vapor,[10]and have remarkably high potential value in fields like superluminal propagation,[11]compact atomic clocks,[12]strong magnetic field sensing,[13]atomic narrowband filtering,[14]atomic pressure gauges,[15]micromechanical resonator systems,[16]RF electric field sensing,[17]and laser frequency stabilization.[18]Although MCs can hardly exhibit pronounced Dicke narrowing and surface potential effects like nanocells, MCs are easier to fabricate, require lower heating temperature,and possess greater absorption under the same experimental conditions,which omits the acquisition of first and second derivative spectra commonly used in nanocells.[19]Additionally, compared with conventional atomic cells, MCs can suppress the crossover lines in saturated absorption spectra and leave non-crossover lines clearly revealed, which have indispensable potential in research of atomic spectral splitting and wide-range atomic magnetometers for measuring strong magnetic fields.
To obtain a clearly discrete splitting of atomic transitions in strong magnetic field,sub-Doppler-width atomic spectra are necessary.This is because the Doppler broadening of alkali atoms at room temperature is typically in range of 400–1000 MHz,[1]which exceeds the separation of adjacent Zeeman sub-levels under strong magnetic field near the hundred-G scale.MCs can realize sub-Doppler-width atomic spectra by saturated absorption spectroscopy,[20]fluorescence spectroscopy,[21]narrow-bandwidth EIT resonance,[22]etc.Among them,saturated absorption spectroscopy is easy to operate and convenient for applications.In addition, MCs possess unique properties of suppressing crossover spectral lines in saturated absorption spectrum, which is quite valuable for precision spectrum, since recognizing non-crossover spectral lines submerged between massive crossover spectral lines in strong magnetic field could be quite challenging.[23]Meantime,the ultra-thin chambers of MCs are expected to lower the influence of spatial magnetic-field gradient on spectra,[13,24]which is valuable for high-spatial-resolution mapping of highgradient strong magnetic field.Currently, the split saturated absorption spectra in strong magnetic fields with suppressed crossover spectral lines have been experimentally observed in Rb and K atomic MCs,[1,13,20,25]with valuable applications of wide-range magnetometry proposed.However, few investigations have been made on comprehensive theoretical calculations explaining the mechanism of MCs suppressing crossover spectral lines, with the strength and direction of the magnetic field, the propagation direction and polarization of the pump/probe beam considered.Also, experimental verifications using Cs MCs are indispensable, which is valuable for research of precision spectrum and magnetometry in strong magnetic fields.
In this paper, a self-designed Cs MC with thickness of 100 µm is used, and a clear splitting of saturated absorption spectrum of Cs D1 line with linearly polarized pump and probe beams in a magnetic field near 600 G is obtained experimentally.Thanks to the thin chamber of the MC, the crossover saturated absorption spectral lines that may be abundant in conventional cells are largely suppressed, and non-crossover lines are retained to match well with the transition frequencies between Zeeman sub-levels.Also,the effect of magnetic field gradient in the direction of MC’s thickness(perpendicular to the glass plates)is expected to be reduced.A theoretical model for saturated absorption spectrum of the MC that simultaneously considers the magnetic field direction,the directions of pump/probe beam’s propagation and polarization is established,and a fairly good agreement between calculated results and experimental results is achieved.This model explicitly explains the suppression of crossover lines in MCs, and is promising to be widely used to calculate the splitting of saturated absorption spectrum under diverse pump/probe beam polarization,as well as to analyze the effect of magnetic-field direction.In addition, with suppressed crossover lines, Zeeman sub-levels are clearly revealed, and laser frequency stabilization on transitionFg=3,mg=3↔Fe=4,me=4 is realized, which may pave the way for high spatial resolution and high-sensitivity magnetometry in strong magnetic fields.
2.Experimental setup and theoretical analysis
2.1.Experimental setup
The experimental setup is shown in Fig.1.The UTC used in this paper is a Cs MC without buffer gas, as shown in Fig.1(a), where Cs atoms are contained in the chamber marked by red dashed lines, which is about 100 µm thick,15 mm high and 5 mm wide.The MC is placed in a sealed furnace for heating and the furnace is placed in the center of the permanent magnet ring(PM)which provides the required strong magnetic field, as shown in Fig.1(b).The magnetic field strength at MC is measured to be about 600 G.Note that the magnetic-field strength induced by PM is not spatially uniform, experimental results will inevitably be affected by magnetic field gradient.A laboratory reference framexyzis built in Fig.1(c), where the magnetic field direction is taken as thez-axis.The wavelength of emitted beam from the external cavity diode laser(ECDL,Toptica DL-Pro)is near D1 line of Cs atoms(about 894.6 nm).After passing through the neutral density filter (NDF), half-wave plate (λ/2) and polarization beam splitter(PBS),the incident light is split into a pump beam polarized alongx-axis and a probe beam polarized alongy-axis.The pump beam propagates along the positive direction ofz-axis, and probe beam propagates along the negativezdirection after being reflected by mirrors,and then being incident into the photodetector (PD) after passing through the PBS again.Adjusting the NDF and the half-wave plate, the intensities of the pump and probe beams can be flexibly regulated.In experiments, adjusting an appropriate pump/probe beam intensity and scanning the emission frequency of ECDL,saturated absorption spectrum of the MC can be monitored and measured with the PD.The PD signals can yield error signals via the lock-in amplifiers(LIA),and then fed back to laser controller via a proportional-integral-derivative(PID)to stabilize the laser frequency.
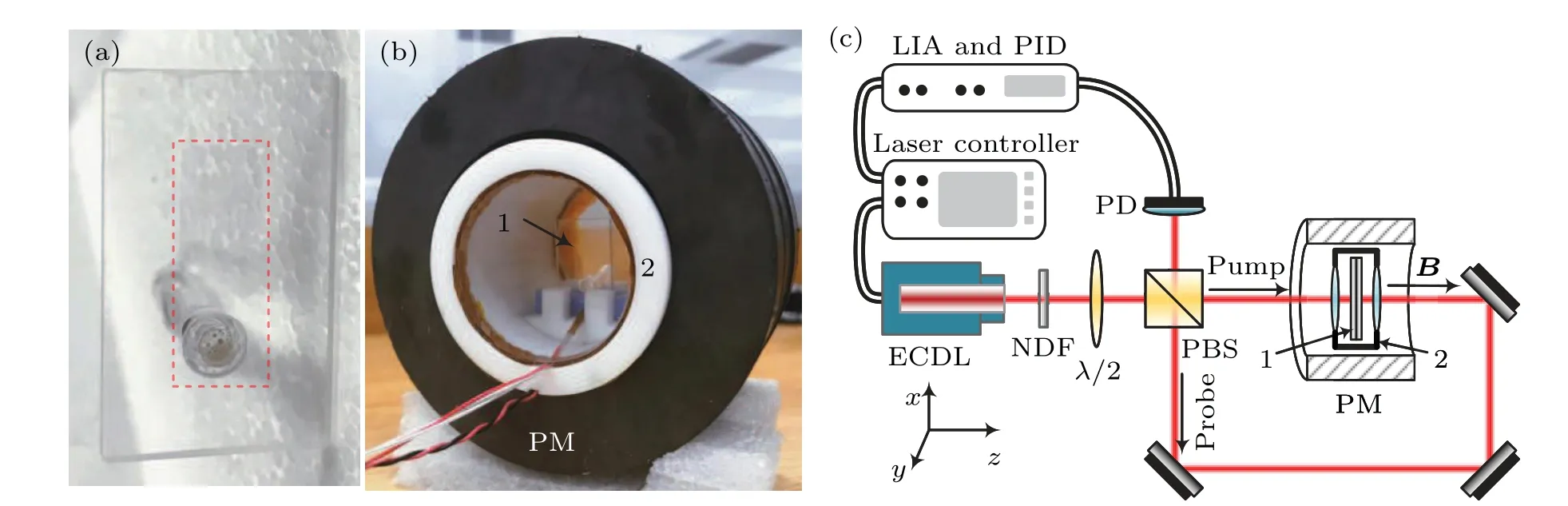
Fig.1.(a)The MC used in experiments,and the red dashed square marks the thin chamber where Cs atoms are sealed.(b)The setup with the MC placed in the heating furnace and the PM:(1)MC,(2)furnace.(c)Schematic diagram of the experimental setup.LIA:lock-in amplifier,PID:proportional-integral-derivative module,PD:photodetector,ECDL:external cavity diode laser,NDF:neutral density filter,λ/2:half-wave plate,PBS:polarization beam splitter,PM:permanent magnet ring.
2.2.Theoretical analysis
To properly explain the saturated absorption spectrum of the MC in strong magnetic fields, effects of the suppressed crossover spectral lines need to be accounted for,as well as the strength and direction of the magnetic field, the propagation direction and polarization of the pump/probe beam.Hereby,a calculation method that explains the mechanism of crossover lines suppressed by the thin structure of MCs is introduced.Taking the direction of magnetic field asz-axis, the linearly polarized pump and probe beams propagate along+zand−zdirections, and are polarized alongxandydirections.Their electric fields can be expressed as
whereE0andE1are the amplitudes of the pump and probe beams,e±1=ex±ieyare the unit vectors in spherical basis,exandeyare the unit vectors ofxandyaxes,k=2π/λrefers to the wave vector along±zdirections, andωrepresents the laser angular frequency.In dipole approximation,the ground and excited states are mutually coupled through the dipole moment ˆD.Using the Wigner–Eckart theorem,[26]the components of dipole moment operator ˆDqfor Cs D1 line can be expressed as
whereFg,e,mg,e, andJg,eare quantum numbers of the corresponding transition levels,q=0,±1 denote the three components of the dipole moment operator in spherical basis, and〈Jg|| ˆD||Je〉is the reduced matrix element of Cs D1 line.The constantscqFg,mg;Fe,mecan be deduced in terms of the Wigner-3jand Wigner-6jcoefficients denoted by the parentheses and curly brackets respectively,andI=7/2 is the nuclear spin of Cs atoms.
As the levels of Cs D1 line undergo Zeeman splitting,the transitions ofFg=3↔Fe=3,4 andFg=4↔Fe=3,4 are illustrated in Figs.2(a) and 2(b).From Eqs.(1) and (2), it is noted that the pump/probe beam is decomposed into a superposition ofσ−andσ+polarized beams,and the selection rules are ∆m=∓1 in dipole approximation, corresponding to the transitions indicated by the blue and yellow arrows in Fig.2,respectively.Hereby, for simplicity, the labels in Fig.2 are employed to specifically refer to each transition between sublevels of Cs D1 line, i.e., transitions 1–13, 1′–13′refer to the transitions in Fig.2(a),and transitions 1′′–15′′,1∗–15∗refer to the transitions in Fig.2(b).Using the Breit–Rabi formula,[27]the splitting of the transition frequencies of Cs D1 line at different strengths of external magnetic field can be obtained,as shown by Fig.3.From Figs.3(a) and 3(b), mutually overlapped splittings of the transition frequencies can be seen at magnetic field strength of about 600 G, which is of particular interest in analyses of the following experimental results,and transitions 7′and 15′′are designated as the origins of frequency detuning,so as to stay in consistence with the experimental results.
In this paper, the saturated absorption spectrum of MCs is calculated based on the rate equations.[28]Since there are excessive magnetic sublevels in Cs D1 line, it is rather inconvenient to calculate the populations of all sub-levels of ground and excited states.Thus, the populations of excited states are omitted, and only the ground-state populations polarized by the pump beam are accounted for.[29]In this case,atoms pumped by the pump beam will not remain in excited states,but immediately fall back to ground states with certain branching ratios through spontaneous decay, etc.Therefore,this method is more applicable for weak pump beams.
To illustrate the suppressed crossover spectral lines in MCs, an additional factor needs to be included in theoretical analysis.In MCs, owing to the thin-cell structure, atoms pumped to excited states by the pump beam with fasterzdirection velocities are more susceptible to collisions with

Fig.2.Hyperfine Zeeman splitting of Cs D1 transitions,where the transitions of Fg=3 ↔Fe=3,4 and Fg=4 ↔Fe=3,4 are outlined in(a)and(b),and labeled by 1–13,1′–13′and 1′′–15′′,1∗–15∗,respectively,with σ−and σ+transitions distinguished by the blue and yellow arrows.

Fig.3.Frequencies of transitions 1–13, 1′–13′ [blue and yellow lines in(a)]and transitions 1′′–15′′,1*–15*[blue and yellow lines in(b)]at different magnetic field strengths,with transitions 7′ and 15′′ in 600-G magnetic field assigned as the origins of frequency detuning(shown by the black dots).
the inner walls of MCs and fall back to ground states,resulting in loss of pumping efficiency.Taking this mechanism into account in saturated absorption spectral lines, since generating non-crossover lines requires pumping of zero-velocity atoms by the pump beam while crossover lines need pumped atoms with certain velocities alongz-direction, clearly, the pumped atoms for crossover lines are more inclined to collide with the inner walls of MCs and have reduced pumping efficiency,leading to the suppression of crossover lines.To describe this phenomenon,an additional pumping efficiency termη(|v|)is included, and the pumping ratePnow can be expressed as[28,30]
where ˆDrepresents the dipole moment whose components are given in Eqs.(3) and (4), and the electric field of the pump beam,Epump, is given in Eq.(1),PFg,mgandQFg,mgare the populations of Zeeman sub-levels in ground and excited states,respectively, since the populations of excited states are omitted,QFe,me=0.Here, ¯his the reduced Planck constant,Γdenotes the relaxation rate of excited states,andvdenotes the component of atomic velocity alongz-direction;η(|v|) satisfies lim|v|→0η(v)=1 and lim|v|→∞η(v)=0, and monotonically decreases, indicating that atoms with fasterz-direction velocities are more likely to collide with the inner walls of MCs, which in turn leads to lower pumping efficiency.Here,ωFg,mg;Fe,merepresents each of the angular frequencies of the transitions between Zeeman sub-levels of ground and excited states in magnetic fields,as shown in Fig.3.
Since the pump beam is approximated to be weak, the atoms pumped to excited states by the pump beam will immediately fall back to ground states through spontaneous decay,etc.,and the branching ratios can be expressed as[26]
where ∑q′,mg′denotes the summation over all terms satisfying the selection rules.Additionally, Zeeman sub-levels of ground states tend to be equally populated, and the resulting termRFg,mgcan be expressed with rateγgas
wherePeqis the equilibrium population of ground-state Zeeman sub-levels.Using Eqs.(5)–(7), the rate equations forPFg,mgcan be derived as
Setting the left-hand side equal to zero, the steady-state solutions for the populations of ground-state Zeeman sub-levels can be obtained,and then the saturated absorption spectrum of the MC can be calculated by[28]
whereEprobeandW(v)are the electric field of the probe beam given in Eq.(2)and the Maxwell Boltzmann velocity distribution alongz-axis,respectively.
3.Results and discussion
Tuning the intensities of the pump and probe beams(with the 1/e diameter of about 10 mm) to about 10 mW/cm2and 500µW/cm2,respectively,at magnetic field strength of about 600 G,the saturated absorption spectra ofFg=3↔Fe=3,4 andFg=4↔Fe=3,4 are experimentally obtained,as shown in Figs.4(a) and 4(b).Since every two transitions indicated by Figs.2 and 3 may generate a crossover line, with numerous and mutually overlapping transition splittings, the non-crossover saturated absorption spectral lines may be submerged between massive crossover lines in common cells,[23]and spectrum analyzing could be rather tricky.However, because massive crossover lines are effectively suppressed in the MC,the retained experimental non-crossover spectral lines are mostly discrete, and match well with a substantial number of the transitions marked in Figs.4(a) and 4(b).Since some of these transitions are too close in frequency, like transitions 10′and 8 in Fig.4(a), their spectral lines are mutually overlapped.As for the other few transitions,such as transitions 6,7,12,and 13,probably because of the broadening effect of the strong pump beam and small amplitudes of these transitions,with hardly revealed spectral lines, these transitions are not shown in the experimental results.Additionally, some experimental spectral lines,like those between transitions 2 and 2′,3 and 3′,4 and 4′,5 and 5′in Fig.4(a)and between transitions 3′′and 4′′in Fig.4(b), do not match with any transition frequencies, which are likely to be the remained crossover lines with amplitudes reduced by the MC.
Theoretically calculated saturated absorption spectra ofFg= 3↔Fe= 3,4 andFg= 4↔Fe= 3,4 are shown in Figs.4(c) and 4(d).Compared with Figs.4(a) and 4(b),it can be seen that calculated results have achieved a fairly good agreement with experimental ones, with crossover lines largely suppressed and the non-crossover spectral lines matching well with a substantial number of the calculated transition frequencies.Regrettably, minor differences can be observed when comparing the amplitudes and widths of certain spectral lines.Firstly,the spectral lines of transitions 12 and 13 in Fig.4(c)and transitions 1∗, 12∗, 13∗, 14∗, 1′′, 8′′in Fig.4(d)are hardly revealed in experimental results, and the experimental spectral line of transition 1′in Fig.4(a) is not shown in Fig.4(c).Secondly, some spectral lines, like the spectral line of transition 7 in Fig.4(c),are obviously different in amplitude from the experimental results.Thirdly, the calculated spectral lines are commonly narrower in widths.Four reasons are possibly responsible for these differences.Firstly,the theoretical calculation ignores the populations of excited states and treats the pump beam as a weak beam, which directly affects the results of the rate equations, the amplitudes and widths of the calculated spectral lines.Secondly, broadening effect of the strong pump beam is not included in calculations,which may be responsible for the mismatched widths.Thirdly, a uniform and strong magnetic field is not easy to achieve experimentally.Since the cesium atoms in the MC are constrained within an ultra-narrow space alongz-axis(the direction of MC’s thickness), the difference ofz-axis magnetic field imposed on the atoms tends to be negligible, and the effect ofz-axis magnetic-field gradient is expected to be reduced.However,because the atoms are less constrained alongxandydirections in the MC, the gradient along these directions may slightly exert on the saturated absorption spectrum,possibly causing the broadening of the spectral lines.Fourthly,the Zeeman sub-levels could be coupled by the strong magnetic field,[31]leading to additional modifications of transition probabilities,[32]which could also be responsible for the partially mismatched amplitudes in theoretical results.Although these possible factors lead to limited accuracy of the calculated results, massively suppressed crossover lines are remarkably shown, and the non-crossover lines match well with quite a few transition frequencies.In addition,this calculation method also accounts for the magnetic field direction,the pump/probe beam’s propagation direction and polarization,which is valuable for research on the splitting of atomic levels in strong magnetic fields and related applications of MC-based strongfield magnetometers.
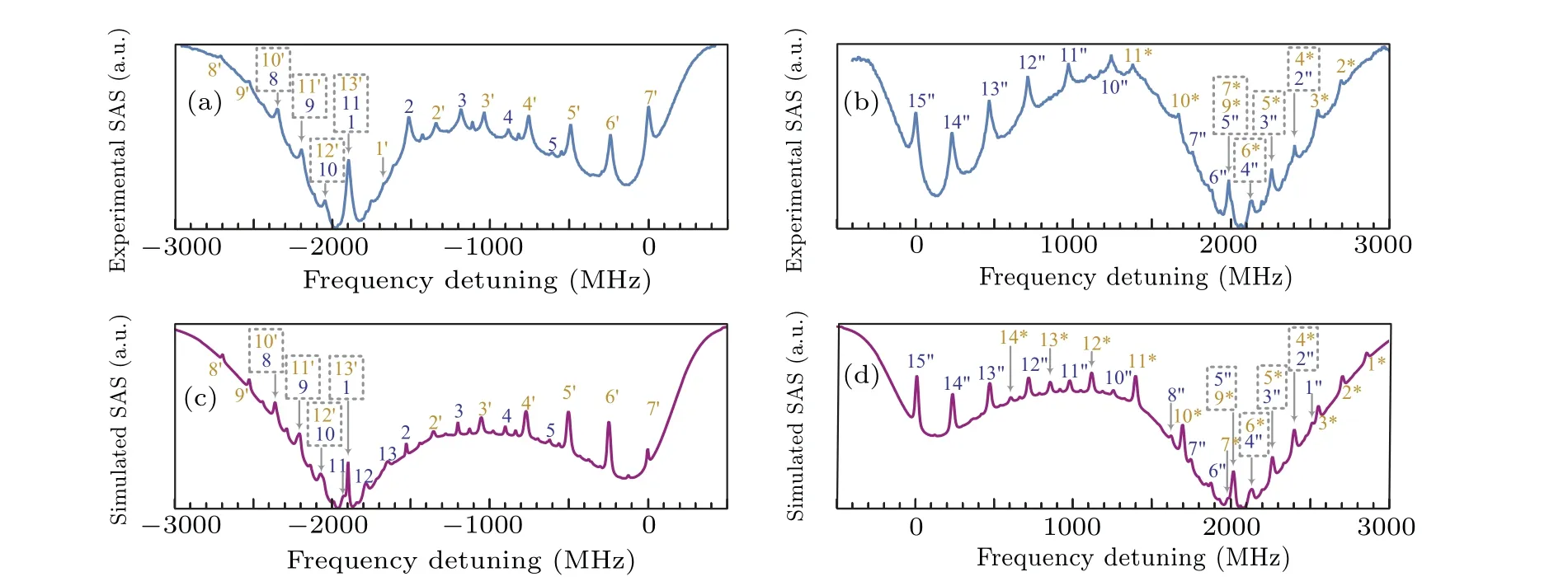
Fig.4.[(a),(b)]Experimental saturated absorption spectra(SAS)of Fg=3 ↔Fe=3,4 and Fg=4 ↔Fe=3,4 using the MC at magnetic-field strength of about 600 G,with the transitions marked on corresponding spectral lines.The dashed squares indicate the transitions that are very close in frequency with mutually overlapped spectral lines.[(c),(d)]Theoretically calculated saturated absorption spectra of Fg=3 ↔Fe=3,4 and Fg=4 ↔Fe=3,4 at the same magnetic-field strength,with transitions marked.

Fig.5.(a)Frequency deviation of ECDL for 1200 s in both frequencystabilized state(red line)and free-running state(blue line),where transition 7′ is used as the frequency reference.(b)Modified Allan deviation obtained from ECDL in both frequency-stabilized state(red dotted line)and free-running state(blue dotted line)at different averaging times.
Furthermore, with the above saturated absorption spectral lines in the MC, the laser frequency stabilization of the ECDL (about 300-kHz typical linewidth) is implemented using transition 7′at 600-G magnetic field strength, and the results are shown in Fig.5.Figure 5(a)presents the frequency deviation of the ECDL in frequency-stabilized (red line) and free-running states (blue line), with the frequency deviation stabilized from about 45 MHz for 1200 s in free-running state.Figure 5(b) illustrates the calculated modified Allan deviation in frequency-stabilized (red dotted line) and freerunning states(blue dotted line),where the Allan deviation of frequency-stabilized state decreases with increasing averaging time, with the stabilization lowering to about 9.87×10−12at an averaging time of about 165 s,while the Allan deviation of free-running state decreases and then increases with increasing averaging time.Also, a lower Allan deviation has been achieved at each averaging time in frequency-stabilized state.The frequency stabilization using the MC could be promising for wide-range high-sensitivity magnetometry by extracting the frequency shift of Zeeman transitions from zero magnetic field in two possible ways, apart from scanning and detecting the experimental spectra lines.[13]First, the ECDL with frequency stabilized to transition 7′could be combined with a high-frequency electro-optic modulator, and the generated sidebands may be employed to track the frequency of zerofield Zeeman transitions using a reference Cs cell, similarly to Ref.[33].Second, the beat frequency of the frequencystabilized ECDL and another laser with frequency stabilized to zero-field Zeeman transitions could also reflect the magneticfield strength.With the suppressed crossover lines and ultrathin thickness of the MC, the two methods are promising for strong-field magnetometry with high spatial resolution and high sensitivity.
4.Conclusions
In summary,a self-designed Cs atomic MC with a thickness of 100µm is prepared,and its saturated absorption spectra of Cs D1 line at magnetic field strength of 600 G is experimentally performed,in which the pump and probe beams are mutually perpendicular linearly polarized beams,and the magnetic field is parallel to the propagation direction of the pump beam.Due to the unique thin structure and small volume of the MC, a substantial number of crossover spectral lines are effectively suppressed, and the effect of magnetic field gradient along the direction of MC’s thickness is expected to be reduced.Consequently, Zeeman splitting of the hyperfine structure in strong magnetic field is clearly shown.A calculation method for saturated absorption spectrum in MCs accounting for the magnetic field direction,pump/probe beam’s propagation direction and polarization is proposed to achieve fairly good agreements between theoretical calculations and experimental results, its possible limitations and further improvements are also analyzed.This convenient method successfully explains the mechanism of the suppressed crossover lines in MCs and is promising for analyzing the effects of magnetic field direction, polarizations and propagation directions of beams on the present MC-based wide-range magnetometers.In addition,a discrete transition of Zeeman sub-levels is used to stabilize the laser, which may allow new possible approaches for high spatial resolution and high-sensitivity magnetometry of strong magnetic fields.
Appendix A:Explicit descriptions of the calculations
For a more specific description of the calculation method adopted,some intermediate results in calculations are partially presented here.Taking the transitions ofFg=3↔Fe=3,4 as an example, the pumping rates in MCs can be derived by substituting Eqs.(1), (3), and(4)into Eq.(5), and the results are given as follows:
where∆Fg,mg;Fe,me=1+[(ω −ωFg,mg;Fe,me)+kv]2.Substituting Eqs.(3) and (4) into Eq.(6), the results of branching ratios from excited statesFe=3,4 to the ground stateFg=3 are given by as follows:
Since a normalization is performed in Eq.(6) on the relaxation intensities from each Zeeman sub-level of excited states to ground-state sub-levels,the sum of all elements in each row of Eqs.(A3)and(A4)is equal to 1.
With the results in Eqs.(A1)–(A4), the rate equations can be conveniently formulated according to Eq.(8).Because of the numerous transitions between Zeeman sub-levels,each rate equation may contain excessive terms.Thus,only the rate equation ofP3,−3is given as follows:
and other equations,i.e.,the rate equations forP3,−2–P3,3can be obtained similarly.
To obtain simulated saturated absorption spectrum,Eq.(9)should be calculated for different frequency detunings,and an integral over all velocity groups is needed.Since analytical solutions of the rate equations could be rather complicated,the population is solved numerically for different velocities,and substituted into Eq.(9)to perform the numerical integral.
Acknowledgement
Project supported by the National Natural Science Foundation of China(Grant Nos.61571018 and 61531003).
- Chinese Physics B的其它文章
- First-principles calculations of high pressure and temperature properties of Fe7C3
- Monte Carlo calculation of the exposure of Chinese female astronauts to earth’s trapped radiation on board the Chinese Space Station
- Optimization of communication topology for persistent formation in case of communication faults
- Energy conversion materials for the space solar power station
- Stability of connected and automated vehicles platoon considering communications failures
- Lightweight and highly robust memristor-based hybrid neural networks for electroencephalogram signal processing

