培森柳江特大桥主梁索导管角度修正研究

刘志航

(广西新发展交通集团有限公司,广西 南宁 530007)

0 引言

预应力混凝土部分斜拉桥介于预应力混凝土梁桥与常规斜拉桥之间,在结构上以混凝土梁受力为主,斜拉索受力为辅,但斜拉索对主梁的受力状态和线形控制至关重要。斜拉索一端通过索导管锚固在主梁上,索导管是具有一定长度的钢管,索导管的安装角度出现偏差就会导致斜拉索在索导管中无法居中,甚至触碰到索导管壁,导致斜拉索不能将索力完全传递到主梁上,产生附加力,对主梁受力状态造成不利影响。本文以培森柳江特大桥主梁索导管为研究对象,考虑斜拉索垂度、主梁预拱度以及索塔压缩变形三个因素对索导管倾角的影响,解决工程上常见的索导管和斜拉索中心偏差较大的问题。

1 工程概况

培森柳江特大桥主桥采用(145+280+145)m双塔单索面预应力混凝土部分斜拉桥,全长570 m,边中跨比为0.518 m,桥面宽29 m,全桥共70个悬臂浇筑段和2个边跨合龙段,1个中跨合龙段。其中11～33号悬臂节段为有索区,全桥共46对斜拉索,斜拉索锚端布置在箱梁横断面的顶板中央区域,每个锚固点横向两组,中跨无索区长度为20 m,斜拉索在索塔上锚固点距离为1 m,在主梁上锚固点距离为4 m,如图1所示。

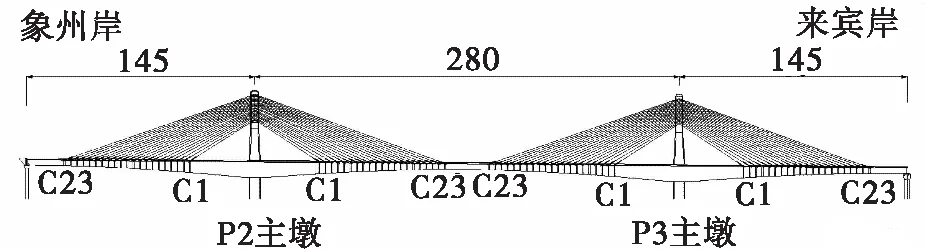
图1 培森柳江特大桥主桥结构形式图(m)

2 考虑斜拉索垂度影响的索导管角度修正

斜拉索在设计时是以直线的形式锚固于主梁和索塔间,而实际情况斜拉索在自重的作用下会出现下挠[1],因此锚固于主梁端的索导管在安装定位时,不能够按照设计斜拉索所在直线确定的角度进行控制,需要将斜拉索作为一条悬索曲线进行研究,对索导管的安装角度进行修正[2]。郑丽凤等[3]对比分析了几种悬索理论计算方法的差异,得出悬链线法和堀氏法较加氏法精度更高。李伟等[4]使用堀氏法对铜陵公铁两用长江大桥斜拉索两锚固端进行角度修正,使斜拉索与索导管中心偏差控制在2 cm以内。

为求得索导管的修正角度,本文采用悬索垂度理论说明和推导如下[5]。

如下页图2所示,弧线AB为在自重及张力作用下的斜拉索;A、B为两锚固点;TA为A点张力;TB为B点张力;H为张力在水平方向上的分力;VA和VB为张力在AB两点竖直方向的分力;l为斜拉索在水平方向上的投影长度;h为斜拉索在竖直方向上投影的长度;L为斜拉索实际长度。C点处的切线水平,悬索曲线的特征参数为m;CA段弧长为SA;CB段弧长为SB。

图2 悬索垂度理论计算索导管倾角示意图

根据力的平衡原理可知水平分力H是一个与位置无关的定值,设P为斜拉索单位长度自重,令:

m=H/P

(1)

Z=L/2m

(2)

则斜拉索长:

(3)

(4)

CA段曲线长:

(5)

A点处曲线的切线斜率:

(6)

则在斜拉索自重作用下梁端索导管修正后的角度:

α=tan-1KA

(7)

此方法被称为索长逐次接近法,应用原理是将设计索长L作为初始值,用式(3)和式(4)进行迭代,使L逐渐逼近实际状态,其判断依据是前后两次迭代计算的Z的差值趋于0。

3 考虑主梁预拱度及索塔变形对索导管角度的影响

根据以往工程经验,对于预应力混凝土斜拉桥,仅考虑斜拉索自重进行主梁索导管角度修正会导致索导管与桥面夹角普遍偏大,导致斜拉索处于索导管的下半部分,甚至接触到索导管的下边缘,斜拉索自重对索导管角度的修正程度不够。

3.1 主梁预拱度对索导管角度的影响

考虑成桥十年时的主梁混凝土徐变和正常通行时桥面活载的影响,索导管的标高会随着主梁的下挠而降低,因此需要设置预拱度来抵消索导管标高的下降,保证索导管的位置和角度和设计相符[6-7]。

如图3所示,A点为索塔上某一根斜拉索锚固点;B0为斜拉索梁端设计锚固点;B1为斜拉索梁端实际锚固点;AB0为设计斜拉索位置;L0为拉索设计长度;AB1为主梁设置预拱度后斜拉索的实际位置;L1为拉索实际长度;OA为斜拉索在索塔上的投影高度;OB0为斜拉索在主梁上的投影长度;O为斜拉索塔端锚固点在主梁上的投影点;Δh1为主梁预拱度值;θ1为设置预拱度后斜拉索的倾角变化量。则设计索长:

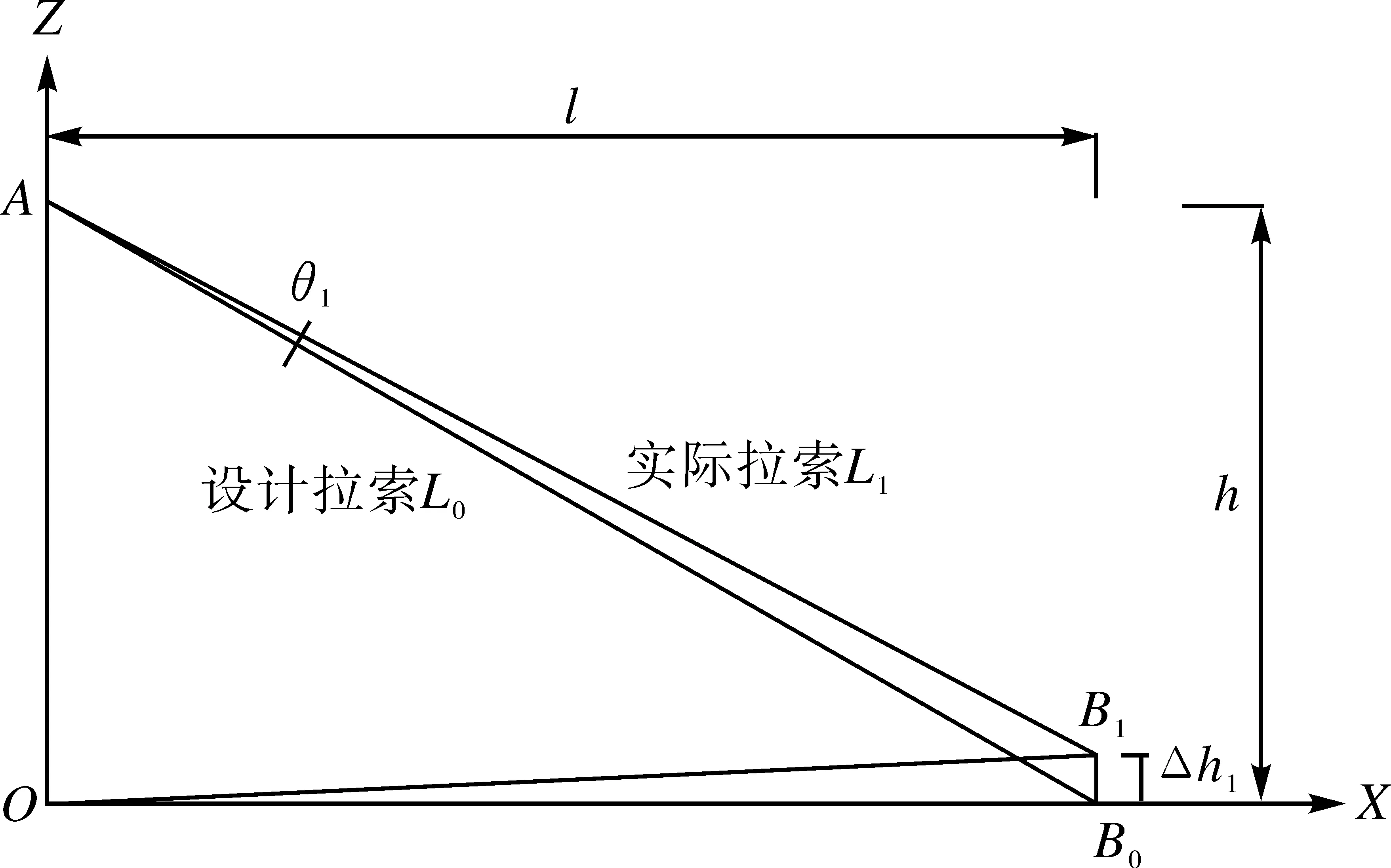
图3 主梁预拱度作用下的索导管角度修正示意图

(8)

实际索长:

(9)

根据余弦定理可得索塔压缩修正角度为:

(10)

3.2 索塔变形对索导管角度的影响

索塔在斜拉索竖向分力的作用下受压,混凝土将发生压缩变形,从而造成斜拉索塔端锚固点实际高程比设计高程低,斜拉索与水平方向的倾角将变小,因此要考虑索塔压缩变形对索导管角度的影响。

如图4所示,B点为主梁上某一根斜拉索的梁上锚固点;A0为斜拉索塔端设计锚固点;A1为斜拉索塔端实际锚固点;A0B为设计斜拉索位置;L0为拉索设计长度;A1B为索塔受到压缩后斜拉索的实际位置;L1为拉索实际长度;OB为斜拉索在主梁上的投影长度;OA0和OA1为斜拉索在主塔上的投影高度;O为斜拉索塔端锚固点在主梁上的投影点;Δh2为索塔压缩量,斜拉索是在索塔浇筑完成后达到规定龄期后开始穿束和张拉;θ2为塔压缩后斜拉索的倾角变化量。

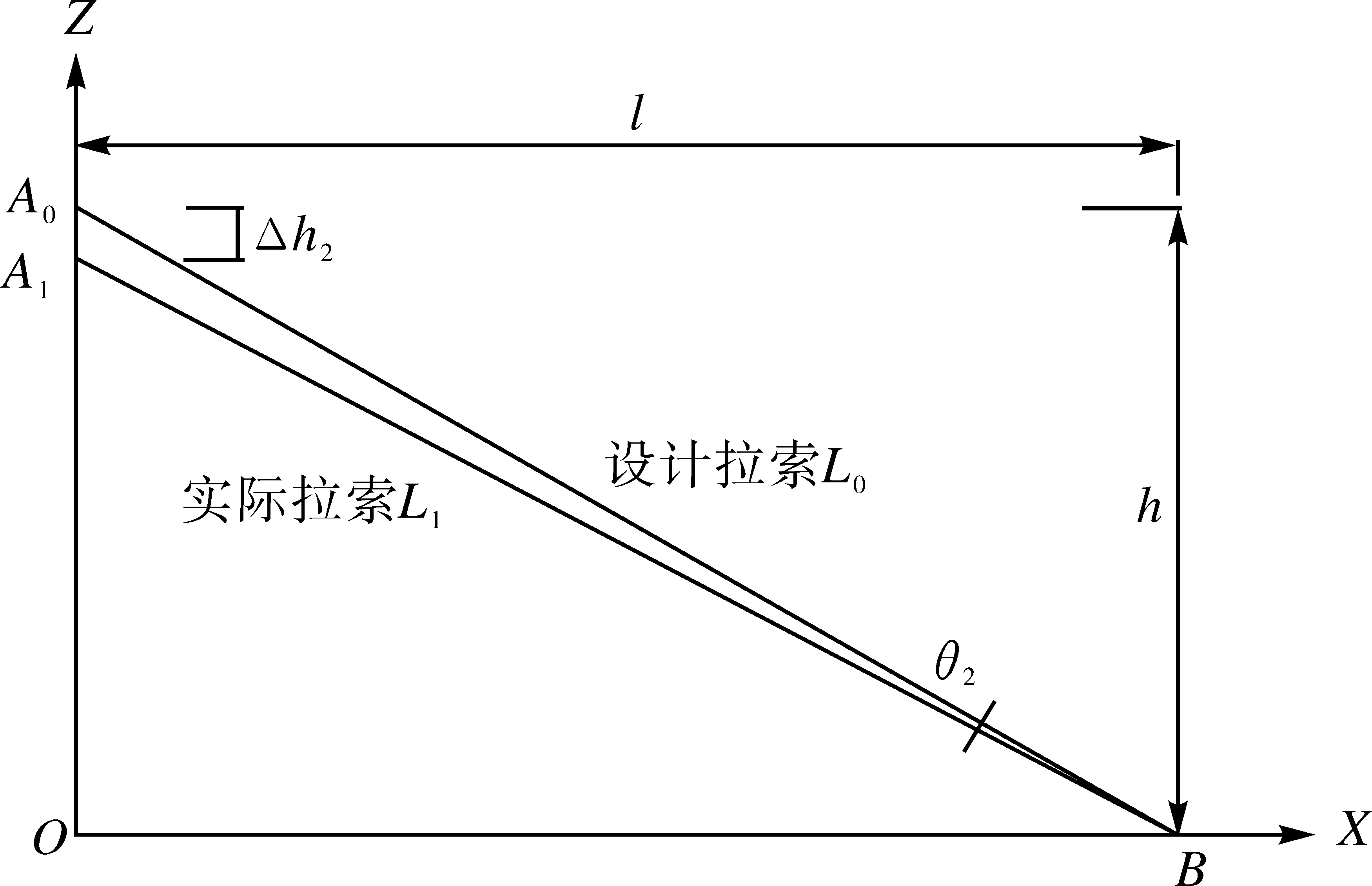
图4 索塔压缩变形作用下的索导管角度修正示意图

则设计索长:

(11)

实际索长:

(12)

根据余弦定理可得索塔压缩修正角度为:

(13)

4 工程应用

培森柳江特大桥主桥斜拉索规格为55φ15.2 mm单丝涂层环氧喷涂钢绞线,标准强度为1 860 MPa。全桥共计4×23根斜拉索,钢绞线采用环氧喷涂工艺,斜拉索外层采用HDPE护套,斜拉索与外层HDPE护套管单位合成重量P为0.74 kN/m,单根斜拉索通长设置,通过塔上的转向索鞍,锚固于边中跨主梁上。主梁11～33号悬臂节段为有索区,按照设计文件斜拉索编号依次为C1、C2、C3……C22、C23。因篇幅有限,选取象州岸边跨C1、C5、C9、C13、C17、C21、C23为研究对象。

4.1 斜拉索垂度影响的索导管角度修正计算

对象州岸边跨C1、C5、C9、C13、C17、C21、C23七束斜拉索进行迭代计算,结果见表1。

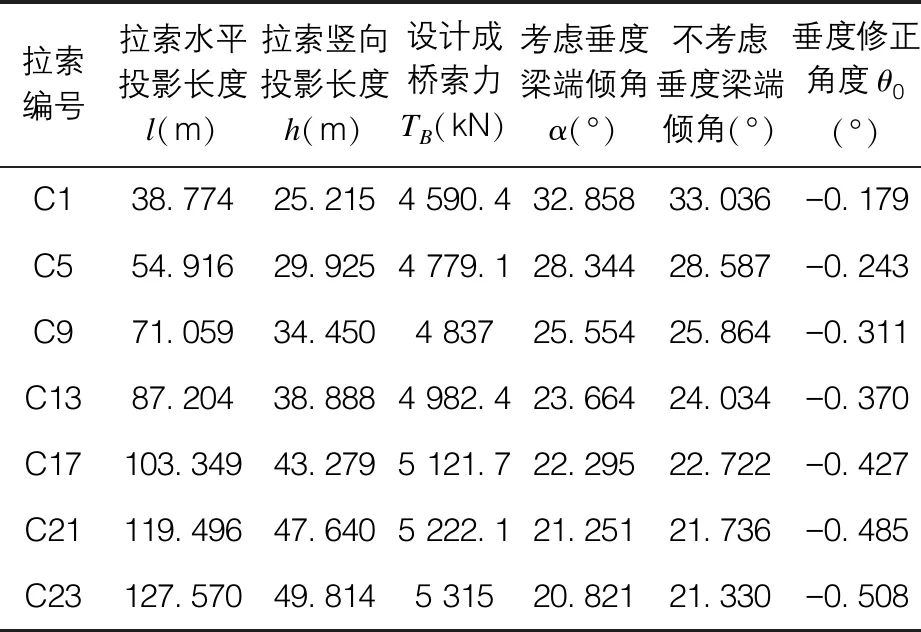
表1 考虑斜拉索垂度影响的索导管倾角计算结果表

由表1可知,在垂度作用下,斜拉索梁端倾角均比不考虑垂度时的倾角小,这一计算结果与实际情况相符;从C1到C23,随着斜拉索倾角的减小,垂度修整角度θ0的绝对值增大,垂度影响的作用变大,这是因为斜拉索的倾角越小,斜拉索越接近水平状态,且斜拉索在水平方向的投影长度也在增加,自重产生的弯矩随之增加。

4.2 主梁预拱度影响的索导管角度修正计算

根据式(8)～(10)以及图3计算索主梁预拱度对索导管角度修正结果见表2。

表2 考虑主梁预拱度影响的索导管倾角修正计算结果表

4.3 索塔变形影响的索导管角度修正计算

根据以往工程经验和有限元计算综合考虑,索塔压缩量Δh2取3 cm。根据式(11)～(13)以及图4计算索塔压缩变形对索导管角度的修正结果见表3。

表3 考虑索塔压缩变形影响的索导管倾角修正计算结果表

4.4 索导管倾角综合修正

前文分别计算得到了在垂度、主梁预拱度以及索塔压缩变形作用下对索导管倾角的修正值,考虑上述三种影响因素综合作用下索导管的角度修正值为:

θ合=θ0+θ1+θ2

(14)

索导管安装角度:

α安装=α设计+θ合

(15)

根据式(14)～(15)计算索导管安装角度见表4,影响索导管安装角度的各因素权重见表5。

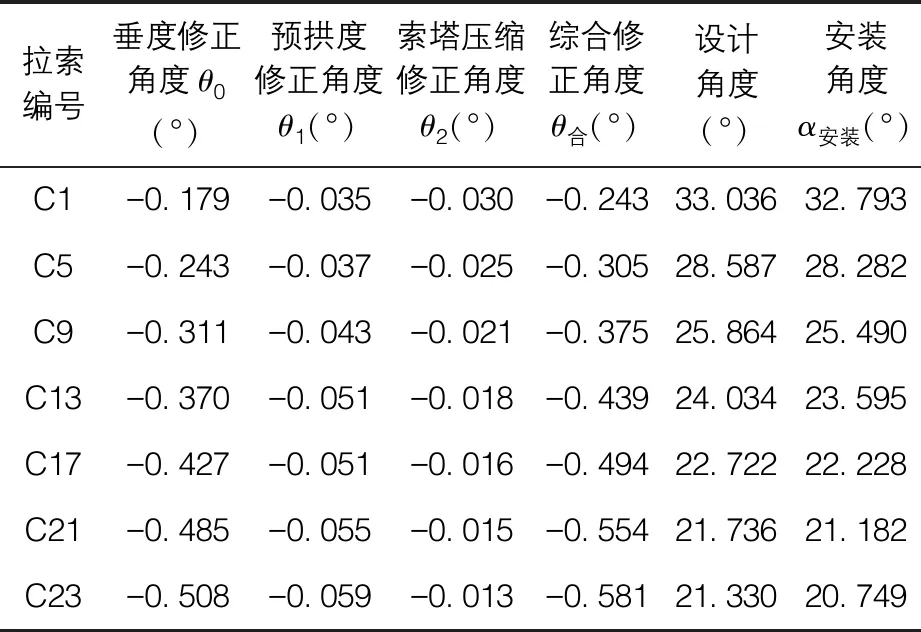
表4 索导管倾角综合修正计算结果表

表5 索导管倾角修正因素权重表

从表4知,编号为C1的斜拉索修正角度最小为-0.243 °,编号为C23的斜拉索修正角度最大为-0.581 °,且综合修正角度θ合的绝对值随着设计倾角的变小而增大。

对培森柳江特大桥主桥象州岸边跨23对斜拉索张拉后与索导管的相对位置进行检测,中心偏差均在1 cm以内。从表5可以看出斜拉索垂度对索导管倾角的影响大于主梁预拱度对索导管倾角的影响,主梁预拱度对索导管倾角的影响大于索塔压缩变形对索导管倾角的影响;索塔压缩变形作为索导管角度修正的次要因素,其影响程度从C1到C23逐渐减弱,对C1斜拉索影响最大,占总修正值的12%,索塔压缩变形对索导管倾角的影响不可忽视。

5 结语

本文通过工程实例,综合考虑了斜拉索垂度、主梁预拱度以及索塔压缩变形三个因素对索导管倾角的影响,用悬索垂度理论计算得到了斜拉索垂度对索导管倾角的修正值,用余弦定理计算得到了主梁预拱度和索塔压缩变形对索导管倾角的修正值,对索导管安装角度进行综合修正,用于指导现场索导管安装,使培森柳江特大桥的斜拉索完全处于索导管的中心。由于本项目主梁跨度较大,梁段混凝土在浇筑完成至全桥合龙周期较长,主梁混凝土发生收缩引起索导管定位坐标发生变化未考虑在内,这也是影响索导管倾角的因素。随着工程参数的不断积累,对更多影响索导管倾角的因素进行合理准确的量化分析,可为斜拉索施工提供可靠的技术支撑。