黏声TTI介质中纯qP波逆时偏移成像方法
慕鑫茹 黄建平 黎国龙 毛强


摘要:地下介质广泛存在黏滞性及各向异性特征,使得地震波在传播过程中发生相位畸变和振幅衰减。若在偏移成像时不对这些黏滞性及各向异性影响进行校正,则会引入成像噪声而降低成像分辨率。针对上述问题,首先将黏滞性引入到TTI介质波动方程,得到一种黏声TTI介质纯qP波波动方程。然后,基于新推导的黏声TTI介质波动方程,发展相应的逆时偏移成像方法。由于黏滞性补偿过程中能量会被放大,波场中指数增加的高频噪声易造成波场传播不稳定。鉴于此,将正则化算子引入到逆时能量补偿过程,以压制波场中的高频噪声。结果表明:新提出的黏声TTI介质逆时偏移成像算法可校正相位畸变,补偿能量衰减,实现对含黏滞性及各向异性介质的高精度成像。
关键词:黏声TTI介质; 有限差分-伪谱法; 正则化算子; 逆时偏移
中图分类号:P 631.4 文献标志码:A
引用格式:慕鑫茹,黄建平,黎国龙,等.黏声TTI介质中纯qP波逆时偏移成像方法[J].中国石油大学学报(自然科学版),2023,47(2):44-52.
MU Xinru, HUANG Jianping, LI Guolong, et al. Reverse time migration in viscoacoustic TTI media based on pure qP wave equation[J]. Journal of China University of Petroleum(Edition of Natural Science), 2023,47(2):44-52.
Reverse time migration in viscoacoustic TTI media based on pure qP wave equation
MU Xinru1,2, HUANG Jianping1,2, LI Guolong1,2, MAO Qiang1,2
(1.School of Geosciences in China University of Petroleum (East China), Qingdao 266580, China; 2.Pilot National Laboratory for Marine Science and Technology(Qingdao), Qingdao 266071, China)
Abstract:During seismic wave propagation, phase distortion and amplitude attenuation occur due to the anisotropy and viscosity of the underground media. Failure to correct for these effects during migration imaging can lead to reduced imaging resolution and the introduction of imaging noise. To address this, we introduce viscosity into the anisotropic wave equation and obtain a pure qP wave equation in viscoacoustic TTI media. We then develop a reverse time migration imaging method based on the wave equation of viscoacoustic TTI media. The exponential increase of high-frequency noise in the wave field during viscosity compensation can cause wave propagation instability. To mitigate this issue, we introduce a stable regularization operator into the energy compensation process to suppress the high-frequency noise. Numerical tests show that the new wave equation accurately simulates wave propagation characteristics in viscous and anisotropic media. In addition, the proposed reverse time migration imaging algorithm for viscoacoustic TTI media corrects travel time error and phase distortion, compensates for energy attenuation, and achieves high-precision imaging of underground complex media with anisotropy and viscosity.
Keywords:viscoacoustic TTI media; finite difference and pseudo spectral method; regularization operator; reverse time migration
中国西部地区地下介质组成复杂,广泛分布各向异性和黏滞性[1-3]。如页岩地层表现出各向异性[4],浅层天然气烟囱表现出黏滞性[5],而充填流体的裂缝地层则同时表现出黏滞性和各向异性特征[3]。若在偏移成像时忽略这些黏滞性及各向异性影响则会造成成像结果中同相轴不能准确归位且能量较弱,从而降低成像分辨率。因此发展能准确、高效、稳定地模拟地下介质中波传播的方程是速度反演及偏移成像的基础。Thomsen各向异性参数的引入方便了各向异性性质的描述并推动了各向异性理论的快速发展[6]。由于多分量弹性波数据采集成本高,当前地震勘探仍以纵波为主[4,7-9]。此外,各向异性弹性波方程由于其数值模拟计算量大且波场分离困难,发展准确稳定的各向异性声波动方程是当前的研究热点[10-11]。基于声学假设推导的不同形式的各向异性声波方程可分为传统的耦合拟声波方程和纯qP波方程。前者可从精确的频散方程或者本构关系出发[12-14],计算效率高,且其只做了一次声学假设,模拟波场传播的精度高,但模拟的波场存在伪横波干扰,且在各向异性参数ε<δ时不稳定。后者[3,15-18]从精确相速度公式出发,模拟的波场没有伪横波干扰,且在各向异性参数ε<δ数值模拟仍然稳定,但其在推导过程中除做了声学假设外还做了其他近似(如最小二乘近似或泰勒近似),因此其波场模拟精度低于耦合拟声波方程。早期的黏滞性衰减补偿工作基于一维反Q滤波[19],但这种黏滞性补偿方法没有考虑波场传播路径的影响,精度较低。因此Carione等[20-21]提出基于标准线性固体模型或者常Q模型的波动方程,并应用于速度反演及偏移成像中。线性固体模型的组合数量越多,对黏滞性的描述也越精确。基于标准线性固体模型推导的黏声波动方程可用有限差分求解,具有计算效率高的优点。但是其振幅衰减项与相位频散项是耦合在一起的,当组合的线性固体模型较多时,振幅衰减与相位频散的解耦也愈加困难,不便于实现逆时偏移成像[22]。基于常Q模型推导的黏声波动方程具有解耦的振幅衰减项与相位频散项,可便于实现逆时偏移成像,但是这类波动方程通过时间分数阶或者空间分数阶表示,而时间分数阶和空间分数阶的数值求解困难且計算量大[23-26]。地下介质中的黏滞性和各向异性往往是同时存在的,且黏滞性也通常表现出各向异性特性[3,27-31]。为了满足实际生产需求,多种黏滞性各向异性波动方程及相应的偏移成像方法被提出并得到应用[27-31]。这些黏声各向异性波动方程基于不同的各向异性及黏滞性理论推导而来,相应地继承了不同黏滞性及各向异性波动方程的优缺点。例如,Mu等[3]结合各向异性纯qP波方程和常Q衰减模型发展了一种空间分数阶算子表示的黏声各向异性波动方程。这种波动方程无伪横波干扰,在各向异性参数ε<δ时数值模拟稳定。此外,其包含了解耦的振幅衰减项及相位频散项,方便实现逆时偏移成像。在实现黏声逆时偏移成像时,逆时反传的波场中的高频能量会呈指数形式增加,这种指数增加的高频噪声会造成波场不稳定。低通滤波是一种简单有效的方法,但应用于复杂模型时会造成有效信号的滤除[27-28]。此外,也可以通过引入正则化算子来压制高频噪声[31]。通过最小二乘逆时偏移成像来压制高频噪声精度较高,但是需要多次迭代,计算量较大[21]。最近提出的一种通过向逆时延拓波场传播算子引入频率调节因子的稳定性策略不仅可以保证波场的稳定模拟,还可以压制波场中的随机噪声,得到更加精确的成像结果[28]。笔者结合标准线性固体衰减模型和TTI介质纯qP波方程,推导一种新的黏声各向异性波动方程及相应的偏移算子,并通过正则化算子的引入来压制黏声波场反传中的高频噪声。
1 方法原理
1.1 黏声波方程
基于标准线性固体模型的波动方程由于其耦合的振幅衰减项与相位频散项,逆时偏移实现困难。因此Li等[25]基于标准线性固体模型的频散关系式,发展了一种振幅衰减项与相位频散解耦的黏声波动方程
在方程(1)中,第二项表示振幅衰减,第三项表示相位频散。忽略相位频散影响,可以得到仅考虑振幅衰减的黏声波动方程
3 模型测试
3.1 均匀模型
首先选取一个均匀各向异性模型来验证各向异性黏声波方程(6)和(7)的正确性及有效性。模型尺寸为4 000 m×4 000 m,网格大小为dx=dz=10 m。该模型具有恒定的黏滞性及各向异性参数值,分别为v=2 600 m/s,ε=0.18,δ=0.23,φ=30°。在模型中央激发主频25 Hz的Ricker子波。数值模拟采用的时间步长为0.8 ms。在空间位置(3 000 m,3 000 m)处放一个检波器,并记录时间长度为0.72 s的波场值。
图1为分别使用声波方程(图1(a))、黏声波方程(图1(b))、各向异性声波方程(图1(c))及黏声各向异性方程(图1(d))模拟的0.4 s时刻的波场快照。与TTI声波方程模拟的波场(图1(c))相比,黏声TTI方程模拟的波场(图1(d))能量较弱,但是两种方程模拟的波场的波前面形态一致。这种能量损失很好地描述了地震波在黏滞性介质中传播的能量衰减特征。黏声TTI方程模拟的波场(图1(d))与黏声波方程模拟的波场(图1(b))的波前面形态差别很大,但是其能量几乎完全一致。这表明了黏声TTI方程可以模拟与黏声波方程相似的能量衰减过程。
图2(a)展示了不同波动方程模拟时,位于(3 000 m,3 000 m)处的检波器记录的波形信息。从图2(a)中可以看出,考虑各向异性后波场走时发生了明显变化,沿着各向异性倾角方向传播速度更快。无论对各向同性还是各向异性方程,考虑黏滞性后其波场走时保持不变,但振幅能量明显减小。图2(b)为图2(a)中相应波形的频谱图。在没有黏滞性影响时,各向同性和各向异性声波方程具有相同的频带宽度,且各个频率成分的振幅几乎一致。当引入黏滞性影响时,黏声各向异性模拟的波场与黏声各向同性模拟的波场频率成分均发生了降低,但频带宽度仍然一致,各个频率成分的振幅很接近。这些均表明了本文中新提出的黏声TTI波动方程可以描述地震波在黏滞性和各向异性介质中传播时的振幅衰减和走时畸变特征,为逆时偏移成像提供了一个很好的理论方程基础。
3.2 正则化算子测试
为了测试正则化算子的正确性,设计一个两层模型,如图3(a)所示,模型大小为3 000 m×2 000 m。该试验中使用黏声TTI介质逆时反传波场传播算子计算波场值。图3(b)为未添加正则化项的逆时反传波场快照,波场中存在着明显的高频噪声,这些高频噪声几乎将有效信號完全湮没。图3(c)展示了使用添加正则化项的波场传播算子模拟的波场,波场模拟稳定,没有任何噪声。此处使用的正则化参数为σ=0.1。
3.3 气云模型
为验证逆时偏移成像算法的有效性,建立了一个简单的气云模型,如图4所示。模型大小为4 000 m×2 000 m,水平方向和垂直方向的网格间距均为10 m。正演时将81炮等间隔布设于地表,并使用401道位于地表的检波器接收来自地下的反射信号。主频为25 Hz的雷克子波作为激发震源,时间采样间隔为0.8 ms,总的记录时长为1.6 s。
逆时偏移成像结果如图5所示,其中图5(a)为采用TTI声波正演模拟得到的炮记录进行TTI声波逆时偏移成像得到的成像结果,此处被用于黏声波逆时偏移的参考。图5(b)、(c)分别为使用声波TTI逆时偏移和黏声波TTI逆时偏移成像算子(稳定因子σ=0.1)对用黏声波方程正演得到的炮记录做成像得到的结果。由于没有进行能量补偿,使用TTI声波偏移算子得到成像结果(图5(b))比参考结果深部振幅能量较弱,尤其气云结构下方地层。若考虑黏滞性影响,得到的偏移成像结果(图5(c))深部地层同相轴能量得到有效恢复。
3.4 BP 2004模型
为进一步测试本文中提出的黏声各向异性逆时偏移成像算法在复杂介质中的有效性。参考Mu等[3]修改的黏滞性及各向异性参数场,如图6所示。该模型尺寸大小为4 500 m×2 250 m,水平及垂直方向的网格间距均为10 m。模型的浅部中央部分包含一个具有强衰减性质的气藏结构。先基于该模型生成用于逆时偏移的黏声各向异性炮记录,该过程使用方程(8)和(9)计算。时间采样间隔为0.8 ms,总的记录时长为2.6 s。震源选用主频为25 Hz的雷克子波。91炮均匀地布置于地表,且炮间隔为50 m。位于地表的451个检波器用于接收反射波场,接收间隔为10 m。偏移速度模型通过对图6使用高斯平滑得到,且在偏移前做去直达波处理。
图7为逆时偏移成像结果。首先使用声波TTI正演得到炮记录,然后将声波TTI偏移算子应用于得到的炮记录,得到的成像剖面为参考结果(图7(a))。图7(b)为应用声TTI偏移算子于先前生成的黏滞性各向异性炮记录中得到的结果。由于未校正黏滞性衰减影响,得到的成像结果的同相轴能量相比参考剖面较弱,尤其是气藏下边的地层。如图7(c)所示,当考虑黏滞性衰减影响后,深部同相轴能量得到补偿,分辨率更高。为了更加清晰地显示振幅补偿效果,将图7(a)~(c)中红色矩形框内的波场进行放大显示,放大结果如图7(d)~(f)。对比图7(d)~(f),可以清晰地观察到使用黏滞性各向异性偏移算子的成像结果的能量得到补偿。
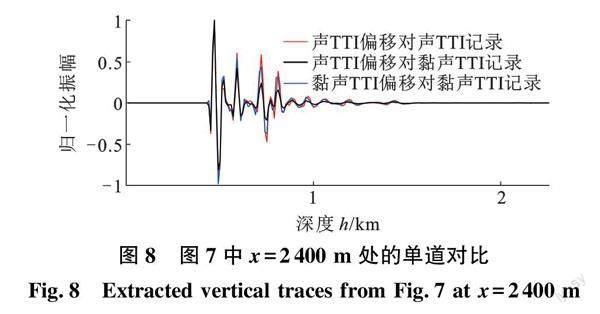
为更加详细地说明黏滞性各向异性逆时偏移成像的正确性及有效性,提取图7中偏移距为2.4 km处的单道记录(图8)。与红色实线相比(参考道),黑色实线的振幅发生明显衰减,然而蓝色实线与红色实线振幅几乎一致。这表明,本文中提出的黏声各向异性逆时偏移成像算法可以校正黏滞性及各向异性影响,得到高分辨率的成像结果。
4 结束语
将黏滞性振幅衰减影响拓展到TTI介质纯qP波方程,改进了黏滞性及各向异性介质的正演模拟及逆时偏移成像算法。新的黏声TTI波动方程无伪横波干扰,且在各向异性参数ε<δ时数值模拟仍稳定。此外,该方程具有解耦的振幅衰减项,方便衰减补偿逆时偏移成像的实施。在逆时偏移的波场反传过程中,通过引入一种稳定的正则化算子来消除指数形式增长的高频噪声,进而保证逆时偏移成像的稳定。数值模拟测试表明新提出的黏滞性及各向异性逆时偏移成像算法可校正各向异性影响,补偿能量衰减,得到高精度的成像结果。
参考文献:
[1] 吴国忱.各向异性介质地震波传播与成像[M].东营:石油大学出版社,2006:1-60.
[2] 李振春,郭振波,田坤.黏声介质最小平方逆时偏移[J].地球物理学报,2014,57(1):214-228.
LI Zhenchun, GUO Zhenbo, TIAN Kun. Least-squares reverse time migration in visco-acoustic medium[J].Chinese Journal of Geophysics, 2014,57(1):214-228.
[3] MU X, HUANG J, YANG J, et al. Modeling of pure visco-qP-wave propagation in attenuating tilted transversely isotropic media based on decoupled fractional Laplacians[J]. Geophysics, 2022,87(4):T291-T313.
[4] 黄金强,李振春.基于Low-rank分解的复杂TI介质纯qP波正演模拟与逆时偏移[J].地球物理学报,2017,60(2):704-721.
HUANG Jinqiang, LI Zhenchun. Modeling and reverse time migration of pure quasi-P-waves in complex TI media with a low-rank decomposition[J].Chinese Journal of Geophysics, 2017,60(2):704-721.
[5] 豆辉,徐逸鹤.黏性逆时偏移成像研究进展[J].地球物理学进展,2019,34(5):1866-1877.
DOU Hui, XU Yihe. Progress in the Q-compensated reverse time migration imaging[J]. Progress in Geophysics, 2019,34(5):1866-1877.
[6] THOMSEN L. Weak elastic anisotropy[J]. Geophysics, 1986,51(10):1954-1966.
[7] MU X, HUANG J, YONG P, et al. Modeling of pure qP-and qSV-waves in tilted transversely isotropic media with the optimal quadratic approximation[J]. Geophysics, 2020,85(2):C71-C89.
[8] 李振春,雍鹏,黄建平,等.基于矢量波场分离弹性波逆时偏移成像[J].中国石油大学学报(自然科学版),2016,40(1):42-48.
LI Zhenchun, YONG Peng, HUANG Jianping, et al. Elastic wave reverse time migration based on vector wave field separation[J]. Journal of China University of Petroleum (Edition of Natural Science), 2016,40(1):42-48.
[9] 黃建平,杨宇,李振春,等.基于M-PML边界的Lebedev网格起伏地表正演模拟方法及稳定性分析[J].中国石油大学学报(自然科学版),2016,40(4):47-56.
HUANG Jianping, YANG Yu, LI Zhenchun, et al. Lebedev grid finite difference modeling for irregular free surface and stability analysis based on M-PML boundary condition[J]. Journal of China University of Petroleum (Edition of Natural Science), 2016,40(4):47-56.
[10] ALKHALIFAH T. An acoustic wave equation for anisotropic media[J]. Geophysics, 2000,65(4):1239-1250.
[11] TSVANKIN I. P-wave signatures and notation for transversely isotropic media:an overview[J]. Geophysics, 1996,61(2):467-483.
[12] DUVENECK E, BAKKER P M. Stable P-wave modeling for reverse-time migration in tilted TI media[J]. Geophysics, 2011,76(2):S65-S75.
[13] ZHANG Y, ZHANG H, ZHANG G. A stable TTI reverse time migration and its implementation[J]. Geophysics, 2011,76(3):WA3-WA11.
[14] FLETCHER R P, DU X, FOWLER P J. Reverse time migration in tilted transversely isotropic (TTI) media[J]. Geophysics, 2009,74(6):WCA179-WCA187.
[15] CHU C, MACY B K, ANNO P D. Pure acoustic wave propagation in transversely isotropic media by the pseudospectral method[J]. Geophysical Prospecting, 2013,61(3):556-567.
[16] 程玖兵,康瑋,王腾飞.各向异性介质qP波传播描述I:伪纯模式波动方程[J].地球物理学报,2013,56(10):3474-3486.
CHENG Jiubing, KANG Wei, WANG Tengfei. Description of qP-wave propagation in anisotropic media, Part Ⅰ: pseudo-pure-mode wave equations[J]. Chinese Journal of Geophysics, 2013,56(10):3474-3486.
[17] 慕鑫茹,黄建平,李振春,等.基于最佳平方逼近的TTI介质解耦qP波与qSV波逆时偏移[J].石油地球物理勘探,2019,54(6):1280-1292.
MU Xinru, HUANG Jianping, LI Zhenchun, et al. Reverse time migration of decoupled qP- and qSV-waves in TTI media with the optimal quadratic approximation[J]. Oil Geophysical Prospecting, 2019,54(6):1280-1292.
[18] 徐世刚,包乾宗,任志明,等.结合泊松算法和波场分解成像条件的各向异性优化纯声波方程逆时偏移[J].石油地球物理勘探,2022,57(3):613-623.
XU Shigang, BAO Qianzong, REN Zhiming, et al. Reverse-time migration of optimized pure acoustic equation in anisotropic media by combining Poisson algorithm and wavefield decomposition imaging condition[J]. Oil Geophysical Prospecting, 2022,57(3):613-623.
[19] WANG Y. A stable and efficient approach of inverse Q filtering[J]. Geophysics, 2002,67(2):657-663.
[20] CARCIONE J M. Wave fields in real media:wave propagation in anisotropic, anelastic, porous and electromagnetic media[M]. Amsterdam: Elsevier, 2007:99-103.
[21] DUTTA G, SCHUSTER G T. Attenuation compensation for least-squares reverse time migration using the viscoacoustic-wave equation[J]. Geophysics, 2014,79(6):S251-S262.
[22] WANG N, ZHU T, ZHOU H, et al. Fractional Laplacians viscoacoustic wavefield modeling with k-space-based time-stepping error compensating scheme[J]. Geophysics, 2020,85(1):T1-T13.
[23] MU X, HUANG J, WEN L, et al. Modeling viscoacoustic wave propagation using a new spatial variable-order fractional Laplacian wave equation[J]. Geophysics, 2021,86(6):T487-T507.
[24] ZHU T, CARCIONE J M, HARRIS J M. Approximating constant-Q seismic propagation in the time domain[J]. Geophysical Prospecting, 2013,61(5):931-940.
[25] LI Q, FU L Y, ZHOU H, et al. Effective Q-compensated reverse time migration using new decoupled fractional Laplacian viscoacoustic wave equation[J]. Geophysics, 2019,84(2):S57-S69.
[26] CHEN H, ZHOU H, LI Q, et al. Two efficient modeling schemes for fractional Laplacian viscoacoustic wave equation[J]. Geophysics, 2016,81(5):T233-T249.
[27] QU Y, HUANG J, LI Z, et al. Attenuation compensation in anisotropic least-squares reverse time migration[J]. Geophysics, 2017,82(6):S411-S423.
[28] MU X, HUANG J, LI Z, et al. Attenuation compensation and anisotropy correction in reverse time migration for attenuating tilted transversely isotropic media[J]. Surveys in Geophysics, 2022:1-37.
[29] ZHU T, BAI T. Efficient modeling of wave propagation in a vertical transversely isotropic attenuative medium based on fractional Laplacian[J]. Geophysics, 2019,84(3):T121-T131.
[30] QIAO Z, SUN C, TANG J. Modelling of viscoacoustic wave propagation in transversely isotropic media using decoupled fractional Laplacians [J]. Geophysical Prospecting, 2020,68(8):2400-2418.
[31] ALI F, DANIEL O T, KRISTOPHER A I. Q-compensated reverse time migration in tilted transversely isotropic media [J]. Geophysics, 2021,86(1):S73-S89.
(編辑 修荣荣)
收稿日期:2022-07-28
基金项目:“十四五”重大项目(2021QNLM020001);国家重点研发计划(2019YFC0605503C); 优秀青年科学基金项目(41922028); 国家创新群体项目(41821002); 中石油重大科技项目(ZD2019-183-003)
第一作者及通信作者:慕鑫茹 (1995-),男,博士研究生,研究方向为黏滞性及各向异性介质地震波偏移成像。E-mail: xinrumu@126.com。

