跨声速自然层流标模CRM-NLF 风洞试验快速转捩预测

刘银辉，吴东润，杜 玺，林大楷

(1.中国商用飞机有限责任公司 北京民用飞机技术研究中心，北京 102211；2.民用飞机设计数字仿真技术北京市重点实验室，北京 102211)

0 引言

层流设计能给飞机带来十分显著的减阻收益[1]。研究表明，如果将层流设计成功应用于机翼、发动机短舱、水平尾翼和垂直尾翼等部件，具有减少15%整机阻力的潜力，其中机翼采用层流设计带来的收益最显著，具有减少10%整机阻力的潜力。根据Arcara等[2]的估算，如果民机能在主翼上翼面、垂尾和平尾上实现50%弦长的层流覆盖，在发动机短舱上实现40%弦长的层流覆盖，巡航升阻比可提升14.7%，从而可以降低对应方案起飞总重量的9.9%、操作空重的5.7%。现役大型民用飞机中，波音787 的短舱[3]以及波音737 Max[4]的翼梢小翼采用了层流设计，如图1 所示。这标志着先进的飞机制造技术已经可以一定程度上满足层流设计的要求。开展层流设计研究，逐步推进飞机各部件的层流应用，是保证大型民用飞机具有气动性能优势的重要手段之一。

图1 层流飞机[4]Fig.1 Laminar aircraft[4]

边界层转捩预测是CFD 最具挑战的难题之一。高效可靠的转捩预测分析是飞机层流设计的关键。工程上常用的转捩预测方法分为两类：基于RANS 的转捩模型方法和eN方法。对于第一类方法，随着对转捩物理机理认知的逐渐深入和试验数据的不断丰富，转捩模型已取得丰硕的研究成果。2021 年第一届AIAA RANS 转捩模型和预测会议中，针对标模ERCOFTAC T3 平板、NLF(1)-0416 翼型、6∶1 椭球体和CRM-NLF 机翼，十余家单位采用不同的转捩方法进行了转捩预测，但预测的转捩位置偏差较大[5]。目前，文献公开发表的基于RANS 方程的转捩模型已多达几十种。其中比较著名的有：基于间歇因子的转捩模型方法，如 γ-Reθ[6-8]等；基于物理机理的层流动能转捩模型，如kT-kL-ω[9-10]、k-ω-γ[11-13]等。总之，基于间歇因子的转捩模型高度依赖于试验数据的经验拟合，对转捩前区域的物理机制考虑不足，适用范围有限；基于层流动能的转捩模型能较为充分地考虑转捩过程的物理机理，然而，现有基于层流动能的转捩模型难以解析地给出三维边界层流动的转捩起始位置和转捩过程[14]。这些转捩模型有待进一步改进，从而准确预测工程上三维复杂外形的边界层转捩。

第二类是eN方法。eN方法一般是对数值计算（如直接数值模拟、带转捩的RANS 等）得到的层流基本流进行稳定性分析获得N值包络线。基于线性稳定性理论的半经验eN方法仍然是飞机设计计算中得到最广泛认可的转捩预测方法[15]，它通过扰动幅值放大因子N判断转捩的发生。相比二维和轴对称边界层，针对复杂三维外形开展的研究相对较少。基于eN方法进行三维边界层转捩分析的难点在于展向波参数和积分路径的选取等，比较常用的方法包含时间模式包络法、鞍点法、固定展向波数法和双eN法等。时间模式包络法的N值采用时间模式沿群速度方向积分获得，如Malik 开发的转捩软件COSAL[16]。鞍点法最早由Cebeci 和Stewartson[17]提出，扰动沿群速度方向传播，通过固定频率对不同展向波数下的最大增长率进行积分计算N值，然后再计算频率的N值包络，相对保守。天津大学团队在超声速/高超声速边界层中开展了简化鞍点法、基于内波理论提出射线跟踪法、一般三维边界层广义增长率守恒关系等[18-22]方面的工作，并开发了对应的转捩预测软件。固定展向波数法，适用于无限展长后掠平板和后掠翼型等，扰动展向波数不变，得出不同展向波数和频率下的N值包络线。Malik 等[23]发现，假定无黏势流方向的展向波数为实数，扰动增长率沿无黏势流方向进行N值计算，计算量小且精度足够。基于Malik 等[23]的发现，可以进一步分别对Tollmien-Schlichting（T-S）模态和横流（CF）模态进行N值计算，这种方法被称作双eN方法。T-S 模态无黏势流方向和群速度方向夹角一般不超过5°，T-S 模态采用固定波角法（无黏势流方向的展向波数为0）或无黏势流方向的展向波数取较小的实数进行N值计算，而CF 模态采用固定展向波数法进行N值计算，如NASA 的eMalik[24]和LASTRAC[25]，以及西北工业大学的韩忠华等[26]发展的翼身组合体转捩自动判断方法等。为了提高计算效率，后续文献基于eN方法提出了简化的eN数据库转捩预测方法[27-31]。本文采用eN方法进行跨声速转捩预测分析，简化的eN数据库方法不再赘述。

eN方法需CFD 求解器提供层流基本流计算的边界层信息，一般地，基于RANS 的CFD 工具普遍存在计算周期过长、一些情况下解的精度或可靠性不足、CFD 用户技能水平差异大[32]等问题。因此，中国商飞北研中心开发了面向工程应用的快速CFD 分析工具CFAST，基于试验转捩位置设置CFD 转捩点，转捩点前的流场为层流基本流，单工况的计算时间仅为200 s，大幅缩短计算周期。本文研究对象是NASA的跨声速高雷诺数自然层流标模CRM-NLF[33]。首先，基本流场由CFAST 得出；然后，采用基于线性稳定性理论的eN方法进行转捩预测分析，为层流机翼设计和优化提供理论依据和参考。下面对研究模型、快速CFD 分析工具CFAST 和eN方法进行简介，并基于标模NLF(2)-0415 对计算结果进行验证。

1 研究模型和数值方法

1.1 标模CRM-NLF 简介

自然层流标模CRM-NLF 是美国NASA 近年来采用跨声速自然层流超临界机翼设计的翼身组合体标模，进行了变迎角、变雷诺数的高雷诺数风洞试验验证，得到超临界自然层流机翼的边界层转捩特性，并公开了其几何模型、CFD 计算结果、试验数据等[33-34]。标模CRM-NLF 转捩由横流驻波模态和T-S 模态主导，其设计目标是在飞机的巡航马赫数、雷诺数和后掠角范围内尽可能扩大层流区。图2 展示了风洞试验模型。图3 展示了机翼沿展向的测试站位。图4 展示了机翼典型压力分布设计示意图，压力分布在前缘具有快速加速区，抑制横流模态的增长，之后保持机翼中段为弱顺压梯度区，抑制T-S 模态增长。前缘横流模态和机翼中段T-S 模态扰动抑制是层流设计的关键，标模CRM-NLF 试验结果表明以层流区弦向长度为特征长度的转捩雷诺数最高可达1 000 万。

图2 CRM-NLF 风洞试验模型[34]Fig.2 Test model of CRM-NLF[34]

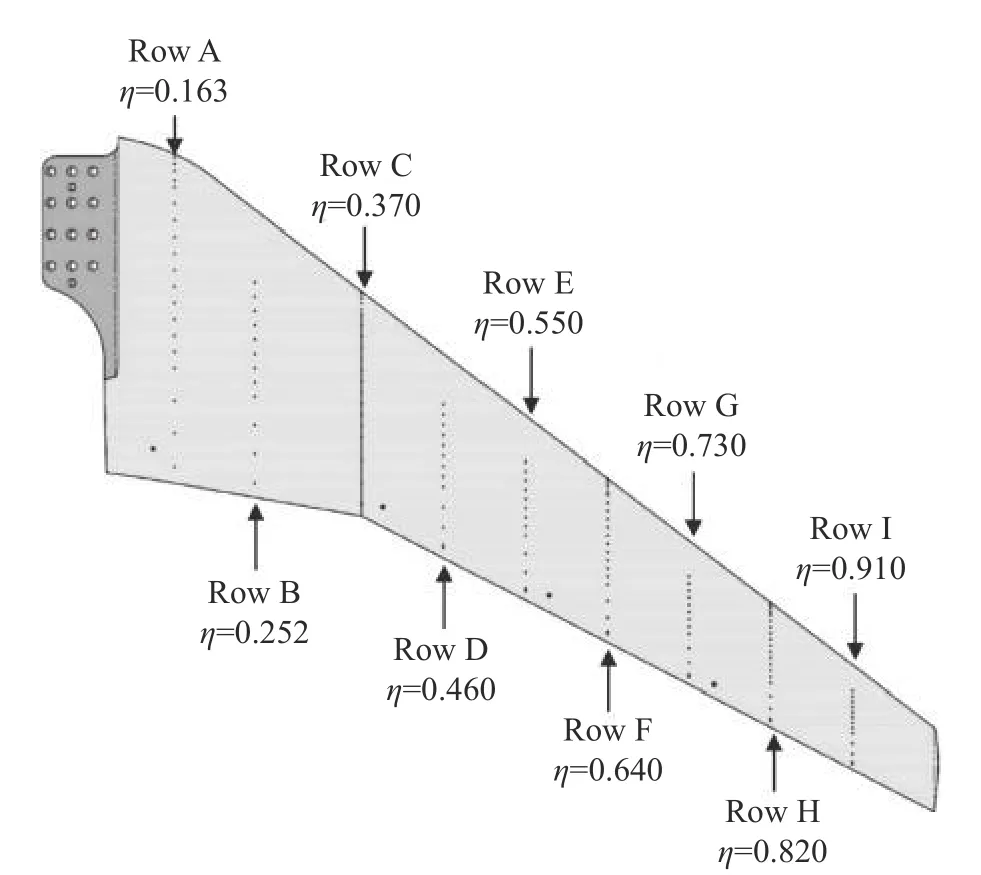
图3 CRM-NLF 翼展位置示意图[34]Fig.3 Spanwise stations of the CRM-NLF model[34]

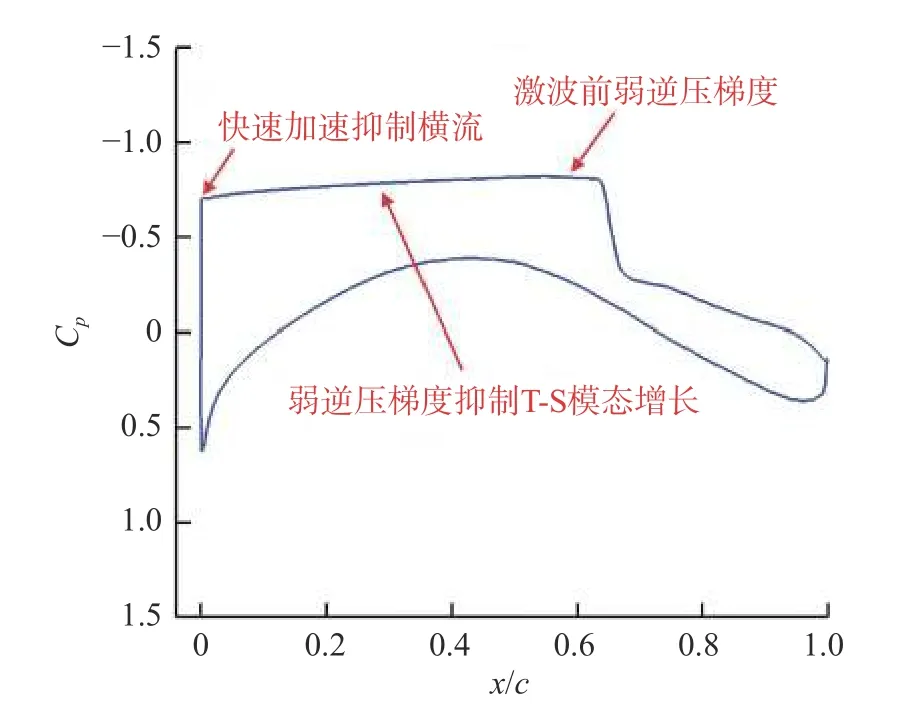
图4 机翼的典型压力分布[34]Fig.4 Representative pressure distribution of the CRM-NLF model[34]

1.2 定常流场分析工具CFAST 简介

CFAST 是中国商飞北研中心开发的面向工程应用的CFD 快速分析工具。采用嵌套网格，机身构造背景网格、机翼单独划分C 型网格，边界层外流场采用欧拉控制方程求解。边界层单独划分求解域，采用曲面非正交坐标系，通过Keller-Box 转化边界层方程组为6 个常微分方程，利用预测-修正格式推进求解。边界层计算流程如下：在翼根和机翼驻线交点，首先按无限后掠翼假设给出初始值，之后沿翼根推进求解驻线至翼梢，最后自驻点起始，沿流线完成边界层全场计算。边界层流场向无黏外流流场输出溢出速度，使无黏外流在机翼表面的流向偏离物面，用于描述边界层对流动的堵塞作用。CFAST 自驻点开始层流基本流计算，根据指定的强制转捩位置转捩，之后为湍流计算，湍流平均流动应用零方程Cebeci-Smith 模型模拟。强制转捩位置略大于试验转捩位置，保证试验转捩位置前的流场为层流。CFAST 在个人计算机上单一工况的计算时间仅约200 s，该计算速度主要是通过小量级网格的外流无黏与边界层修正迭代完成的。由于边界层计算域推进求解一轮比无黏外流迭代求解一步的时间长数倍，因此在多步无黏外流迭代后才执行一次边界层计算域的计算，即边界层修正。典型的翼身嵌套网格总数为100 万量级，典型的计算收敛步数为60 步。图5 给出了残差收敛曲线，在网格残差突变位置完成边界层修正，残差突变是边界层输出到外流的溢出速度更新导致的，该突变引起的残差上升很快，在2～3 个迭代步后即可消除。

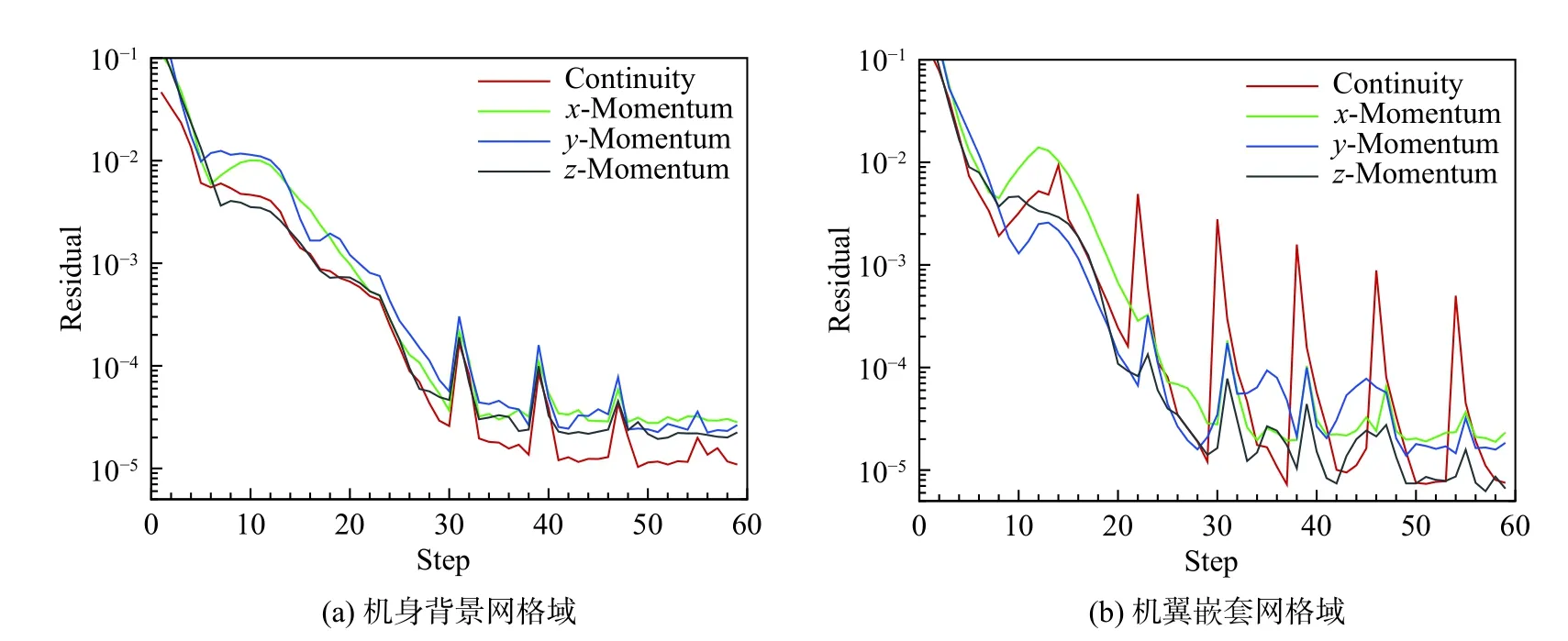
图5 标模CRM-NLF 残差收敛历程图Fig.5 Residual convergence history diagram of the standard model CRM-NLF

在边界层修正步，边界层自驻点出发，沿流向求解边界层方程并输出边界层速度、温度、密度法向分布，为eN分析提供了所需的三维可压缩边界层信息。其中典型的密度和三维速度分布如图6 所示。

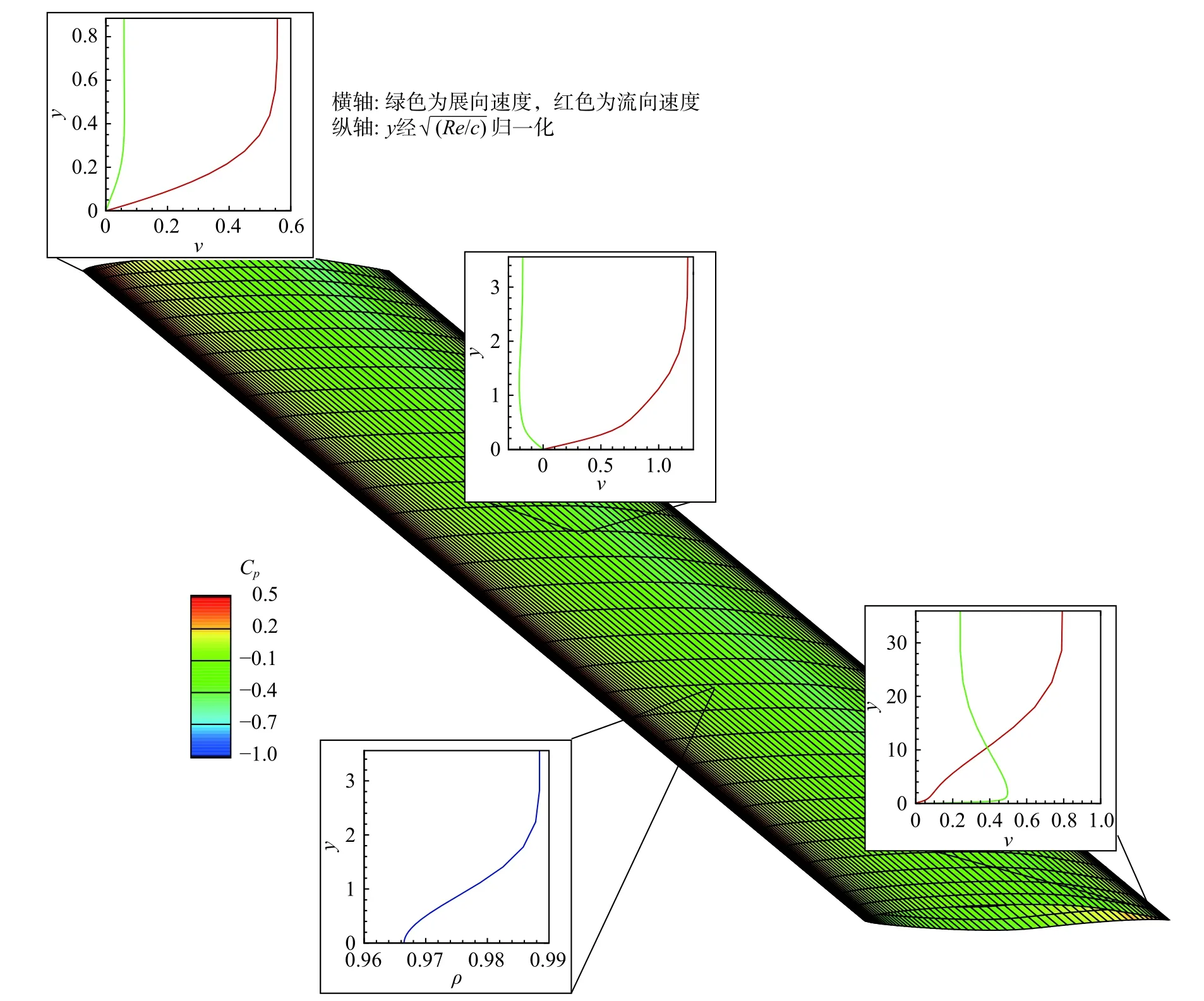
图6 三维可压缩边界层信息Fig.6 Boundary layer characteristics of three-dimensional compressible flow

1.3 转捩预测的eN方法简介

基于线性稳定性理论的eN方法仍然是目前飞机设计计算中得到最广泛认可的转捩预测方法。eN方法的基本思想是，边界层内存在的各种频率的小幅值扰动波向下游传播，扰动从开始放大处起，沿下游方向对其线性增长率做积分，取其包络线，从而得到N值，再通过试验等手段对N值进行标定，确定转捩判据。在所有频率的扰动中，扰动的N值包络最先达到转捩判据的位置被认为是转捩位置。不稳定模态扰动幅值满足如下关系式：

式中：A为 扰动幅值；A0为扰动开始放大处的幅值；N与幅值增长倍数有关，一般认为N是扰动频率和流向位置的函数；αi为扰动增长率。

Malik 等[23]发现，假定无黏势流方向的展向波数为实数，扰动增长率沿无黏势流方向进行N值计算，计算量小且精度足够。本文eN积分路径选取与无黏势流方向保持一致。通常情况下，对于当前跨声速大型民用飞机典型后掠机翼表面三维流动问题，转捩由T-S 模态和横流驻波模态共同主导。本文基于线性稳定性理论的双eN方法对N进行转捩预测分析，双eN方法的描述详见文献[26]。对于T-S 模态，采用固定波角法，沿着无黏势流方向对增长率进行积分获得不同频率下的N值包络线；对于横流驻波模态，频率取0，采用固定展向波数法，获得不同展向波数下的N值包络线。

1.4 算例验证

选取标模NLF(2)-0415，图7 对比展示了Re=2.37×106、迎角为-4°时计算和试验结果[35]，由图可知，本文CFAST 计算结果与试验结果基本吻合，说明CFAST 能准确得出基本流结果。

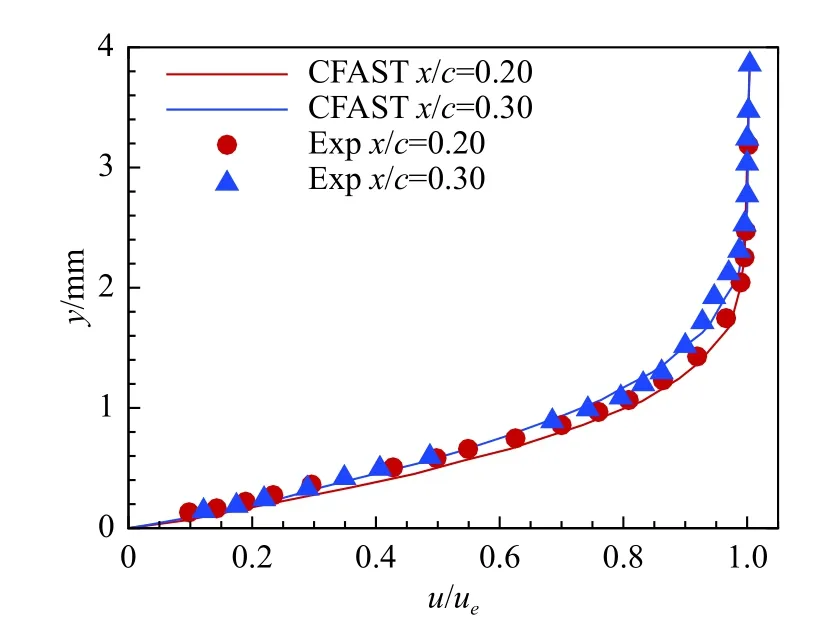
图7 以当地外缘速度无量纲化的流向速度分布Fig.7 Wall-normal profiles of the streamwise velocity

2 计算参数与网格设置

采用CFAST 完成无黏外流和边界层耦合计算，机翼下表面全湍流，上表面基于CRM-NLF 的低湍流风洞试验结果[33]，选取15 个不同展向位置，结合试验转捩点给定强制转捩位置。计算设置的强制转捩点较试验转捩点向后延长了2%弦长，便于eN分析计算试验转捩点的N值。不同展向网格对应站位η的转捩点由给定的强制转捩位置插值拟合得出，其中η表示展向站位距机身轴线距离与翼梢距机身轴线距离之比。具体计算工况参见表1。

表1 计算工况Table 1 Calculated parameters

本文无黏外流网格设置如图8（a）所示，网格总数110 万。机翼边界层第一层网格高度1.1×10-7m，法向增长率1.26，边界层内法向网格点数沿弦向逐渐增长，前缘处为21，尾缘处增至46，以满足边界层厚度沿弦向的增长需求，机身不计算边界层。Venkatachari等[36]基于RANS 计算网格设置如图8（b）所示，网格总数1.2 亿，边界层第一层网格高度2.54×10-6m，法向增长率1.02，法向网格数200，边界层内网格数约40，机身计算边界层。

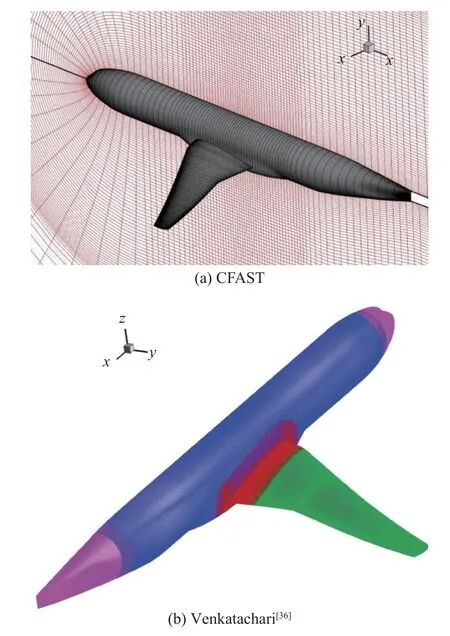
图8 网格分布Fig.8 Grid distribution

3 结果与分析

3.1 基本流场

图9 展示了CFAST 带转捩计算获得的俯视表面压力系数Cp云图，并与Paredes 等[37]的计算结果进行了对比，CFAST 半模计算给出了左侧机身，Paredes等[37]给出了右侧机身，两者的结果具有相同的变化特征，翼根先向外伸出第一道激波，机翼拐折后，外翼段存在第二道激波。固定迎角变雷诺数（Case 1 和Case 2）时，激波的形态保持一致，激波线基本不变；固定雷诺数变迎角（Case 1 和Case 3）时，随迎角的增大，内翼段展向向外延伸出的激波更长，激波有较明显的变化。Case 2 和Case 3 的结果图类似。

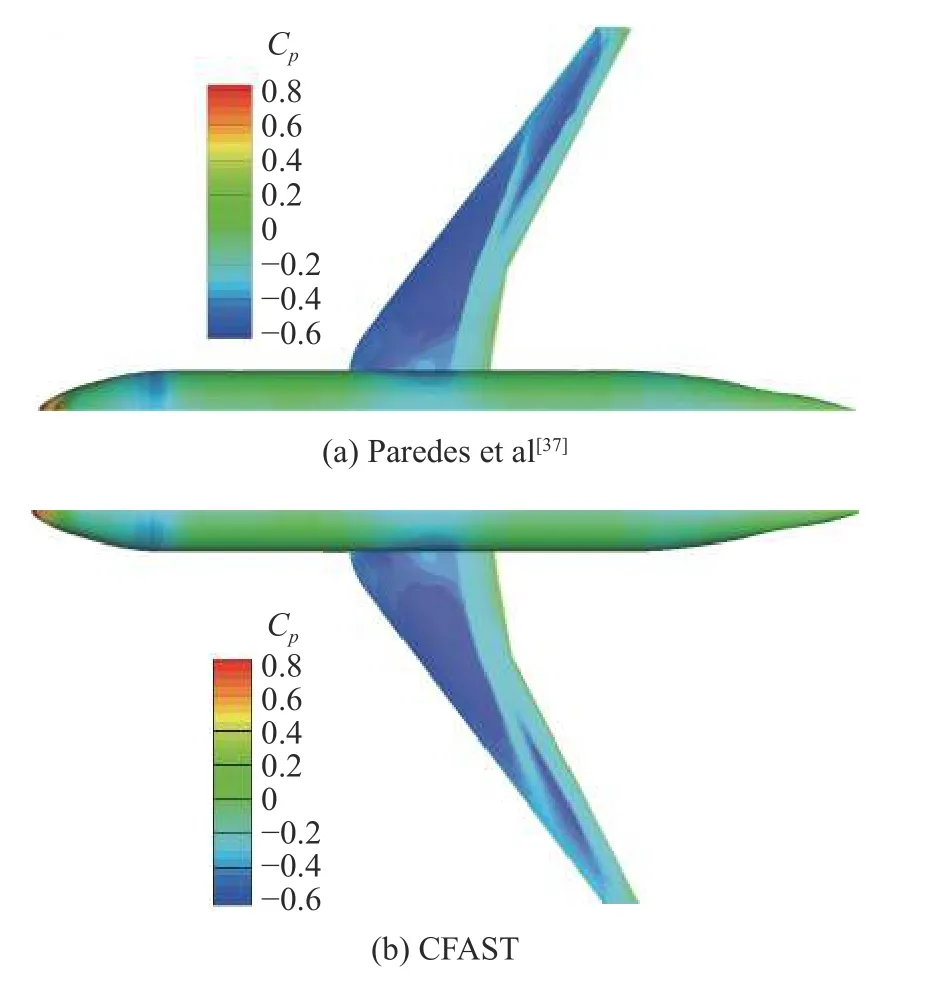
图9 带转捩计算的表面压力系数云图（Case 1）Fig.9 Contours of surface pressure coefficient in the imposed transition front solutions for Case 1

图10 进一步展示了不同翼展位置的表面压力系数Cp的弦向分布，并与NASA 的试验结果[33]和Paredes 等[37]的RANS 结果进行了对比。本文与Paredes等[37]基于RANS 的转捩计算结果基本重合，机翼激波位置较试验略有后移，机翼吸力面激波前压力整体略低于试验，其余与试验吻合较好。图11 展示了表面摩擦系数分布，对于摩擦系数突增的转捩点和摩擦系数陡降的激波位置，二者计算误差在5%弦长以内，说明CFAST 基本流计算结果准确可靠。需要指出，Paredes 等[37]的网格总数1.2 亿，本文网格总数110 万，单工况计算时间仅为200 s，CFAST 能准确捕捉基本流场的同时计算效率明显提高。

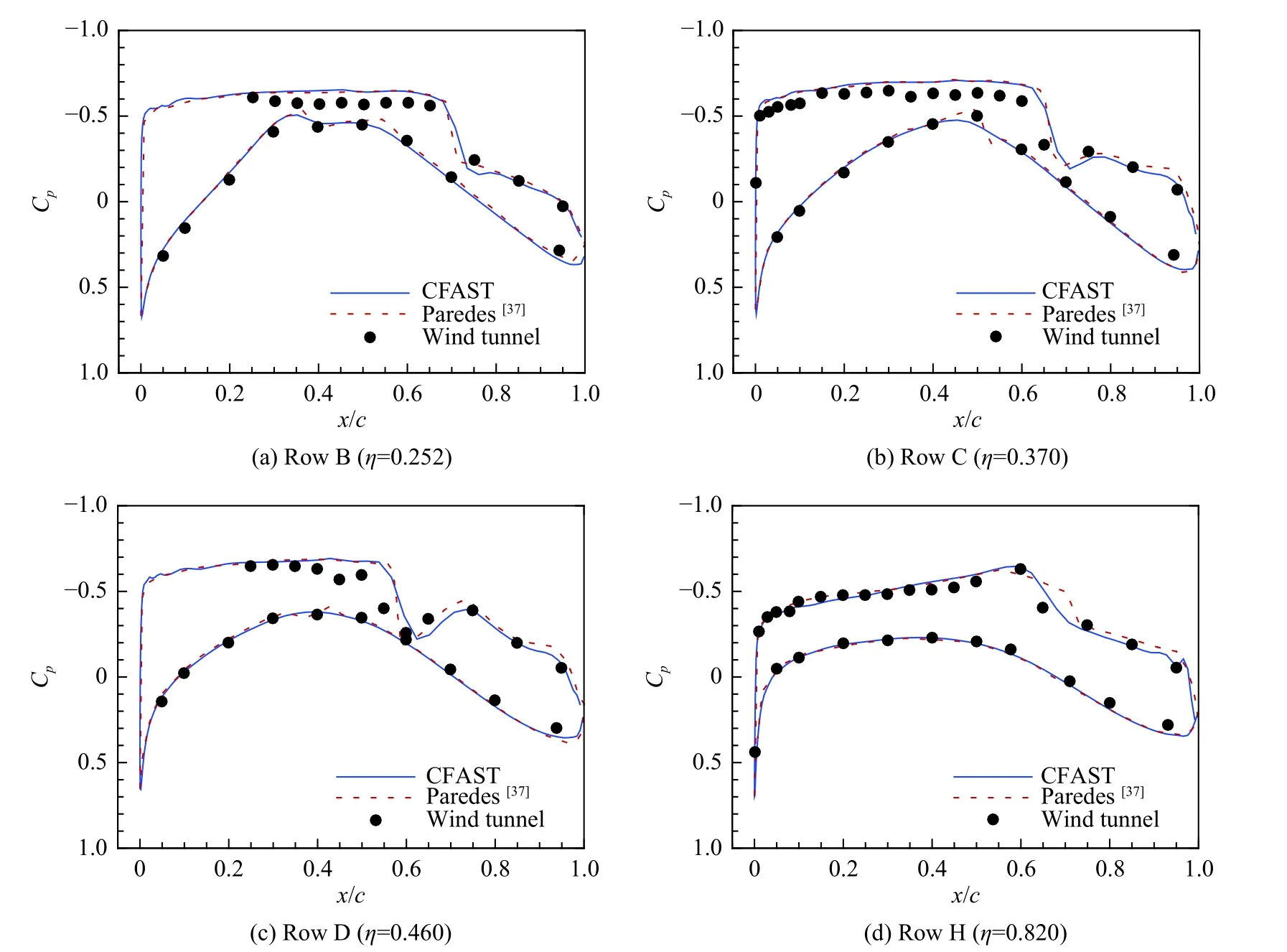
图10 不同翼展位置的表面压力系数（Case 1）Fig.10 Experimental and predicted pressure coefficients at different sections of the wing for Case 1

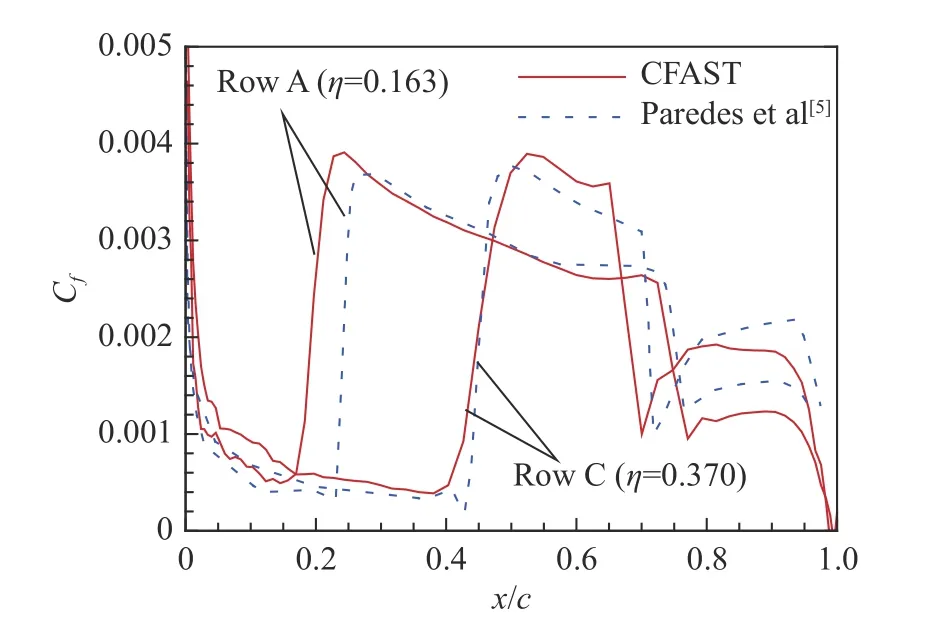
图11 表面摩擦系数分布（Case 3）Fig.11 Friction coefficient distributions at different sections of the wing for Case 3

3.2 转捩预测分析

标模CRM-NLF 转捩由横流驻波模态和T-S 模态主导。图12 展示了标模CRM-NLF 机翼上表面T-S波（红实线）和横流驻波（蓝实线）不稳定性扰动放大因子N增长曲线，图中黑实线表示风洞试验的转捩位置，黑点画线表示CFAST 计算获得的机翼上表面压力系数分布。由图可知，在展向37%处站位RowC（机翼拐折）以内，转捩由T-S 模态主导，站位I在接近激波附近的区域T-S 模态快速增长，可能是由激波诱导层流分离导致的。需要指出，T-S 模态和横流驻波模态的N均不超过7，说明标模CRM-NLF 机翼的压力分布通过机翼前缘抑制横流驻波模态和机翼中段抑制T-S 模态可以兼顾控制T-S 模态和横流驻波模态的增长幅度，使机翼表面维持较长的层流区。

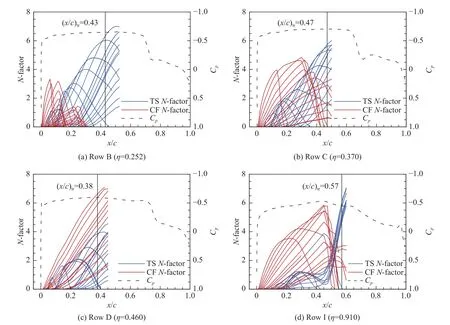
图12 不稳定模态沿流向的变化（Case 1）Fig.12 Streamwise variations of the N-factors of T-S and stationary crossflow modes for Case 1

eN方法是一种半经验的转捩预测方法，转捩N值可以根据试验转捩位置进行标定，也可以根据事先给定的转捩阈值 [(NTS)tr,(NCF)tr]，计算机翼的转捩位置，然后与试验结果进行比较。转捩由T-S 模态和横流驻波模态中先达到转捩阈值的不稳定模态主导。风洞试验来流湍流度为Tu=0.24%，根据Mack[38]的经验关系式N=-8.43-2.4ln(Tu)，转捩阈值为[(NTS)tr,(NCF)tr]=[6.0,6.0]。风洞试验研究了巡航马赫数下迎角和雷诺数对转捩的影响，本文在风洞试验的基础上还分析了马赫数对转捩的影响。

3.2.1 迎角对转捩的影响分析

图13 和图14 分别展示了迎角为1.5 和2.0 时扰动放大因子N的云图，并对比展示了Paredes 等[37]依据三维PSE 得出的计算结果，图中黑实线表示风洞试验测量得到的转捩线，黑虚线表示数值计算得出的激波线，实心圆表示转捩阈值[ (NTS)tr,(NCF)tr]为 [6.0,6.0]得出的转捩位置，与Lynde 等[34]和Paredes 等[37]进行转捩预测分析得出的转捩阈值一致。由图可知，本文计算得出的转捩位置和试验转捩位置基本一致。Lynde 等[34]和Paredes 等[37]分析风洞试验结果TSP照片认为机翼内段可能为T-S 不稳定模态诱发转捩。本文计算结果同样表明，机翼内段的转捩由T-S 不稳定模态主导。在机翼外段，横流驻波模态的N值明显较大，而此时转捩线与激波线基本保持一致，转捩可能是由激波导致的。对于T-S 模态，本文计算的N值与Paredes 等[37]计算结果基本保持一致，吻合很好；对于横流驻波模态，本文计算的N值在机翼中段整体略大于Paredes 等[37]的结果，而在机翼外段整体略小于Paredes 等[37]的结果，演化趋势一致，这可能是由PSE 考虑非平行性和机翼表面曲率导致的。随着迎角的增大，在翼展的大部分区域，横流驻波模态扰动放大因子N明显减小，转捩主要由T-S 模态主导。总之，本文基于CFD 快速分析工具CFAST进行线性稳定性分析能较为准确的进行转捩预测分析。

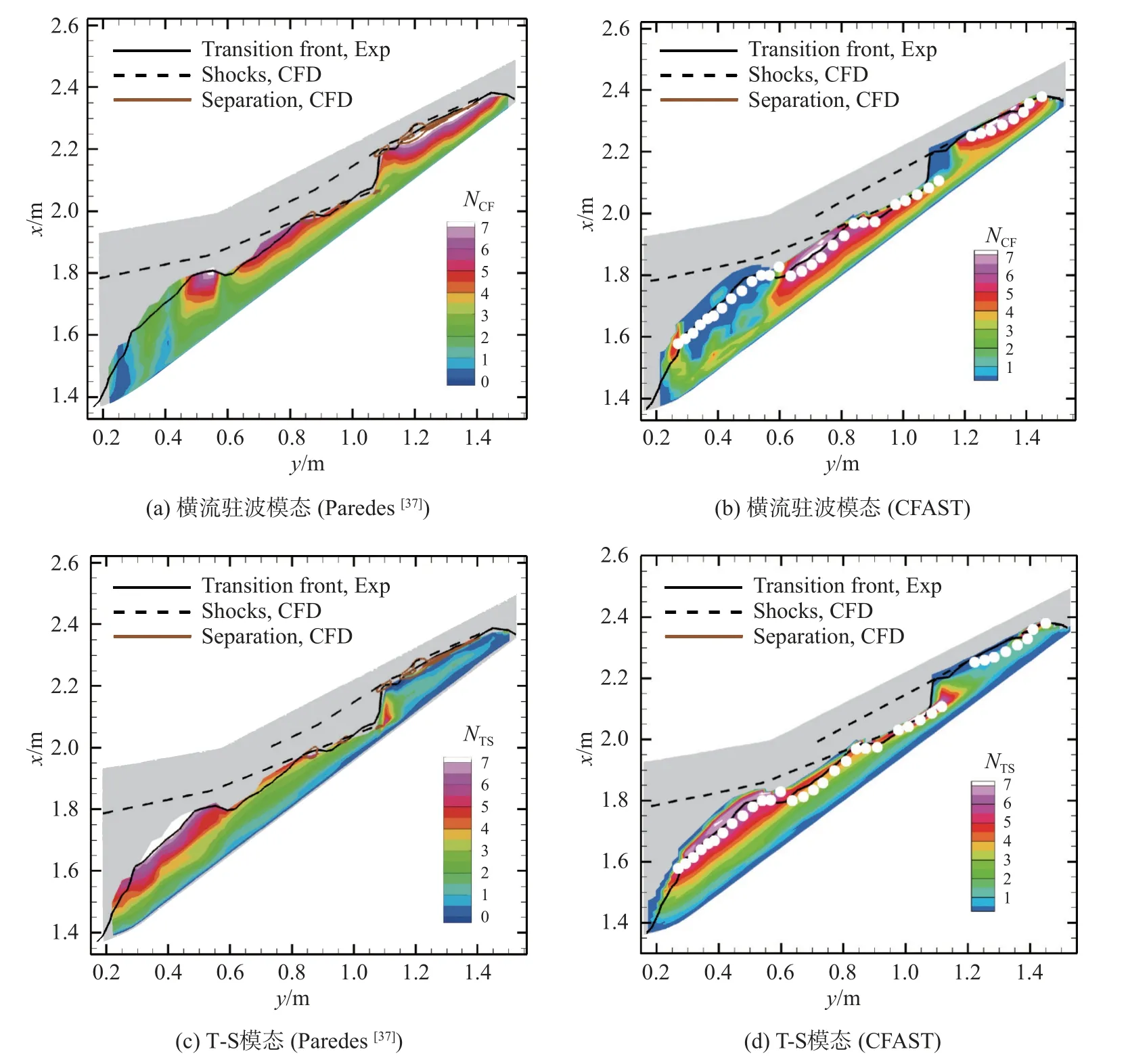
图13 横流驻波和T-S 波N 值的等值线云图（Case 1）Fig.13 N-factor contours of stationary CF waves and T-S waves for Case 1

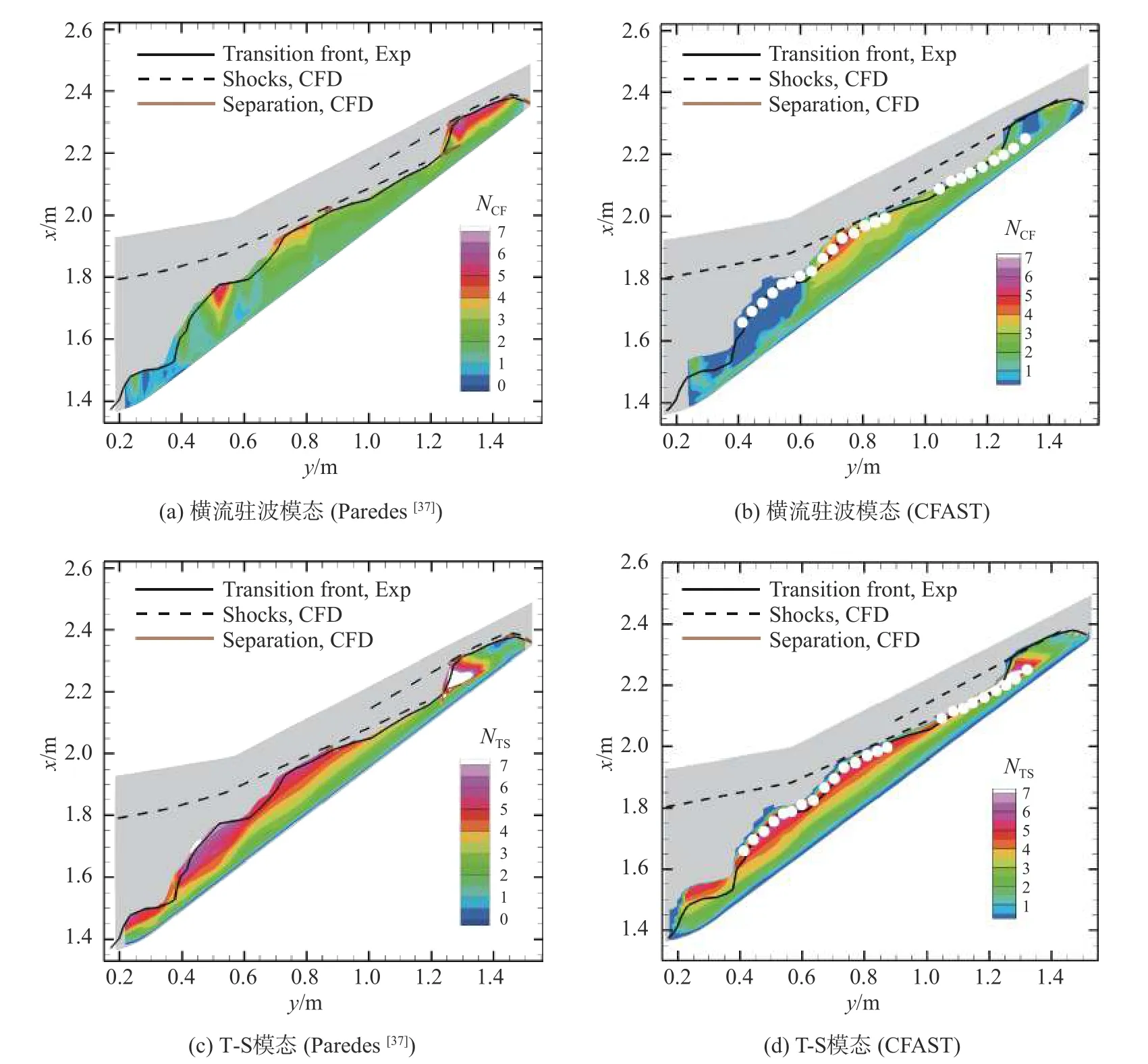
图14 横流驻波和T-S 波N 值的等值线云图 (Case 3)Fig.14 N-factor contours of stationary CF waves and T-S waves for Case 3

3.2.2 雷诺数对转捩的影响分析

图15 和图16 分别展示了雷诺数为12.5×106、15.0×106、17.5×106和20.0×106时横流驻波模态和T-S 模态扰动放大因子N的等值线云图，其他参数与表1 中的Case 1 一致。图中黑实线表示试验转捩位置，黑虚线表示激波线，实心圆表示转捩阈值[(NTS)tr,(NCF)tr]为 [6.0,6.0]得出的转捩位置。当雷诺数不超过17.5×106时，本文计算得出的转捩位置和试验转捩位置基本一致，雷诺数为20.0×106时，本文计算得出的转捩位置和试验转捩位置偏差增大。随雷诺数从12.5×106增大到15.0×106，转捩位置变化不明显，机翼内段的转捩由T-S 不稳定模态主导，机翼外段的转捩可能是由激波导致的；而随雷诺数继续增大到17.5×106和20.0×106，转捩位置明显前移，横流驻波模态N值明显增大，而转捩位置处的T-S 模态N值有所减小，机翼外段的转捩可能由横流驻波模态主导。造成风洞试验转捩位置前移的原因可能是：一方面随雷诺数增大，流动容易不稳定，转捩位置会前移；另一方面，边界层厚度随雷诺数的增大而变薄，风洞品质和机翼表面瑕疵等因素对转捩的影响会明显增强，当雷诺数增大到20.0×106时，可能在前缘直接诱发转捩。

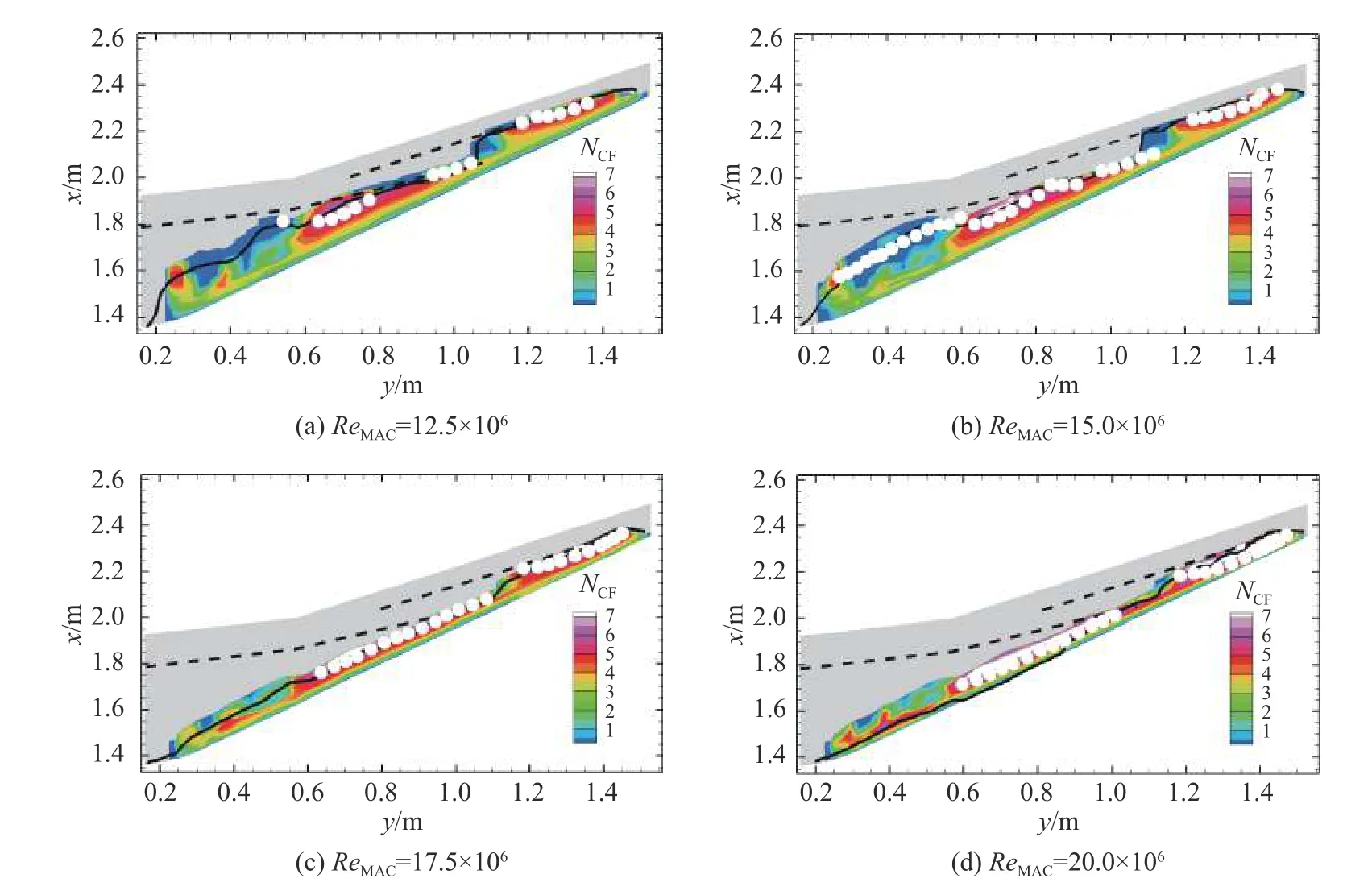
图15 横流驻波模态N 值云图Fig.15 N-factor contours of cross-flow modes at different ReMAC

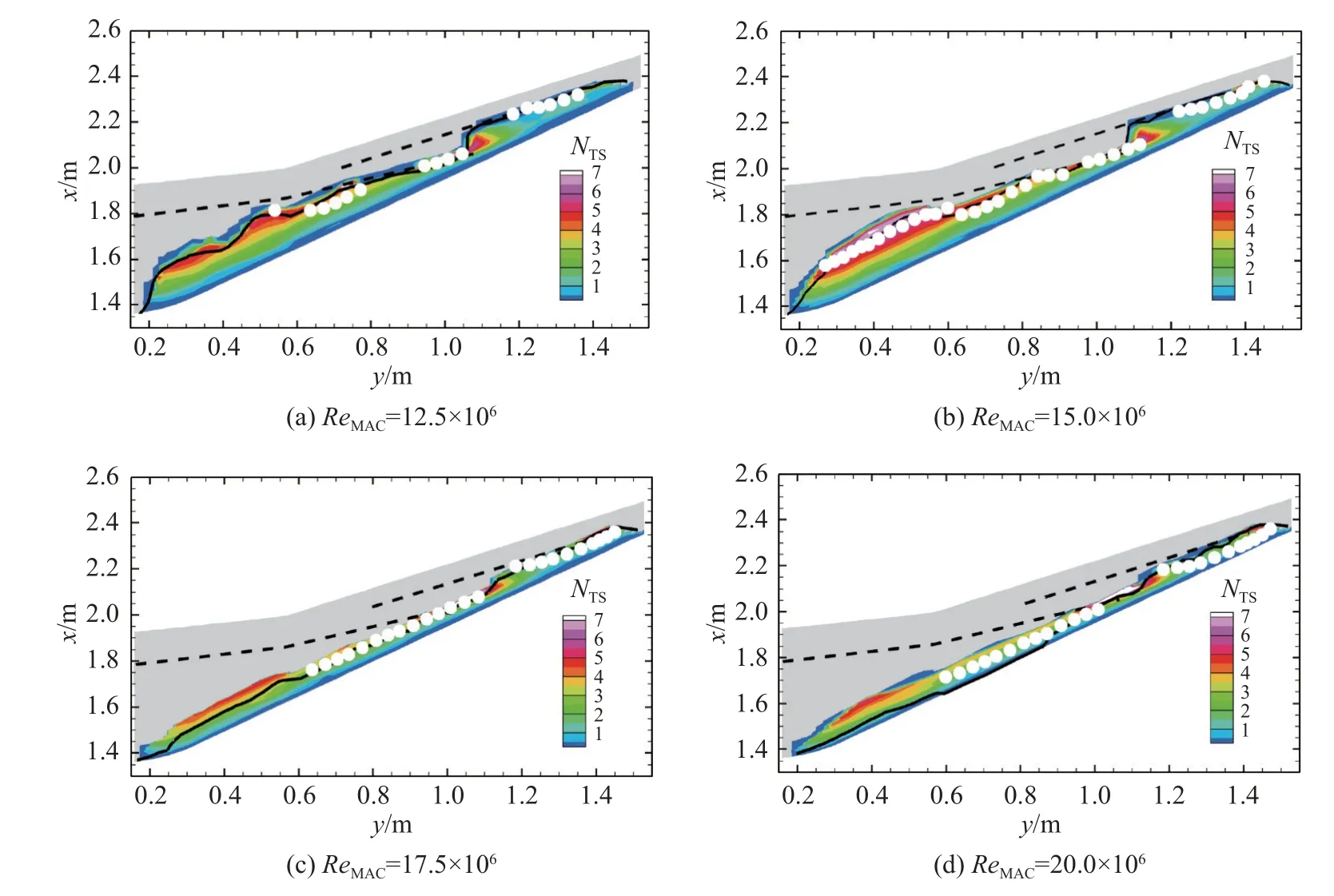
图16 T-S 模态N 值云图Fig.16 N-factor contours of T-S modes at different ReMAC

3.2.3 马赫数对转捩的影响分析

在风洞试验基础上，本节分析了马赫数对转捩的影响，其他参数与表1 中的Case 1 一致。图17 展示了不同马赫数时表面压力系数Cp分布。由图可知，随马赫数从0.856 降为0.820 和0.800，Cp分布变化明显，机翼中段由弱顺压梯度区变为逆压梯度区，激波消失。随马赫数从0.856 增加到0.870，激波位置后移，激波强度有所增强。图18 和图19 分别展示了横流驻波模态和T-S 模态扰动放大因子N值云图。与图13（Ma=0.856）相比，随马赫数增大，横流驻波模态N值逐渐增大，而T-S 模态N值明显减小。图中黑点划线表示 [(NTS)tr,(NCF)tr]=[6.0,6.0]作为转捩阈值得出的转捩位置。随马赫数增大，內翼段转捩位置明显后移，而外翼段层流区长度超过50%弦长，变化不明显。

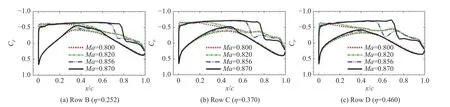
图17 不同翼展位置的表面压力系数Fig.17 Pressure coefficients at different sections of the wing

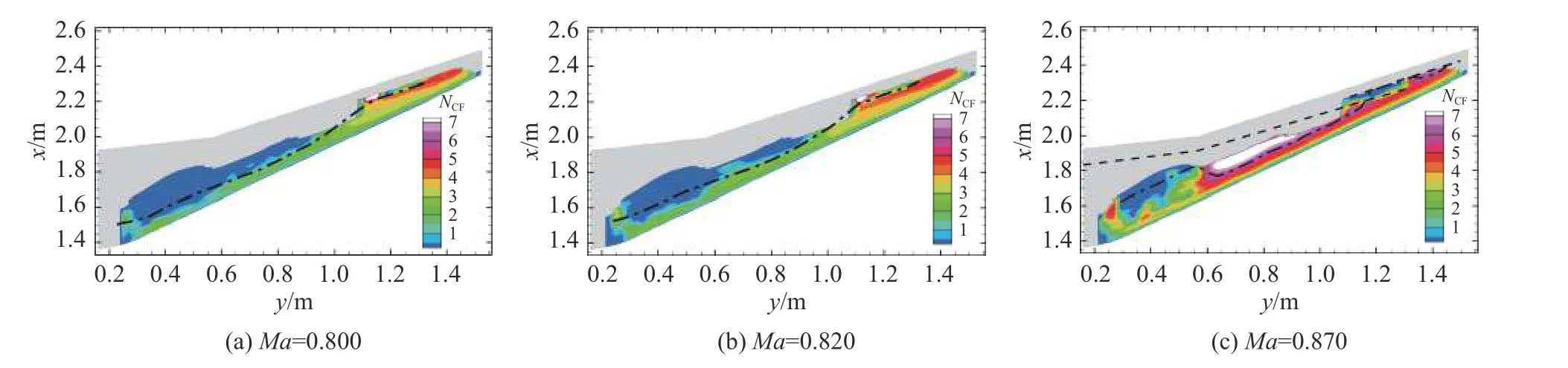
图18 横流驻波模态N 值云图Fig.18 N-factor contours of stationary cross-flow modes

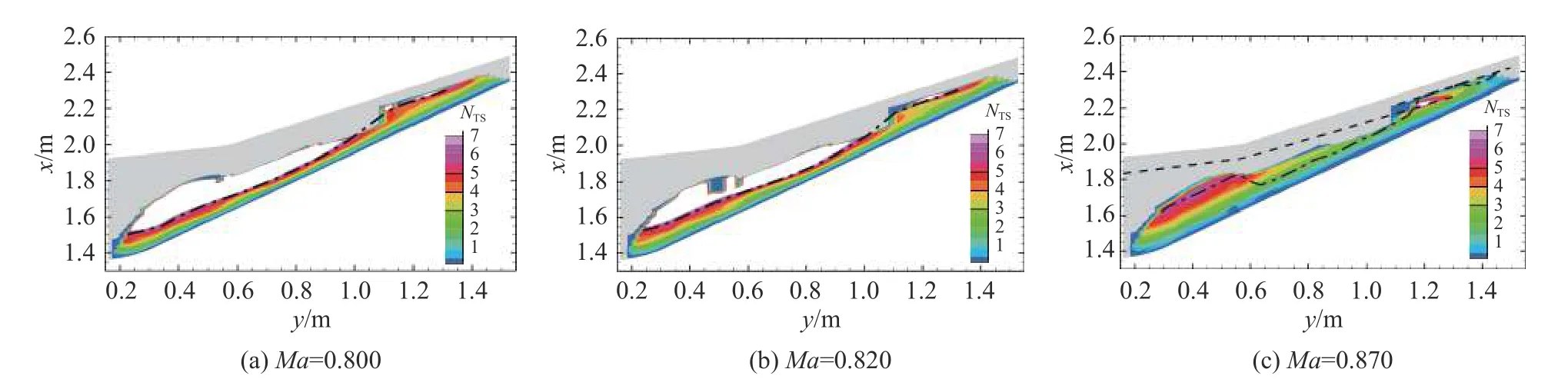
图19 T-S 模态N 值云图Fig.19 N-factor contours of T-S mode

4 结论

标模CRM-NLF 的后掠机翼边界层是典型的三维边界层，其转捩由横流驻波模态和T-S 模态主导。本文基于跨声速自然层流标模CRM-NLF 的风洞试验数据，结合内部快速CFD 分析工具CFAST 和eN转捩计算工具进行了转捩预测分析。总结如下：

1）通过转捩N值标定，研究发现，在内翼段，转捩由T-S 模态主导；在外翼段，转捩由横流驻波模态和激波共同主导。随着迎角和雷诺数的增大，转捩位置会有所前移。采用双eN方法，通过湍流度结合Mack公式确定T-S 模态和横流驻波模态的转捩N值为6，预测的转捩位置与风洞试验结果吻合很好，能较为准确的进行转捩预测分析；

2）在风洞试验的基础上本文分析了马赫数对转捩的影响。马赫数在0.800～0.870 之间时，随马赫数增大，內翼段的转捩位置明显后移，而外翼段层流区长度超过50%弦长，变化不明显；

本文旨在开发一套适用于复杂三维外形的快速转捩预测工具，经CRM-NLF 标模验证CFAST 在个人计算机上工况的基准分析时间约200s，且转捩预测精度足够，初步达成研究目标，在后续层流设计研究中，有助于加速后掠翼层流优化设计的迭代效率。后续也将进一步研究来流湍流度和表面制造因素对转捩的影响。