智能空气动力学若干研究进展及展望
唐志共,朱林阳,2,向星皓,2,何 磊,赵 暾,王岳青,钱炜祺,*,袁先旭,2,*
(1.中国空气动力研究与发展中心,绵阳 621000;2.空天飞行空气动力科学与技术全国重点实验室,绵阳 621000)
0 前言
空气动力学是研究飞行器或其他物体在同空气或其他气体作相对运动情况下的力/热特性、气体的流动规律和伴随发生的物理化学变化。它是在流体力学的基础上,随着航空工业和喷气推进技术的发展而成长起来的一个学科。现代空气动力学的相关研究活动大约可追溯到1903 年莱特兄弟试飞成功。与此同时,风洞技术也逐渐开始步入快速发展期。在随后的几十年中,风洞的种类和数量不断丰富,极大地推动了空气动力学的发展。20 世纪末,随着高速摄像技术的兴起,粒子图像测速仪(particle image velocimetry,PIV)被逐渐应用于流场测量,帮助研究者获得分辨率更高的流场。根据Jim gray 提出的科学研究的四大范式(图1),这种基于试验/实验的研究手段称之为第一范式。在19 世纪末20 世纪初,空气动力学从流体力学中分离出来成为一门独立的学科,研究者开展了与该学科更为紧密相关的理论分析,例如,升力定理、激波关系式等。基于演算分析的归纳总结研究称为第二范式。20 世纪70 年代,随着计算机软、硬件技术的快速发展,计算流体力学(Computational Fluid Dynamics,CFD)开始成为新的研究手段并广泛应用到空气动力学研究中。网格生成技术、数值格式、流场可视化技术等迅速发展。基于数值计算的研究范式称为第三范式。经过百余年的发展,空气动力学实现了从理论到应用等各个方面的巨大发展。然而,目前研究者仍面临诸多问题。例如,转捩的准确预测,大分离、非平衡湍流的准确计算,近壁区流场的准确测量,多源数据融合问题,以及湍流燃烧,气固界面作用等。根据当前的研究进展,这些困难与挑战是上述三种研究范式难以解决的。

图1 现代空气动力学研究范式Fig.1 Research paradigm of modern aerodynamics
2006 年,Hinton 提出了深度学习技术[1],随着第三次人工智能革命的兴起,人们实现了深度神经网络的训练和开发利用,数据驱动成为推动科学发展的第四范式。2012 年,谷歌的深度学习算法在ImageNet比赛中打败了传统的计算机视觉算法,推动了深度学习算法在图像识别方面的快速发展。2016 年,谷歌的AlphaGo 计算机在围棋比赛中击败世界冠军李世石,引起全球关注[2]。机器学习方法也在人脸识别、语音识别以及自动驾驶等众多领域广泛应用。近年来,研究者在数据驱动的基础上积极将科学知识与人工智能技术相融合,进而促进了“第四范式”的快速发展。Lu 等[3]提出DeepONet 算子学习方法,实现无限维函数空间之间的映射学习。华为公司通过对全球海量气象历史数据的学习,建立起了“盘古”气象大模型,预测精度超过传统数值方法,且速度提高了1 万倍以上[4]。孙浩教授团队与华为公司合作,基于昇思MindSpore AI 框架提出了物理编码递归卷积神经网络(physics-encoded recurrent convolutional neural network,PeRCNN),模型泛化性和抗噪性明显提升,长期推理精度提升了10 倍以上,在航空航天、船舶制造、气象预报等领域有广阔应用前景[5]。此外,机器学习也正在快速推动实验流体力学技术的发展[6]。在此背景下,空气动力学与智能化技术的紧密结合衍生了一门新兴交叉学科——智能空气动力学。由风洞试验、飞行试验和CFD 计算生成的海量数据为空气动力学的智能化相关研究提供了数据基础,现有的空气动力学理论提供了所需的物理知识约束,以及迅速崛起的人工智能技术提供了算法支撑,三者共同推动了智能空气动力学的快速发展。
1 内 涵
1.1 定义
智能空气动力学是指运用智能科学方法和研究范式研究空气运动,尤其是物体与空气相对运动时空气对物体所施作用力规律、气体的流动规律和伴随发生的物理学变化,解决空气动力学问题的新的交叉学科。在空气动力学三大传统研究手段的基础上,智能空气动力学引入第四研究范式(数据驱动),依托高性能计算、大数据、人工智能等技术,不仅实现传统空气动力学研究手段效率的有效提升,同时通过量变到质变,融合多源数据自主研究空气动力学规律,辅助科学发现,完善空气动力学理论体系,拓展理论边界;解决空气动力学基础理论、试验、评估与设计等方面问题,支撑飞行器气动技术“基础研究-设计研发-试验评估-工程应用”全链路能力提升与创新发展。
1.2 学科交叉
智能空气动力学涉及到空气动力学、数学、计算机科学、数据科学等多学科。首先,基于实验/试验、理论和计算三大经典研究范式积累的空气动力学现有知识体系是基础。一方面为智能空气动力学的发展提供了所必需的较为完备的物理约束和科学指导;另一方面,经典范式作为生成高可信度数据的手段为其提供了所依赖的数据基础。数学是智能技术发展的原动力。万能近似定理等理论证明,机器学习新方法、优化算法、参数初始化方法、批规范化等技术的开发和创新均离不开数学学科的严谨证明和推演。而智能化技术中算法的实现、函数库的建立以及算法在软硬件系统的集成等则需要计算机科学的支撑。数据科学本身就是一门涉及多学科交叉的学科,通过利用各种相关数据寻找解决问题的途径。针对空气动力学中复杂多样的研究需求,数据科学帮助研究者根据问题特性确定最佳数据驱动方法和智能化技术。
1.3 智能空气动力学研究范畴
相较于实验空气动力学、计算空气动力学,智能空气动力学的典型工程应用具有以下特征:一是通常是多研究手段和数据的综合应用,有效提高了效率、精度和适用性;二是通过“端到端”建模等方法,弥合了机理不清、算力不足等“技术鸿沟”,能够解决一些传统手段难以解决的气动问题;三是有效融入经验和知识,并能在解决实际工程问题的过程中通过强化学习等手段实现自学习与自动寻优。目前,智能空气动力学的应用领域主要包含以下4 个方面:一是湍流/转捩/燃烧/界面动力学等复杂力学现象预测与机理分析研究,主要是通过AI 来实现非定常、跨尺度等复杂流动现象的建模,发现或辨识控制方程以及开展量纲分析、标度律构建等研究;二是流动主动控制,智能的引入主要采用两种策略[7],一种是将流动控制问题转化为控制律的参数或控制律的函数形式的优化问题,再采用智能优化算法对优化问题进行求解,另一种策略是基于强化学习的主动控制;三是气动优化设计,人工智能(artificial intelligence,AI)可以辅助设计变量降维和气动特性与几何参数之间机器学习模型的构建,从而提高优化效率和优化结果精度;四是智能飞行,针对全阶段自主飞行、应急情况自动处置、复杂环境规避与利用等需求,智能空气动力学主要是在高精度气流感知、实时气动建模与智能控制、飞行器智能变体、气动约束下的编队优化与路径规划等方面发挥作用。除此之外,智能化方法在数值仿真和实验开展等方面也将起到有力的促进和推动作用。
2 研究方法
2.1 方法简介
基于算力、模型、算法和数据这4 个技术基础,智能空气动力学的研究方法是空气动力学三大传统研究手段与高性能计算、大数据、人工智能研究方法的结合,是涉及多学科的交叉综合研究方法,主要包括机器学习、数据挖掘、智能优化、数据融合方法等。
机器学习是指计算机模拟人类的学习行为,利用数据训练模型,然后使用模型进行预测的方法。与预先编写好、只能按照特定逻辑去执行指令的软件不同,机器实际上是通过“自我训练”学会如何完成一项任务。机器学习按学习策略可分为统计学习、符号学习和神经网络学习。深度学习是机器学习的子集,是对深度神经网络的构建和训练。根据万能近似定理,只要网络的隐层有足够多的神经元,它就可以以任意精度逼近L2(Rn)中的任意函数。在采用深度神经网络对非线性映射进行逼近时,网络的架构决定了逼近能力的上限。深度学习领域的主要网络架构的发展脉络如图2 所示。基本的深度神经网络是多层感知机(multilayer perceptron,MLP),通过误差反向传播算法进行网络权值的训练,与浅层网络相比,由于层数的增加,深度神经网络权值训练会遇到梯度消失、易于陷入局部极值等问题,因此深度神经网络采用ReLU、maxout 等激活函数代替sigmoid 函数,并对梯度优化算法进行改进,采用批量随机梯度下降法B-SGD、动量法、Adam 等方法,较好地克服了这些问题。近年来,卷积神经网络、循环神经网络(recurrent neural network,RNN)、长短期记忆网络(long shortterm memory,LSTM),生成对抗网络(generative adversarial network,GAN)、Transformer 等网络架构先后被提出并应用于不同的问题情境。
涪陵页岩气开发建设初期,正在海外开拓市场的张相权承担重任,被任命为试油138队队长,领导第一支进驻涪陵工区的试气队伍。

图2 深度学习主要网络架构Fig.2 Main network architectures of deep learning
得益于人工智能技术的兴起和海量流场数据的支撑,机器学习方法在旋涡提取问题中越来越受到关注,如基于三层BP 网络[130]、自适应增强(adaptive boosting,AdaBoost)法[131]和多数投票法[132]的旋涡识别技术。这些方法通过预先训练模型等方法有效减少假阳性和假阴性,但这些方法与流场的大小和形状有关,通用性较差,可扩展性不强。随着卷积神经网络(CNN)技术的突破,一些研究工作直接运用计算机视觉领域中成熟的CNN 网络模型来检测流场旋涡结构,如CNNBased[133]、EddyNet[134]、Fluid RCNN[135]、RNNVortexNet[136]等。由于CNN 可以有效地抵抗平移、变形、缩放和旋转等识别困难,基于CNN 的旋涡提取模型能在类似的其他流场中取得较好的性能,一定程度上解决了通用性较差的问题。Ströfer 等[135]提出了一种基于RCNN 的流场特征识别方法。通过流场特征标签数据集训练该网络模型,在二维回流区域、二维边界层和三维马蹄形旋涡的识别上得到了成功的应用。这种数据驱动的流场特征识别方法为多种不同流场特征提供了一种通用的识别方法,利用CNN 网络强大的非线性映射能力,无须进行复杂且显式的物理控制方程的计算,且能够很好地快速检测出流场中未知特征结构。但是,该方法的计算复杂度很高,因为它需要计算流场中每个网格点的十个伽利略不变的衍生变量,并将其作为网络模型的输入。Liu 等[137]提出了DEDNet,一种基于高频雷达数据像素分割框架的近海旋涡检了基于不同的深度学习模型(CNN、Resnet 和Unet)的旋涡边界识别方法。具体来说,首先通过一个参数化流动模型生成大量的旋涡标签数据,之后使用小块速度场数据训练不同网络模型,最后推广至二维真实的公开模拟数据集Cylinder[138-139]。实验结果表明,这些网络模型可扩展性较强,具有阈值无关性,并都能较好地识别出旋涡边界,且UNet 网络模型性能表现最佳。基于局部Q准则标记的旋涡样本数据集,Kashir 等[140]提出了一种面向网格单元的全卷积对称旋涡提取网络。该模型采用速度场和涡量场作为输入,研究了网络结构中卷积和反卷积块数量对提取精度的影响,以获取最高的精度,同时避免模型退化问题,并成功应用于不同速度边界值和雷诺数的二维方腔流场数据。该方法的实验数据是笛卡尔网格流场数据,本质上与图像数据类似,从而可以直接运用计算机视觉领域中的深度学习模型,并取得较好的精度。然而,未考虑常用的不规则结构网格或非结构网格二维和三维流场数据,该方法的应用范围有限。Abras 等[141]基于卷积神经网络,设计了一种流动物理特征识别的智能化方法,并在悬停旋翼尾迹涡识别与破裂分析中得到成功的应用。该方法通过将三维流场体数据转换成二维图像数据,从而可以直接迁移图像领域中的成熟模型。但是,这种处理方式会造成大量流场信息的丢失,同时未考虑流场数据本身的特性,该模型的泛化能力较弱,仅仅适用于某些特定流动状态的旋涡分析。Li 等[51]基于XGBoost[142]实现了圆柱绕流中的湍流区域识别。该方法不仅与阈值无关,且能融合多个流场属性变量,有利于发现湍流中多尺度的物理过程。但是,多个流场属性变量中可能存在冗余,同时该方法是逐点进行识别的,大大增加了计算成本。Fan 等[143]设计了SymmetricNet 网络,使用海面高度、海面温度和流动速度等融合多变量信息的特征作为该网络的输入,海洋中尺度旋涡识别精度达97.06%。Ye 等[144]使用一种基于分割卷积网络的旋涡识别方法,提高了旋涡识别效率和精度。Luo 等[145]采用一种基于YOLOv3 网络[146]的叶尖旋涡检测方法,较快且准确地识别出流场旋涡结构。这三项研究都是将流场数据像素化后,直接迁移相关成熟的目标检测模型进行旋涡提取,未考虑复杂流场数据的本身特性,普适性较差。上述方法存在两个主要问题:第一,大多方法将流场直接转化为图形图像处理,丢失网格拓扑信息;第二,仅能处理单块网格或者规则网格,无法处理多块网格和不规则网格的流场。这两个问题影响了流场特征智能提取的精度和应用场景。
智能优化算法是通过模拟揭示某些自然现象或过程发展而来的优化算法,具有全局、并行、高效的优化性能,鲁棒性和通用性强,为解决大规模非线性问题提供了新的思路和手段。智能优化算法不仅在气动优化设计领域得到广泛应用,近年来还逐步扩展到非线性气动微分方程求解等领域。但在实际应用中也存在以下问题:一是算法的理论性有待完善,用传统优化算法求解优化问题拥有完善的理论依据,而智能优化算法的理论研究一直滞后于它的应用,如何证明智能算法解的存在性、收敛性还需要进一步深入研究。二是算法普遍存在早熟收敛,易陷入局部最优,收敛速度慢的问题,其核心是如何有效平衡算法局部搜索和全局探索能力的问题。对于算法理论性不足的问题,研究者主要从马尔可夫链模型和统计力学逼近模型等角度对算法的收敛性开展研究[20]。对于早熟易陷入局部最优问题,则一是采用多种群协同进化策略,增加样本的多样性,提升发现全局最优的能力;二是设计新型搜索策略,如采用Lévy 策略协助算法跳出局部最优;以及在搜索过程中不将适应值作为唯一标准,而是将搜索结果进行分类,类与类之间通过设定的规则进行信息的交换,可较好地兼顾局部和全局搜索能力;三是对进化策略进行改进完善,将动物和人类的一些生物特性思想引入传统群智能算法,如人口种群自适应和人体自身免疫机制、狼群算法中引入游走行为、召唤行为和围攻行为,分别提升算法的搜索能力、收敛性和局部寻优能力[21]。
从图中可以看到,低可信度数据中的噪声对融合结果影响不大(图25(a)),当高可信度数据较少(9 个点)时,高可信度数据中的噪声会对融合结果造成较大影响(图25(b));而当高可信度数据量较大(101 个点)时,噪声的影响反而下降(图25(c))。这是由于深度网络会优先学习数据中的低频部分。具体来说,当训练数据量较少时,原始数据和噪声数据具有相似的频率,这导致融合网络将两者特征一并学习;而当训练数据量较大时,原始数据和噪声数据可以明显得分为低频和高频部分,从而根据深度学习的频率原则,所构建的融合网络会优先学习低频原始数据,使其预测输出具有更强的鲁棒性。
(2) 内侧仿形阴极板的形状与导流装置横截面的形状相似,且材质完全相同,避免了出现尖端效应,消除了内腔氧化膜厚度不均、电解着色存在色差等缺陷。

表1 智能空气动力学研究方法与传统手段研究方法的主要差异Table 1 Main difference of research methods between artificial and classical aerodynamics
2.2 基本流程
空气动力学问题的智能化求解过程包含多个环节。首先是获取并处理数据。一般而言,研究者需要根据研究问题收集已有的数据或者生成新的数据。数据空间在本质上决定了模型所能学习到的内容,因而也间接地影响模型最终性能。模型性能不及预期的原因之一可能是数据量不足导致的。数据处理包含标准化/归一化、样本选择以及特征构建/选择等诸多环节。标准化/归一化一般是为了避免不同输入特征之间的数值量级差异,保证数据不失一般性。样本选择的主要目的一是为了简化数据集,提高训练效率;二是为了实现样本均衡,避免局部样本稀少或缺失造成的模型性能失衡。例如,简单构型的直接数值模拟(direct numerical simulation,DNS)算例在某一时刻的二维切片数据就可达十万量级以上,庞大的数据集造成的训练困难迫使研究者进行样本选择;对于实验而言,由于测量手段或技术的局限性,局部流场很难获得测量数据,容易出现样本不均衡的问题,一般可通过上采样或下采样等方法缓解。输入特征对模型性能的影响十分关键,特征构建相当于确定与模型输出相关的自变量,而特征选择的目的就是选出相关有用的特征进而提高模型性能。特征构建和选择过程一般依靠研究者自身的物理直觉确定,同时也需考虑满足不变量特性等约束。此外,该过程也可通过特定的算法进一步完善。
然后是确定并训练智能化模型。智能化模型的构建可基于具体的研究问题选择神经网络、随机森林、符号回归以及强化学习等架构甚至不同架构的组合形式。模型架构的复杂度可通过模型参数调节,例如神经网络的深度和宽度。在数据集和采用的模型架构确定后,按一定比例将数据集划分为训练集/验证集并导入模型开展训练。模型训练过程主要包含损失函数的定义,参数初始化方法和优化算法的选择等环节。此外,交叉验证有助于研究者选择最佳模型,避免过拟合问题。
最后是模型后处理。实际工程应用中,往往需要对模型预测的输出进行一定的后处理,避免出现非物理解,例如雷诺应力的可实现约束、涡黏非负、量纲一致性等约束。当预测样本相对训练样本外插较大时,容易因为位于模型性能边际或之外而导致异值的出现,可设置阈值予以剔除或限制。此外,通过概率分析还可以对模型预测结果进行不确定度分析,帮助研究者更好地评估结果的可信度。
3 智能空气动力学若干研究进展
近些年经过国内外专家学者的努力,目前智能空气动力学已在研究方法、流场预测、模型构建等诸多方面取得相当进展。就国外而言,科罗拉多大学Raissi 团队在物理嵌入的神经网络(physics-informed neural networks,PINNs)方法、普林斯顿大学Brunton团队在AI 与CFD 的交叉领域、斯图加特大学肖恒团队在湍流建模方面以及其他团队在诸多领域均开展了开拓性的研究。与此同时,国内专家也开展了丰富的研究工作,例如北京大学鄂维南、香港科技大学徐辉等研究团队开展了机器学习理论和方法研究;西北工业大学张伟伟、中科院力学所杨晓雷、南方科技大学王建春、清华大学张宇飞、浙江大学夏振华等研究团队开展了湍流模型构建及数据处理等研究;上海交通大学刘应征等团队开展了数据驱动与实验的融合研究;华为公司联合中国商飞和西北工业大学开发了面向大型客机翼型流场预测和设计优化的AI 大模型;其他更多相关工作可参见文献[23-26]。本团队结合自身研究基础,主要开展了流场预测、转捩/湍流建模、数据融合、气动力/热建模以及流场信息提取等方面研究工作。
3.1 流场预测
流场仿真是飞行器设计领域十分重要且耗时的一个环节,如何高效准确地获取机翼或者翼型的流场信息成为一个重要的研究课题。深度学习方法作为高维空间中一种高效的函数逼近技术,能够从大数据中自动寻找隐藏特征信息,并且可以直接处理原始形态数据获得经验或知识,从而可以预测复杂非线性系统的未来行为,为求解复杂耗时的N-S 方程提供了一种快速的可替代的解决方案。采用机器学习的代理模型可以减少试验成本、CFD 计算的内存消耗以及时间成本。通过从大量积累的流场数据中进行学习,至少在翼型设计初始阶段,可以使用机器学习方法减少CFD 模型的大量重复计算工作。利用人工智能技术对流场信息进行快速预测目前仍然处于探索阶段,但也取得了一定的研究进展。从深度学习模型的角度出发,主要分为如下几种研究方法。
第四个领域是数据驱动的线性稳定性预测方法。eN方法是基于线性稳定性理论的一种转捩预测方法,基本理念是边界层内各种频率和空间波数的扰动波进入不稳定区域后,以扰动波幅值放大倍数的N值曲线分布判断转捩[61]。人工智能研究则主要通过采用神经网络等智能算法对N值进行预测从而判断转捩位置。AI 在eN方法的首次应用是Crouch等[62]使用流场标量参数和层流速度剖面作为神经网络输入来预测最大不稳定性增长率,如图13 所示。近期研究主要有Zafar 和肖恒等[63-64]利用卷积神经网络和循环神经网络,以层流边界层轮廓特征和其他标量特征为输入,实现对二维翼型绕流不稳定放大因子N以及转捩位置的预测,如图14 所示。综合预测误差小于0.7%,预测效率比LST 提升了3~4 个量级,同时方法展现出强大的适用性。

图3 基于U-Net 深度神经网络的流场预测模型[27]Fig.3 Flow field prediction model based on U-Net deep neural network[27]
2)基于生成式对抗网络的流场预测。在流场预测研究中还有一类使用较多的深度神经网络模型是生成式对抗网络[40]。该网络模型一般包括一个生成器与判别器,通过博弈的方式来对深度神经网络模型进行训练,从而得到预测效果较好的生成器模型。Wu 等[41]基于GANs 提出了ffsGAN 网络框架,构建了参数化的超临界翼型与翼型流场之间的一对一映射关系。后又提出了基于预训练模型与微调模型的条件生成式对抗网络用于流场的预测任务[42],其中预训练模型利用条件生成对抗网络对训练数据的分布进行初步估计;其次微调模型采用两个生成器,其中一个生成器用于数据增强。这类生成式模型本质上讲在拟合流场数据分布时依然是将流场输入信息当做像素值进行处理,缺乏较强的物理约束,从结果上来看,通过该方法得到的流场数据特别是气动力参数曲线存在严重的不光滑性。因此关于该方法对流场预测的有效性仍需要做进一步的探索。
3)基于点云的流场预测。为了利用神经网络替代CFD 求解器获取流场信息,有效的数据表达是关键。对于广泛使用的卷积神经网络而言,其将均匀笛卡尔网格中的每个顶点当做一个像素值进行处理,但是在真实世界中存在复杂的几何构型,该方法对非结构化的网格数据是无效的。针对该问题,Ali 等[43]发展了一种基于点云网络架构的深度学习模型用于非结构化流场的预测。该方法将CFD 的求解域表示为一个点云,构建了每个点的坐标值与速度值以及压力值之间的映射关系。点云网络学习空间位置与物理参数之间的端到端的映射关系,继承了非结构化网络的良好特性,减小了网络的训练成本,保证了边界的光滑性以及数据的准确性。但是Ali 等仅对较为稀疏的网格流场进行了测试,并且从结果来看,在面对不同迎角的点云流场数据时,其预测结果与真实值之间存在较大误差。点云模型的构建策略依然是沿用了生成式模型的思想,深度学习模型映射关系的构造较为简单,不具有很强的物理约束效应,导致在面对不同工况下的流场预测问题时其泛化性存在很大问题。
4)基于图神经网络的流场预测。类似点云的数据表达手段,图神经网络在面对非结构的数据时存在先天的优势,如社交网络、交通网络、非结构化的流场等。图神经网络由部分节点以及连接不同节点的邻接矩阵组成,在图神经网络训练过程中,通过邻居聚合的方式来更新不同节点的数值。由N-S 偏微分方程描述的非定常流动具有高度非线性以及多尺度特性,特别是具有流动分离、涡脱落、剪切层等特征的流动现象表现出复杂的时空特性[44]。Pfaff 等[45]利用图神经网络对复杂物理仿真系统进行了模拟,实验结果展示了该方法与卷积神经网络相比能够有效捕捉近壁区的流场信息,且针对不同复杂工况以及几何的流场都能实现较为精确的流场仿真效果。Li 等[46]提出了一种对偶图神经网络用于发动机叶片的流场预测,所提出的方法不仅能够准确地预测叶片的性能参数,同时在流场重建中也具有出色的性能。该方法与上述其他方法而言,在构建深度学习模型训练数据时就考虑到了网格点的邻居信息以及当前节点与邻接节点之间的联结关系,摒弃了端到端建模以及像素化建模有效信息不足的缺点,极大提升了建模精度。
综合而言研究人员利用各类神经网络去预测不同几何的流场信息,但是目前的研究工作大多是对神经网络用于流场预测的有效性进行了验证。特别是在构建神经网络的输入以及输出的映射时,大多是采用将符号距离场函数以及迎角、马赫数等状态信息作为网络的输入去映射待预测的速度场以及压力场,而针对几何外形特征提取问题的研究较少。本团队使用在计算机视觉领域广泛应用的Transformer 网络架构替换了传统的CNN 网络架构去提取翼型的几何参数,并进一步建立了几何参数、雷诺数、迎角、流场坐标、壁面距离与翼型速度场以及压力场之间的映射关系[47]。训练得到的深度网络模型能够在一定程度上实现对不同雷诺数、迎角以及几何外形的泛化能力,且流场的预测速度与CFD 的计算速度相比提升了27 倍。总体网络架构如图4 所示。为了有效表征不同翼型的几何特征,首先将输入网络的翼型灰度图像做了切片处理并嵌入相应的位置信息;其次,将融合位置信息的翼型几何向量输入到Transformer 编码器中去提取翼型的几何注意力表达特征;最后,将Transformer 编码器提取的翼型几何特征与雷诺数、迎角、流场坐标以及壁面距离等进行融合后输入到深度学习模型去预测翼型的速度场和压力场。

图4 基于Transformer 网络架构的几何编码与流场预测网络模型Fig.4 Overall network architecture of airfoil geometry encoder and flow field prediction based on Transformer
将训练得到的深度学习模型用于对翼型测试数据集中的RAE2822 翼型(雷诺数:2 500,迎角:3°)流场进行预测。如图5 所示,训练得到的深度神经网络能够获得与CFD 相似的流场仿真结果,预测值与真实值之间的最小绝对误差为0.2%,最大绝对误差仅为4%。从图6 中可以发现,网络的预测值与真实值之间的相关性系数约为99.9%,说明深度学习模型能够准确捕捉翼型流场信息。

图5 RAE2822 翼型流场预测结果云图[47]Fig.5 Contours of the predicted RAE2822 airfoil flow field[47]
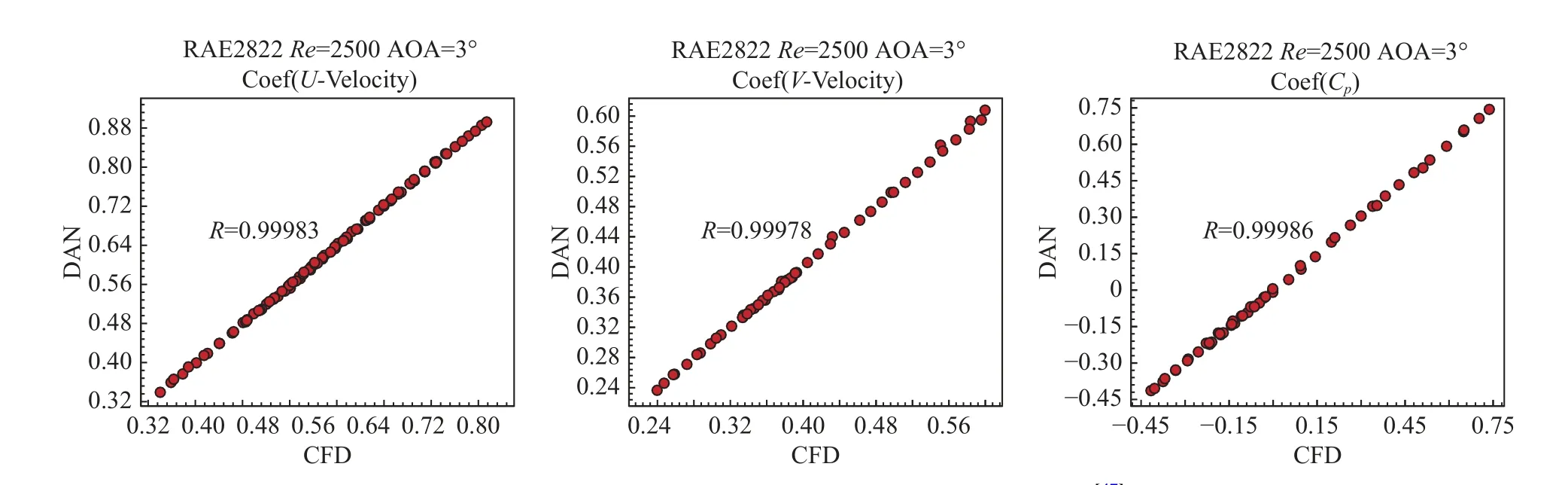
图6 翼型气动参数的预测值与真实值之间的相关性曲线[47]Fig.6 Correlation coefficients between the real and predicted variables in the RAE2822 flow field under Re=2 500,AOA=3° [47]
3.2 转捩建模
边界层转捩通常是指边界层流动由层流状态发展为湍流状态的过程,是一个多因素耦合影响的强非线性复杂流动物理现象[48]。根据美国国家高超声速基础研究计划(national hypersonic fundamental research program,NHFRP),边界层转捩是该计划的重要基础研究内容[49],而基于雷诺平均模拟的转捩模型是实现飞行器全机基于物理现象(非校准)转捩预测最为有效的方法。近年来,随着算法、算力的发展以及转捩数据的积累,机器学习方法在边界层转捩建模领域的研究正获得越来越多的关注。机器学习转捩研究通过人工智能方法建立或完善流体力学理论、模型和方法,推动流体力学的智能化应用,以弥补研究者对理论基础和经验的不足。将机器学习应用于转捩建模的最终目的是实现机器学习算法下的转捩模式特征的识别与转捩流场的模拟[50]。即通过对转捩相关的各种来流信息、流场当地信息以及转捩判据等作为输入,进行人工智能处理和分析,以期对转捩现象进行预测模拟、模态辨识乃至于机理分析。转捩建模的机器学习方法可参照其预测对象与应用目的进行划分,如图7 所示。数据驱动的机器学习转捩模型研究,大致可以划分为以下4 个研究领域:一是转捩判据与转捩智能识别;二是对基于雷诺平均的Navier-Stokes(Reynolds-averaged Navier-Stokes,RANS)方程的经典转捩模型的改善;三是数据驱动的转捩替代模型;四是基于人工智能的稳定性预测方法。

图7 人工智能转捩研究分类Fig.7 Research classification of transition with artificial intelligence
第一个研究领域主要是采用机器学习方法基于已有流场数据识别、判定层/湍流交界面,或针对未知流场预测转捩位置。Li 等[51]基于机器学习XGBoost 分类算法建立了不需要设置临界判据的DNS、大涡模拟(large eddy simulation,LES)流场层/湍流界面识别方法,实现了圆柱绕流层/湍流交界面的精确判定,如图8 所示。李昌林等[52]基于类似方法建立了针对发动机叶型绕流大涡模拟的转捩位置智能识别方法。在转捩位置的智能预判领域,孟德颖等[53]采用单层神经网络,基于风洞实测数据,实现了变迎角变雷诺数的高超声速转捩位置的全周向角辨识与判别,如图9 所示。该领域研究旨在对传统的基于实验数据的经验型转捩判据进行替代,能够在复杂的流场信息当中快速高效地进行转捩位置的识别与判定。
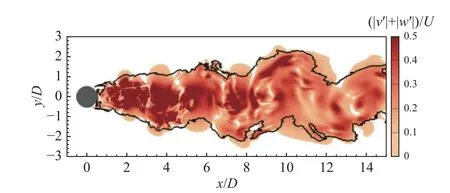
图8 Re=3 900 圆柱绕流脉动强度云图及智能识别层/湍流分界面[51]Fig.8 Fluctuation intensity of a Re=3 900 cylinder flow and the AI detected laminar/turbulence interface[51]

图9 单层神经网络示意图及高超声速尖锥周向转捩位置预测[53]Fig.9 Sketch of the neural network (NN) and the predicted transition front for a hypersonic sharp cone[53]
第二个领域研究较为广泛,主要是采用人工智能研究方法,针对现有模型的局限与不足,着眼于雷诺平均模拟的经典转捩模型预测性能的改善与提升:通过特定的实验数据和高精度数值计算结果进行训练,并对模型控制方程进行系数修正或源项修正,以期提升模型对于一定工况下的预测精度或拓宽模型适用范围。例如,杨沐臣等[54]针对不同迎角翼型的转捩流动,使用正则集合卡尔曼滤波获得k-ω-γ-Ar 模型时间尺度修正项后验分布,并建立从流场平均量到修正项的智能映射关系,实现了转捩模型对翼型预测性能的提升,如图10 所示;Duraisamy 等[55]基于γ一方程转捩模型,利用神经网络和高斯过程重构了γ 输运方程源项,改善了模型对于T3 系列平板的预测精度,如图11 所示。张天鑫等[56]基于流场反演和机器学习方法拓展了原始γ-Reθ转捩模型对高超声速边界层转捩的预测能力,采用卡尔曼滤波及随机森林方法完成了模型启动项及参数修正,并在变雷诺数、来流温度及钝度的钝锥算例中进行了充分验证。在符号主义的智能建模方面,赵耀民等[57]对基因表达式编程的湍流智能建模进行了详细全面的整理归纳,亦提及Akolekar 等[58]在转捩建模中的工作,对层流动能转捩模型中的层流黏性系数进行了修正,实现了叶栅分离诱导转捩的准确模拟。上述智能转捩研究仍以数据驱动为主,即采用修正目标的典型工况数据为驱动,对转捩模型控制方程的源项或系数进行智能修正或重构,与经典模型的修正方法类似。
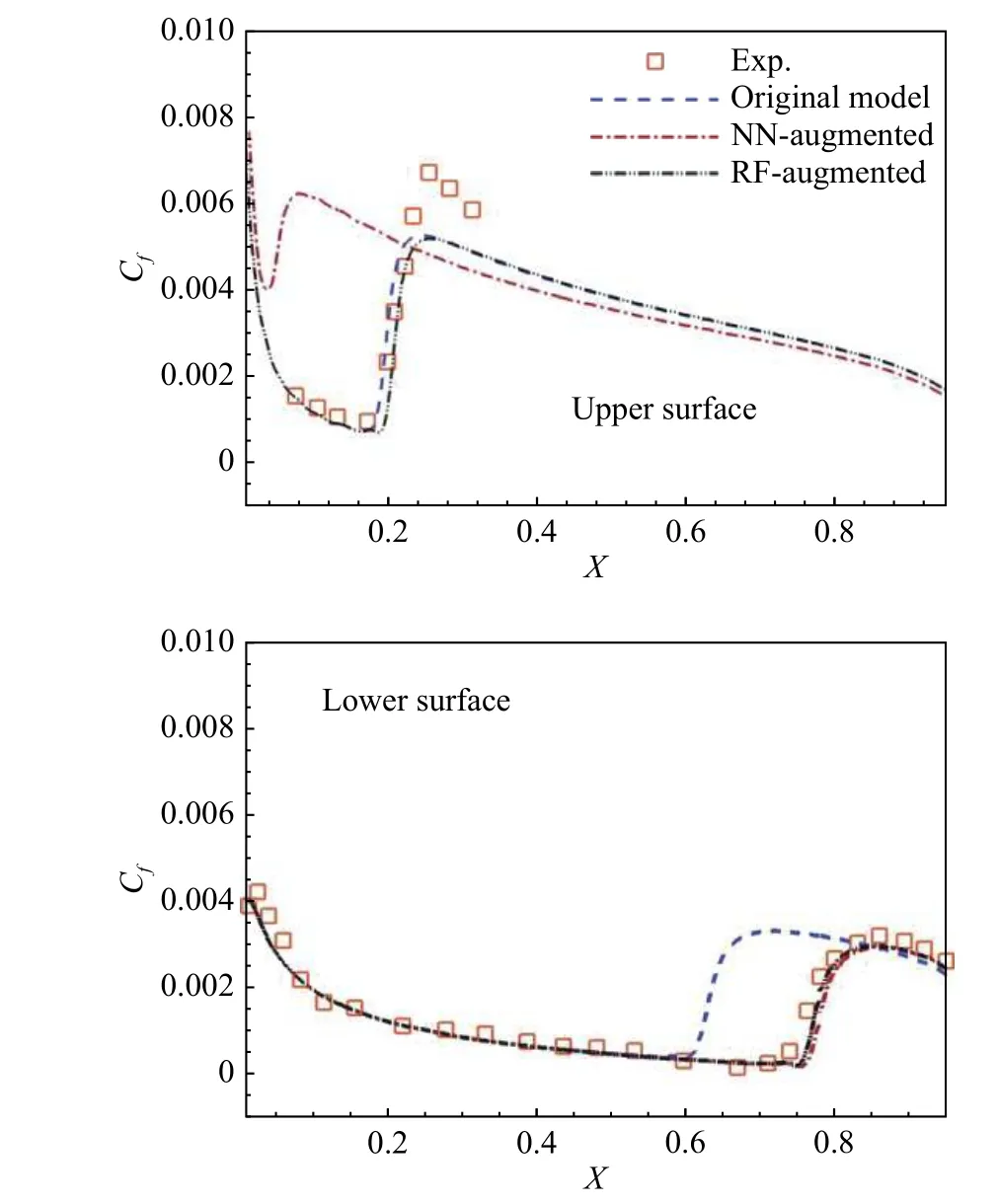
图10 NACA0012 转捩Cf 智能预测[54]Fig.10 Distributions of Cf for NACA0012[54]
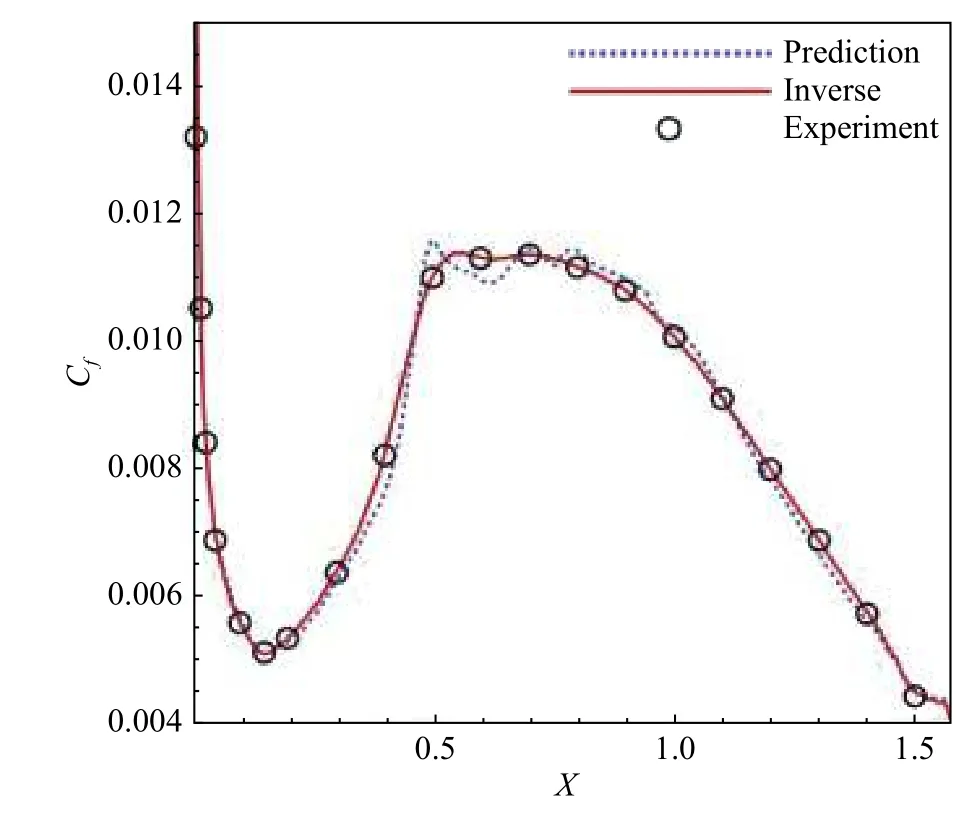
图11 T3C1 平板的反演及预测结果[55]Fig.11 Skin friction prediction for T3C1[55]
图21 为三种计算方式得到的压力系数及摩擦阻力系数分布对比。可以看出,引入神经网络模型修正后,激波位置后移,与DNS 计算结果基本吻合。表5对比了不同计算方法的分离泡信息发现,神经网络辅助的BSL 模型预测的分离泡大小将BSL 模型的计算结果从5 .49δ 减小为4 .84δ,精度提高了15%左右。图22和图23 分别表示神经网络修正后的不同站位点处和不同壁面距离处的速度型对比。从灰色虚线框中可以看出,近壁处分离区内的速度型在一定程度上得以改善。

表2 模型训练、测试算例[60]Table 2 Training and test cases[60]

图12 残差神经网络转捩建模框架[59]Fig.12 The residual neural network (ResNet) transition modeling framework[59]
1)基于卷积神经网络的流场预测。在计算机视觉等相关领域,卷积神经网络是组成深度学习模型的基础组件。在早期的流场预测问题研究中,一般将流场数据等同于图像数据进行处理,如Thuerey 等[27]采用U-Net 神经网络模型作为基础网络架构,以UIUC 翼型来流的速度场图像以及翼型几何的Mask图像作为网络的输入,以翼型的速度场以及压力场作为输出来构建相关的映射关系。结果表明在GPU 架构下,U-Net 网络(如图3 所示)仅花费5.53 ms 就可获得翼型周围的流场,而采用OpenFOAM 求解器去求解翼型的流场需要花费40.4 s。Guo 等[28]较早地将机器学习方法引入到空气动力学领域执行多几何的流场预测任务,提出了一种基于卷积神经网络的针对二维以及三维流场的非均匀定常层流流场的代理模型,进一步构建了符号距离场SDF 与待预测的速度场以及压力场的映射关系。测试结果表明该代理模型可以以较低的预测误差为代价,实现预测流场速度比基于GPU 加速的CFD 求解器快2 个数量级,比基于中央处理器(central processing unit,CPU)的CFD 求解器快4 个数量级。类似的工作还有Ribeiro 等[29]提出的DeepCFD,Duru 等[30-31]提出的CNNFOIL 等。结合空气动力学相关领域知识对卷积网络架构做了进一步的改进与研究[32-34],如:Wang 等[35]以及Omata等[36]使用深度卷积自编码器的数据驱动非线性降维表示方法对非定常流场进行了降维;Fukami 等[37]通过卷积神经网络(convolution neural network,CNN)和混合降采样跳跃连接多尺度模型从低维湍流数据中去重建高分辨率流场。上述研究大多数基于符号距离场,采用将流场数据映射到非均匀笛卡尔网格的处理方式[38]。这种数据处理手段仅能预测固定维度的流场数据且在面对包含深度几何特征的流场预测任务时,像素化势必会导致流场信息的缺失,难以表征近壁区的流场特征,甚至可能会产生非物理解[39]。为获取高精度的流场仿真结果,构建相应的深度学习模型过程中应考虑以下几个重要因素:(1)构建有效表征物理边界条件、流动信息与待预测流场之间的强映射关系;(2)高效的深度学习流场特征提取器;(3)有效的优化目标即损失函数;(4)精细化的深度学习模型训练策略。

图13 计算流程图[62]Fig.13 Flow diagram for estimating transition location[62]

图14 神经网络转捩建模计算方法[64]Fig.14 Proposed neural network for transition modeling[64]
本团队主要在第二、第三领域开展了智能转捩建模研究,即转捩模型性能的智能提升以及基于人工智能算法的智能替代模型。在团队前期开发的适用于高速边界层转捩模拟的C-γ-Reθ模型[65-66]基础之上,着眼于模型性能在特定工况、模态的提升以及转捩模型的智能高效替代两个方面。C-γ-Reθ模型基于稳定性理论、实验与 DNS 数据和转捩准则多层级融合的建模思想,建立充分考虑可压缩、横流、粗糙度等因素的高超转捩准则与预测模型,对于三维复杂外形高速转捩具有良好的模拟能力[67]。模型在升力体[61,68]、圆锥[69-70]、椭锥[65]等系列工况中得到了全面验证。
在转捩模型的高超声速修正以及模型性能的智能提升方面,主要以特定工况与模态下原模型预测能力的不足进行针对性地改善。本研究团队[71]针对C-γ-Reθ模型在尖锥高超声速飞行试验工况下的迎风面中心线区域Mack 模态预测能力不足的问题,建立了转捩预测与飞行试验实测数据偏差深度神经网络映射,完成了飞行试验工况转捩热流修正,并推广至全弹道及其他外形飞行试验,使转捩模型在多模态共同影响下的预测能力更加精准,如图15 所示。
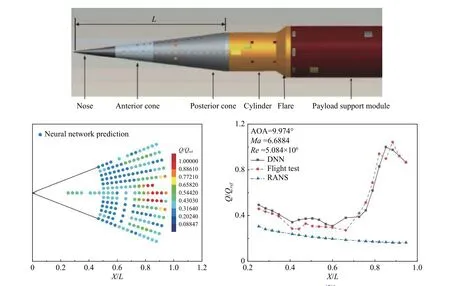
图15 人工智能算法对C-γ-Reθ 模型飞行试验工况的修正[71]Fig.15 AI modified C-γ-Reθ model under a flight test condition[71]
在智能替代模型研究领域,同样以C-γ-Reθ转捩模型为方法、数据基础,旨在采用机器学习方法建立更加高效的替代模型。本研究团队针对三维边界层转捩预测需求,建立了基于深度神经网络的“层流-转捩-湍流”三维预测模型,并与SST 湍流模型耦合,对CFD 求解平台中的转捩模块进行了智能替代,实现了亚跨声速条件下多种外形状态的三维边界层转捩高效预测,展示出智能转捩模型广阔的工程应用前景,如图16、图17 所示[50]。

图16 智能替代模型预测平板转捩及翼型转捩[50]Fig.16 Intelligent substitution model for predicting 3Dboundary layer transition of plate and airfoil[50]

图17 智能替代模型预测后掠翼和椭球标模三维边界层转捩[50]Fig.17 Intelligent substitution model for predicting 3D boundary layer transition of swept wings and ellipsoidal[50]
3.3 湍流建模
根据NASA 报告《CFD Vision 2030 Study》,RANS方法直到2030 年仍然将是湍流计算依赖的主要手段[72]。然而,被广泛应用的线性涡黏模型(S-A 模型、k-ω模型、SST 模型等)对于大分离、非稳态等复杂流动仍难以实现较好的预测精度。纵观过去近二十年的发展可以发现,尽管传统湍流模型取得一些进展,但对于大分离等经典难题仍难以实现质的突破和提升。湍流建模亟需从新视角借助新手段打破现有研究模式的局限性。随着人工智能技术的迅速崛起,在过去不足十年的发展过程中,基于机器学习方法的湍流建模研究工作和相关成果几乎成指数形式的爆发,成为当前流体力学、空气动力学研究的热点之一。综合而言,这些工作包含了二维、三维几何外形在不同速域条件下的附着和分离流动,主要可分为以下两个方面:1)对传统湍流模型的改善。研究者基于高可信度CFD 或实验数据通过机器学习方法提升传统模型对分离流等算例的预测精度,如图18 所示。其研究思路大致有两种:一种是通过改变模型的控制方程形式,如乘以修正系数或给方程增加源项。例如,Duraisamy 和Singh 等[73-75]将反演模型和机器学习结合起来重构更好的湍流及转捩模型的函数表达式;另一种是在RANS 模型基础上构造偏差函数,然后将RANS 模型和偏差函数的计算结果叠加作为最终的雷诺应力值。清华大学张宇飞团队基于不同建模方法也开展了相关研究[76-78]。例如,Xiao 等[79-83]提出了物理嵌入的机器学习(physics-informed machine learning,PIML)概念,强调了机器学习中包含物理知识的重要性。2)直接构建雷诺应力或亚格子应力的替代模型。例如,Ling 等[84]提出张量基神经网络学习非线性湍流模型。Novati 等[85]基于多智能体强化学习获得亚格子应力的封闭方法;西北工业大学张伟伟团队开展了高雷诺数湍流的涡黏封闭建模研究[86-89];南方科技大学王建春团队基于神经网络研究了亚格子应力及相关变量的建模方法及在可压缩湍流模拟中的应用[90-92];Weatheritt 等[93-94]和北京大学赵耀民团队[95]基于符号回归学习显式表达的非线性模型。更多数据驱动湍流建模的研究工作可参考综述文献[96-99]。

图18 基于机器学习的湍流建模研究Fig.18 Research on turbulence modeling based on machine learning
目前,现有的研究工作针对简单构型的中/低雷诺数湍流或低速流动已取得令人鼓舞的成果,但面向含激波/湍流边界层干扰等复杂流动现象的高速可压缩湍流的智能化建模研究还相对较少。Wang 等[80]基于冻结假设预测了高超声速平板湍流边界层中雷诺应力。本团队近期初步开展了针对雷诺应力偏差量的隐式表达形式-涡黏修正量的机器学习建模工作,尝试改善经典湍流模型对压缩拐角算例的预测结果,目的主要是探索建模策略的有效性和收敛性。本工作采用24°偏折角的压缩拐角标准算例作为研究对象,Ma=2.89,Re∞=5 581.4 mm-1,平板边界层厚度为6.7 mm。所采用的网格大小为2 160×160,其中物面第一层网格高度为1×10-5mm,对应的y+约为0.64,计算域如图19 所示。考虑到SST 模型预测的分离区明显偏大,本工作采用BSL 模型,其控制方程形式为:

图19 压缩拐角计算网格Fig.19 Grid for compression corner
模型的相关参数可参考文献[100]。
根据Wu 等的研究,如果显式表达形式的雷诺剪切应力存在误差,那么在N-S 方程迭代过程中时均场误差迅速增大[101],最终造成求解失败。目前主流的解决方法是构建湍流相关量的机器学习模型,然后基于冻结假设采用单向传值的方式直接将模型预测结果赋值到方程右端。然而,这种方法在工程应用中的局限性较大。由于DNS 计算的雷诺应力、时均速度场与RANS 求解器不自洽,因此无法直接基于DNS 数据构建机器学习模型,必须采用恰当的数据融合方法。本工作通过基于最小二乘法的线性涡黏反 算和加权平均实现DNS 雷诺应力与RANS时均场的融合。
传输方式:以D5000作为传输始端,D5000接收原始报文后,经规约转换,将遥信变位及全数据发至五防系统,五防系统将遥控许可信息通过上行通道发至D5000。
通过上述基于最小二乘的涡黏反算方法实现了DNS 数据与RANS 求解器的相容性处理,保证了数据的自洽性,因此获得了具有建模可行性的数据样本。基于这些样本采用神经网络构建RANS 湍流模型的修正模型。采用的机器学习模型架构为(16,16,16,16,1)的全连接神经网络。构建模型所采用的输入为流场时均变量的组合形式,如表3 所示,其中p、ρ、u、µ分 别表示压力、密度、速度矢量和动力黏性,k、ε、ω分 别表示湍动能、耗散率和比耗散率,S和R分别表示应变率张量和旋转率张量,‖·‖2表示二范数,abs 表示取绝对值,tr 表示求迹。模型的输出为反算优化后的涡黏与基础模型(baseline model,BSL)模型计算的涡黏之间的偏差Δμt。模型训练过程采用的损失函数为考虑正则化、L1 范数和近壁区雷诺应力约束的均方误差。
财政支农更精准 监督资金不手软——贵州省丹寨县财政推进“乡村振兴”战略侧记陈贵旭 刘世会 黄立祥6-66

表3 采用的输入特征Table 3 The adopted input features
模型训练前将数据随意打乱,选取其中的4/5 作为训练数据,剩余的1/5 作为验证集。训练过程在Pytorch[102]上实现,所采用的学习率及优化算法等参数如表4 所示。

表4 模型训练的参数设置Table 4 Parameters of model training
模型训练后将其集成至风雷求解器,实现机器学习模型与RANS 求解器的双向耦合迭代。图20 表示耦合机器学习模型的RANS 求解器的收敛过程演化图。从图中可以看出,经过大约44 000 步迭代后BSL 模型的阻力系数已基本收敛,残差在 4×10-6和5×10-6之间小幅震荡。引入神经网络模型开始修正后,阻力系数经过大约20 000 步迭代后实现再次收敛。值得一提的是,N-S 方程的残差基本保持不变,说明神经网络模型的嵌入并未破坏求解器的收敛性,从而验证了所提出建模策略具有双向耦合可行性。
常州科技人才原创性研发能力不强,技术成果缺乏,高水平重大科技创新平台和研发机构不多,高水平科技人才队伍和团队偏少,具有自主核心知识产权的原创性成果较少。常州缺乏产业特色鲜明、国内水平领先的园区。部分科技园区产业定位不明够确、服务功能建设不完善;常州高校对区域科技创新体系建设推动作用有待加强。
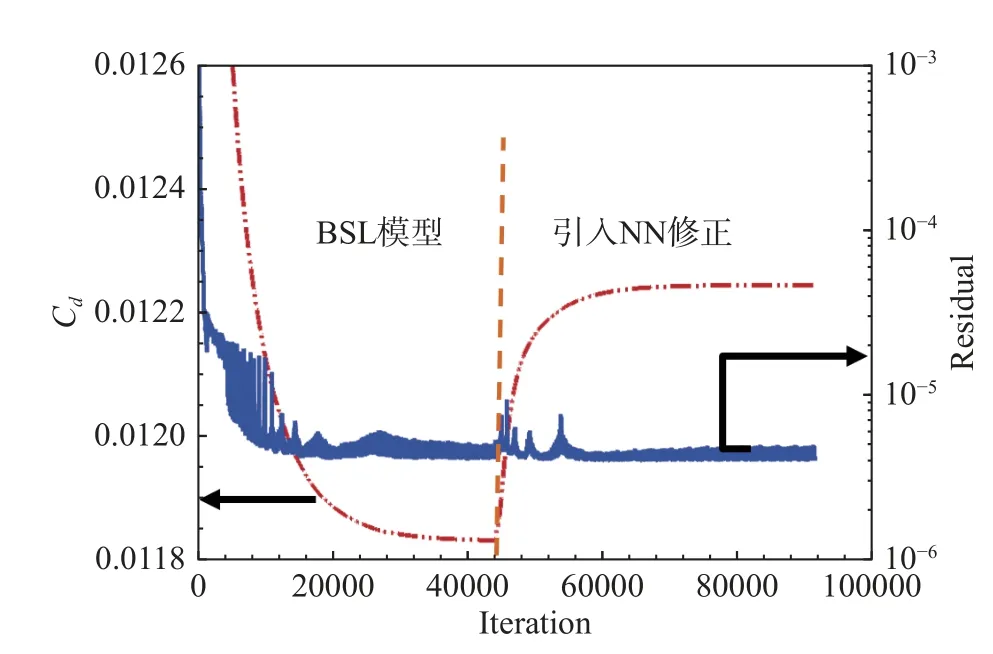
图20 耦合机器学习模型的RANS 求解器的收敛过程Fig.20 Convergence of RANS solver coupled with machinelearning model
第三个领域是采用人工智能相关方法,直接构建数据驱动的转捩替代模型。由于大多数替代模型是直接基于大量转捩相关数据驱动的,并且模型并不显含描述转捩过程的相关物理机理,因此该类人工智能转捩模型被称为黑箱模型。该类模型通常采用神经网络算法构建复杂代数模型,用以替代现有转捩模型,并耦合至现代CFD 中,实现传统转捩模型预测水平的高效转捩流场模拟。例如,郑天韵等[59]以SSTγ-Reθ模型的大量零压力梯度自然转捩平板的计算结果作为训练数据,利用深度残差网络重构了当地平均量与间歇因子γ之间的映射,发展了一种较为高效的人工智能转捩替代模型,如图12 所示。吴磊等[60]以SST-γ转捩模型的数值模拟结果为训练测试集,建立从平均流场信息到转捩间歇因子γ的人工神经网络映射,并与RANS 求解器耦合,实现了多种翼型下转捩位置的预测与转捩流场的模拟,取得了较好的泛化效果,如表2 所示。数据驱动的黑箱替代模型的泛化性能,很大程度上受训练数据的转捩主导模态、输入判据形式、来流工况等系列因素限制,难以做到普适。同时由于转捩物理过程的高度复杂性,基于物理约束的灰箱、白箱智能转捩建模,目前还在研究当中,未广泛见诸文献。
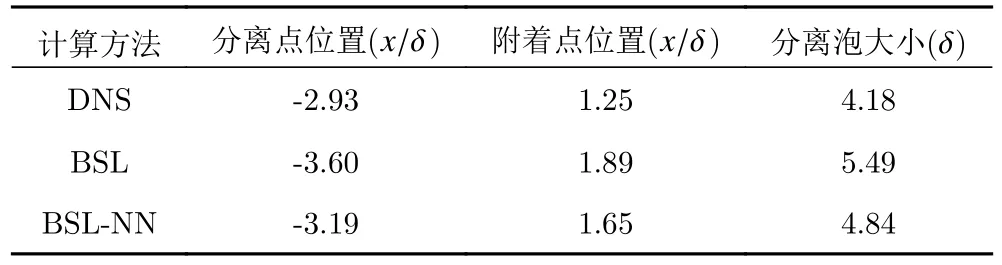
表5 不同计算方法的结果汇总Table 5 Results of different computation methods

图21 神经网络修正前后的压力系数及摩擦阻力系数对比Fig.21 Comparison of pressure coefficient and skin friction coefficient

图22 神经网络修正后的不同站位点处的速度型对比Fig.22 Comparison of velocity profiles at different monitoring points

图23 神经网络修正后的不同壁面距离处的速度沿流向分布对比Fig.23 Comparison of horizontal velocity along the x-axis at the same wall distance
3.4 多源数据融合
高精度的气动数据是飞行器总体设计的依据,是确保飞行器研制成功的基本前提和重要保障。获取气动数据的空气动力学研究三大手段(数值计算、风洞试验和飞行试验)各有优缺点,单一研究手段难以准确预测飞行器气动特性,在工程上需要融合多手段多来源的数据,以得到对气动特性较为准确和完善的描述[103]。但是,气动数据的融合与传统信息领域的数据融合存在一定差异,主要体现在传统信息领域的数据融合隐含了“多源数据都源于同一对象,对应的理论真值相同”这一条件。而在空气动力学研究中,不同研究手段所研究的物理对象通常是不同的,如风洞试验采用的是缩比模型,CFD 数值计算对象通常是刚体模型,飞行试验的对象则是真实飞行器,这三种情况下的气动力真值理论上是不相同的,因而此时的数据融合还需考虑不同来源数据之间的数据关联与同化问题,如图24 所示,可采用的方法主要包括:选取关联参数的方法(亦称为Scaling 方法)[104-105],对差量或比值建立模型进行融合的方法[106],Cokriging 方法[107]和基于深度神经网络的融合方法。基于深度神经网络的融合方法又主要包括基于迁移学习的融合方法[108]和基于多可信度神经网络(multifidelity neural network,MFNN)的融合方法[109],其中迁移学习方法是针对具有大量数据样本的数据来源(通常认为是易于获取的低可信度数据)进行神经网络模型训练,然后将训练好的模型迁移至目标任务,即针对另一来源的数据(通常采用获取成本较高的高可信度数据)进行模型系数的微调,从而将低可信度数据的规律蕴含在神经网络模型中且又融入高可信度数据的信息,从而实现了两种来源数据的融合。
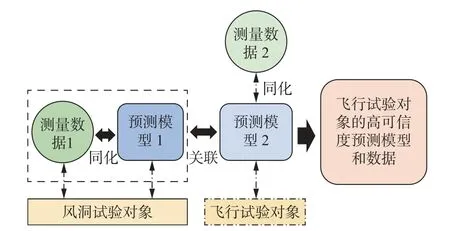
图24 气动数据关联融合示意图Fig.24 Illustration of aerodynamic data correlation and fusion
除了上述融合分类方法,按照融合对象数据抽象层次的不同,又可将数据融合分为数据级、特征级和决策级的数据融合,详细论述可参考文献[110-111]。在气动研究中,直接针对不同来源气动数据的融合属于数据级的融合,而对数据进行本征正交分解(proper orthogonal decomposition,POD)、动力学模态分解(dynamic mode decomposition,DMD)等特征提取后,在模态特征层次进行融合,则属于特征级融合[112-113]。文献[114]针对2.4 m 暂冲型跨声速风洞的高精度流场控制问题,提出了一种基于已有工况模型与新工况模型融合的方法,使马赫数精度达到0.001 的水平,这属于决策级的融合。基于随机森林、集成学习的气动建模方法在一定程度上也可以视为决策级的融合问题[115]。
数据融合的核心是融合准则,目前常用的融合准则包括基于数据方差的加权融合准则、贝叶斯融合准则、基于模型相关度的融合准则、基于D-S 证据理论的融合准则、基于高斯过程的融合准则、基于卡尔曼滤波的融合准则等。近年来,基于神经网络的数据融合方法发展较快,其核心是将数据融合视为一种复杂的非线性映射机制,通过神经网络的方法来对这种机制和内蕴融合原则进行学习和模拟,例如上面提到的MFNN 已在工程上已得到了应用验证[116]。近期Meng 等进一步提出了一种新的贝叶斯神经网络框架,可训练带噪声的多精度数据,并证明该方法可以自适应地捕捉多种保真度之间的线性和非线性关系,进一步减少数据的不确定性[117]。
我们结合如下典型算例对MFNN 进行了实现,并分析了高可信度数据噪声和低可信度数据噪声(σ=0.1)对融合结果的影响,如图25。
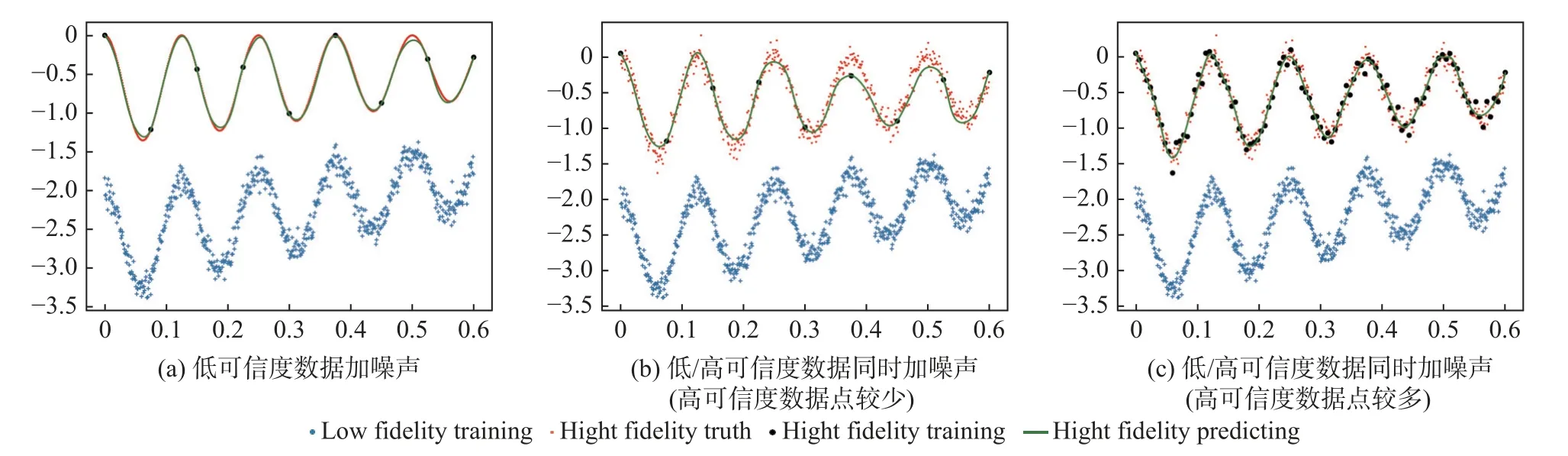
图25 MFNN 中数据噪声对融合结果的影响Fig.25 Effect of data noise on fusion result in MFNN
除上述方法外,数据融合方法可具体参见本文3.4 小节。表1 列出了智能空气动力学的研究方法与空气动力学传统研究方法的差异。就理论分析手段而言,传统研究方法依靠的是公式推导、数据统计分析与归纳演绎,而智能空气动力学则可借助大数据中的数据挖掘、专家系统的知识表示与推理等方法来辅助知识发现;就CFD 计算手段而言,传统方法主要基于有限差分或有限体积法对N-S 方程进行数值求解,智能空气动力学则可采用神经网络求解微分方程的方法;就风洞实验手段而言,传统研究方法主要遵循的是实验设计、风洞运行、数据采集与对比分析的串行流程,而智能空气动力学的风洞实验可开展基于数字孪生的平行试验和自主试验;就模型飞行试验手段而言,传统研究方法通过气动建模与参数辨识获取飞行状态下的气动系数,而智能空气动力学可将气动建模与强化学习进一步结合,实现学习飞行和“端到端”的智能控制。更多研究方法及其在航空航天工业中的应用可参见文献[22]。
拓展MFNN 使其适应非定常气动数据的多输入和多输出数据结构,然后利用该网络对某翼型的非定常CFD 和风洞试验气动数据进行融合。具体而言,将CFD 数据作为低保真度数据,而将风洞试验数据作为高保真度数据进行融合。选取缩减频率为0.02、0.04、0.08 的非定常气动数据集作为训练集,并将缩减频率0.06 的数据集作为测试集,结果如图26 和表6 所示。同时,我们利用LSTM 直接对风洞试验数据进行非定常气动建模,并将其结果与MFNN 融合结果进行了对比。可以看到,基于MFNN 的非定常气动数据融合精度显著优于LSTM 方法的预测精度。
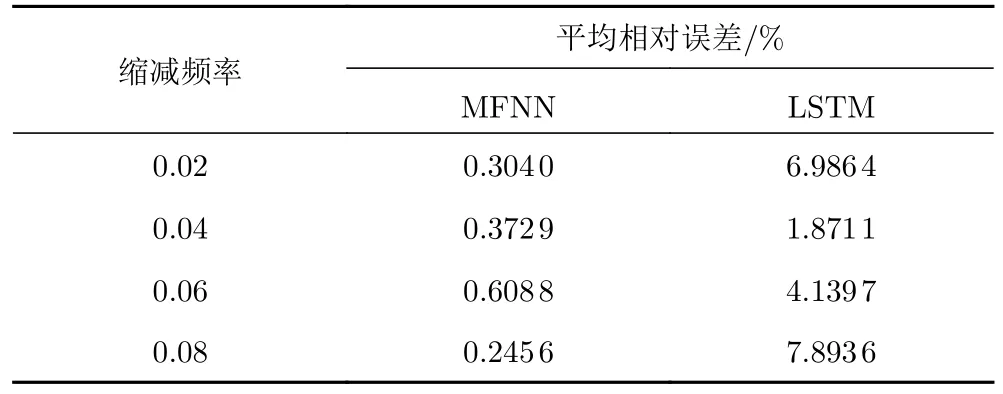
表6 基于MFNN 的非定常气动数据融合结果与LSTM 预测结果对比Table 6 Fusion result comparison of unsteady aerodynamic data based on MFNN and LSTM
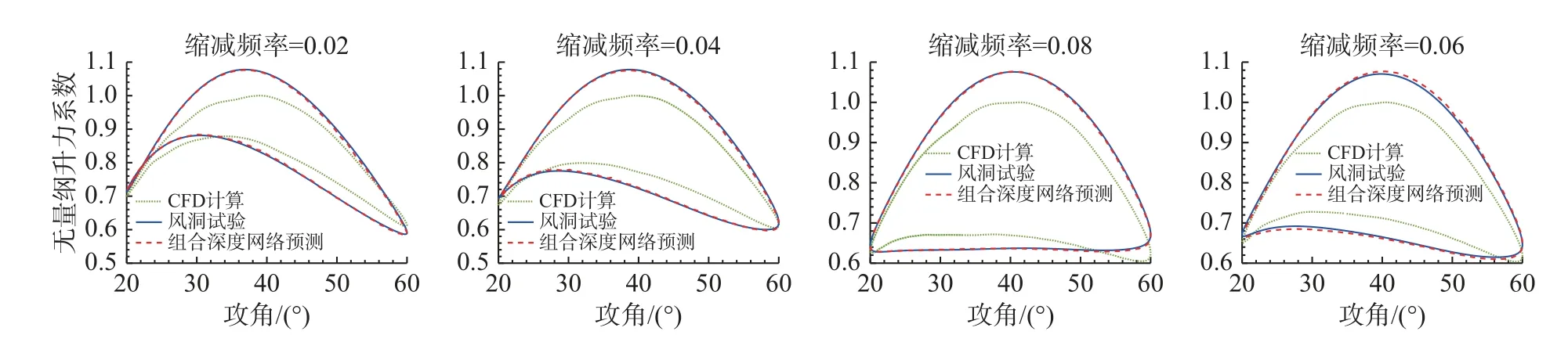
图26 基于MFNN 的非定常气动数据融合结果Fig.26 Fusion results of unsteady aerodynamic data based on MFNN
3.5 气动力/热建模
人工智能求解气动性能的方法主要分为两类:一类是数据驱动的有监督神经网络方法;另一类是物理驱动的无监督学习方法。数据驱动方面,Ladicky等[118]采用回归森林(regression forests,RF)方法成功对非定常流场气动性能进行预测,大大提高了数值计算效率。Guo 等[28]采用卷积神经网络(CNN)方法对二维和三维层流建模并进行流场预测,在保证较低错误率的前提下,其计算效率分别比基于GPU 加速和传统CPU 的CFD 解算器提升了2~4 个数量级。Wang 等[119]采用生成对抗网络对翼型压力系数进行了智能预测,计算效率提升3 个数量级,同时误差控制在3%以内。Sekar 等[120]提出一种快速预测翼型流场的深度神经网络方法,在二维定常层流流场预测中取得了较好的效果。Fukami 等[37]提出了基于机器学习的湍流场超分辨率重建方法。物理驱动方面,以Raissi 等[121-123]引入物理嵌入的神经网络(PINN)为代表,PINN 求解偏微分方程,通过特定流场的若干观测值对神经网络进行训练,以控制方程作为约束,并不需要引入边界条件就可实现对特定区域的流场预测,其通过在损失函数中引入偏微分方程作为约束条件,仅用少量数据就可以完成模型训练。Zhu[124]和Geneva[125]等采用卷积编码-解码神经网络模型对偏微分方程进行了数值求解,利用CNN 卷积核表示高维流场数据,大幅降低求解难度,同时在代价函数中融合边界条件与控制方程,从而减少了对于数据的依赖程度。更多关于数据驱动方法赋能气动力和气动热建模的工作可参见文献[126-127]。
目前已有多种气动智能建模方法在不同应用中取得了较好的效果。但是这些方法仍然存在一些问题:1)各类方法预测得到的不同气动参数精度差异较大;2)已有方法的研究基本聚焦于特定外形和特定场景,对于外形和应用场景的泛化能力不够;3)大多数工作仅采用均方误差作为代价函数,忽略物理约束。产生这些问题的原因主要包括以下几个方面:1)大多数方法采用相同的网络结构直接预测不同的气动参数,缺乏对不同气动参数差异性的刻画和表示;2)用于训练模型的气动数据库通常较小,通常仅在特定外形的不同飞行状态进行数值模拟获得训练样本;3)对于物理机理的凝练和抽象不够,导致方法无法满足某些显而易见的物理规律。
3.5.1 气动力智能建模
为解决这些问题,实现飞行器气动特性的快速精确预测,本团队近期开展了一种多任务气动性能智能建模方法,设计了基于多任务学习的神经网络(multitask learning neural network,MTLNN)模型,在MTLNN模型基础上,提出了内嵌物理知识的PIMTLNN 模型,并面向战术导弹开展了模型验证。由于PIMTLNN模型引入了气动特性参数之间的物理机理,模型对训练样本数量的依赖程度降低,可以进一步节约数据获取成本,为气动优化设计提供有力工具。
LocalGeoNet 用于捕获需要预测的指定点周围的局部形状变化。它的输入是一个 14 维向量,由一个坐标部分和一个局部形状部分组成。坐标部分反映拓扑结构,包括笛卡尔坐标、球坐标以及x-y平面上的投影点与坐标系原点之间的距离。局部形状部分反映指定点附近局部形状的变化,由法向量、最大主曲率、最小主曲率、高斯曲率和平均曲率组成。法向量和曲率由相邻点拟合的局部曲面得到。

图27 内嵌物理机理神经网络模型的结构框图[128]Fig.27 Framework of physics-embedded neural network[128]
图28 展示了本团队提出的两种模型性能,从轴向力系数、法向力系数、俯仰力矩和压心位置的预测结果与CFD 计算结果的对比来看,MTLNN 和PIMTLNN 模型的气动性能随迎角变化的趋势与CFD 计算结果相吻合,但细节图可以看出,PIMTLNN模型预测结果更接近真实值,表明其在相同数量样本下具有更强的学习能力。
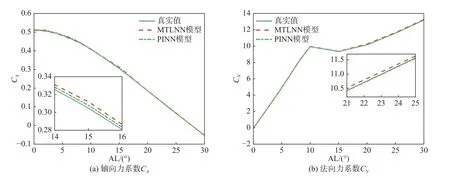
图28 内插情况下轴向力系数、法向力系数、俯仰力矩系数和压心位置的预测结果[128]Fig.28 Prediction of axial force coefficient,normal force coefficient,pitching momentum coefficient and pressure center location of interpolation cases[128]
基于数据驱动的模型预测精度受测试样本集取值范围的影响。测试集在训练集包络范围内,预测精度会较高;测试集在训练集包络外,预测精度会有所降低。为验证模型泛化能力,本团队对外插情况下的4 种气动系数进行了预测并与真值比较,如图29 所示。PIMTLNN 模型的预测精度较 MTLNN 模型的预测精度更高。物理机理信息的引入,使模型具有更强的外插泛化能力。
基于 PINN 模型的预测误差值相对较小,CA、CN、Cmz及Xp预测结果的均方根误差(root mean square error,RMSE) 分别为 0.003 360、0.031 943、0.056 021、0.003 208,MRE 分别为0.995 6%、0.241 5%、0.639 2%、0.590 4%,如图30 所示。可以看出,两类模型的轴向力系数CA的预测精度基本相近,MTLNN模型的平均相对误差(Mean Relative Error,MRE)指标比基于PINN 的模型略低,主要是因为PINN 模型中未考虑CA的物理机理,其他3 个气动特性参数的训练过程可能影响到模型共享层的部分网络参数,导致CA的预测精度受到一定的影响。
轩辕明从信封里拿出一张小纸条,展开一看,不禁眉头紧锁。黑火儿、奇巧生、翼小飞都凑了过来。“老师,校长又给您写了些什么?”黑火儿问道。

图30 外插情况下 CA、CN、Cmz、Xp 的预测值与真实值的RMSE 和 MRE[128]Fig.30 RMSE and MRE of predicted and label values of CA,CN,Cmz,and Xp of extrapolation cases[128]
3.5.2 气动热智能建模
受企业传统管理结构模式所影响,信息的传递时间较长,而且传递的速度较慢,这就在无形中降低了工作的效率,同时违背了信息化的特点,这种模式不利于企业的长远发展,对企业的发展有一定的阻碍。所以,企业应该根据信息化发展的特点,改变组织结构,提高信息的传递速度,实现企业中各部门的信息互通有无,保证信息的准确性和安全性,提高企业的信息化管理水平,所以扁平化组织结构的出现,正好实现了该内容,它不仅能够保证信息之间的连贯性和有效性,同时也提高了管理水平。
为提升高超声速飞行器气动热预测效率,设计了自适应外形的气动热智能预测模型SA_HFNet。该模型采用点对点的方法预测飞行器壁面热流。给定飞行器形状、飞行条件和飞行器表面指定点的坐标,可以高效地预测相应的热流值。预测模型由4 部分组成:用于捕捉全局形状变化的神经网络GlobalGeoNet,用于捕捉指定点周围局部形状变化的网络LocalGeoNet,用于获取飞行条件特征编码的网络FlightCondNet 和用于预测壁面热流的解码器HeatDecoder[129]。SA_HFNet 框架如图31 所示。
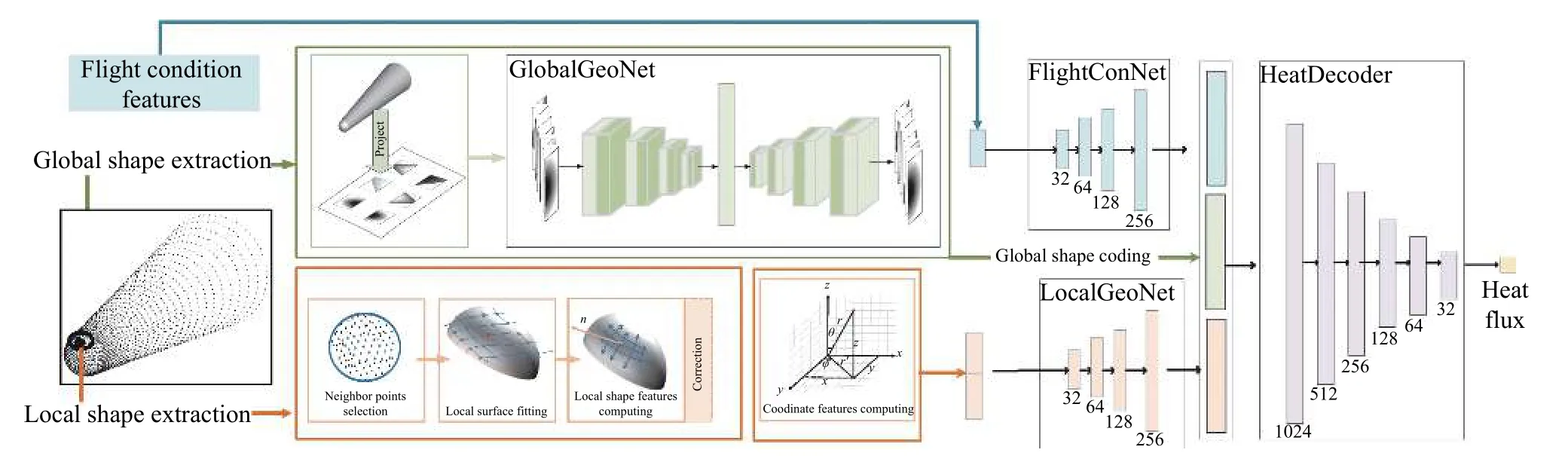
图31 自适应外形的气动热智能预测模型框架[129]Fig.31 Model framework of intelligent aerothermal prediction for adaptive configuration[129]
为了捕捉全局形状的变化,本团队将三维飞行器从上下左右前后6 个方向投影到二维图像上,并使用GlobalGeoNet 提取这些投影图像的特征。GlobalGeoNet由编码器和解码器组成。编码器提取投影图像的特征,并获得固定长度的全局形状编码。解码器根据全局形状编码重建投影图像。通过计算重建图像和投影图像之间的残差来调整 GlobalGeoNet 的参数,见图32。

图32 全局形状特征提取网络[129]Fig.32 Network of feature selection for global shape[129]
模型分为两个模块:用于提取共享参数的共享层和预测各个任务的特定任务层。由于气动特性参数之间满足一定的物理约束,即法向力系数CN、俯仰力矩系数Cmz和压心位置Xp满足函数f(CN,Cmz,Xp)=0。将这一公式嵌入神经网络模型中,作为模型训练过程中损失函数中的Jp(w,b)部分,具体的PIMTLNN 模型的结构如图27 所示[128]。所涉及的战术导弹采用了X-X 型结构,正常式气动布局,CN、Cmz和Xp的物理关系为:CN·Xp+Cmz=0。物理约束的引入,能够减少特定任务层训练的难度,减少训练对数据量的依赖程度,增强模型的泛化能力。
特殊情况下,拟合曲面不能代表正确的特征,如图33 所示。可以观察到,错误拟合的曲面直观地对应于曲率的奇异值。在 SA-HFNet 中,校正阶段旨在获得正确的局部形状特征。在校正阶段,沿着流线遍历所有点,以定位曲率突然变化的位置,通过在异常位置附近添加点,可以更精确地表示局部曲面。
乡村旅游是展示江城县美丽乡村建设成果的最好舞台,采摘旅游是人民群众青睐的休闲方式,不仅让客人体验了农家生活的乐趣,还拉近了游客和果农的距离,创造了一个新的销售模式,实现了游客满意消费,种植户收入增加的双赢。
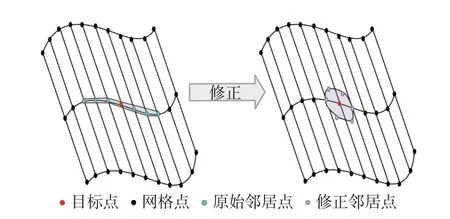
图33 拟合曲面在纠正前(左)和修正后(右)Fig.33 Fitting surface before (left) and after (right) modification
为探索SA_HFNet 的可靠性,评估了4 类典型高超声速外形中平均相对误差最大(MREall)的测试样本的表现效果,并在图34 中可视化样本的壁面热流。由图可以看出,即使这些最坏情况的样本,预测热流的极值和变化趋势与真实值也几乎是一致的。左列显示了 CFD 模拟的热流结果,中间一列显示了SA-HFNet 获得的热流,右列显示了左侧和中间两列中用黄色线标记的流线上的热流。
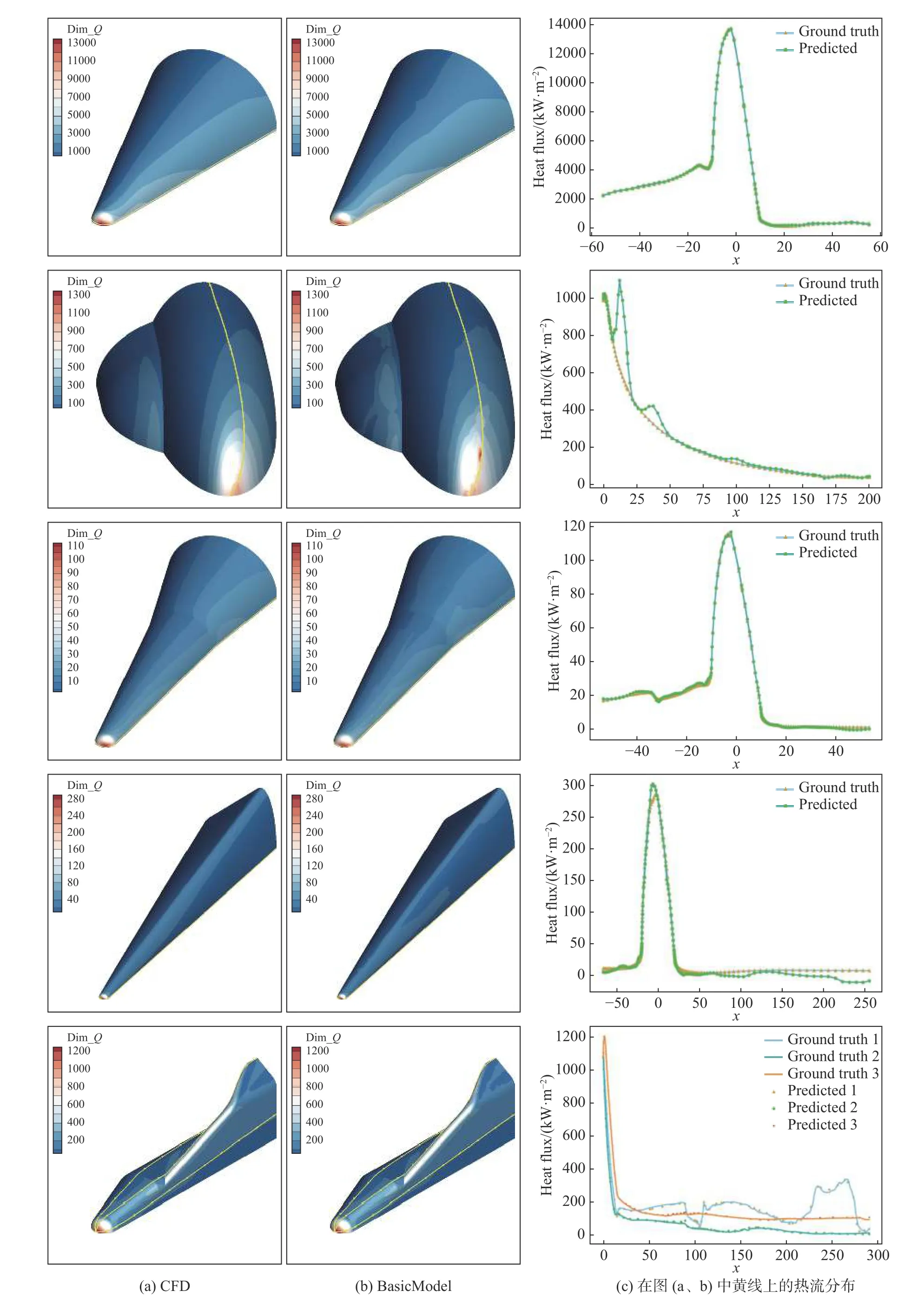
图34 最大M REall 样本预测结果可视化[129]Fig.34 Visualization of prediction results for maximum MREall samples[129]
为了测试 SA-HFNet 结构是否适用于训练集以外的形状,我们使用 4 种基本形状(钝锥、双椭球、双钝锥、升力体)训练了 BasicModel 模型,并在不同飞行条件下对航天飞机外形进行测试。200 个测试样本的MREall如图35 所示。可以看出,约 75% 的测试样本的 MREmax值低于3%,约 98% 的测试样本的 MREw值低于50%,表明使用 BasicModel 模型对航天器的预测结果具有参考价值。本文还对壁面机翼流线上的热流的 CFD 结果与 BasicModel 模型的预测结果进行了比较,如图36 所示。可以看出,BasicModel 模型能够准确预测航天器头部的热流,但难以捕捉机翼上的高热流。

图35 测试用例 MREall、MREw、MREmax 分布(横轴表示样本编号)[126]Fig.35 MREall,MREw,and MREmax distributions of test cases(Horizontal axis represents sample number)[126]

图36 航天器最大M REall 样本预测结果可视化[129]Fig.36 Visualization of prediction results for maximum MREall samples of space craft[129]
3.6 流场特征信息提取
3.6.1 涡特征智能提取技术
涡特征被认为是流场中比较重要的空间结构,是流体运动的肌腱,在工程中发挥重要的作用,因此涡特征的准确提取对于研究流场的规律和机理具有重要意义。随着计算能力的提升,数值模拟产生的流场越来越大,流场结构越来越复杂,研究人员从海量流场数据中提取空间特征难度不断增大。
目前,常用的旋涡提取方法大致分为三类:局部方法、全局方法和基于机器学习的方法。局部旋涡特征提取算法是逐网格点或单元进行识别,且计算时仅需要在各流场网格点或单元的局部邻域内进行操作,通常与流体在局部的旋转特性相关;而全局方法则需要对多网格点或单元进行检查以识别是否属于旋涡结构,一般是依据一些流场粒子运动轨迹的连贯性。旋涡结构本质上是具有全局性的,利用全局方法来识别旋涡结构是很合适的,但是它的计算代价要比局部方法高,故流场中常用旋涡特征提取方法都是基于速度梯度张量的局部方法,必要时为了核实旋涡结构识别结果的精确性,才会采用全局方法。基于机器学习的方法分为有监督学习方法和无监督聚类方法,有监督学习方法通过训练模型利用局部和全局方法的优点,以实现准确率和计算成本的折中,对传统方法误检、漏检、计算复杂度较高等缺陷均有一定的改进。而无监督聚类方法是利用从几何信息(位置、轴向长度、径向长度、形状、体积等)、动力学参数(涡量、速度等)和物理属性(压力、压力梯度)等角度构建的旋涡特征向量,聚类分析该特征向量从而自动检测出流场中旋涡结构。
数据挖掘技术是基于统计理论、机器学习、人工智能等算法从大量的数据集中获取有用隐含信息,并通过规则和可视化等方式予以展现,形成知识发现的过程。近年来,数据挖掘技术在空气动力学研究领域已得到了初步应用,如流场结构特征提取[8]、机翼翼型设计知识挖掘[9]、飞行器气动布局设计知识挖掘[10]、基于飞行试验数据的气动建模和气动参数辨识结果可信度确认等应用[11]。和通常的数据挖掘相比,气动数据规律挖掘具有两个特点:一是数据种类较为单一,且样本相对较少;二是挖掘希望得到的是因果关系,而不仅是关联关系。对于数据种类和样本数较少的问题,主要采用仿真方法扩充、迁移学习等方法来克服;而对于因果关系的挖掘,符号回归是目前主要采用的方法,即“在符号空间中寻找合适的公式,以使得它能够描述指定的数据集”[12-13]。解决符号回归问题的主要算法有基于蒙特卡洛树搜索的强化学习算法[14]、遗传程序设计(genetic programming,GP)[15]和基因表达式编程(gene expression programming,GEP)[16]。目前,GP 和GEP 等进化计算方法已广泛应用于工程应用和科学研究各领域,如气动减阻主动控制的控制律设计[17]、基于张量不变量函数组合的湍流雷诺应力模型构建[18-19]等工作,均取得了比较好的应用效果。但是,算法也存在函数发现过程中由于单节点算力不足造成的进化速度较慢、传统算子选择和操作固有的随机性带来的进化效率不高、收敛速度较慢;分布式计算超参数较多、对问题、数据噪声和种群规模较为敏感,算子选择、超参设置的严重经验依赖导致进化结果得到解析表达式可解释性低等挑战性问题。针对随机突变和重组等简单算子进化效率较低的问题,研究者们提出了基于分布的数学方法或增强基因表达能力的表达方式;针对搜索效率的优化,提出了基于分布概率的算子、增强基因表达能力的个体表达、自适应调整小生境半径的多样性策略、定期增加预测错误的样本权重和更新加权适应度、使用基因符-染色体序列频数表实现基因空间均匀分布初始化等改进策略。此外,通过将算法移植到Spark 框架的分布式架构,采用图形处理器(graphics processing unit,GPU)来进行并行加速,也可显著提高计算效率。
为提升空间特征提取效率与精度,本团队设计了一系列涡特征智能提取算法,团队主要贡献包括:第一,提出一种基于U-Net 结构的涡特征提取网络,如图37 所示,由收缩路径和扩张路径组成,收缩路径用于获取上下文信息,扩张路径用于精确定位,并将上下文信息向更高分辨率传播,使得输入与输出分辨率一致[147];第二,采用分块策略,将局部块作为网络输入,通过这种思路,一个标记流场就可以生成许多的训练样本,更多的训练数据将带来更好的网络性能,故分块策略可以有效避免性能下降;第三,为考虑流场网格点间的拓扑信息,采用涡量场局部块作为Vortex-U-Net 网络的输入,涡量场是通过速度场和物理网格拓扑信息相结合的方法计算出来的,它保留了流场的网格信息;第四,为区分不同网格点的重要程度,设计了一种融合物理先验知识的加权交叉熵损失函数,以指导网络的学习过程,使得模型的预测结果合乎物理规律。在此基础上,团队进一步针对多物理量提出了多视图涡特征提取网络,进一步整合速度场、压力场、涡量场等多种流场属性,增加流场特征智能预测的准确性。

图37 基于U 型网络结构的流场涡特征提取方法示意图Fig.37 Schematic diagram of vortex feature extraction method field based on U-net structure
图38 展示了Vortex-U-Net 在二维翼型算例的涡特征提取可视化效果,图中比较了三种方法,可以看出,Vortex-U-Net 方法与真实情况最为接近,涡的数量、完整程度、位置、大小均与真值相似。不同行表示不同迎角的结果,随迎角的增加,Vortex-U-Net 能够持续表现出较好的性能,说明其稳定性较高。通过量化分析,Vortex-U-Net 网络的漏检率和误检率都更低。
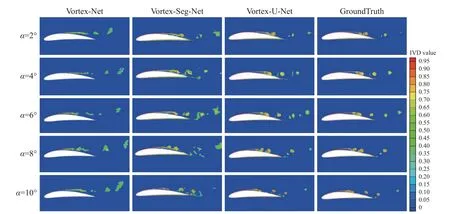
图38 不同预测方法在二维翼型绕流流场的预测结果比较Fig.38 Comparison of the prediction results of 2D airfoil flow field with different methods
图39 展示了Vortex-U-Net 在三维算例的涡特征提取可视化效果,图中比较了三种方法,三种方法对于翼尖涡和边条涡都能准确提取,但前两种方法的误检区域明显更大,图中红色虚线框表示误检区域。
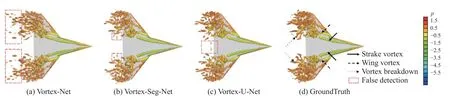
图39 不同预测方法在三维流场的预测结果比较[147]Fig.39 Comparison of the prediction results of 3D flow field with different methods[147]
3.6.2 非定常流场关键帧智能选取
未实行相关护理干预前两组血糖、血压情况对比差异无统计学意义(P>0.05),实行相关护理干预后观察组空腹血糖、餐后2 h血糖、收缩压、舒张压明显优于对照组,两组对比差异有统计学意义(P<0.05),见表1。
关键时间步选取方法是非定常模拟数据在时间维度上的一种数据缩减技术,选取的关键时间步能够完整反映流场的流动模式及演化规律。目前,对非定常流场关键时间步选取方法大致分为局部最优和全局最优两类方法。局部最优方法主要是基于贪婪法则将相似的时间步聚类分组,然后从每组中选取一个时间步作为关键时间步,计算开销较低。但是,这些方法只考虑局部时间范围内的流场数据,选取的关键时间步容易陷入局部最优,无法准确反映流场演化过程。全局最优方法是从整体最优角度考虑,主要采用基于聚类或动态规划等方法,实现关键时间步序列与原始整个时间步序列间流场信息差最小化,但计算成本较高。
互联网教育的第三个特点是就是在于学习对象的转变,在互联上你不仅仅是一个学生,你还可以摇身一变成为别人的老师,为他们答疑解惑。俗话说得好“三人行必有我师焉”一个人不可能永远是一个学生,有的平台可以把自己拍的视频发到网上供大家欣赏,还可以将自己的学习方法技巧,总结的知识点发到网上让别人来学习。这种交流式学习平台已经有很多网站开始建设了。
从局部最优角度考虑,Akiba 等[148]基于数据分布对相似的时间步结果进行分组,并从每组中选取出变化较大的时间步作为关键时间步流场。Wang 等[149]通过计算重要性曲线,以选择那些与其前一个最不相似的时间步作为关键时间步流场。Woodring 等[150]提出时间活动曲线技术来发现和突出显示非定常流场数据中的关键时间步。最近,Myers 等[151]设计了一种原位选取关键时间步的方法,基于分段线性模型假设来原位选取分段模型中的断点,并将该位置的时间步保存为关键时间步。Ling 等[152]基于特征重要性度量原位自动选取出非定常流场中关键时间步。Porter 等[153]使用深度学习框架进行关键时间步的选择,其具体过程如图40 所示,采用自编码器(autoencoder,AE)架构将流场编码为1024 维特征向量;然后使用tSNE 算法将2024 维特征向量降成2 维,形成整个非定常流场序列的二维图布局,最后,在二维图布局上使用基于弧长、基于角度或者两者混合的局部最优算法进行关键时间步选取。面向二维非定常流场,Liu 等[154]基于Siamese 网络[155]以有监督学习的方式从非定常流场数据集中准确获取时间步间的相似性度量,在此基础上,使用该度量对不同时间步进行比较分析,从而选取出关键时间步。
《自然》近日发表的一项研究称,全球变暖可能会导致“海洋热浪”(即海洋表面长时间的反常高温)的发生频次更高、袭击范围更广、强度更大。研究人员指出,1982年至2016年期间,海洋热浪天数增加了1倍。

图40 文献[153]的关键时间步选取流程图Fig.40 Key time step selection flowchart in Ref.[153]
从全局最优角度考虑,Tong 等[156]将关键时间步选取问题转化成整个时间步序列和关键时间步序列间相似性度量问题,采用基于动态规划的动态时间扭曲方法,使整个时间步序列和关键时间步序列之间的全局信息损失达到最小。Frey 等[157]提出了一种基于流的度量来计算时间步流场之间的距离,应用最小流方法捕获非定常流场数据中关键时间步。Da Silva等[158]将视频摘要方法应用于CFD 流场中关键时间步的选取问题。Lu 等[159]基于块匹配技术(Block Match)构建非定常流场的双向相似性度量矩阵(Bidirectional Similarity Metric),然后采用Kmedoids聚类方法来获取关键时间步。Liu 等[160]提出了一个基于事件的分析系统,用户可以交互式地在该系统的时间轴视图上为每个非定常流场选取关键时间步。
关键时间步选取是非定常流场可视化的研究热点,现有方法大多依赖于手工选定的数据特征,没有有效考虑流场潜在物理特性,选取结果无法准确表达流场中的流动模式。为解决上述问题,提出了一种基于深度学习框架的关键时间步选取方法KTSS+Net,如图41 所示。其具体流程为:1)采用融合流场物理特性的深度卷积自编码器(deep convolutional autoencoder,DCAE),以无监督学习方式来获取每个时间步流场数据的有效编码;2)借助流形学习的思想对整个流场序列的编码进行降维,并在低维映射空间上实现流场数据可视化;3)在该可视化图布局上使用DBSCAN 和Kmeans 混合聚类算法自动选取关键时间步。

图41 基于深度学习框架的关键时间步选取框架Fig.41 Framework of key time step selection based on deep learning
为验证关键时间步选取框架的性能,团队选择了4 种已有方法,并通过定常算例进行验证,如图42所示。观察发现,TimeCurve 选择的时间步更偏向于中间,前后均没有记录;ManifoldCurve 方法则更偏向于后面的时间步,对于前面的时间步记录较少;AE+K-medoid 方法记录较为均匀,无法反映其变化情况;MI+DP 与本团队方法KTSS+Net 对关键时间步的提取能更准确反映流场的变化情况。

图42 二维平板数据集中不同方法选取的关键时间步Fig.42 Selected key time step of 2D flat plane dataset with different methods
为了验证重构中间时间步流场数据的可用性,使用局部和全局两类可视化方法对线性插值重构和非线性重构的流场序列进行定性对比分析。从图43 观察到,基于关键时间步线性插值获取中间时间步流场数据丢失了大量的流场信息,容易对流场数据的后续可视化处理产生误差。基于自编码器非线性重构中间时间步流场数据能有效地代表流场的主要内容,保持流场信息的完整性,对后续的流场可视分析影响较小。这意味着KTSS+Net 方法既可以准确高效地选取出非定常流场中关键时间步,又可以有效地重构出中间时间步流场。更重要的是,该方法能在保证数据可探索性的基础上,只需保存关键时间步流场、训练好的自编码器和中间时间步流场数据的特征表示,大大减少了非定常流场数据的存储量,这对大规模多变量非定常流场数据可视分析与利用具有重要的意义和实用价值。

图43 线性插值和非线性重构的结果比较Fig.43 Comparison of the results of linear interpolation and nonlinear reconstruction
4 智能空气动力学研究展望
目前,智能空气动力学在流场快速预测、转捩预测、湍流建模、多源数据融合等领域得到了日益广泛的应用,取得了令人瞩目的研究成果,预示了该研究方向的积极前景。但与此同时,现有研究也面临着一定的挑战:一是领域数据的小样本问题。由于获取成本较高,空气动力学数据通常是小样本数据,这给神经网络建模和学习都带来了困难;二是模型存在通用性、可解释性、可靠性以及泛化性不足等局限性,难以实质性地解决转捩、湍流等经典难题,并且在应用到工程实践过程中存在较大困难。对于普通用户而言机器学习模型尤其是深度神经网络模型如同黑盒一般,不能确切地知道其运行机理及决策结果是否可靠,这给模型的有效使用和泛化带来了威胁;此外,研究者大多依赖现有开源算法库(如TensorFlow、PyTorch、Keras 等)构建和训练基于相对少量算例的小规模模型,缺乏面向大模型的训练算法和经验。为此,我们认为智能空气动力学的后续研究工作可从以下方面开展:
1)领域大模型的构建和应用。
ChatGPT 的出现标志着智能化步入大模型时代。虽然它主要是针对自然语言处理构建的,但其“基础大模型+行业数据二次训练+场景微调”的架构同样适用于科学研究领域。目前,华为公司联合中国商飞和西北工业大学开发的AI 大模型参数量达到1 亿以上,能在超临界翼型的几何形状、来流参数发生变化时,实现大型客机翼型流场的高效高精度预测;除流场预测外,领域大模型的应用场景还包括根据输入条件快速预测气动特性的预示型大模型、根据设计目标和约束自动生成飞行器几何外形的设计大模型,以及将这些大模型耦合智能控制、任务规划等环节,替代基于专家系统的传统设计方法,快速高效地获取工况的力/热/流场等信息,缩短研制周期、减少研发代价,实现真正意义上的“智慧飞行”。
《法制晚报》在刊发这条消息时,配了一幅漫画。画面中的两个人,正举着手机飞跑。其中一个一边跑一边说:“快点,还有5公里,走访还没有完成!”这真是可笑,在大街上跑步,就算是走访吗?而某些上边的考核者,看的只是行走的里程数字。至于你在哪里走,去干什么,全凭“指下生花”。
左达把钢筋扔掉,道:“干什么?我还要问你呢,我以为你是要债的,差点把你杀了。嗯,怎么是你?我约的可是张仲平,他人呢?”
2)大数据、大样本的数据库建立。
目前空气动力学领域的数据数量和质量有限。人工智能尤其是深度学习技术首先在计算机视觉领域取得了巨大成功,这主要是因为大数据时代的到来,使得图片和视频数量呈几何级数增长,各种超大规模图像和视频数据集层出不穷。反观空气动力学领域,目前仍没有公开的且大家都能认可的数据集用于科学研究。究其原因主要有两个:一是数据产生困难,空气动力学领域产生的数据有多种模态,不同模态的数据存在工况不足、覆盖面不够、数据污染、确定性与完整性差等问题;二是难以标注,深度学习系统需要大量有标签数据,而流场等数据对于某些问题的研究尚不存在客观方法,只能通过主观判断打标签,因此产生的标注数据存在一定的主观性,从而导致公信力不足等问题。文献[161]中给出了4 种解决方案,即基于模型微调、基于数据增强、基于度量学习和基于元学习的方法。针对气动领域数据的特点,可重点考虑基于数据增强和基于元学习的方法。基于数据增强的方法旨在获得与小样本数据相同分布规律的扩充数据,而基于元学习的思想则是使用少量样本数据,习得适应多种学习任务的共性特征表达,从而使得元学习模型在经过不同任务的训练后,能很好地适应和泛化到一个新任务[162-163],也就是学会了“如何学习的学习方法论”(Learning to Learn)。这一问题也是文献[164]中列出的人工智能10 个重大数理基础问题之一。除上述4 种方法,还可以借助主动学习方法,主动选择最有价值的样本向专家查询标记,从而显著降低模型提升性能所需要的样本数。此外,从领域大模型的角度出发,后续工作可加强构建智能空气动力学研究所需的大规模、超大规模数据库,利用大量数值模拟数据作为基础数据,并使用高精度的风洞试验和飞行试验数据进行补充。采用尽量客观准确的方法获得相关研究的标签,形成准确性高、客观性强、覆盖面广的智能空气动力学数据库。
3)自主研究算法的开发以及与硬件的深度融合。
尽管目前已有Keras、TensorFlow、PyTorch 等开源算法平台,但是针对大模型训练的开源技术和方法相对稀少。国内更是缺乏面向大模型的具备自主知识产权的智能化算法,亟需数学、计算机等领域研究人员创新性地提出新算法,实现软、硬件平台的开发,形成新的空气动力学计算架构,为大模型的开发和构建提供技术支撑和坚实保障。例如DeepMind 发布的AlphaTensor 为矩阵乘法等基本计算任务设计更高效的经典算法,有望大幅提高CFD 计算效率[165];而更进一步,采用神经网络求解流动微分方程,结合GPU、TPU、NPU 等专用芯片[166],可构建无需生成网格,无需差分格式离散的全新CFD 求解架构,在求解效率和使用便利性等方面全面超越传统CFD 计算方法。
致谢:在本文撰写过程中,中国空气动力研究与发展中心的蔺佳哲、孙国鹏、杨志供、邓亮、王天、西北工业大学的左奎军,分别整理了气动力智能建模、气动热建模、非定常流场关键帧提取、流场预测的相关文献,在此表示感谢!

