基于响应面法的高铁隔震桥梁地震风险分析

张添俊,赵桂峰,马玉宏,石 岩,陈发扬

(广州大学 a.工程抗震研究中心; b.广东省地震工程与应用技术重点实验室/工程抗震减震与结构安全教育部重点实验室; c. 土木工程学院,广东 广州 510006)

随着我国高铁建设事业的发展,部分线路不可避免地建在高烈度地震区域内,高铁桥梁的抗震性能成为需要着重考虑的关键问题。摩擦摆支座具有刚度大、位移大以及自复位等优点,在遭受地震作用时可以延长结构的自振周期,通过轨道面摩擦消散地震能量,其作为高铁桥梁的隔震支座极具优势。张常勇等[1]通过数值模拟对连续梁桥采用摩擦摆支座隔震前后的结构地震能量响应进行了对比,结果表明,摩擦摆支座的高耗能能力可大大降低结构的耗能要求。邵长江等[2]进行1/10缩尺的摩擦摆支座连续梁桥的振动台试验,结果表明,摩擦摆支座的隔震效果随着地震波地面峰值加速度(Peak Ground Acceleration,PGA)的增高而增强。邓细鹏等[3]建立摩擦摆隔震高铁桥梁非线性分析模型,对模型进行罕遇地震和极罕遇地震作用下的地震响应分析,结果表明,摩擦摆支座在罕遇地震和极罕遇地震作用下均能有效降低结构的地震响应。由于摩擦摆支座在高铁桥梁的应用相对较晚,缺乏其遭受极端地震作用下的抗震性能相关资料,而高铁对于我国经济发展起着举足轻重的作用,其在地震中的破坏可能导致交通中断,进而造成不可估量的经济损失。因此,评估高铁桥梁在将来可能地震下的风险程度,衡量其在地震下的经济损失和全寿命费用是十分必要的。

5.坚持以上率下。榜样的力量是无穷的，领导机关和领导干部位高权重、责任重大，因而对下级党组织和党员干部具有示范和引领作用。领导机关和领导干部带头践行党内政治生活和修身律己，就能为下级党组织和党员、干部树立榜样和参照，从而在全党形成一级做给一级看的良好态势。习近平同志强调：“要以上率下，从中央政治局常委会、中央政治局、中央委员会做起。”[2]

地震易损性分析是评估结构失效损失和全寿命费用的基础,主要包括增量动力法[4]、云图法及响应面法等。响应面法被Bucher等[5]首次应用于土木工程领域。之后各国学者采用该法对曲线工字梁钢梁、单跨砌体拱桥、多跨连续梁桥、隔震连续梁桥、混凝土拱坝等进行了易损性分析[5-12]。Li等[13]提出了一种改进的均匀设计-响应面模型方法对桥梁构件及系统进行易损性分析。Xiao等[14]基于改进的响应面方法,完成了对结构的易损性分析。吴文朋等[15]分析了不确定因素联合效应对桥梁易损性的影响。Li等[16]通过易损性分析发现近断层地震作用下钢筋混凝土桥梁失效概率较远场地震动明显更高。钟剑等[17]通过蒙特卡洛法对钢筋混凝土连续梁桥进行易损性研究,结果表明,构件相关性对桥梁易损性分析结果的误差影响大。

在地震风险分析方面,Chan等[18]采用全寿命分析法分析美国10条高速路段的成本及维护费用;Kong等[19]提出劣化结构全寿命维护成本评估方法;Wang等[20]分析钢桥全寿命周期成本模型,环境成本作为其间接成本;党育等[21]提出将建筑预期损失与全寿命费用之比作为指标,对比隔震和非隔震结构抗震性能;林政园等[22]研究基于桥梁耐久性和安全性的恢复时间功能函数。综上所述,国内外学者采用不同的分析方法对各类桥梁结构进行了地震风险分析,研究成果较丰硕,然而对高铁摩擦摆隔震桥梁结构所面临的地震风险则了解得不够透彻。

本文基于响应面法,考虑结构和地震动的不确定性,以位移延性比、剪切变形分别作为墩柱和支座的评价指标,对比高铁桥梁隔震前、后墩柱和支座的易损性曲线,以及隔震和非隔震高铁桥梁的经济损失和全寿命费用,深入了解高铁隔震桥梁的地震风险。

1 基于响应面法的高铁隔震桥梁地震易损性分析方法

1.1 响应面函数的确定

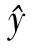
选择office 2010Excel软件录入并进行分析，应用SPSS 21.00软件进行数据分析，计数数据采用百分比表示，计量数据采用均数±标准差表示，计数数据与计量数据对比方法主要为t检验与卡方χ2分析，P<0.05为差异显著。

(1)

式中:k为不确定因素个数;xi、xj为结构设计变量,如PGA或结构强度等参数;a0、ai、aij为待定系数;ε为拟合误差,服从正态分布。

响应面法的关键一环是选择合理的试验设计方法。其中,中心复合设计方法由于具有高效、灵活及试验数合理等优点得到了广泛应用,本文采用该法开展试验设计,需要确定的试验点数为2k+2k+1个,包括1个中心点,2k个轴线点和2k个象限点。对试验样本进行非线性分析得到响应值,通过最小二乘法回归确定待定参数,进而得到地震动强度-结构响应值,即响应面函数。

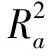
R2=A/B,

(2)

A=αTXTY-(ITY)2/N,

(3)

B=YTY-(ITY)2/N,

(4)

(5)

表5中,试验点号1～25代表中心复合设计的25组试验。由以上试验数据可以得到各构件地震响应平均值μ和标准差σ的拟合多项式响应面函数,函数中的未知参数通过最小二乘法拟合确定。隔震桥墩损伤指标的平均值和标准差响应面函数如下:

1.2 构件损伤指标

支座和墩柱作为隔震桥梁的主要竖向受力构件,在地震作用下若出现损伤或破坏,不仅导致其自身的性能发生退化,而且可能危及整座桥梁的安全性,故需要定义其损伤指标及判别准则,以便分析其损伤情况。本文选取位移延性系数[23]作为桥墩的损伤判别指标:

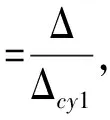
(6)

式中,Δ、Δcy1分别为地震下桥墩墩顶最大位移和首次屈服位移。桥墩损伤破坏一般划分为5个等级:基本完好λ≤1,轻微破坏1<λ≤1.232,中等破坏1.232<λ≤3.011,严重破坏3.011<λ≤6.011,完全破坏λ>6.011。

通过SAP2000建立高铁桥梁有限元模型,非隔震和隔震结构分别采用盆式支座和摩擦摆隔震支座。桥墩混凝土和钢筋分别采用Mander本构模型和双折线本构模型。摩擦摆支座采用Friction Isolator连接单元,主梁采用弹性梁柱单元。采用PMM纤维铰单元来模拟桥墩的塑性转动能力。高铁隔震桥梁的有限元模型如图1所示。

对于摩擦摆支座及盆式橡胶支座,其在遭受地震作用下能通过剪切变形来延长结构周期和耗散地震能量,但若其剪切位移大于支座的设计位移时将会发生剪切破坏导致支座失效,参考了相关文献[24-27]的相关规定后,本文选取支座剪切位移D作为其损伤判别指标。将设计位移D作为轻微破坏的阈值,本文取200 mm,支座损伤等级划分标准见表1,借鉴公路桥梁的划分标准,结合相关文献[28]定义其损伤等级。

表1 支座损伤等级划分标准

1.3 结构-地震动样本不确定性及随机参数归一化

以PGA 为地震动输入变量,并考虑其不确定性是目前的常见做法[29]。在结构的不确定性方面,考虑到高铁桥梁建造过程中环境和施工技术等因素的影响而导致自身具有很大的不确定性,因此,选取钢筋弹性模量Es、屈服强度fy及混凝土抗压强度fc这些主要影响因素作为结构的随机参数,它们均符合对数正态分布。

从行政权的历史发展来看，通过政府等公共组织载体行使的行政权力都是基于公共需要和公共利益而产生，目的是避免私利对公共利益的侵蚀。现代公共行政理论更加强化政府管理的公共属性，将政府视为公共利益的代言人，并将政府行为的价值取向等同于社会公共利益的现实需求。网约车涉及的公共利益并不是网约车车主或网约车公司经营者的利益，也不是传统出租车经营者的利益，而是整个民众出行团体的整体利益，网约车的管理效果决定了政府在互联网+和互联网-之间如何选择的问题。

由上节得到的桥墩和支座各级破坏状态的超越概率,根据文献[30]给出的地震脆弱性定义以及公式,将上节易损性分析数据代入式(10),得到不同破坏状态的发生概率。限于篇幅,图7给出非隔震和隔震边墩各级损伤状态的发生概率。

(7)

式中,xi=1、0、-1分别代表ξi取最大值、最大与最小值的平均值及最小值。

1.4 基于响应面法的地震易损性分析

在得到构件地震响应平均值与标准差的响应面函数后,就可以对高铁隔震桥梁进行地震易损性分析。采用拉丁超立方法(Latin Hypercube Sampling,LHS)抽取并建立若干个桥梁-地震动样本对,将样本对的随机参数fy(x1)、Es(x2)、fc(x3)及PGA代入响应面函数,判断结构所处的破坏状态,即可得到相应损伤指标的概率分布及每个破坏等级的超越概率,重复以上步骤得到易损性曲线:

(8)

式中,Pf为在地震作用下结构达到或超过某种破坏状态的失效概率;M为桥梁-地震动样本对的个数;N(u≥LSi)为结构响应达到或超过指定极限状态的次数。

2 高铁隔震桥梁响应面模型

2.1 高铁隔震桥梁有限元模型

以某典型摩擦摆隔震高铁简支梁桥为研究对象,共6跨,每跨32 m,桥墩高度均为22 m,采用双线圆端形实体桥墩,混凝土C35。主梁采用C50混凝土,相邻主梁间距10 m。8度地震区,场地特征周期为0.45 s,PGA为0.3 g。

老福说：“行了行了，坐下吧，既然来了，咱们好好聊聊，你们说呢？”他嘱咐母亲去给他们沏壶茶，母亲不情愿地照办了。

本文所采用的摩擦摆支座主要性能参数如下:支座的滑动曲率半径为1.5 m,摩擦系数为0.03,竖向设计承载力为5 000 kN,设计极限位移为200 mm。

陈洋依旧用不紧不慢的语调说：“什么样的凶手永远不会被人抓住？当然是死了的人。只需要收买抢救的医生，换一具被解剖过的残尸，杜朗就可以明正言顺地死了。而一个死人去杀人，留下一堆指纹又能怎么样呢？”

图1 高铁隔震桥梁有限元分析模型

2.2 响应面函数模型的建立

本例中,选取钢筋屈服强度fy、弹性模量Es以及混凝土的抗压强度fc为结构参数输入变量,其分布类型见表2。另外选取PGA作为地震波输入变量从而模拟地震波的不确定性,4个参数归一化后的均值见表3。

表2 结构参数输入变量的分布

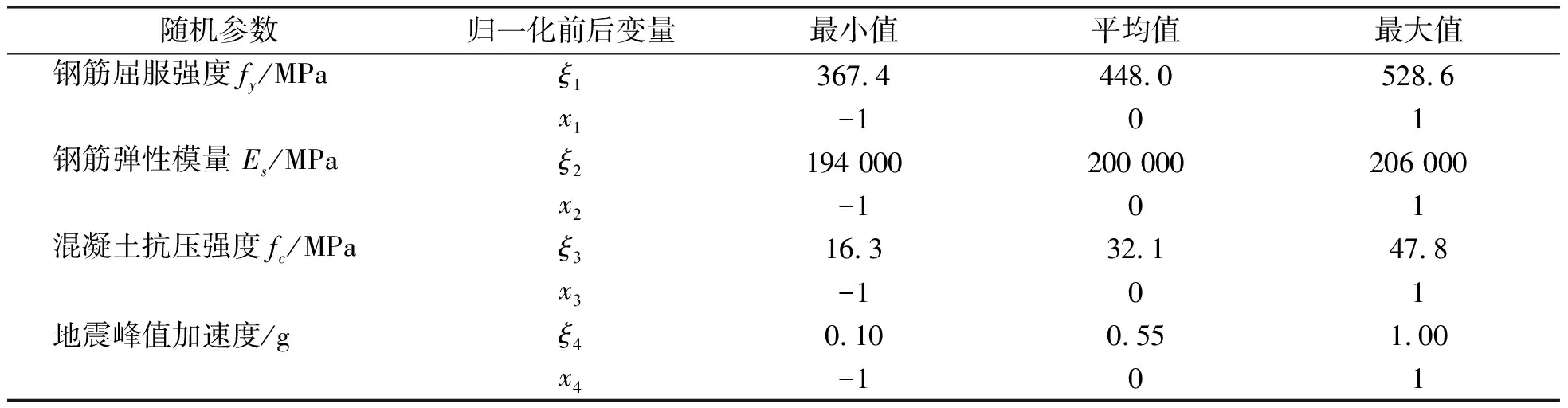
表3 随机参数及其归一化

式中,P[Di|Ij]为构件震害矩阵,P[Ij]为烈度发生概率。

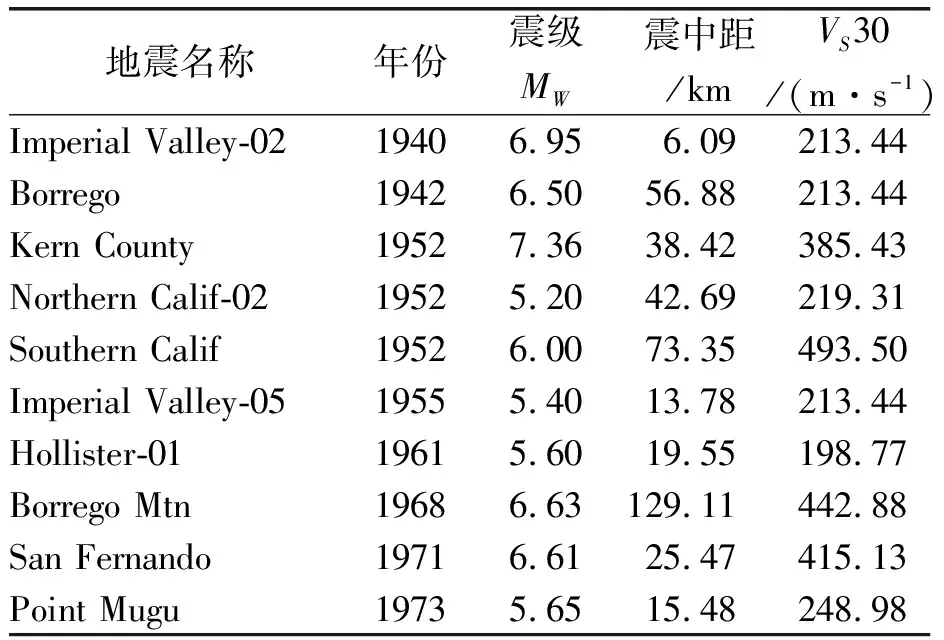
表4 地震波信息

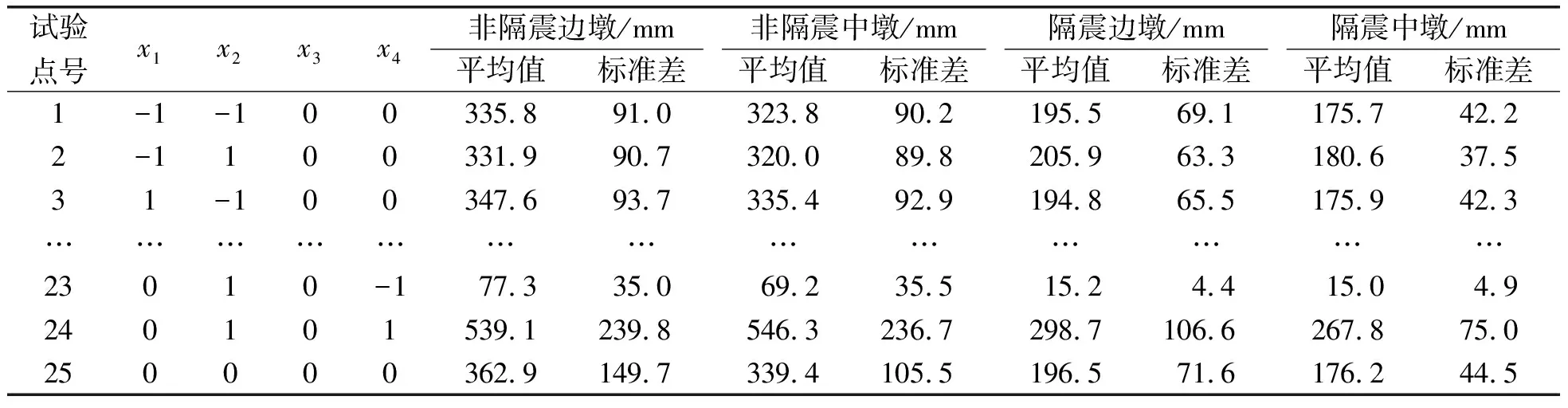
表5 非隔震与隔震高铁桥梁墩顶位移

式中,α为待定参数,X、Y分别为设计变量矩阵和真实响应向量,I为单位向量,N为样本数量。

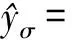
(9)

4个随机参数对隔震与非隔震桥梁墩顶位移及支座剪切位移影响的响应等高线与响应曲面如图2,限于篇幅,只列出钢筋屈服强度fy和钢筋弹性模量Es对隔震与非隔震桥梁边墩墩顶位移影响的响应曲面。

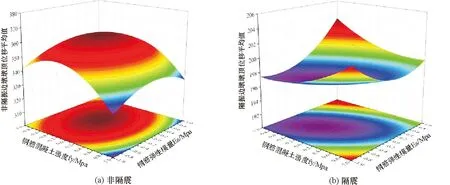
图2 钢筋屈服强度和弹性模量对非隔震与隔震高铁桥梁边墩墩顶位移的影响

2.3 响应面模型准确性检验

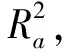
新常态的背景下，传统理念下连锁零售业实体企业所推行的经营模式，已经不能适应社会主义现代化的需求。那么，在电商冲击下的连锁零售业实体企业经营模式就开始略显落后，竞争形式也展现了单一的境界。还有部分连锁零售业实体企业经营模式是“重销售，轻服务”。甚至还有的把“关注+了解+购买”作为销售理念，进行销售活动［4］。这样不仅不能为消费者提供个性化的服务，而且长时间状态下的不主动与消费者进行交流，就难以激发消费者的购买欲望。在此种情况下，若长久下去，就会严重影响连锁零售业实体企业经营模式的有效延伸。

表6 非隔震与隔震高铁桥梁桥墩与支座响应面拟合系数

3 隔震与非隔震高铁桥梁构件易损性对比

3.1 隔震与非隔震高铁桥梁桥墩地震易损性

依据前述方法,建立1 000个桥梁-地震动样本对带入响应面函数来计算易损性曲线。隔震与非隔震高铁桥梁墩柱位移延性系数的地震易损性曲线,及其在各级破坏状态下的对比如图3和图4所示。

通过安装预应力波纹管（见图2），可以对孔道进行保护，防止预应力钢筋束在穿束过程中对混凝土结构造成损坏。固定塑料波纹管时，应先在箍筋上确定预应力曲线的具体的位置，然后通过钢筋马凳进行支托，间隔为700mm，然后通过焊接将支托的钢筋固定在箍筋上。为了保证塑料波纹管的施工的效果，避免在浇筑混凝土的过程中产生偏移，塑料波纹管和支托的钢筋的固定必须牢固。

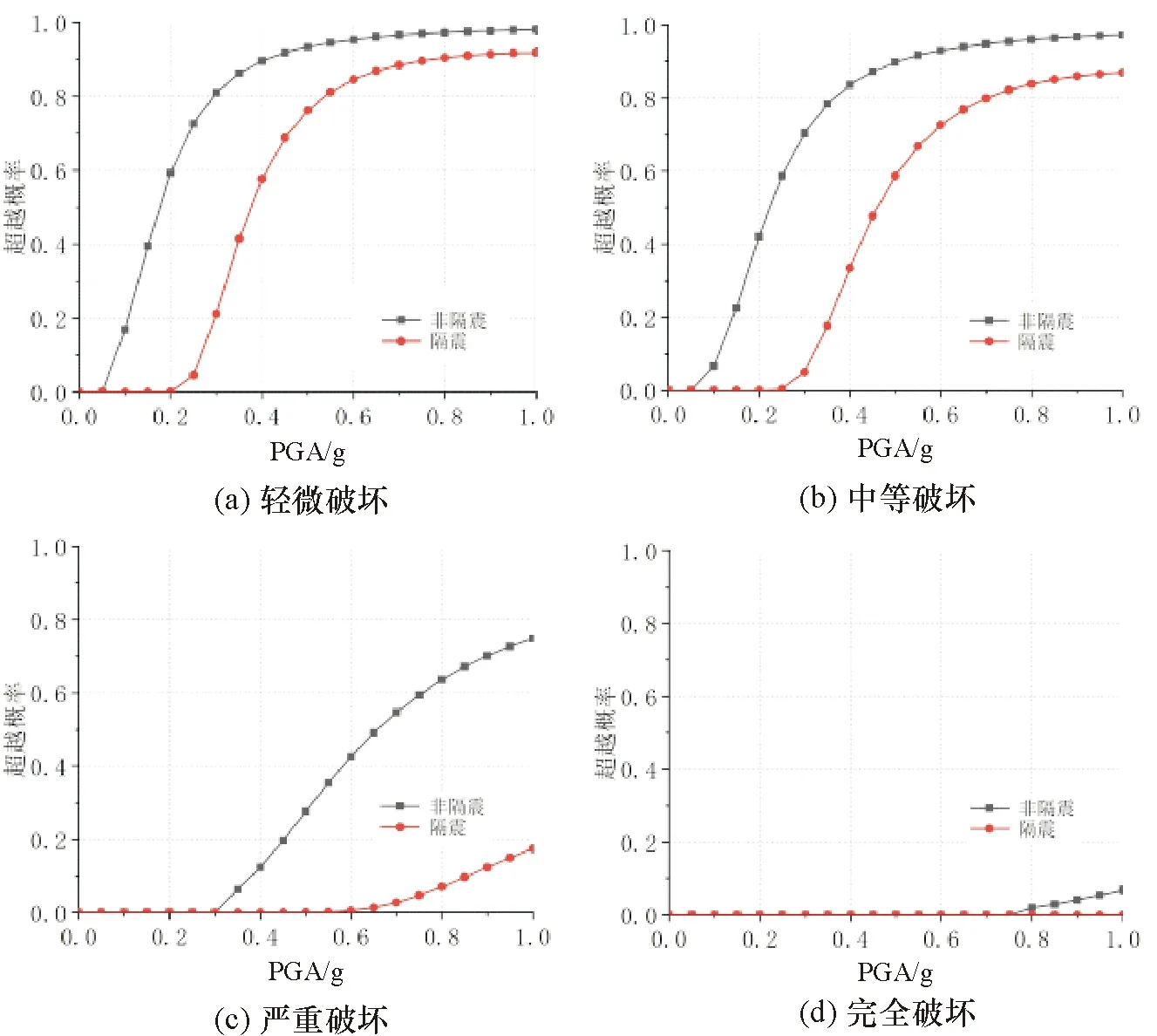
图3 隔震与非隔震高铁桥梁边墩易损性曲线对比

图4 隔震与非隔震高铁桥梁中墩易损性曲线对比

由图3～图4可知,地震动加速度峰值越大,结构构件的累积损伤超越概率越大;从轻微破坏到完全破坏,隔震与非隔震桥墩超越概率均逐渐减小;隔震桥墩各级损伤状态的超越概率均明显小于非隔震桥墩:在罕遇地震PGA为0.57 g时,隔震与非隔震桥梁中墩出现严重破坏的超越概率分别接近0和27.6%;当PGA达到1.0 g时,隔震和非隔震桥梁中墩出现完全破坏的超越概率分别为0和6.1%。以上数据说明隔震支座能明显降低高铁桥梁墩柱在地震中的损伤程度,有效保护高铁桥梁的安全性。

3.2 隔震与非隔震高铁桥梁支座地震易损性

各级破坏状态下,隔震与非隔震高铁桥梁边墩支座以及中墩支座的剪切位移的地震易损性曲线分别见图5和图6。

烈度与加速度之间的换算关系为

图5 隔震与非隔震高铁桥梁边墩支座易损性曲线对比

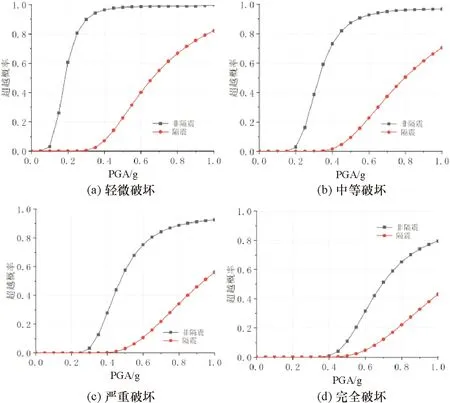
图6 隔震与非隔震高铁桥梁中墩支座易损性曲线对比

由图5～图6可知,中墩与边墩支座同一损伤状态的变化规律类似;从轻微破坏到完全破坏,相同地震动对应的支座超越概率逐渐变小;无论何种损伤状态,隔震支座的超越概率比非隔震支座小:当PGA等于0.57 g 时,桥梁中墩的非隔震和隔震支座严重破坏的超越概率分别为70.9%和6.3%,而完全破坏的超越概率分别为26.7%和3.0%,说明隔震支座超越严重破坏以及完全破坏的概率远低于非隔震支座。

4 高铁隔震桥地震风险分析

4.1 结构的震害矩阵

采用中心复合设计法对变量进行试验设计时,应使其尽量包含于随机区域[μ-3σ,μ+3σ]内。为了加快运算速度并提高拟合效果,对各随机参数进行归一化处理,ξ1～ξ4分别代表fy、Es、fc及PGA这4个随机参数,x1～x4分别代表4个随机参数归一化值。

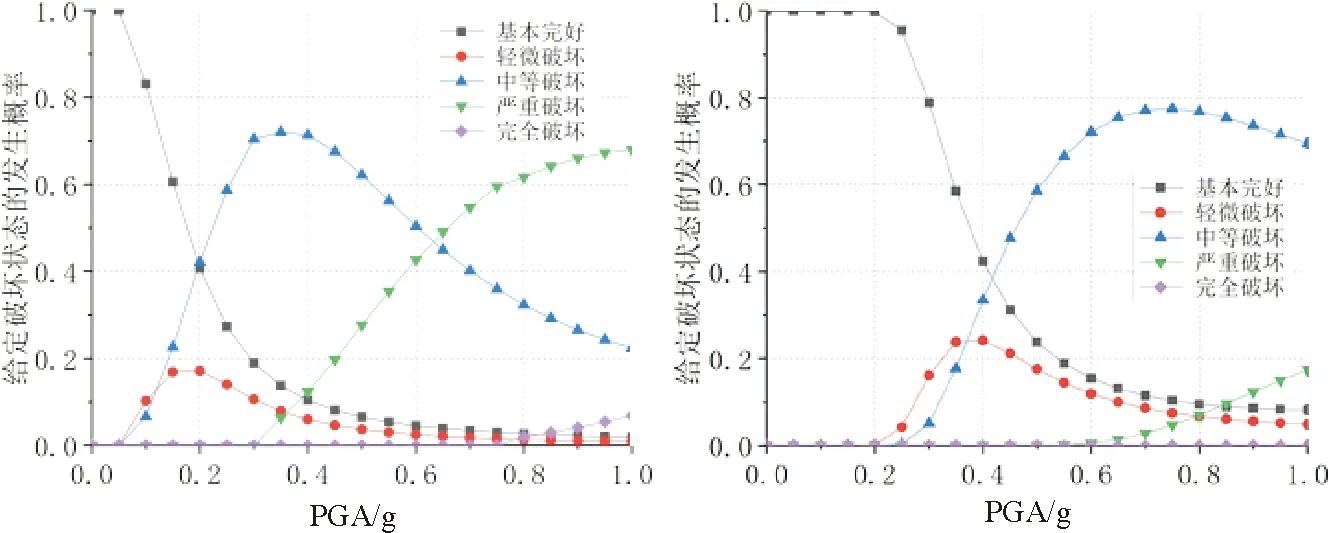
图7 非隔震与隔震桥梁边墩墩柱各级破坏状态发生概率

(10)

式中,PDFi为各级破坏状态的发生概率,i为破坏等级。

我们注意到，很多学者论及语言符号的任意性时，都沿用了索绪尔本人举过的例子，从未怀疑过这些例子有没有问题，例如：

Amax=10(Ilg2-0.104 757 5),

(11)

式中,Amax为地震峰值加速度,I为基本烈度。

根据公式(11)的换算关系以及响应发生概率曲线,可得到隔震和非隔震高铁桥梁桥墩和支座的震害矩阵(表7)。限于篇幅,只给出非隔震、隔震边墩墩柱的震害矩阵。可见,非隔震桥墩发生严重破坏和完全破坏的概率远高于隔震桥墩。

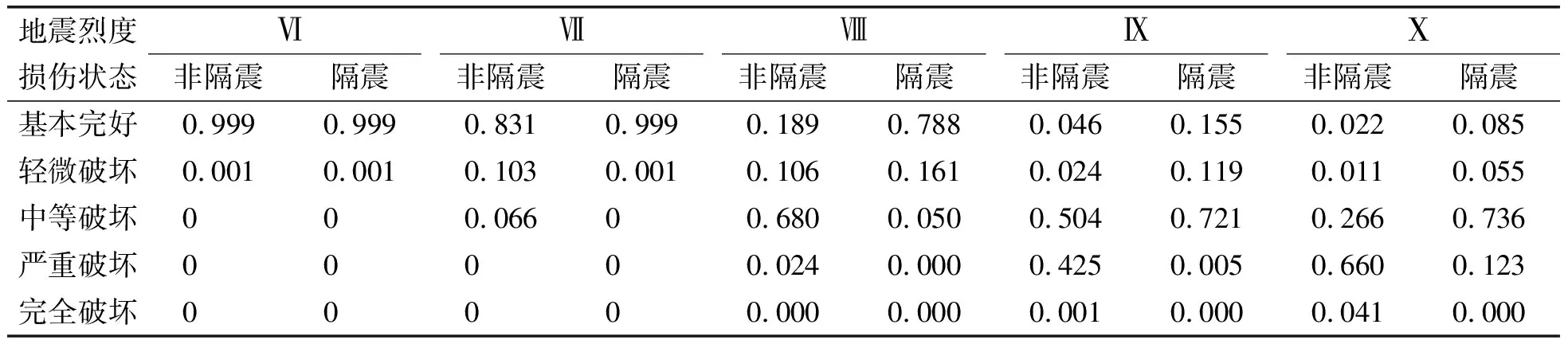
表7 隔震、非隔震高铁桥梁边墩墩柱的震害矩阵

4.2 地震损失分析

基于震害矩阵,构件在服役周期内不同破坏状态下的损伤概率Pf[Di]为

(12)

高铁桥梁横桥向刚度大,不易破坏,因此,本文分析仅考虑纵桥向地震动输入。根据目标反应谱选取10条符合条件的天然地震波,10条天然波的具体信息见表4,按照0.05 g的间隔在0.1～1.0 g范围内逐渐增大。本算例随机变量k=4,因此,试验点数为25个。利用SAP2000对25组试验样本在10条地震波下进行250次非线性动力时程分析。假定墩柱和隔震支座的响应都服从正态分布,所以25组试验下墩柱或支座的响应平均值和标准差就构成每一试验点下的响应面模型。非隔震和隔震高铁桥梁墩柱墩顶位移地震响应如表5,支座最大剪切变形等响应结果限于篇幅,不再赘述。

地震造成的经济损失主要包括直接和间接经济损失,以及抗震救灾投入费用3部分。在服役期内遭受各种可能地震烈度时,结构破坏造成的直接经济损失可由破坏状态的损伤概率求得:

我咕咚咕咚一仰脖喝完了那碗开水。我觉得这个地方不适合我久呆。我想，小六子的爹一定是把命丢在西山了。难怪在我没来的时候，就有人称西山为鬼门关呢。

(13)

式中,l(Di)为结构各级状态对应的损失比,铁路桥梁5个破坏等级对应的损失比分别为10%、20%、40%、70%和100%[9];CI指高铁桥梁初始造价[20]。

由于间接经济损失计算的复杂性,本研究中暂不考虑。根据《地震现场工作大纲和技术指南》[31],救灾投入费用等于直接经济损失乘以一定的比例系数,6度以下、6～7度及7度以上地震,比例系数分别取1.5%、3.5%和6%。

4.3 全寿命费用分析

结构全寿命费用包含整个寿命周期内的初始造价、损失费用及检修维护费用:

CLCC=CI+CM+CL,

(14)

式中,CI、CM、CL分别指桥梁初始造价、检修费用和地震损失。检修维护费用一般等于初始造价乘以检修系数,非隔震、隔震高铁桥梁检修系数分别等于5%和4%。基于前文的分析结果,高铁隔震及非隔震桥梁的全寿命费用如表8所示。

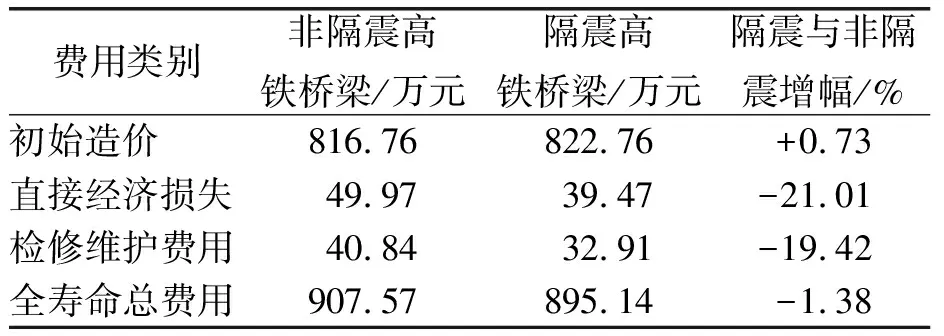
表8 高铁桥梁全寿命费用分析

由表8可见,与非隔震桥梁相比,隔震桥梁的直接经济损失费用、救灾投入费用及检修费用均明显降低,平均减少20%左右,说明隔震技术可有效降低结构的地震损失,减少救灾和维护费用。尽管隔震桥梁的初始造价比非隔震结构增加了0.73%,但从全寿命周期总费用来看,隔震结构仍然比非隔震结构费用降低。

一般亩施充分腐熟的鸡粪或羊粪1500-2000 kg，方法是在垄间均匀撒施。另外亩施复合肥80 kg，集中沟施在播种沟一边未深翻处作基肥。

在高速公路隧道施工过程中通常会采用钢支撑施工技术。在使用这种技术之前，施工人员必须要对隧道的断面形式和具体地质情况要开展反复的、认真的检测。如果施工人员对隧道施工图纸中的数据或者信息不清楚，施工人员机械操作不当导致对隧道的挖掘深度不足或者过大，这样的话就需要对挖掘的平面重新进行施工处理，使得隧道平面质量能够达到施工质量的规定要求。在对隧道平面的施工质量进行验收合格完毕后，要尽可能在短时间内开展混泥土的喷射工作，同时还要开展钢架的支撑工作。钢架的支撑将为施工安全提供相应的技术保障。

5 结 论

本文将响应面法运用于高铁隔震桥梁地震易损性分析中,目的是减少模型的计算量,提高计算效率。结论如下:

(1)采用响应面法分析高铁桥梁的易损性,可通过较少的非线性分析(本例250次)得到结构响应面函数,进而可以分析数倍的样本响应(本例1 000个),说明该法极大地提高了计算效率。

(2)隔震桥梁桥墩各级破坏状态的超越概率明显小于非隔震桥梁,说明隔震桥梁在地震中能得到有效的保护,不易发生破坏。与隔震支座相比,非隔震支座在各级损伤状态下的超越概率明显更高,说明非隔震支座在地震作用下可能会产生较为严重的损伤。

据了解，《安徽省淮河流域综合治理规划纲要》期限为2011—2020年，重大项目展望至2030年及以后，规划区涉及10个省辖市的52个县区，2010年人口规模为4035万人，占全省的59%。规划提出，要以防洪保安、供水保障、生态保护为重点，加快推进淮河流域防洪、防旱、防污、供水综合治理，到2020年，基本建成与城镇化、工业化、农业现代化“三化同步”相适应的综合水利工程和水资源保障体系。

(3)隔震桥梁的直接经济损失、救灾投入费用及检修费用均明显小于非隔震结构,说明隔震技术能够有效降低地震所造成的损失。从全寿命总费用角度看,隔震桥梁的全寿命总费用相对于非隔震桥梁有所减少,说明隔震桥梁具有较好的经济性。