一种改进GPU加速策略在光滑粒子流体动力学方法中的应用

管延敏, 杨彩虹, 康 庄, 周 利

(1. 江苏科技大学 船舶与海洋工程学院,江苏 镇江 212003;2. 哈尔滨工程大学 船舶工程学院,哈尔滨 150001)

光滑粒子流体动力学(Smoothed Particle Hydrodynamics,SPH)对模拟自由表面流动问题具有先天优势,但随着粒子数量的增加,尤其是三维流动问题,计算效率急剧降低,极大限制了该方法在大规模计算中的适用性.利用图形处理器(GPU)众核架构开展多核并行计算的计算机统一设备架构(CUDA)技术,其强大的并行特性非常适合解决大规模的高级计算问题[1],尤其是计算密集型问题.SPH计算能力密集的特性使其能容易地在GPU上实现并行运算,因此一些学者开始尝试将GPU技术应用于SPH方法.Harada等[2]首次描述了SPH方法在GPU上的实现,Crespo等[3]将GPU加速的SPH方法应用于模拟复杂的自由表面流动.他们的研究均表明在单个GPU上的SPH模拟比在单核中央处理器(CPU)上进行的SPH模拟要快两个数量级.目前SPH方法在GPU平台下的计算研究发展迅速,GPU加速的SPH模型已应用于颗粒流体流动的模拟和浅水方程的求解[4-5],并通过结合自适应粒子技术[6]实现了高效计算.国内,徐锋[7]在实现了基于GPU众核架构的并行SPH算法的同时,结合所使用的GPU硬件上的特点,对并行算法进行了优化,将计算效率提高了20倍以上;金善勤等[8]提出一种基于粒子对的并行计算方法并将其与改进的SPH方法结合,实现了超过10的加速比;杨志国等[9]将GPU算法应用于二维溃坝模拟中也获得了数量级的加速效果.

但是,GPU的系统设计理念与CPU正好相反,GPU面对的是类型一致、互不关联的大量数据,其显存的读写对算法求解效率影响很大.随着流场的不断演变,SPH粒子的无序化很容易导致多个线程同时读写同一地址而引起访问冲突,极大地影响了计算效率的稳定性.针对此问题,并行索引排序方法[3, 10]、Z索引排序方法[11]及其改进方法[12]相继被提出,这些方法通过优化SPH粒子索引存储方式使同单元粒子在GPU显存中尽可能相邻,一定程度上改善了GPU显存访问的不连续问题,但没有从实质上改变单元粒子的无序化.为此,本文提出了一种粒子重新编号技术,实现了SPH粒子的有序排列和GPU显存的连续访问,并将该方法应用于三维带障碍物溃坝模拟,通过与实验数据比较以及不同硬件设施上不同算法求解效率的对比,验证了本文方法的精确性和高效性.

1 SPH的控制方程

SPH控制方程的离散形式可表示为

(1)

(2)

式中:ρi、pi、ui、Vj分别为流体粒子i的密度、压力、速度和体积;t为时间;mj和ρj为粒子i支持域中粒子j的质量和密度;g为重力加速度;Wij为核函数,本文采用Wendland[13]的C2核函数:

(3)

(0≤q≤2)

式中:r为两粒子间距离;h为光滑长度;q为粒子间相对距离,q=r/h;αd为常数,对于三维问题,αd=21/8πh3.

人工黏性为

(4)

式中:

(5)

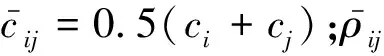
假定流体弱可压缩,采用Monaghan等[14]提出的人工压缩法求解压强:

(6)

2 CUDA-GPU架构下的SPH模型

2.1 并行算法的实现流程

针对现代CUDA-GPU架构设计了一种高效的SPH流体数据,以提高SPH流体模拟在GPU上的数据处理速度.并行代码使用C#语言和CUDA编程语言进行开发,大多数源代码都是CPU和GPU所共有的,可以在CPU或GPU上执行,也可以在没有启用GPU的工作站上运行,只使用CPU实现.并行算法实现的流程如图1所示,粒子信息的初始数据存储在CPU中,将数据传输到GPU中之后,后续的所有计算都在GPU中进行,即所有涉及粒子循环的任务执行都是由GPU的并行结构来完成的.在完成控制方程求解和粒子物理量更新之后,将更新后的粒子物理量从GPU再次传输到CPU进行保存和输出.

图1 SPH并行算法的实现流程Fig.1 Parallel arithmetic mode of SPH

2.2 粒子搜索

SPH方法由于核函数的紧支性,只有粒子支持域内的相邻粒子才会相互作用,因粒子间的相对位置不断变化,每个时刻都需要进行最近相邻粒子的搜索,所以搜索算法极大地影响着SPH的计算效率.本文采用Monahan[15]的链表搜索算法,通过使用控制网格搜索粒子的相邻质点.其主要思想为:在计算域建立临时网格,网格大小和粒子支持域大小一致,然后建立每个粒子与所处网格的关联形成关联链表.对于三维问题,计算域被划分为立方单元,每个单元与其周围的单元(共27个)组成紧邻单元,如图2所示.粒子根据它们在区域中的位置被放置在单元格中,在搜索粒子时只需搜索粒子所在的紧邻单元即可,形成最近相邻粒子对.

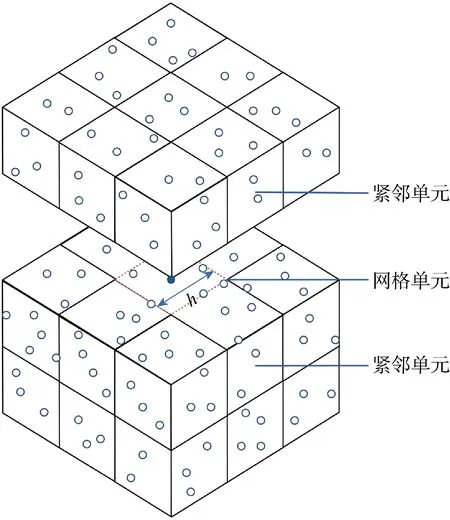
图2 三维相邻粒子链表搜索法示意图Fig.2 Sketch for three-dimensional neighbor list search method

2.3 粒子重新编号技术

邻近粒子搜索的GPU并行算法的构建与在CPU上使用的过程有所不同,在GPU上需要建立线程与粒子之间的关联,并为每个粒子单独分配一个计算线程.所有粒子按编号排入一个连续的标签数组,并给固定数目的连续粒子分配一个线程块.在流场模拟过程中,随着时间步不断推进,SPH粒子分布与初始粒子分布差异越来越大,链表搜索法中SPH粒子不再是顺序分布,如图3(a)所示,这就导致线程结束并行访问内存时,极易导致多个线程同时对同一内存地址进行读写操作而产生访问冲突,降低并行算法的求解效率.为保证算法效率稳定性,提出了一种粒子重新编号方法,图3显示了用于生成按单元格重新编号法的粒子标签数组简单示意图.

图3 粒子重新编号算法示例Fig.3 Example of neighbor list reorder

该方法主要包含以下步骤:

(1) 遍历所有SPH粒子,计算每个粒子所在网格索引,统计该索引所在网格存储SPH粒子数量,存储于数组IDCount中.

(2) 创建数组IDBegin,记录新粒子编号中每个网格中首粒子编号,对于网格m有IDBegin[m] = IDBegin[m-1] + IDCount[m-1];

(3) 清空数组IDCount;

(4) 遍历所有SPH粒子,重新统计该索引所在网格存储SPH粒子数量,根据粒子所在网格索引,对其重新编号,如对于某SPH粒子,其对于网格索引为n,其新的粒子编号为IDBegin[n] + IDCount[n],其中IDCount[n]为统计至该粒子时网格n中存储的SPH粒子数量,最终得到的重新粒子编号效果如图3(b)所示.

3 结果验证与分析

以SPH法验证自由表面流动问题的基准测试案例——溃坝问题为研究对象,对三维带障碍物的溃坝进行数值模拟,通过与实验数据进行对比验证本文并行算法的可靠性和有效性.

3.1 溃坝模型

荷兰海洋研究所(Marin)的溃坝试验[16]被广泛认为是验证SPH自由表面流动的基准算例.试验包含一个溃坝流与障碍物的碰撞,如图4所示.水箱长3.22 m、宽1 m、高1 m,水柱被储存在水箱一端,长1.228 m、宽1 m、高0.55 m,并在试验开始瞬间释放.障碍物设置在水流下游,随着挡水墙的拆除,由于重力作用,流体逐渐淹没水箱干床并与障碍物发生碰撞.试验通过设置3个垂直高度探头(H1、H2和H3)测量不同位置的水深,具体位置如图4所示.

图4 试验配置和试验数据的测量位置(m)Fig.4 Experimental configuration and measurement position of experimental data (m)

3.2 结果对比

数值模拟选取初始粒子间距为0.01 m、流场实粒子总数为 676 500,时间步长为0.1 ms.为验证本文粒子重新编号方法的准确性,对不同位置处的水深展开比较研究.图5所示为 H1、H2和H3位置处不同时刻的水深粒子重新编号前后计算值和实验值的比较.图中:hw为水柱高度.可见粒子重新编号前后计算值基本一致,不会对精度造成影响;在初始水柱中间(H3)、箱体中部(H2)、障碍物前缘附近(H1),本文计算值与实验值的趋势和大小都很接近.图中H3探头清晰地再现了溃坝的整个过程,在最初的2 s内水柱坍塌,相应地,这段时间的水位也不断下降,而在其他探头中,水流依次到达H2和H1.在1.75 s后,反射的水波撞击左墙后反向移动,第2次撞击障碍物以及右墙,同时,水深达到第2个峰值(H1的水深峰值时刻大概为4.8 s,H2为 4.6 s,H3为3.8 s).本文计算的水深与实验水深随时间的变化趋势大致相同,表明本文方法具有良好的计算精度.

图5 实验测量和本文模拟的探测点处的垂直水柱高度比较Fig.5 Comparation of vertical water heights at the detection point measured experimentally and simulated in this paper

4 效率测试结果与分析

4.1 测试平台

通过比较CPU串行、CPU并行、GPU并行SPH算法三维带障碍物溃坝数值模拟计算耗时,验证本文所采用GPU算法求解效率.为保证计算结果的适用性,分别在不同的CPU、GPU硬件上运行SPH算法,具体配置如表1所示.

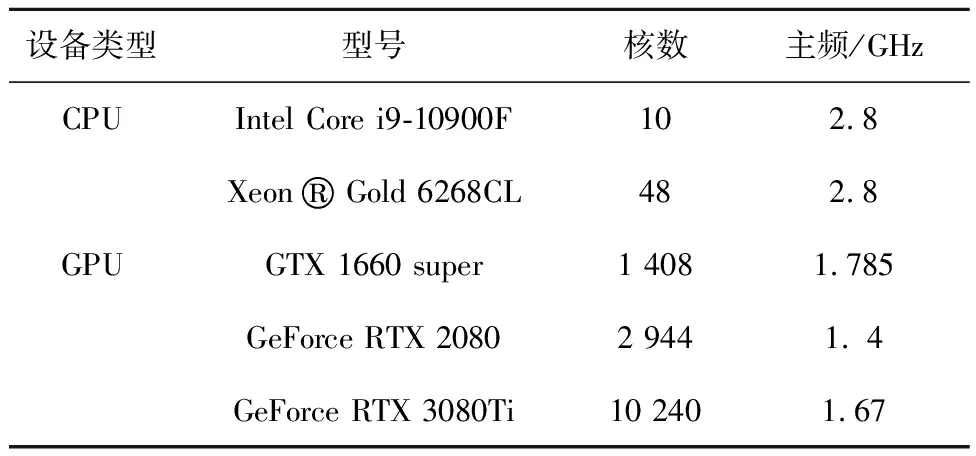
表1 CPU和GPU配置Tab.1 Hardware configurations of CPU and GPU

4.2 GPU算法粒子重新编号效果对比

图6为实粒子总数676 500时不同硬件条件下粒子重新编号和未重新编号GPU加速SPH算法单步运行时间(ts)对比.图中:sn为计算步数.由图可见,本文采用的粒子重新编号算法在不同硬件上都获得了稳定的单步运行时间,而粒子未重新编号时,随着流场中粒子的无序化导致GPU显存访问冲突,其单步运行时间呈对数增长,算例表明本文所采用的粒子重新编号方法可以保证稳定的单步运行时间,是有效的.

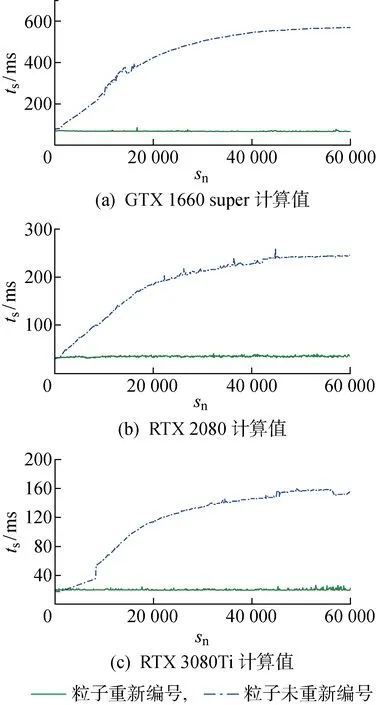
图6 粒子重新编号和未重新编号单步运行时间对比Fig.6 Comparison of step running time between reorder and non-reorder method

4.3 算法求解效率对比

图7为实粒子数为676 500时CPU并行和GPU并行算法迭代60 000步单步运行时间对比,可见GPU并行算法都有良好的计算效率,而求解效率稳定性弱于CPU并行算法.受SPH方法部分算法、函数间存在串行关系影响,计算效率未能随核数增加而线性增加,以Intel Core i9-10900F为参照,各硬件核数、效率比如表2所示,可见相对计算成本(核数效率比)随核数的增加而增大.图8为不同实粒子数下CPU并行、GPU并行SPH算法单步平均用时(tm)对比.图中:np为实粒子数.可见随着粒子数量的增加,CPU并行算法运行时间显著增加, GPU并行算法大幅缩短计算时间的优势愈发明显.

表2 各硬件核数和效率比

图7 CPU并行和GPU算法单步运行时间对比Fig.7 Comparison of step running time between CPU parallel and GPU parallel

图8 不同实粒子总数下CPU与GPU运行时间的对比Fig.8 Comparison of running time between CPU and GPU at different number of particles

为进一步验证本文粒子重新编号算法的有效性,对不同实粒子数下GPU算法并行效率与开源软件DualSPHysics进行了对比,如图8(b)所示,可见同实粒子总数、同硬件设备条件下,本文方法平均单步运行时间均小于DualSPHysics软件,算例表明本文粒子重新编号方法具有良好的效率优势.

5 结论

运用粒子重新编号技术开发了一套高效GPU-SPH并行算法,将该算法应用于三维带障碍物溃坝问题,并对算法求解效率进行了比较研究,得到以下结论:

(1) 粒子重新编号前后计算值基本一致,不会对精度造成影响,与试验值的对比表明本文所采用的方法精确有效.

(2) 粒子重新编号技术能够有效解决GPU-SPH算法中的显存访问冲突问题.

(3) GPU并行算法能够大幅提高SPH方法求解效率,随着粒子数量的增加,其大幅缩短计算时间的优势愈发明显.