矩形水平通道内液体Poiseuille-Rayleigh-Bénard对流的数值模拟

＊赵佳悦 侯红 梁启煜 郭永红

（山西能源学院 能源与动力工程系 山西 030600）

将封闭矩形通道内的水平液层从底部加热，表面冷却，再与层流强制对流叠加，这样的流动叫做Poiseuille-Rayleigh-Bénard（P-R-B）对流。Poiseuille-Rayleigh-Bénard对流广泛存在于自然界和工业领域中，例如化学气相沉积，电子设备冷却，海水淡化装置和板式换热器等。对Poiseuille-Rayleigh-Bénard对流的研究，有利于对换热器和材料制备过程进行合理设计和改良[1]。

流体在通道流动的过程中，由于浮升力的作用，会出现二次流。在一定范围的Re数下，液体的浮力引起纵向流卷（即流卷的轴线平行于流动方向）的发展。一些文献中通过理论计算，数值模拟或实验分析的方法研究了水平通道中的Poiseuille-Rayleigh-Bénard对流。Rahli[2]指出，Poiseuille-Rayleigh-Benard对流中，流动由两个对流源叠加而成：水平压力梯度引起的通道内主流和垂直温度梯度引起的二次流。文献[3-5]研究了底部加热，上面冷却的通道二次流的发生机制。纵向流卷在流动入口区域的侧壁附近触发，然后逐渐向中心移动，侧壁处的扰动是对流不稳定性形成的重要因素。Zhang[6]对底部和侧壁加热通道的流动和传热特性进行了实验研究，通道宽深比为6，其底部和侧壁被加热且通道顶部被冷却。实验结果表明，通道底部的热流密度一定时，液膜内部首先出现两个较大的流卷，并且占据整个横截面，之后增加到四个。Gau等[7]观察了两平行板之间空气的Poiseuille-Rayleigh-Bénard对流，运用流动可视化方法得出了Gr/Re2=20，Re=500条件下空气内部的流动状态。

研究发现，Poiseuille-Rayleigh-Bénard流动的流型和热传递取决于Ra数、Re数等参数[8]。Benderradji[9]对宽深比为10，底部均匀热流加热的水平通道内流体流动和传热特性进行了数值计算，得出当Ra/Re2＞18时纵向流卷产生的机理发生改变，而且有流卷产生时，整体的传热系数明显大于仅有强制流动的通道。Ostrach和Kamotani等[10]对等温板之间充分发展的气流进行了实验，指出涡卷在Re=38，Ra＞8000时变得不规则。Nicolas[11]通过实验方法做出了无限大宽深比和有限宽深比通道内Poiseuille层流流动中Ra-Re平面的稳定性图，确定了流动的临界Re数和Ra数。Ostrach和Kamotani发现在大宽深比的通道中，纵向流卷的波长大约等于液体高度的两倍，即使对于大Ra数的情况也是如此。

本文采用数值模拟的方法研究底部定温加热、表面定温冷却的矩形水平通道内液体的Poiseuille-Rayleigh-Bénard对流，分析不同Re数和Ra数对流型和换热的影响，为工程实践提供一定的理论依据。

1.物理数学模型

本课题采用的物理模型为矩形水平通道，如图1所示。其几何尺寸长为L=50cm，宽为W=10cm，深为d=1cm。上表面为冷却表面，温度为Tc，下表面为加热面，温度为Th，左右侧壁为绝热竖壁，流体以速度v流过通道，入口温度为T=Tc，环境温度T0=Tc。为简化起见，假定：（1）液体为不可压缩牛顿流体，密度满足Boussinesq近似；（2）所有固体壁面均为无滑移边界条件；（3）流动速度低，为层流。

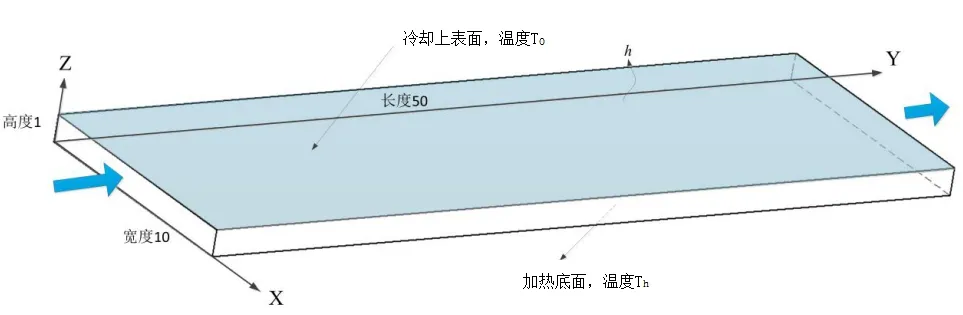
图1 物理模型

2.结果分析与讨论

（1）纵向流卷形成的机理。图2为当Re=10，Ra=5000时，不同的X-Z截面上的纵向流卷图。这种纵向流卷形成的机制，被称为经典机制。从图中可以看到，纵向流卷起初形成于两侧壁处（Y=5），并逐渐沿着流体流动方向往通道的中心区域扩展（Y=8，Y=15）。从Y=22之后，纵向流卷完全发展。这是因为在侧壁绝热情况下，由于速度边界层的存在，流体流动的速度沿通道中心向两侧壁逐渐减小。因此强制对流在侧壁附近较弱，在通道中心附近较强，可以认为流体在侧壁附近是自然对流，所以绝热侧壁附近的热量不容易散失，导致热量在侧壁面附近聚集，温度升高。因此，在通道内部形成了X方向温度梯度，由于流体密度随温度升高而降低，该处的温度梯度使流体产生了密度梯度。在侧壁附近的流体密度低于通道中心区域流体的密度，在浮升力和重力的作用下，侧壁附近流体向上方流动，而稍远离侧壁的流体向底部流动。同时，由于此处Z方向上亦存在温度梯度，因此，在通道两侧壁处的流体便会产生流卷。再加上流体内部,黏性力的作用，两侧壁处的流卷逐渐在其后方激发出新的流卷，直至流卷布满整个通道的X-Z截面。纵向流卷形成时在通道内成对出现，且相邻的两个流卷旋转方向相反。流卷直径约等于通道高度。在充分发展区，在X-Z截面上共有12个纵向流卷。

图2 Re=10, Ra=5000时不同X-Z截面上纵向流卷的温度场和速度场

（2）Re数对Poiseuille-Rayleigh-Bénard对流的影响。图3为Ra=5000时，Z=0.5截面上的无量纲温度场在不同Re数下的变化。可以看出，随着Re数的增加，充分发展区的纵向流卷出现位置逐渐向后移。这是因为在通道特征尺寸保持不变且流体黏度值基本稳定的情况下，Re数的增加意味着流体流速增加，从而在入口段相同Y坐标位置处的绝热侧壁附近的对流增强，热量不容易在侧壁聚集，因此纵向流卷在充分发展区的出现位置不断向后移动，但纵向流卷的个数不随Re数的改变而改变。

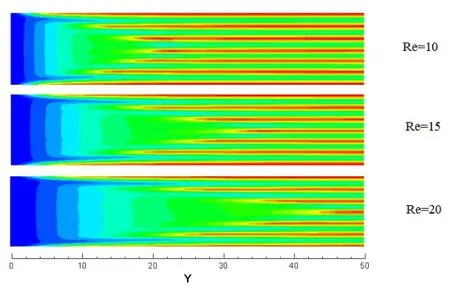
图3 Ra=5000时不同Re数下Z=0.5截面的温度云图

（3）Ra数对Poiseuille-Rayleigh-Bénard对流的影响。在流体力学中，Ra数是用来表征浮力驱动流体的无量纲数。当Ra数低于某个临界值时，流体内部的传热主要以导热的形式；当Ra数超过该临界值时，流体内部的传热主要是以对流形式。对于水平通道内液体的Poiseuille-Rayleigh-Bénard对流来说，研究Ra数对流体流动的影响是至关重要的。正如前文所提到的，水平矩形通道内的纵向流卷与流体内部温度梯度引起的浮升力有关。当封闭矩形通道内流体的Ra数小于使流卷出现的临界Ra数时，由该温度梯度产生的浮升力不足以克服流体内部的黏性力，从而无法触发纵向流卷，此时通道内为单纯的Poiseuille流动。在一定Re数下，当Ra数超过这个临界值，浮升力的影响逐渐增加，并能够克服流体黏性力的影响，使流体内部的热对流变得不稳定而激发出横向流卷。若Ra数继续增加，直到大于某值（即Ra*），同时使Re数大于Re*，这时通道内流动由横向流卷转变为纵向流卷。

图4为在Re=10时，不同Ra数下Z=0.5截面处的温度云图。可以看到，随着Ra数的增加，初始纵向流卷在侧壁附近形成的位置逐渐靠近入口区。在Ra=5000的时候，初始纵向流卷大致在Y=2.2处出现；当Ra数增加到12760时，初始纵向流卷大致在Y=1.7处出现；当Ra=22700的时候，初始纵向流卷大致在Y=0.8处出现。这主要是因为随着Ra数的增加，流体内部对流换热逐渐增强，从而使得侧壁附近能够激发出纵向流卷的温度梯度出现的位置逐渐靠前。从图中还可以看到，在Ra=5000的时候，充分发展区出现位置大致在Y=23处；而当Ra数增加到12760时，充分发展区的出现位置向前移到了Y=11处；当Ra=22700时，充分发展区的出现位置大致在Y=6.8处。这也就是说，随着Ra数的增加，矩形通道内流体的充分发展区出现位置距流卷开始形成位置的长度也逐渐变短。这是因为随着Ra数的增加，浮升力对流体的影响逐渐增强，从而使得纵向流卷向中心区域扩展的速度增加。当Ra=5000时，充分发展区通道截面上的纵向流卷数量为12个；当Ra=12760时，该区域的纵向流卷数量增加到14个；当Ra=22700时，纵向流卷数量为16个。而且可以看出，截面处的流体温度随着Ra数的增加升高得更快。这说明Ra数的增加对提高流体对流换热效果有着积极的作用。

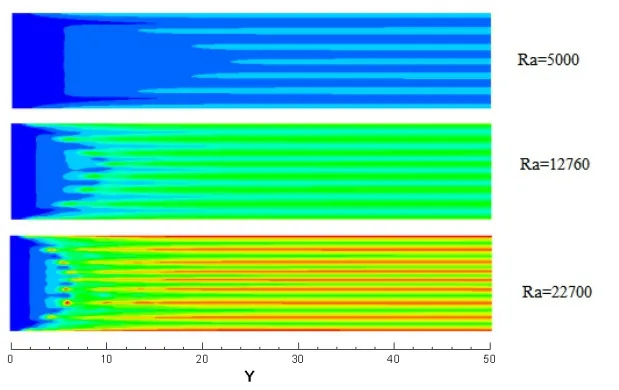
图4 Re=10时不同Ra数下Z=0.5截面的温度云图

3.结论

本文通过三维流体力学基本方程组的数值模拟，借助FLUENT软件研究了底部定温加热，上表面定温冷却的矩形通道内液膜的Poiseuille-Rayleigh-Bénard对流，分析了纵向流卷的演变过程和Re数和Ra数对流动的影响。主要结论如下：（1）在所取的参数范围内，由于封闭通道上下表面存在温差，通道中出现纵向流卷形式的二次流。纵向流卷由侧壁效应引起。流卷首先发生在侧壁附近，然后逐渐向中间移动。（2）Re数的增加对纵向流卷的个数没有影响，但会延长充分发展段出现的位置。（3）Ra数的增加会使纵向流卷的个数增加，使入口段长度减小。