基于Weibull模型聚丙烯纤维水泥砂浆冲击寿命分析

徐梓凌, 姜久红, 王云飞, 刘泽立

(湖北工业大学土木建筑与环境学院 湖北 武汉 430068)

众所周知,作为建筑领域不可或缺的一部分,混凝土被广泛的应用于工程领域。例如桥梁结构、桩基础、飞机跑道、堤坝及海洋作业平台。这些建筑在其服役过程中会受到各种动荷载的作用,如行车荷载、飞机着陆、海浪和地震等动态荷载作用,不可避免的人为因素和自然因素使得混凝土结构的安全性面临严峻挑战。因此研究混凝土结构在冲击荷载作用下的抗冲击性能对混凝土结构防灾减灾具有重要意义[1-3]。聚丙烯纤维是一种抗酸碱、强度高、模量高、抗冲击性和分散性良好的合成纤维。其作为增强纤维形成的建筑材料具有变形能力强、自愈合、多缝开裂以及优越的拉伸、断裂性能等优点已被材料学界和工程界所公认。刘晓鹏等[4]发现聚丙烯纤维可以显著提高混凝土的抗拉性能。郭琳等[5]在混凝土中掺入聚丙烯纤维并进行了一系列力学试验,试验结果表明适量的聚丙烯纤维可以很好的提升混凝土力学性能。宫巍[6]等发现聚丙烯纤维提升了混凝土的抗氯离子渗透的能力。Zhao J等[7]研究发现,随着聚丙烯纤维掺量的增加,混凝土抗冻融能力得到增强。靳哲鑫等[8]为提高混凝土的耐久性能,在混凝土中掺入聚丙烯纤维,试验结果表明聚丙烯纤维很好的改善了混凝土的抗渗性和抗硫酸盐侵蚀。

因为聚丙烯纤维可以很好的增加水泥基复合材料的力学性能和耐久性能,本文通过对聚丙烯纤维水泥砂浆进行抗冲击试验。基于对试验结果的分析,建立双参数Weibull分布概率模型,探究不同聚丙烯纤维掺量和不同直径下水泥砂浆的抗冲击性能[9-10]。结合双参数Weibull分布概率模型对水泥砂浆冲击寿命进行预测并冲击损伤演化规律进行研究。

1 试验概况

1.1 试验材料

水泥采用湖北省黄石市P.O 42.5华新普通硅酸盐水泥,其性能指标如表1所示。

表1 水泥性能指标

细骨料采用普通河砂,经过3 mm方孔筛过筛,细度模数为2.80。粉煤灰采用李坤电厂生产的Ⅰ级粉煤灰。改性聚丙烯纤维采用北京中纺纤建科技有限公司的干混砂浆专用纤维,性能指标如表2所示。纤维长度为8 mm,直径取20 μm、30 μm和48 μm 3种不同直径。减水剂采用聚羧酸高性能减水剂(粉剂)。水为试验用水。

表2 改性聚丙烯纤维指标

1.2 配合比

试验配合比见表3,水胶比为0.35。内掺0.3%、0.35%和0.4%体积率的聚丙烯纤维。试块尺寸为Φ150 mm×63 mm的圆柱体试块。表中PCM-0表示不掺纤维的普通组,PCM-1到PCM-3表示20 μm纤维直径下三种不同的体积掺量,PCM-a到PCM-c表示30 μm纤维直径下三种不同的体积掺量,PCM-m到PCM-k表示48 μm纤维直径下三种不同的体积掺量。

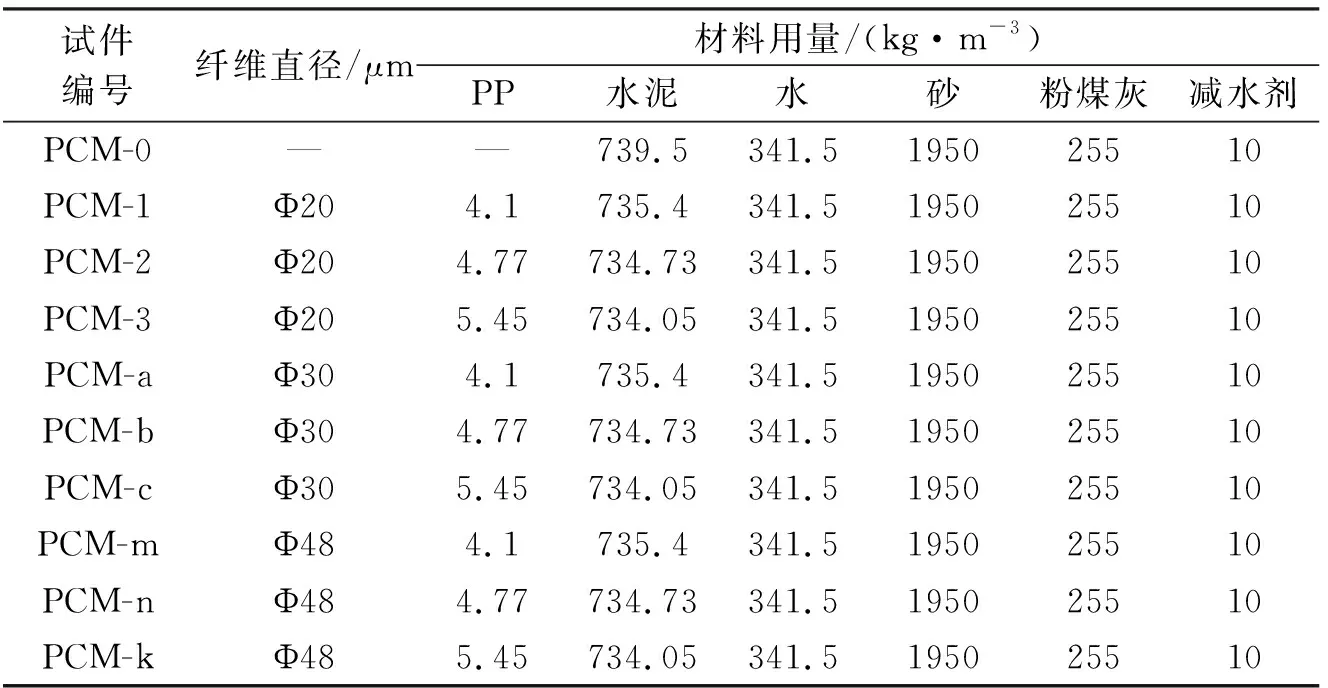
表3 试验配合比

1.3 试件制备与试验方法

采用水泥胶砂搅拌机进行试块的制备。考虑到聚丙烯纤维本身容易结团的属性,所以将纤维加入搅拌机之前,先对聚丙烯纤维进行分散处理。实验开始前首先润湿锅壁,用高精度的小称将各材料称量完毕。纤维砂浆在搅拌过程中经历慢搅120 s、停歇20 s、快搅120 s三个过程,为避免聚丙烯纤维在水泥砂浆中分布不均匀,对搅拌时间适当延长。搅拌结束后将拌合物浇筑于模具内进行充分振捣。振捣后置于阴凉处24 h脱模,将试块放入标准养护室内进行养护处理。

本试验采用CECS13-2009水泥砂浆落锤冲击试验机对试块进行抗冲击试验(图1)。

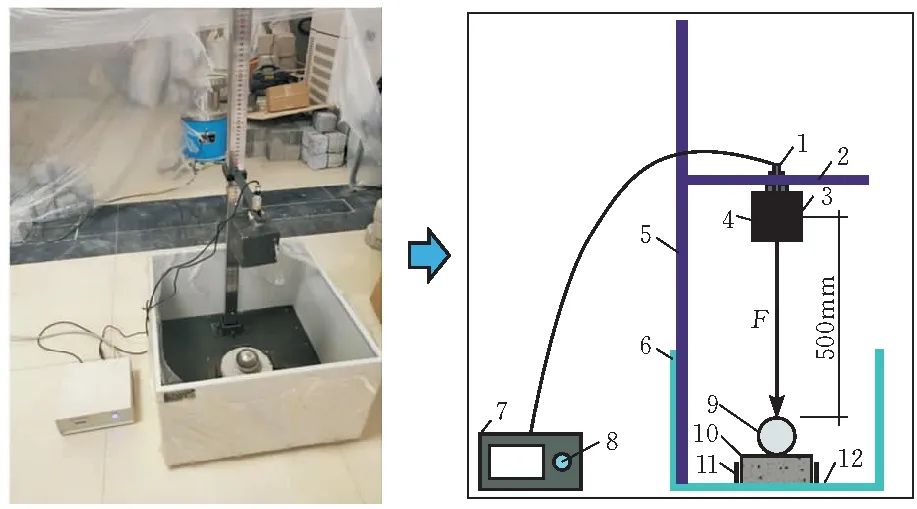
1-红外线装置;2-固定支杆;3-电磁装置;4-落锤;5-高度测量尺;6-挡板;7-控制装置;8-电磁开关和计数器;9-钢球;10-试块;11-挡板;12-底座支撑

冲击试验方法为,先将Φ150 mm×63 mm的圆柱体试块放置于底盘上四块挡板内,试块距挡板5 mm,上面放置Φ63 mm的钢球。打开电磁开关上的红外装置,将红外线照射至钢球球心点处。后将试验装置落锤高度固定在规范高度,落锤质心与试块上钢球表面的距离为500 mm。控制落锤的电磁开关上连接了计数器,通过电磁开关的按钮控制落锤进行冲击,每按一次按钮,计数器会记录一次冲击次数。随着冲击次数的增加,当试块出现第一条可见的裂缝时,视为初裂,记录下此时的冲击次数。当试块被冲击至开裂并能碰到周围三块挡板,视为终裂,记录下此时的冲击次数。

2 试验结果和数据分析

2.1 抗冲击性能

本试验通过水泥砂浆的冲击耗能W体现抗冲击性能的强弱,冲击耗能W的计算式如式(1)所示。初裂次数N1、终裂次数N2和冲击耗能试验结果如表4所示。

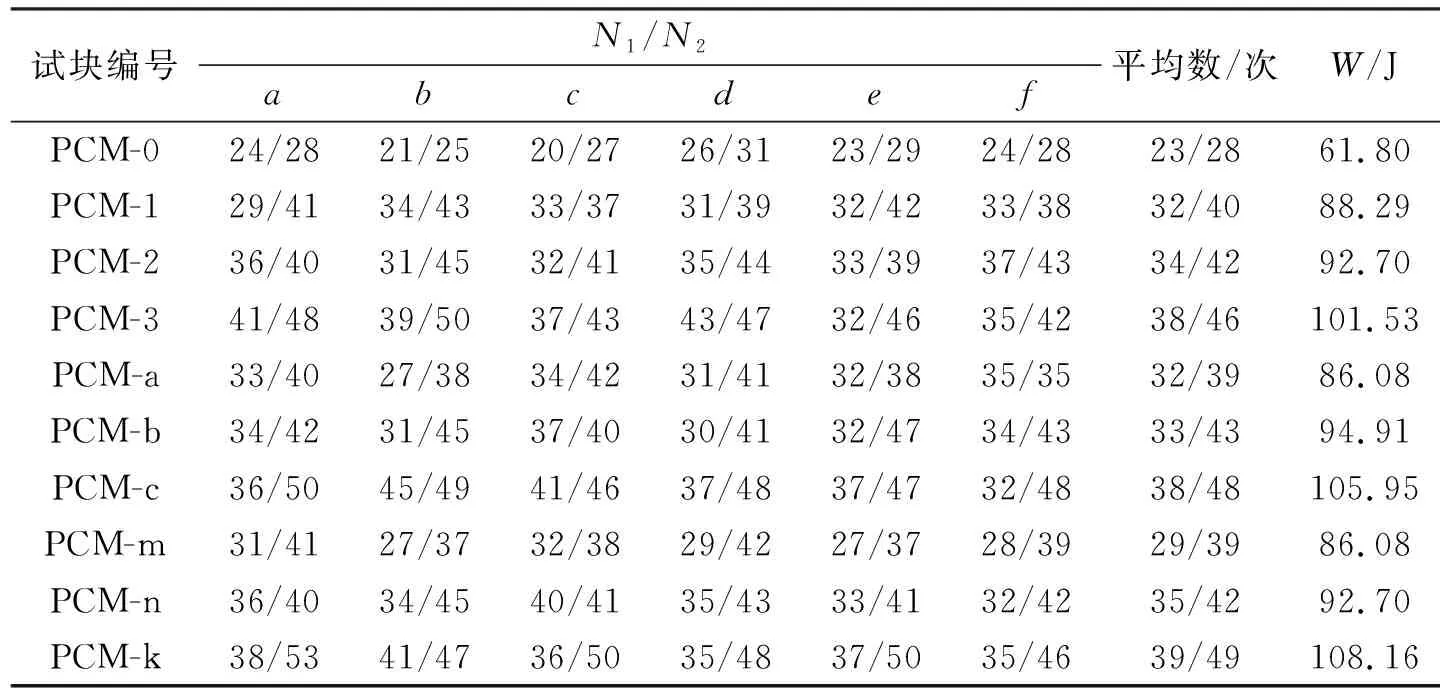
表4 聚丙烯水泥砂浆冲击试验结果

W=N2mgh

(1)

式中:W为冲击耗能,J;N2为终裂次数,次;m为冲击锤质量,kg,取4.5 kg;g为重力加速度,m/s2,取9.81 m/s2;h为落锤高度,m,取0.5 m。

由表4可以看到,由于水泥砂浆本身离散性较大,初裂次数N1和终裂次数N2离散性也较大,所以对每组6个试块的初裂次数N1和终裂次数N2取平均值,按照式(1)计算冲击耗能W。通过表2可以发现聚丙烯的掺入显著的提升了水泥砂浆冲击耗能W,这表明聚丙烯纤维的掺入很好的提升了水泥砂浆的抗冲击性能。

通过绘制冲击耗能W的等高线图(图2)。分析聚丙烯纤维掺量和直径及其交互作用对水泥砂浆抗冲击性能的显著程度。由图2可以看见冲击耗能等高线图中,随着聚丙烯纤维掺量增加,颜色变化由蓝逐渐转向红色,这表示水泥砂浆抗冲击性能随聚丙烯纤维掺量的增加普遍得到了提升。值得注意的是,纤维直径的变化对水泥砂浆抗冲击性能的影响并不明显。而等高线中横坐标的等高线的密集程度大于纵坐标的等高线密集程度,表明聚丙烯纤维掺量对水泥砂浆抗冲击性能的影响高于纤维直径。可以看到当聚丙烯纤维掺量为0.4%,纤维直径为48 μm时,水泥砂浆抗冲击性能最高,这表明水泥砂浆在该材料掺量下水泥砂浆抗冲击性能最佳。

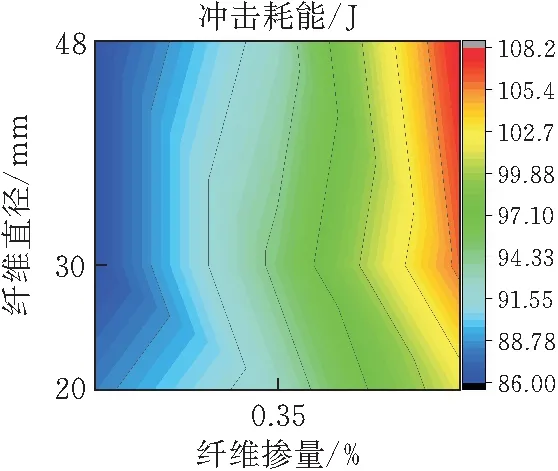
图2 冲击耗能等高线图

2.2 改性聚丙烯水泥砂浆内部结构分析

由图3可以看到。普通水泥砂浆主要是由胶凝材料和细骨料颗粒组成。随着聚丙烯纤维的掺入,水泥砂浆内部结构的组成发生了变化。水泥砂浆在受到外界荷载作用下,在内部的细小裂缝处会发生应力集中,这会导致裂缝不断延伸拓展。随着荷载的增大,这种应力集中效应越来越明显,从而造成水泥砂浆的破坏。但聚丙烯水泥砂浆中在受到外界荷载作用时,由于聚丙烯纤维的桥接作用,使得聚丙烯纤维与周围胶凝材料能够形成一个复合受力体系。在裂纹尖端会产生一个反方向的应力场,从而阻碍裂缝的产生。在水泥砂浆内部结构中,纤维与水泥浆体之间是通过材料界面粘结相互作用的,这种受力体系使得水泥砂浆强度得到了提升,韧性得到了加强。从而水泥砂浆的抗冲击性能也得到了增强。

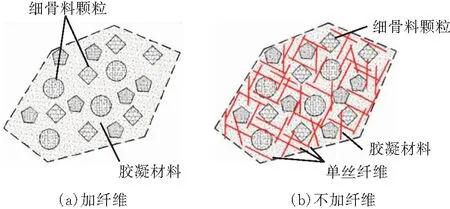
图3 水泥砂浆内部构造

2.3 基于Weibull分布概率模型的水泥砂浆抗冲击次数分析

由于水泥砂浆内部存在大量不成规律的微裂缝、微孔隙等缺陷,使得水泥砂浆在反复落锤冲击下产生的损伤具有很大的随机性。冲击损伤可被看作随机分布变量的一种,这种随机分布变量必然会符合某一类型的统计学规律。Weibull分布概率模型已作为寿命预测模型大量运用在脆性材料的失效评估上,因此选用Weibull分布概率模型探究水泥砂浆经过反复落锤冲击后的宏观损伤演变规律。

Weibull分布概率模型是由Waloddi Weibull在研究材料疲劳寿命问题时提出来的三参数函数,如:

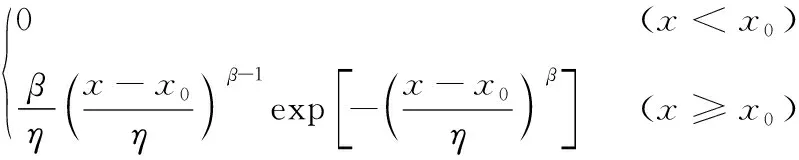
(2)

式中:β为韦伯形状因子;η为尺度因子;x0为位置参数,且x0≥0。

当位置参数x0=0,那么三参数Weibull分布函数就简化为二参数Weibull分布函数,如:

(3)

对式(3)进行积分,得到相应的概率密度分布函数为:

(4)

则水泥砂浆累计失效概率函数为:

(5)

由此可得水泥砂浆存活概率函数为:

(6)

此分布模型建立了冲击次数与水泥砂浆失效概率之间的关系,随着落锤冲击次数增加,水泥砂浆失效概率也会增加,达到某一特定的冲击次数N之后,P1(N)=1。对式(6)两边取两次自然对数,可得:

(7)

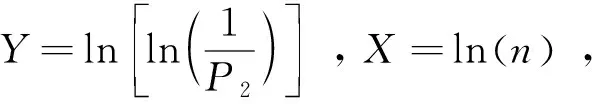
Y=a+bX

(8)

即X与Y之间存在近似的线性关系,通过线性回归分析,得出参数a、b以及相关系数R2的值。当R2的值较大时,表明Weibull分布概率模型可以对水泥砂浆抗冲击寿命进行合理的描述。在小样本条件下(冲击试验单组试块的样本总数为6块),将样本的观测值按照从小到大的次序排列,采用平均秩法的期望估计来计算水泥砂浆存活概率函数,则:

(9)

式中:m为每组试块的样本总数;i为其中某组试验数据按从小到大排列后的秩序数。

通过以上式子,如果可以观察到X和Y之间存在近似的线性关系,就能够证明双参数Weibull分布概率模型可以有效的对聚丙烯纤维水泥砂浆的冲击次数进行统计分析。将表3数据按照式(7)—式(9)进行计算。以X为横坐标,Y为纵坐标,进行线性回归分析(图4)。得出参数a、b和相关系数R2,结果见表5。

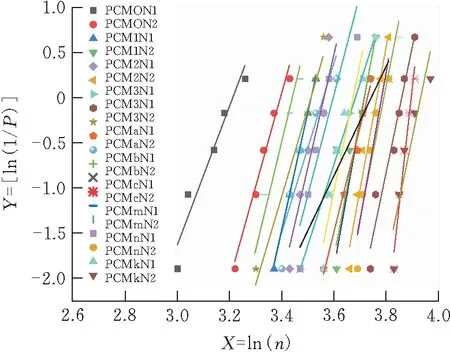
图4 Weibull线性回归曲线

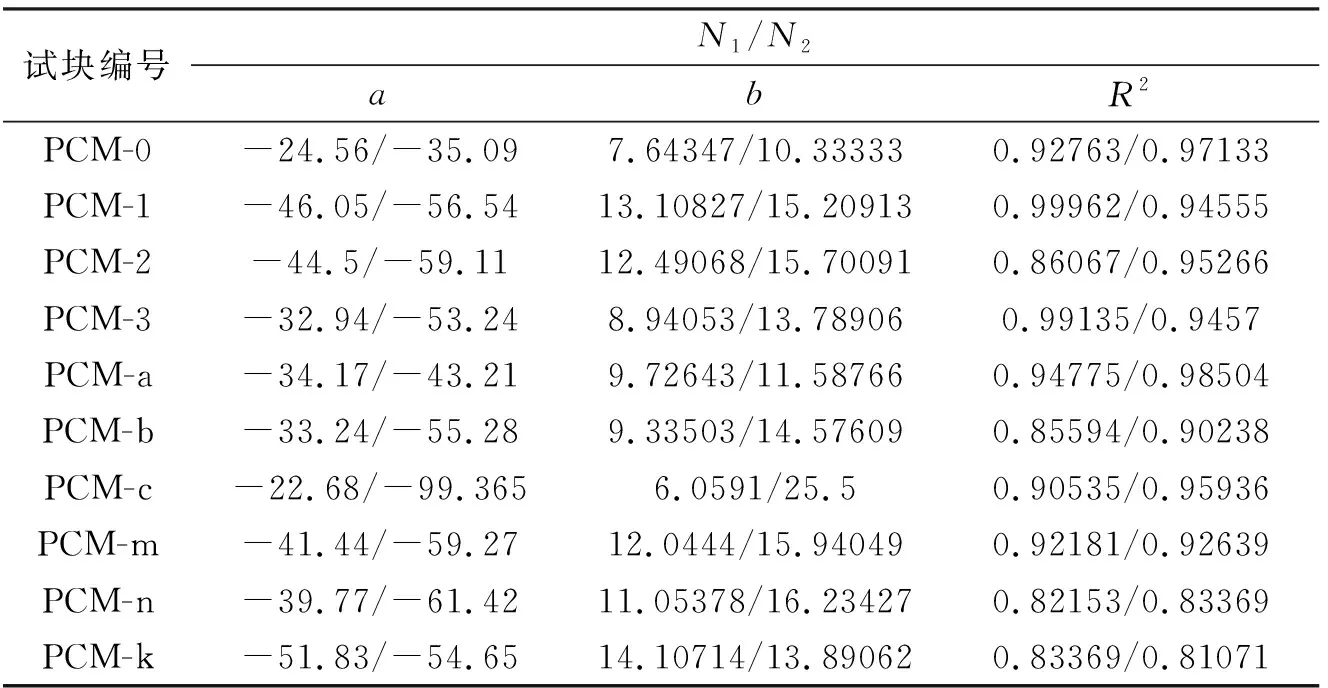
表5 聚丙烯水泥砂浆冲击次数Weibull线性回归结果

由表5可知,采用双参数Weibull线性归回分析。聚丙烯纤维水泥砂浆抗冲击次数的回归系数最大值为0.99962,且其余组别回归系数大部分高于0.9,有小部分低于0.9,但均高于0.8。这表示双参数Weibull分布概率模型适用于聚丙烯纤维水泥砂浆初裂冲击次数和终裂冲击次数的统计分析。

根据式(5)、(6)、(7)、(8)进行变形可得式(10),在不同的失效概率P1下对水泥砂浆冲击次数N进行分析估计。

(10)

式中参数a、b从表5获得。

通过式(10)可以求得不同失效概率P1下水泥砂浆初裂冲击次数N1和终裂冲击次数N2。取失效概率P1为30%、50%和70%,对水泥砂浆的冲击寿命进行分析和估计,各组别冲击寿命估计值见表6。不同失效概率下,水泥砂浆冲击寿命也不相同,但冲击寿命变化趋势均符合试验数据变化趋势。失效概率为0.5时,水泥砂浆的可靠率为0.5,此时水泥砂浆的冲击寿命更加符合实际工程情况。

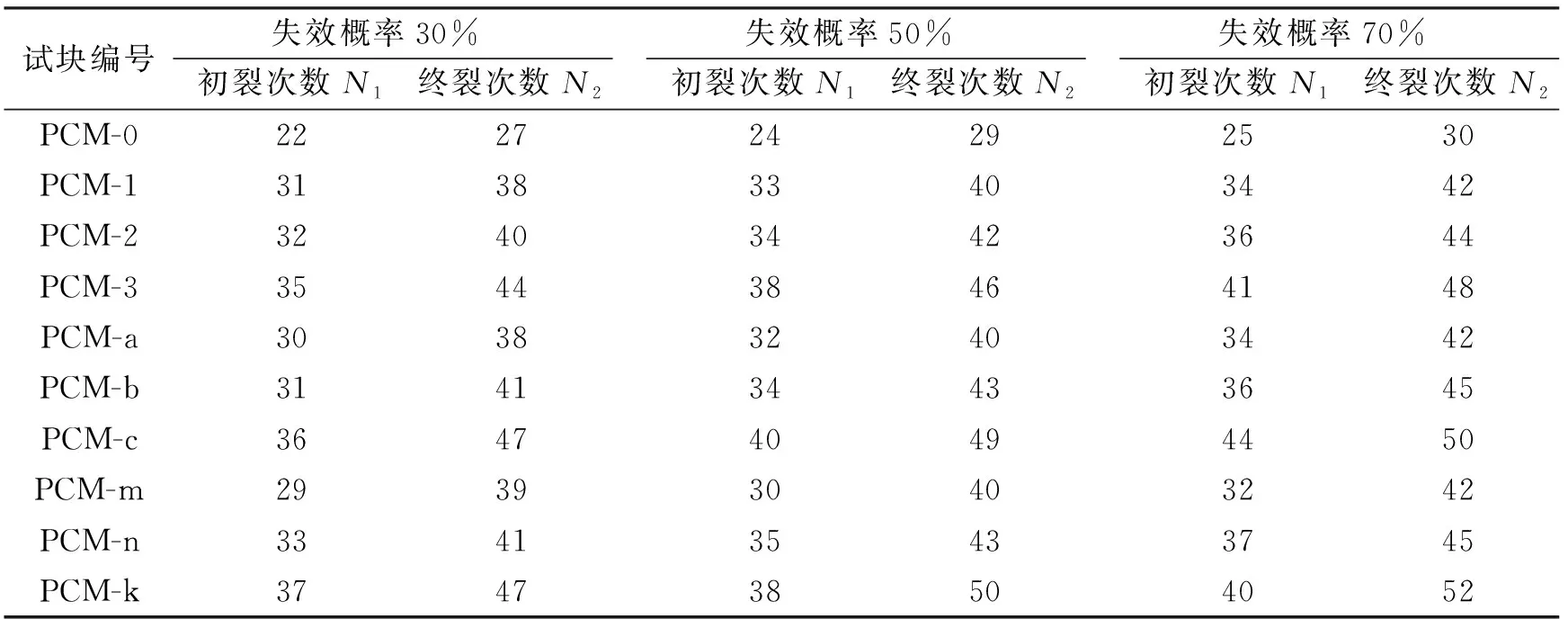
表6 不同失效概率下的聚丙烯水泥砂浆抗冲击次数

将失效概率为0.5时的初裂和终裂次数与实际试验数据之间进行对比(图5)。由图5可以看到,通过双参数Weibull分布概率模型统计分析导出的预测数据与试验数据的相对误差非常小,数值间的相对误差仅在0.6%～11.1%之间,初裂次数和终裂次数的平均相对误差为4.21%和3.52%。

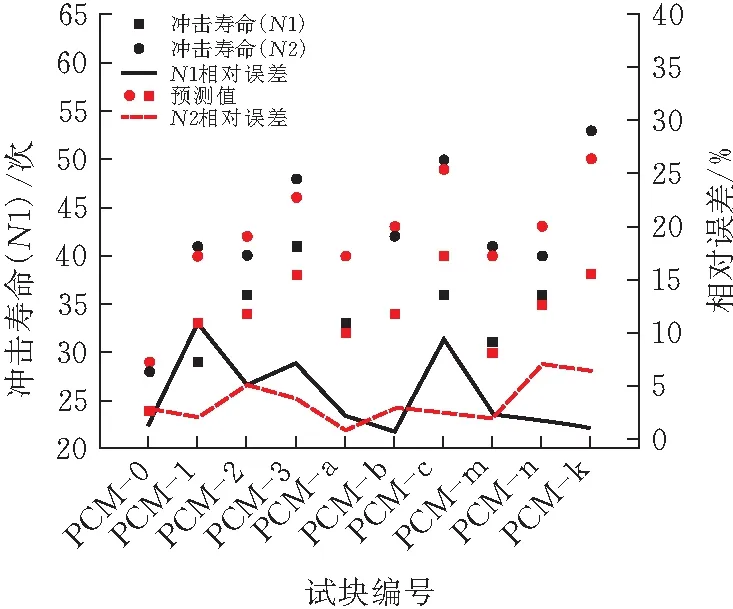
图5 预测数据与试验数据的相对误差

2.4 基于Weibull分布概率模型的水泥砂浆冲击损伤分析

利用双参数Weibull分布概率模型的统计分析对水泥砂浆冲击荷载下的初裂和终裂次数进行了预测,但没有系统研究水泥砂浆从遭受第一次冲击荷载直到发生破坏的损伤变化。所以在后续的研究中,通过双参数Weibull分布概率模型来探究水泥砂浆经过反复落锤冲击后的宏观损伤演变规律[11-12]。

水泥砂浆经过n1次落锤冲击后,水泥砂浆失效概率为P1(n1),产生的损伤度为D(n1);当水泥砂浆经过N次落锤冲击后发生失效破坏时,水泥砂浆失效概率P1(N)=1,损伤度D(N)=1,由此可见,可将水泥砂浆失效概率和损伤度进行等效处理,即有:P1(n)=D(n)。

综上所述,基于二参数Weibull概率分布的水泥砂浆冻融随机损伤模型可写为:

(11)

通过表5结合式(7)和式(8)可求得β和η,后将计算结果代入式(11)可得出各组水泥砂浆在冲击荷载作用下损伤演化方程(表7)。并画出各组冲击寿命的损伤演化图(图6)。

表7 水泥砂浆双参数Weibull分布损伤演化方程

各组水泥砂浆冲击破坏损伤演化如图6所示。由图6可以看到聚丙烯水泥砂浆在反复冲击荷载下寿命的损伤演化趋势。在聚丙烯水泥砂浆抗落锤冲击的前期阶段,水泥砂浆的损伤度变化幅度很小。但是随着落锤冲击次数不断的增加,聚丙烯水泥砂浆损伤度的增长幅度非常大。可以看到损伤度并不是以直线趋势发生变化,而是以曲线趋势发生变化,这也表明聚丙烯水泥砂浆在抗冲击破坏的前期阶段表现出了很好的延性。水泥砂浆的冲击寿命随着聚丙烯纤维掺量的增加而得到了增长。

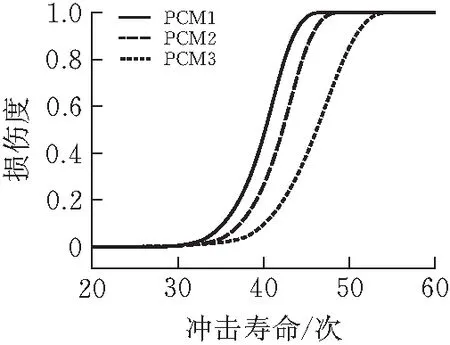
(a)缺图题

3 结论

1)聚丙烯纤维的掺入很好的提升了水泥砂浆的抗冲击性能。随着聚丙烯掺量的增加,水泥砂浆的抗冲击性性能不断的增长。但是随着聚丙烯纤维直径的增大,这种增长并不明显。聚丙烯纤维掺量对水泥砂浆抗冲击性能的影响要大于聚丙烯直径。当聚丙烯纤维掺量为0.4%,纤维直径为48 μm时,水泥砂浆的抗冲击性能最好。

2)通过聚丙烯纤维的桥联作用,在水泥砂浆中掺入适量聚丙烯纤维,使水泥砂浆内部构造中纤维与周围胶凝材料能够形成一个复合受力体系。这种变化使得水泥砂浆冲击性能得到了提升,韧性得到了加强。

3)采用双参数Weibull分布概率模型对冲击次数进行统计分析,通过数据拟合建立了冲击次数N和失效概率P之间的函数关系。结果表明双参数Weibull分布概率模型可以有效的对冲击次数进行统计分析,在失效概率P为50%时,初裂次数和终裂次数的预测值与实际值的平均误差仅为4.21%和3.52%。通过双参数Weibull分布概率模型得出聚丙烯水泥砂浆在反复冲击荷载下寿命的损伤演化趋势,为实际工程中的推广和应用提供了参考。