基于交直流最优功率分配的动态分层LFC方法

龚偲立, 赵熙临

(湖北工业大学电气与电子工程学院, 湖北 武汉 430068)

负荷频率控制(load frequency control,LFC)是维持电力系统稳定运行的关键技术,能够根据负载变化实时调整发电机组出力,保证电力系统频率偏差尽快回到允许范围内[1-2]。随着可再生能源的大规模并网和高压直流输电线路的广泛应用,尽管电网强交弱直的特征得到改善,但频率波动的风险性逐渐增大,对传统LFC方法提出了新的挑战[3-4]。因此,如何在可再生能源占比较高前提下,应对弱连接的交流联络线潮流波动较大的问题,是现阶段电力系统调频工作的研究重点。

新能源渗透率的大幅度提高与跨区域输电需求的增加,使高压直流输电(high-voltage direct current,HVDC)线路的建设规模扩大,交直流混联系统在复杂电网运行中的应用愈加广泛[5-6]。现阶段,国内外学者针对交直流混联系统的协调运行做了相应的研究。文献[7]分别对直流和交流电网内的分布式电源进行模糊自适应下垂控制设计,以消除线路阻抗的影响,保证有功功率和无功功率的合理分配。文献[8]基于风电不确定性和交直流输送容量载荷程度的不同,设计了一种交直流输电容量优化分配方法,可减小风电波动对交直流电网的影响。文献[9]采用快速非支配多目标遗传算法确定交直流混联系统的最优运行策略,增加电网电容量使得传统负荷频率控制特性发生改变。在强负荷扰动下,所需调频功率需交直流链路共同承担,而其分配方式不仅导致调频策略的复杂化,还会对电网经济运行带来影响。

当由于交直流功率分配及可再生能源不确定性等问题而导致电网负荷频率控制复杂度增加时,分层控制策略受到了广泛的关注[10-11]。文献[12]提出了一种基于两级分层模型预测的LFC策略,通过上层对下层分散控制器的动态协调来应对调频控制的复杂性。文献[13]设计了一种基于动态有功调度的分层模型预测控制策略,该策略以短期风电预测误差的分层分析作为反馈来提高风力发电的兼容性。但上述研究中分层控制结构两级均采用模型预测控制器(model predictive control,MPC),其滚动优化算法在线计算复杂度高,计算量大。针对该问题,文献[14]设计了一种基于MPC-PID串级的动态分层控制策略,根据调频需求的不同以区域控制偏差(area control error,ACE)作为触发信号,实时决策上层MPC是否参与。

另一方面,利用电网中可再生能源的固有特性或已存在的能源配置进行辅助调频,能够有效提高调频效果、减轻系统复杂性的不利影响。文献[15-16]利用储能电池充放电特性参与电网调频,并指出其调频能力相对于忽略爬坡速率约束的火电机组更具高效性。文献[17]结合了储能电池荷电状态(SOC)和电网调频的需求,给出了储能电池参与调频的评价指标,验证结果表明储能参与可改善电网的抗干扰能力。文献[18]分析了电池储能辅助电网一次调频的方法,提出的储能自适应综合控制策略能有效节省传统机组的调频容量。考虑到电力系统中储能配置的普遍性,基于对电网全局调控的需求,有必要在电力系统运行中充分挖掘储能辅助调频潜力,以应对日趋复杂的LFC应用需求。

综合而言,进一步的研究需要解决以下两个方面的问题:一是针对交直流链路传输特性,如何根据链路传输容量进行传输功率的分配,以提高电网运行的经济性与安全性;二是在复杂调频需求的动态变化前提下,如何使调频策略体现出动态的适应性。

1 含储能的交直流混联电网LFC模型构建

以多区域LFC系统为研究对象,当考虑储能的辅助参与时,区域交直流混联LFC系统控制模型如图1所示,相关变量的含义如表1,各单元模型可参考文献[19]。

表1 LFC系统参数

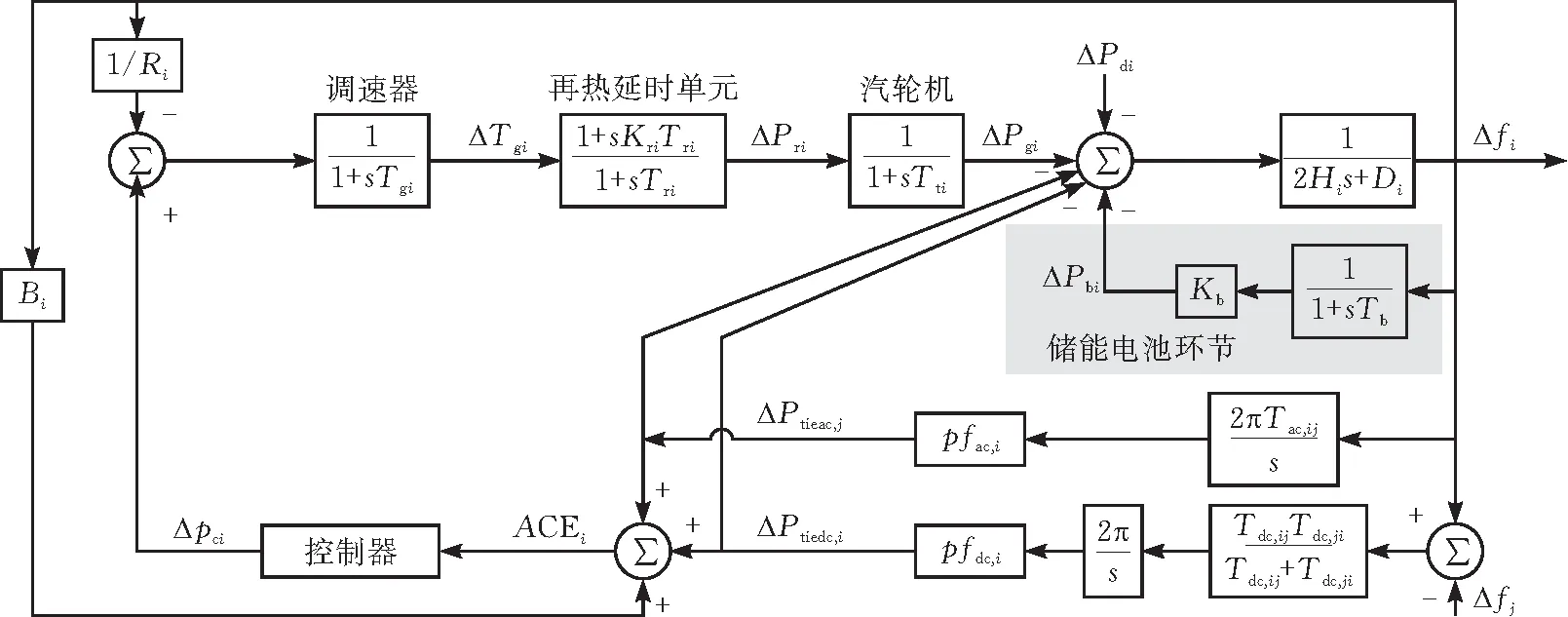
图1 含储能的交直流混联区域LFC模型

以多区域LFC系统为研究对象,为了提高调频效果,减轻系统复杂性的不利影响,设置储能进行辅助调频。区域交直流混联LFC系统控制模型如图1所示,相关变量的含义如表1,各单元模型可参考文献[15]。

当储能以虚拟惯性和下垂控制辅助LFC系统参与一次调频时,其综合惯性控制响应模型一般等效为一个惯性环节[16],表示为:

(1)

式中:Kb为储能电池的单位调节功率,Tb为储能电池的时间常数。

根据图1的汽轮机热力学模型和联络线一阶传递函数可以得到区域i的频率偏差:

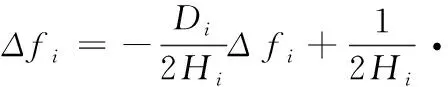
(2)

式中:联络线功率偏差ΔPtie,i为直流联络线功率偏差ΔPtiedc,i和交流联络线功率偏差ΔPtieac,i之和,其余各变量描述参见表1。

而其ACE信号由本区域的频率偏差和联络线功率构成,具体表示为:

ACEi=BiΔfi+ΔPtie,i

(3)

以区域频率偏差,交直流联络线功率偏差,储能电池、汽轮机、调速机和控制器的输出构成的向量为系统状态变量,控制器输出向量为输入变量,区域i的区域控制偏差为输出变量,可获取区域i状态方程为:

(4)

式中:x、u、w分别表示该系统的状态变量,输入变量和扰动变量;A、B、C、D分别表示该系统的状态矩阵、输入矩阵、输出矩阵和扰动矩阵。各状态变量和状态矩阵的具体表达式如下:

x=[ΔfiΔPtiedc,iΔPtieac,iΔPgiΔXgiΔPri]T

(5)

u=ΔPci

(6)

ω=ΔPdiT

(7)

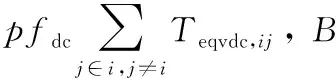
上述模型中pfac,i和pfdc,i分别表示交直流联络线承载的有功功率分配因子,直流联络线等效增益Teqvdc,ij=Tdc,ijTdc,ji/Tdc,ijTdc,ji。

2 基于最小网损的交直流最优功率分配

交直流联络线承载有功功率分配的差异性将导致调频表现及电网运行经济性上的不同,在此,拟以网损最小为目标进行交直流最优功率分配策略(optimal power allocation control,OPAC)的研究。

图2描述了多电源交直流混联电网结构,考虑到每个交流节点和直流端口注入的有功功率以及直流端口电压,其总网损的计算公式由交流网损Ploss,ac和直流网损Ploss,dc两部分组成[17],即:

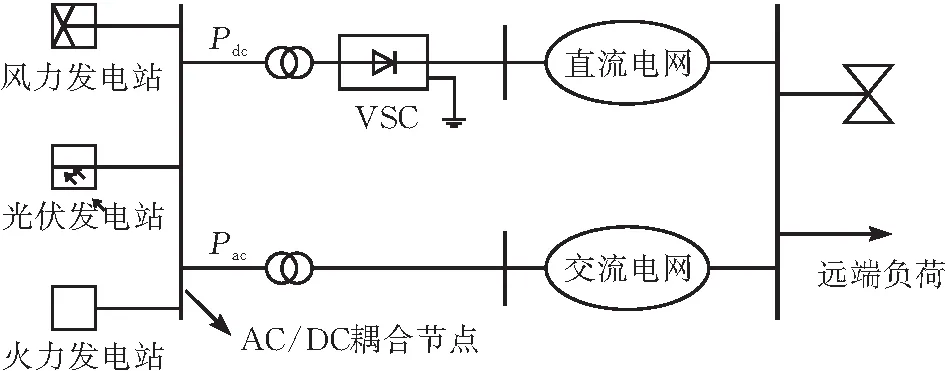
图2 交直流混联电网示意图

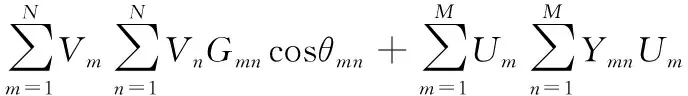
(8)

式中:N,M分别为交流电网的节点数和直流电网中的端口数,V为节点电压幅值,Gmn为节点导纳矩阵的实部元素,θmn为节点m和n之间的向角差,Um为端口电压,Ymn为端口电导矩阵中的元素。

交流链路中,长距离输电线路电阻较小,其网损与节点电压幅值主要由无功功率决定,节点相角由有功功率决定,其中Gmn属于已知参数。利用潮流计算模型,可将节点m和n之间的相角θmn用Pac线性表示为:

(9)

式中:xk是节点导纳矩阵的逆矩阵元素

取cosθmn泰勒展开公式的一次项和二次项,联立(9)可得cosθmn为:

(10)

将式(10)代入式(8),可得到交流网损是关于AC/DC耦合节点注入的有功功率多元二次函数:

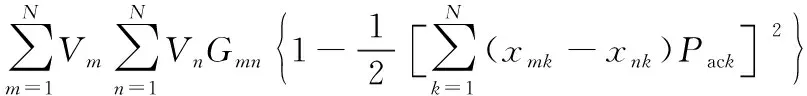
(11)

通常情况下,直流电网的各个换流站的端口电压Um与参考电压Uref较为接近,则可得到在PV控制模式下各个端口注入的有功功率端口电压之间的数学表达式为:

(12)

假设第M个换流站用于控制直流电压,将Um=Uref代入(12),各换流站注入的有功功率和端口电压之间的线性关系可表示为:

(13)

式中:Rmk为端口导纳矩阵的逆矩阵元素;其中m=1,2,…,M-1。

将式(13)代入到式(8)可得到直流电网的网损表达式Ploss,dc。除了注入到AC/DC耦合节点的换流站,其余换流站注入的有功功率均为已知量。由于注入到AC/DC耦合节点的交流线路和直流线路的功率均可以调整,将交流联络线中的有功功率作为自变量,再根据Pacm+Pdcn=Ptie消除直流联络线的有功功率后,则式(8)可表示为一个二次函数:

(14)

式中:Pac=[Pac1,Pac2,…,Pacr],r是AC/DC耦合节点的个数,Pac1,Pac2,…,Pacr为对应节点的交流有功功率。Q和C分别是由多元二次函数Ploss,ac和Ploss,dc推导出来的系数矩阵和常数项。

如图2所示当仅有一个AC/DC耦合节点,同时作为交流电网的第t个节点和直流电网中的第s个换流站,则式(14)改写为:

(15)

式中:

针对交流有功功率Pact构造网损最小的优化目标:

(16)

交流联络线输送容量的不等式约束为gmin≤g(x)≤gmax,将其转化为w个等式约束后,式(15)满足如下约束条件:

J2(Pact)=ci,i=1,2,…,w

(17)

利用拉格朗日乘子法将该多元函数进行转换,并令各状态变量的一阶偏导数为0,可得由w个方程组成的方程组:

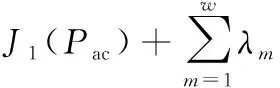
(18)

式中:▽J(*)表示为函数J的梯度。

求解(15)可以得到网损最小值时各个AC/DC耦合节点对应的交流联络线有功功率。根据交流联络线与联络线总功率之间的关系,可调整LFC模型中的直流线路和交流线路的功率配比因子pfac,i,pfdc,i。

上述模型中pfac,i和pfdc,i分别表示交直流联络线承载的有功功率分配因子,直流联络线等效增益Teqvdc,ij=Tdc,ijTdc,ji/Tdc,ij+Tdc,ji。

3 基于最优功率分配的动态分层LFC控制方法设计

3.1 动态分层控制策略设计目标与影响因素分析

在众多控制方法中,单一的比例积分微分控制(proportional predictive control,PID)不能满足复杂的LFC控制需求。为了实现控制目标,模型预测控制得到广泛使用。但是,由于MPC采用滚动优化算法,扩大了在线计算的复杂度,严重占用了系统资源。因此,为了将系统控制过程的复杂度与调频需求的多样性进行匹配,有必要构建具备选择特性的动态分层控制架构。如图3所示,下层采用PID控制器,能保证弱调频需求下调频过程的快速性,从而有效节约系统资源。对于强调频需求,采用上层MPC控制器和下层PID控制器级联的方式可实现调频的精准性。上层控制器是否参与由各区域电网两层控制器之间的虚拟选择开关Si决定。触发信号为区域系统控制偏差信号Ai,该信号由电网调度控制系统(grid dispatching and control system,GDACS)采集,并将其传递给条件驱动环节(conditional drive link,CDL)用于判断Si的动作情况。

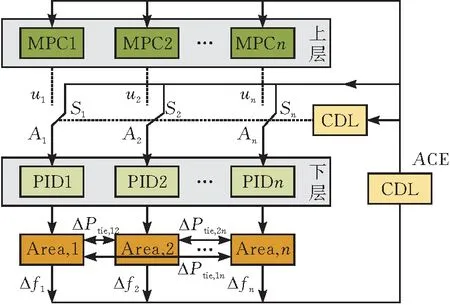
图3 动态分层LFC控制系统

在控制过程中,区域控制偏差是平衡LFC系统有功功率的重要度量指标,将其作为条件驱动环节的触发信号有利于精准控制的实施。由于ACE信号计算涉及区域频率偏差Δf和区域对外联络线交换偏差ΔPtie,ij,因此在设计ACE信号的驱动阈值时,需要根据各区域电网的实际规模、联络线功率约束条件和频率调节死区等对其进行处理。

当各区域电网的ACE信号Ai达到相应的驱动阈值Aref,i时,CDL触发上下控制器之间传输线的虚拟开关Si闭合,使上下层控制器串联,有利于提高控制效果。当Ai小于相应的驱动阈值Aref,i时,该区域的虚拟开关Si断开,仅下层PID控制器参与调频,保证了区域控制的快速性。在Aref,i的设计中,如果调频需求聚焦于控制的精确性,可设计较低的阈值;如果目标聚焦于降低在线计算复杂度,可设置较高。

3.2 基于最优功率分配的动态分层控制策略设计

考虑交直流最优功率分配时,由于负荷波动的随机性,会存在以下两种情况。当负荷波动较小,LFC各发电机组出力变化不大时,输送的功率波动全部由交流联络线承担,直流联络线保持恒功率运行[18]。当负荷波动较大,LFC发电机组会相应的增加出力,此时按照最优功率分配策略,对交直流线路传输的功率进行优化,实现系统运行的经济性和安全性。

OPAC策略参与下,联络线有功功率变化情况如图4所示。t0时刻,联络线传输功率增加Pintie,需要调用直流联络线来承担一部分有功功率。t1时刻,投入OPAC策略,产生Ploss的功率损耗后对交直流线路的功率分配进行重新规划。最终出力突增后联络线有功功率按照最优功率分配因子pfac、pfdc由交直流联络线Pac,Pdc共同承担。

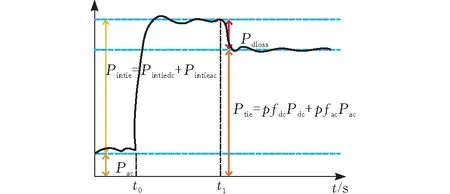
图4 交直流联络线有功功率变化示意图

基于超短期负荷预测和储能电池功率预测信息,由每时段的功率平衡方程可以推导出区域电网联络线功率波动量:

ΔPtie,i=ΔPL,i-ΔPb,i-ΔPG,i

(19)

在强负荷扰动下,区域LFC发电机组出力增加,联络线的输送容量也会相应增加。

结合第二节,利用交直流最优功率分配策略对直流线路和交流线路的功率配比因子pfac,i,pfdc,i进行计算调整,得出联络线功率表达式:

(20)

将式(20)代入式(3),并考虑在交直流最优功率分配策略的应用过程中直流电网和交流电网的功率损耗,此时,区域电网的ACE改写为:

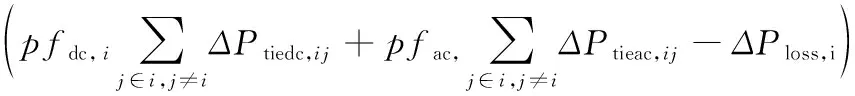
(21)

式中:ΔPloss,i为区域i基于交直流最优功率分配策略的总网损。

启动OPAC时区域控制偏差为AOPAi,则基于最优功率分配的动态分层控制策略具体流程见图5。

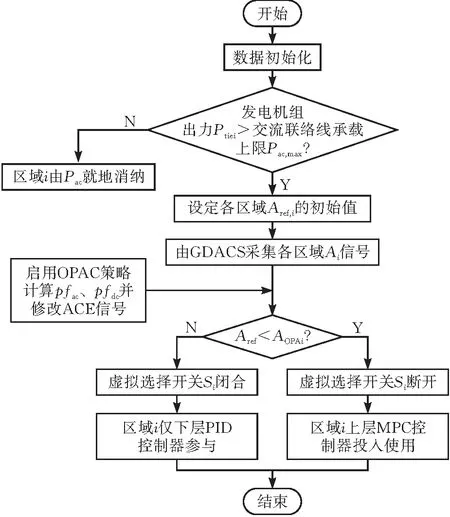
图5 基于OPAC的动态分层控制系统流程

4 仿真分析

不失一般性,以如图6含储能的三区域交直流混联电网为例进行分析,各区域交直流耦合节点均为一个。三个区域的火电机组容量分别是2200 MW、2400 MW和2600 MW。参考理想储能资源与传统发电机组的调频能力关系[20],设置各区域储能电池参数为17 MW。假设各原动机组均为满发,以基准频率50 Hz和机组额定容量为基准值对参数进行标幺化。取储能电池的单位调节功率Kb=20,以综合惯性控制方法辅助参与一次调频。在仿真过程中,参数设置为:采样周期Ts=0.03s,预测域Np=10,控制域Nc=3。其他相关参数设置情况如表2所示。

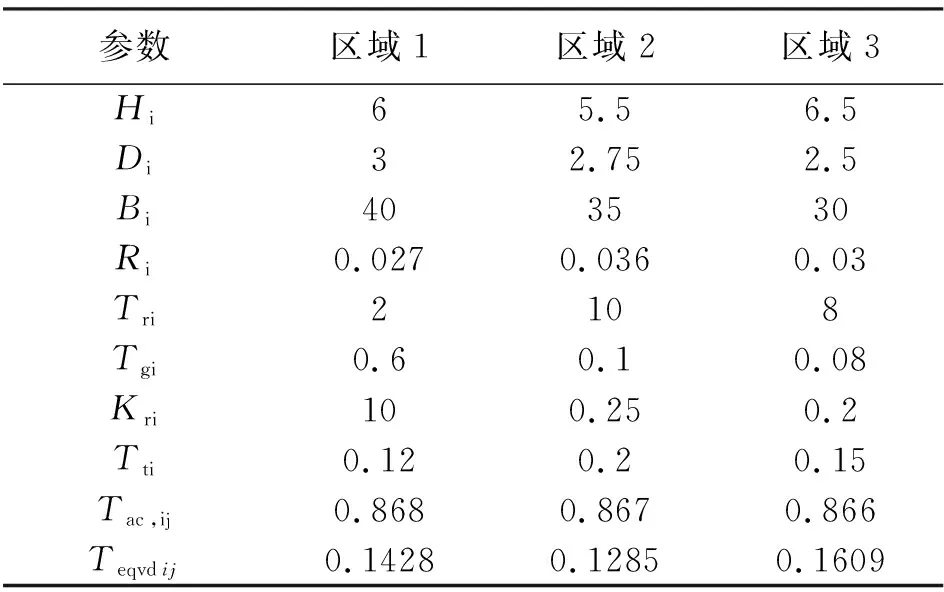
表2 LFC系统参数取值

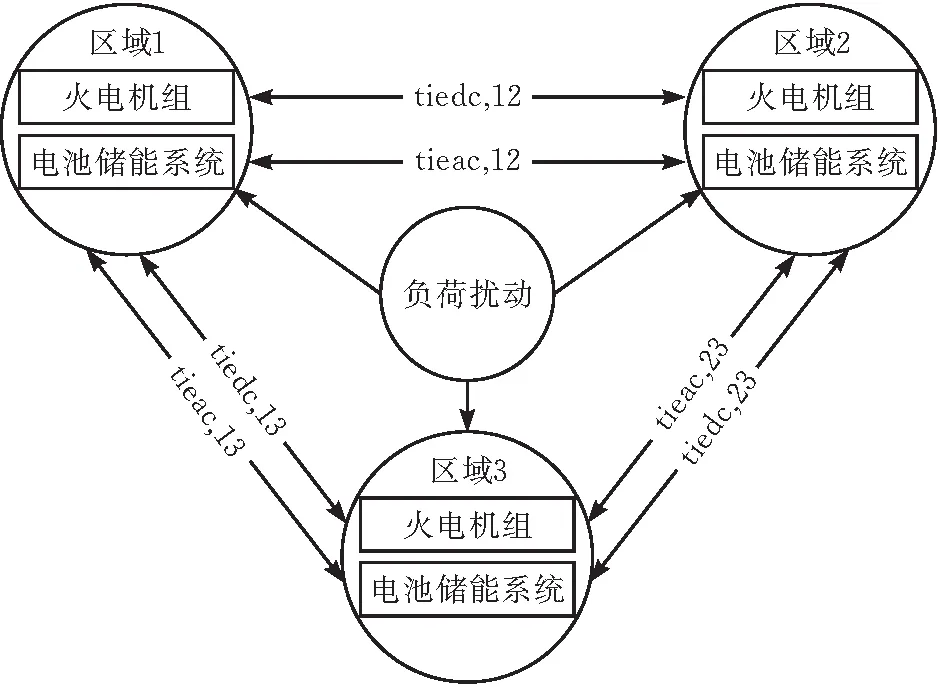
图6 三区域交直流混联电网模型

4.1 阶跃负荷扰动效果分析

考虑储能辅助调频时,交直流最优功率分配策略(OPAC)对LFC的影响,设定区域1的负荷扰动为0.1 p.u.,而区域2,区域3均不发生负荷扰动。设定区域1的驱动参考值为0.063 p.u.,对比分析DHC、POPID、OPAC-DHC和OPAC-POPID控制方法的响应性能,仿真结果见图7-9。

(a)交流联络线

当聚焦于联络线功率的变化时,对于同一控制策略,OPAC能使直流联络线分担一定的功率传输计划,从而降低交流联络线上有功功率的传输。由图7可知,在POPID控制方式下,交流联络线传输功率为0.012 p.u.;而在OPAC-POPID控制方式下交流联络线的有功功率约为0.005 p.u.,由此可见,OPAC降低40%左右的交流联络线传输计划。

对于动态分层控制策略的触发情况,由图8、9的仿真结果可知OPAC未参与时,区域控制偏差ACE1约为0.065 p.u.,达到了触发阈值, DHC策略中上下层控制器之间的触发开关S1闭合,此时为两级分层控制结构,DHC的频率偏差曲线和ACE曲线与POPID相吻合。而采用OPAC策略时,考虑到交直流电网网损,ACE1降低至0.061 p.u.,使其未达到触发阈值,此时仅下层PID控制器进行LFC的控制,达到节约系统资源的目的。各状态下调频效果及交直流功率分配具体数值对比如表3所示。

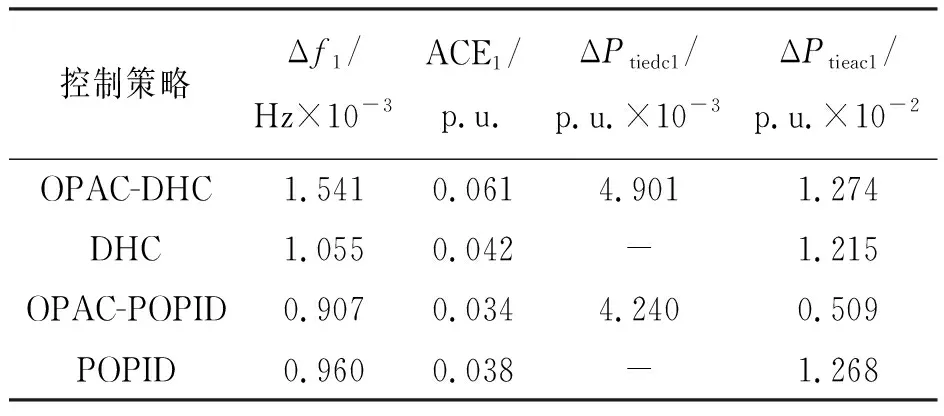
表3 阶跃负荷扰动下4类控制方法的控制性能对比

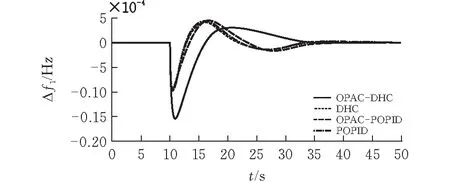
图8 阶跃负荷扰动下区域1频率偏差

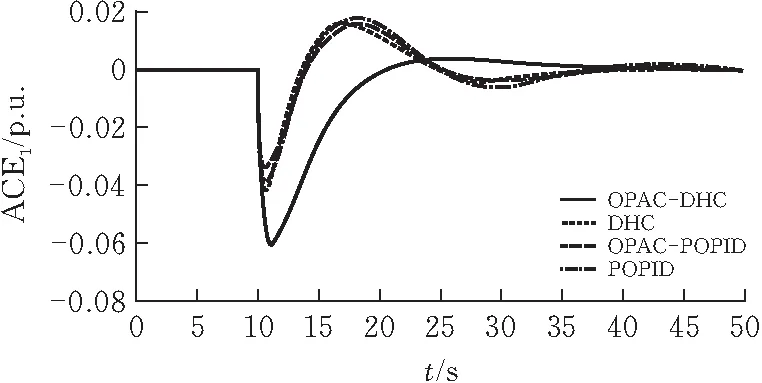
图9 阶跃负荷扰动下区域1区域控制偏差

4.2 随机负荷扰动效果分析

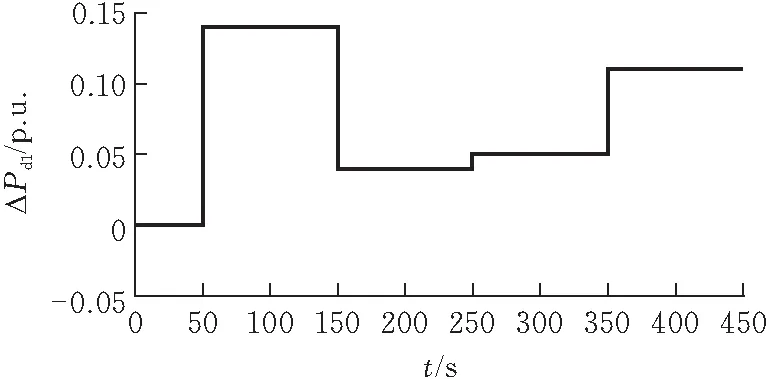
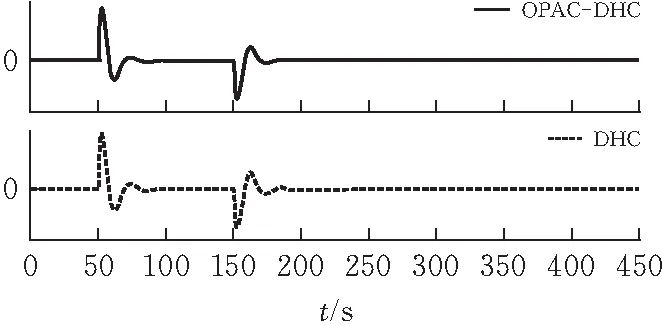
在三区域同时施加图10所示随机变化的负荷扰动,三个区域的驱动阈值分别设置为Aref1=0.07、Aref2=0.07、Aref3=0.05。此时,动态分层控制器上下层之间的虚拟触发开关Si运行情况如图11所示。以区域2为例,DHC的S2在150 s和350 s闭合,而采用OPAC策略后,与4.1的分析一致,降低了触发信号ACE的大小,使虚拟开关在这两个时刻未触发。

(a)区域1

(a)区域1

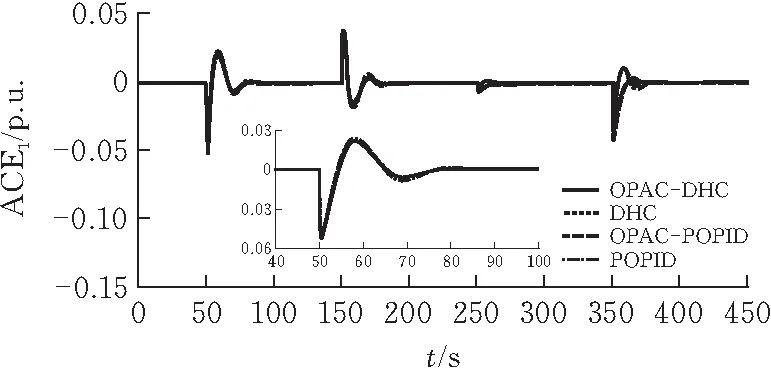
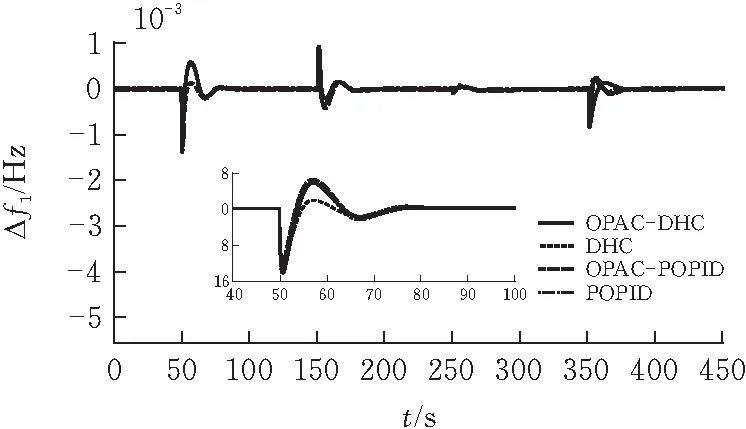
对应LFC控制器为OPAC-DHC、DHC、OPAC-POPID和POPID[19]时的系统频率偏差曲线和ACE响应曲线见图12-13。

(a)区域1

(a)区域1

对比三个区域不同控制方式的频率偏差曲线。在负荷扰动的作用下,区域1中较大的负荷扰动将导致较大的ACE1,若超过设定的阈值ACEref1=0.07 p.u.,则两级控制器间的虚拟开关S1被触发,动态分层控制系统的动态响应性能与预测优化控制方式的响应性能基本一致。若对应负荷扰动较小,区域1250 s时的区域控制偏差仅为0.010 p.u.,未达到阈值,则动态分层控制策略的上层控制器不被触发,尽管其控制性能会略差于相应的预测优化控制,但控制效果差距不大,而仅下层的PID控制器单独作用却可有效节约系统资源。

图14、15表现了各控制方式下各区域交直流联络线的功率的变化情况。对于POPID控制方式,进行OPAC功率优化分配之后,所有扰动下各区域交流联络线承载容量均减少45%左右,此时各区域的直流联络线分担了一部分减少的交流联络线传输计划。由于OPAC的功率分配优化可有效减少电网功率损耗,考虑随机负荷的情况也能够体现出与4.1阶跃响应类似的结果。

(a)区域1

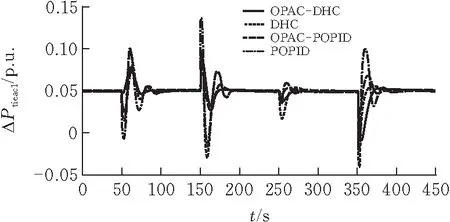
(a)区域1

5 结论

结合本文提出的基于交直流联络线功率优化分配的动态分层LFC控制策略,通过理论分析和仿真验证,可得出以下结论:

1)采用动态分层控制策略,能通过区域控制偏差的判断降低上层MPC控制器的触发频率,在保证电力系统频率控制性能无明显劣化的前提下有效节约控制系统资源。

2)当采用OPAC策略对交直流联络线进行功率优化分配时,不仅能最小化系统网损,还能有效降低区域控制偏差,保障动态分层控制等策略下控制复杂度的降低。