基于线性回归法的空间钢结构应力缺失数据重构

游 颖, 王 建, 刘游谦, 周清富, 彭 宁

(1 湖北工业大学机械工程学院, 湖北 武汉 430068; 2 湖北工业大学工程技术学院, 湖北 武汉 430068)

大跨度钢构件相互交错、造型复杂,对其进行应力应变的健康监测不可或缺[1]。由于在空间钢结构的长期监测过程中,可能会出现传感器精度问题引起数据不准确,设备意外损坏与故障以及监测数据传输的丢失等因素的影响,造成监测数据部分缺失,影响钢结构健康监测状态评估的准确性[2-4]。如何做好钢结构的应力监测,是一项巨大的技术难题[5-6]。监测数据不仅可以为此类结构安全性提供理论依据,还可为以后的相关建筑提供数据参考[4]。因此,钢结构应力缺失数据的修复对钢结构可靠性及完整度有十分重要意义[7-9]。

监测领域的数据重构方法主要有独立元分析法、主元分析法及其改进方法[10-13]。主元分析法是根据正常情况下监测系统的数据进行建模,将监测空间划分成主成子空间和残差子空间。当监测系统发生故障造成监测数据缺失时,未缺失的数据被映射到主成与残差子空间中进行多重迭代计算,通过逐渐拟合重构缺失数据。基于主元分析法对缺失数据进行重构时,需要监测数据服从正态分布,然而在实际监测过程中,实测数据往往不满足这个要求[10]。针对这种情况,研究者从独立元角度对正常状态下监测数据进行建模,基于相关的统计量原则对缺失数据进行重构[11]。钟蕾[12]基于独立元法对缺失的监测数据进行重构,对工业过程、优化及监控进行更好评估。刘飞[13]针对工业生产过程中数据缺失不能线性重构的问题,提出一种多尺度主元分析的监测数据故障重构模型,对火箭试车平台的供氢系统中误差数据、缺失数据进行数据重构,重构数据接近真实值。

目前对空间钢结构结构健康监测领域的研究多针对振动和位移监测数据的重构,而对监测数据链缺失的处理方法尚无相关研究,本文以国家网络安全人才与创新基地展示中心(简称“网安中心”)钢结构为研究对象,通过监测白天与夜晚钢构件在同一时间内的温度与应力数据,研究钢结构温度与应力的相关性,采用改进的线性回归模型,重构缺失的应力数据。

1 数据缺失来源和分类

1.1 数据缺失来源

在应力健康监测过程中,对监测设备的耐久性,监测系统的可靠性要求较高[14]。结构健康监测系统测点数量多、分布广,而且在无线监测中仪器的供能也是难题,同时大跨度钢结构施工现场的环境较为复杂,受外界因素影响较多,这些不可抗因素造成监测数据发生缺失的问题较为普遍。根据以往工程经验:缺失数据主要来源于以下四个方面:1)供能失效;2)传感器故障;3)数据传输失败;4)监测仪器意外损坏。

1.2 数据缺失分类

缺失类型:在空间钢结构长期健康监测中,数据缺失是采集仪器、传输设备,外界环境等诸多不可控因素造成,比如数据采集失败,数据传输失败等故障。这种监测点数据采集器和传输设备短时故障,会造成该监测点单个数据获取失败,监测数据链出现间断情况,这种类型的缺失数据称为离散型缺失数据。由于设备的老化在一段时间内连续发生故障或者损坏并且没有及时维修,将造成监测数据中一连串的数据缺失,将这种缺失类型的数据称为连续型缺失数据[15-17]。从以往的健康监测领域的经验中发现。这两类缺失类型是空间钢结构健康监测中最常见的缺失类型。

1.3 数据缺失修复

数据缺失处理的主要方法可以分为三类:删除法,插补法和线性模型回归法[18-21]。删除法主要是不考虑缺失数据对整个数据集的影响,这个方法主要适用于数据重要性较低且缺失数量较少,该方法会对计算结果造成一定的影响。插补法就是将缺失的数据进行估计插值,可以分为单点插值和多重插值,该方法要求数据相关性较大。线性回归法是利用统计中回归分析,确定两种及以上变量间相互的定量关系[22],可以将缺失数据最大程度构建出来。相比删除法和插值法,该方法准确率更高,更适用于常态缺失数据的构建,上述各种方法在相关领域已经得到广泛应用。

2 温度与应力的相关性分析

根据网安中心服役阶段顶部弦杆处某一监测点的应力与温度变化关系如图1所示,发现该测点的温度与应力波动有很明显的一致性。罗尧治[23]在国家体育场的温度与应力监测中发现大跨度空间钢结构的形态固定、外载荷不变时,对结构内部各杆件应力的首要影响因素是环境温度。在这种情况下,测点的应力和温度之间存在较强的相关性[24]。因此应力数据在监测过程缺失时,可以利用这种相关性来进行重构。

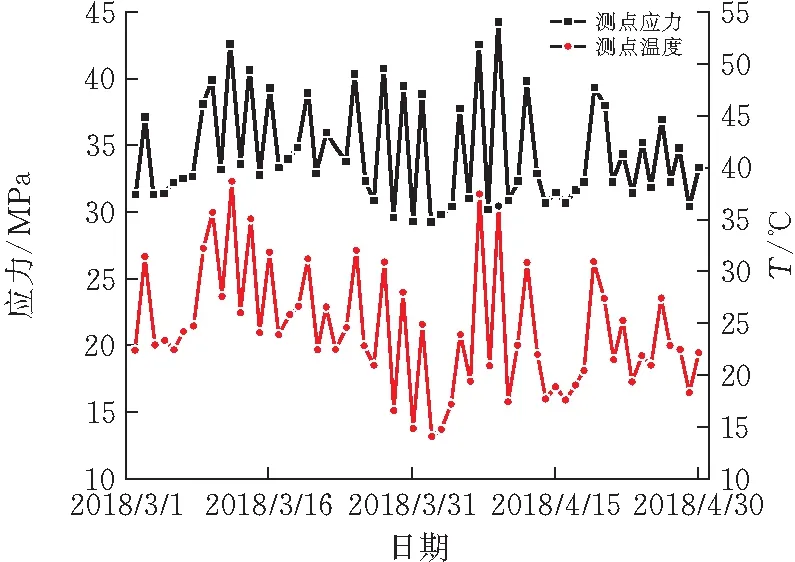
图1 监测点应力与温度长期监测数据曲线

根据上述发现,选取网壳结构中底部支座、中部杆件、顶部弦杆三个不同结构部位(图2)在2018年的监测数据,以应力数据为纵坐标,温度数据为横坐标,数据坐标点如图3所示。

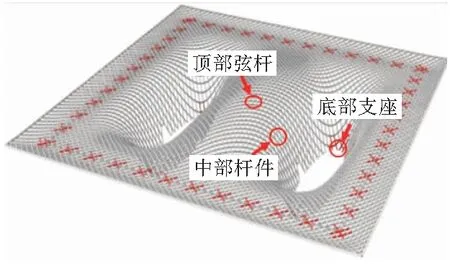
图2 不同结构部位示意图

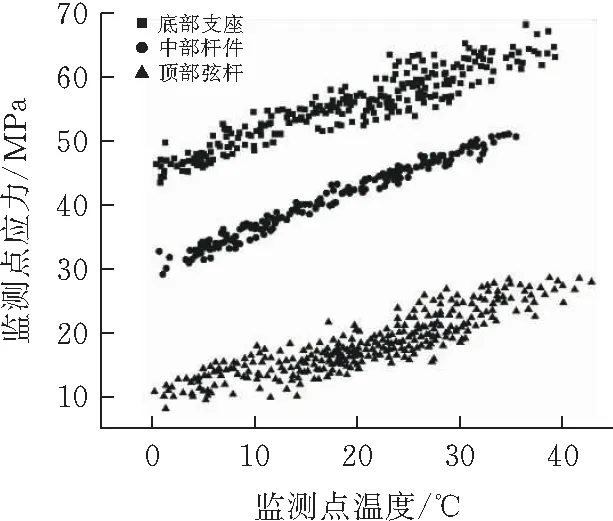
图3 监测点应力与温度相关关系

由图3可知,顶部弦杆、中部杆件和底部支座三个部位监测点应力与温度大致呈现较理想的线性相关关系。因此可以利用线性回归方法来拟合其线性关系。

对于一元线性回归,令y为监测点应力数据,x为监测点温度数据,则有一元回归拟合方程:

y=θ0+θ1x

(1)

式中:θ0,θ1是待求回归参数。

令拟合方程直线与真实数据值的偏差为

γi=yi-(θ0+θ1xi)(i=0,1,2,…,n)

(2)

设监测数据有n组,当各偏差的平方和L最小时,一元线性回归的拟合度最好。

(3)

按照极值原理,要使L最小,分别对式中θ0,θ1求偏导,令其偏导等于0即:

(4)

(5)

整理得:

(6)

(7)

由上式即求解出回归参数θ0,θ1。得到一元回归的拟合方程。

数据间的线性相关可以用相关系数R来衡量:

(8)

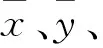
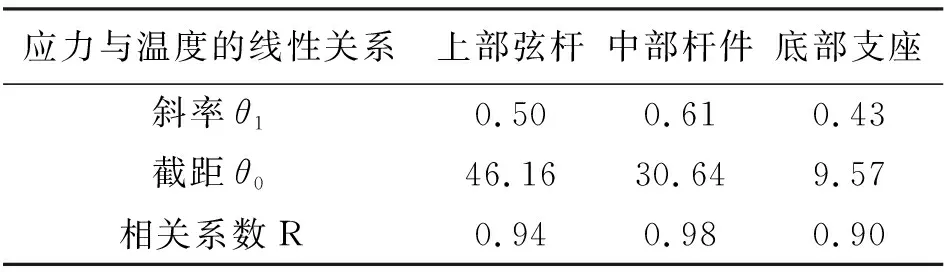
表1 监测点的应力与温度

根据表1绘出不同部位监测点应力与温度的线性关系如图4所示。

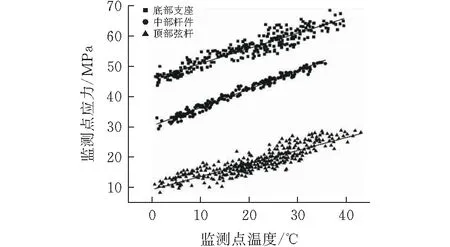
图4 不同部位监测点应力与温度的线性关系

图4横坐标表示监测点的温度数据,纵坐标表示监测点应力数据。图中可以看出,空间钢结构不同部位监测点的应力与温度之间具有十分理想的线性关系,相关系数均达到0.9以上。因此可知监测点应力和温度之间具有线性关系,可利用此线性关系重构缺失的应力数据。

3 温度场的影响分析

对结构温度的影响主要来源于日照场,网壳结构中顶部弦杆的温度受日照场影响最大。本文选取昼夜温差较大的8月份顶部弦杆某测点(监测位置如图2所示)的监测数据,不同时间段监测点温度与应力拟合直线如表2所示。

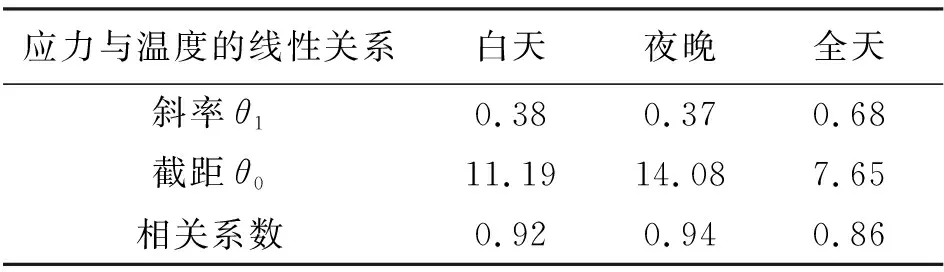
表2 不同时间段监测点温度与应力拟合直线

根据表2绘出不同时间段监测点应力与温度的线性关系如图5所示。

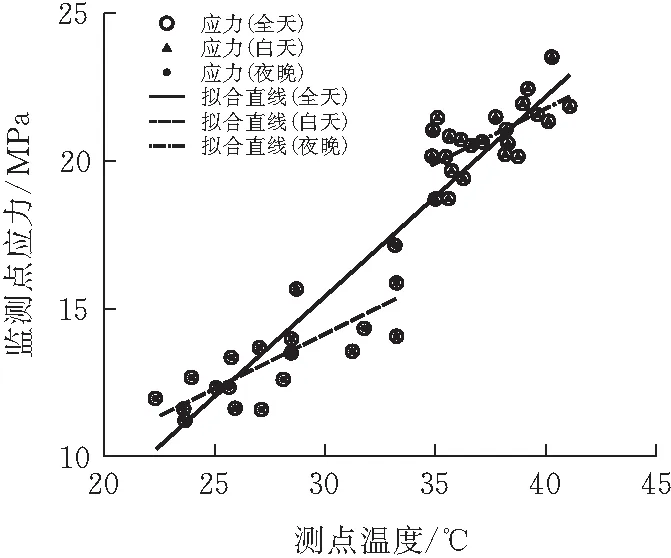
图5 监测点应力与温度关系

由图5和表2可知,监测点温度和应力具有线性关系。受日照的影响导致结构外层温度较高,内层温度较低,白天结构的温度场呈现非均匀状态,而夜晚时结构温度场相对均匀。因此在相同温度下,同一测点的监测数据在日间和夜间不等的。此时若不对白天和夜晚的监测数据进行区分,直接进行线性回归拟合,会产生较大的拟合误差,不同数据采集时间的重构误差如图6所示。

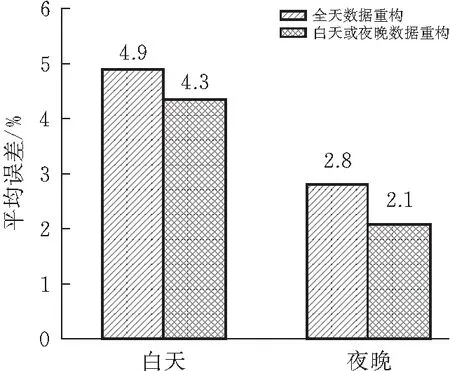
图6 不同数据采集时间的重构误差

由图6可知,对于白天数据,用全天的数据回归拟合的平均误差是4.9%,仅白天数据进行拟合下平均重构误差是4.3%,降低了0.6%。对于夜晚数据,平均重构误差从全天数据的2.8%,下降到仅夜间数据拟合的2.1%,下降了0.7%。对白天和夜间数据分别回归拟合,相较于对不区分白天和夜晚一起回归时,对缺失数据的重构精度能进一步提高。因此可以得出结论,不同温度场会导致测点数据之间的相关性不同。基于温度相关性对缺失的应力数据进行重构时,为保证数据重构的精度,对白天和夜间缺失的数据应分别进行拟合和重构。

4 缺失数据重构

由1.1节可知,离散型缺失和连续型缺失是空间钢结构健康监测中主要数据缺失类型。因此,本节将重点研究上述线性回归法在这两类不同缺失类型下的数据重构效果。

表3为顶部弦杆应力在某个时间段内的监测数据。

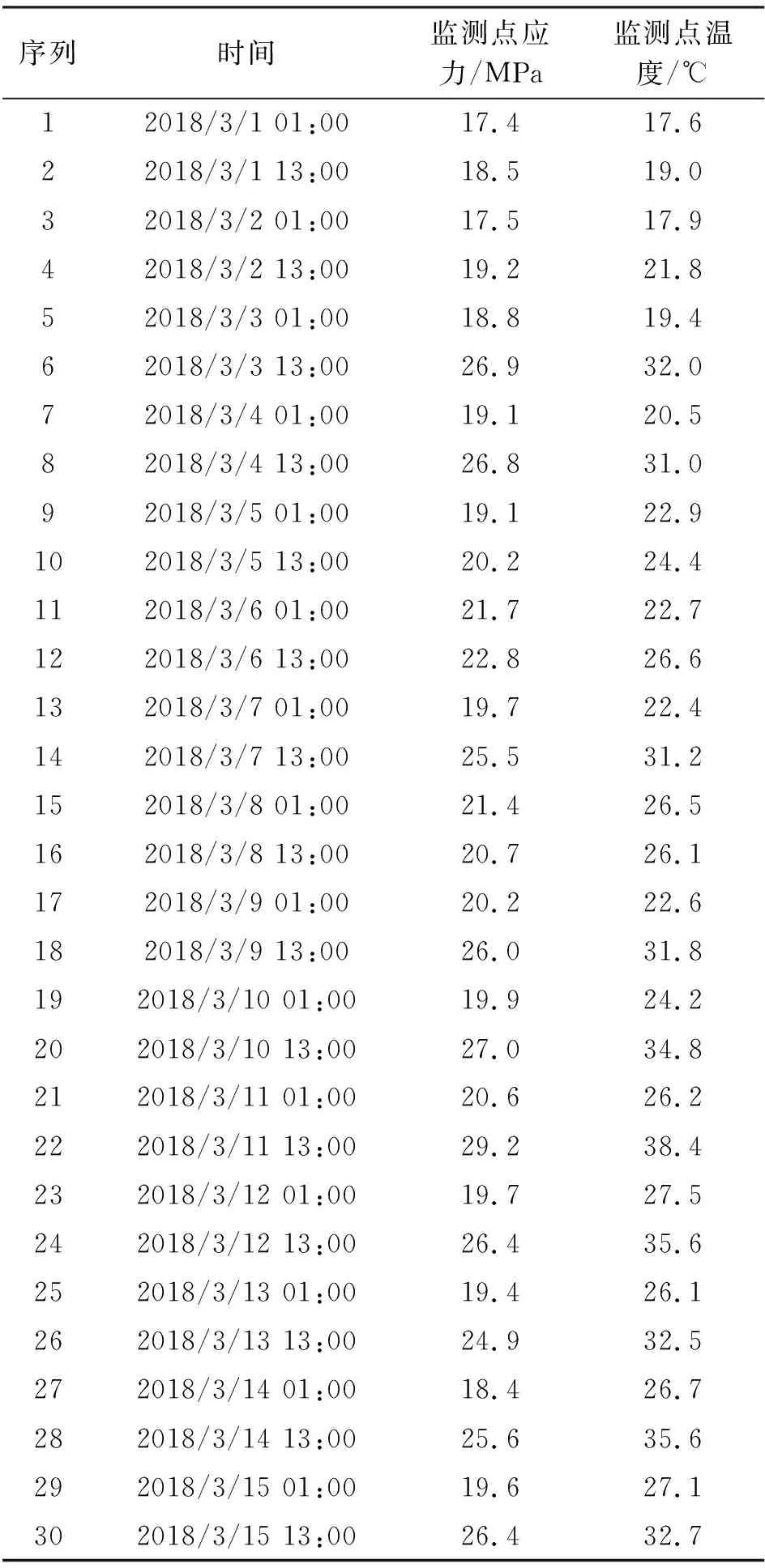
表3 监测点的监测数据

从表3节选3月1日到3月10日中序列为2、5、8、11、13、15、18、20的8个数据为离散型缺失应力;节选3月12日到3月15日中8个数据为连续缺失应力。采用该测点在2018/3/1至2018/3/15真实应力数据进行线性回归法重构曲线如图7所示。离散应力重构误差范围在0.7%～7.6%;连续应力重构误差范围在0.4%～7.1%,重构误差均在工程监测可以接受的精度范围内。

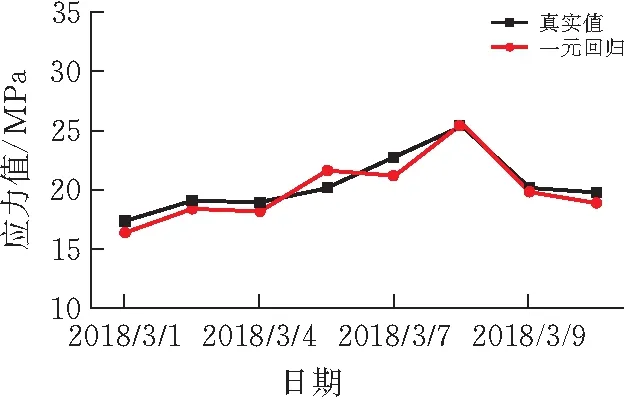
(a)离散型缺失

5 不同缺失率的数据重构效果

在实际监测过程中某监测点数据缺失的数量是随机的,为确定线性回归法适用的数据缺失率范围,本节研究监测数据在不同数据缺失率下的重构效果。

随机选取某监测点采集的150个数据,采用前文的方法进行线性回归重构。不同重构误差随缺失率变化如图8所示,截取其中部分真实数据与重构数据绘制曲线如图9所示。

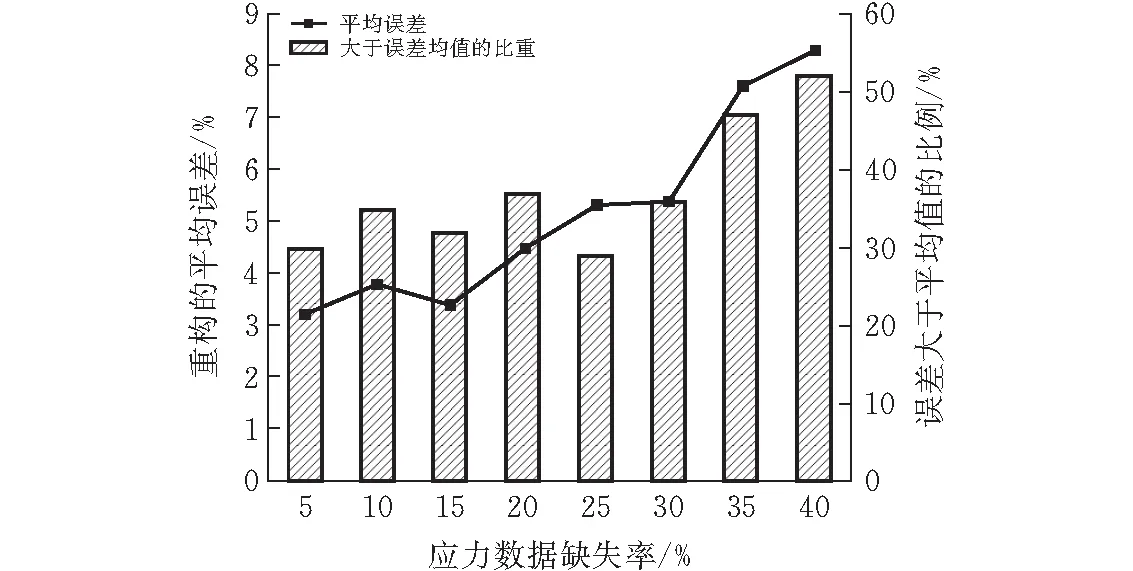
图8 基于温度相关性的重构误差随缺失率的变化

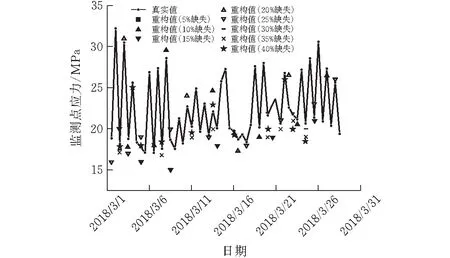
图9 基于温度相关性的真实值曲线与不同缺失率下的重构数据点

由图8可知,当缺失率在30%以内,平均相对误差在5%左右,当缺失比例达到35%时,平均误差上升较大,且重构误差高于平均误差值的占比也明显大于缺失率在30%以内,即此时重构的平均误差较大。同时由图9可知缺失率超30%时重构值与真实值偏离程度也增大。因此为使得平均重构误差以及大误差数据比例均达到所需要求。采用温度相关性时,待重构应力数据的缺失率应控制在30%以内。

6 结束语

本文通过线性回归法对大跨度钢结构健康监测中应力缺失数据的重构方法以及该方法的重构效果的适用性进行了分析。

监测数据表明:1)当数据缺失率控制在30%以内时,重构缺失应力数据与实测数据的平均误差小于5%;2)空间钢结构不同部位监测点的应力与温度之间相关系数均达到0.9以上。

因此,改进线性回归法能够适用于大跨度钢结构数据缺失的重构,提高了监测数据的可靠性,整体来看应力缺失数据重构误差均在工程监测接受精度范围内,为钢结构健康状态的综合评价奠定基础。