基于SIQR的新冠肺炎疫情动态传播模型研究

钞寅康, 龚立雄, 雷彬文

(湖北工业大学机械工程学院,湖北 武汉 430068)

新型冠状病毒肺炎是一种传染性很强通过呼吸道传染的疾病,基于新冠疫情的发展趋势,目前主要从两方面进行专业领域的研究,一种从疫情的控制角度,主要针对病毒的平均潜伏期以及基本再生数[1-3];另一种则是基于SIR模型以疫情传播的建模和预测为主[4-5]。其中,阿曼多等利用SIR模型预测新冠肺炎疫情的演变,预测的数据与具体病例数据有很好的拟合。任中贵提出了基于SIR模型的COVID-19疫情数据分析,其中感染率和移除率这两个重要参数的拟合结果说明及时采取封城等防疫措施对医疗救助能力的提升十分重要。或者采用SEIR模型进行数据拟合[6-7],然后进行适当的假设来推测疫情后期发展趋势,为疫情防控提供参考。SEIR模型相当于在SIR模型的基础上增加了传染病的潜伏期。赵成珍[8]在文章中对SEIR模型改进为三阶段模型然后对现实数据进行拟合;丁振华[9]提出了一种新的新冠肺炎传播非线性动力学模型;刘建国[10]在基于空间交互模型的基础上同时构建SEIR模型;董章功[11]提出了一种基于传统的传染病动力模型SEIR和差分整合移动平均自回归模型ARIMA构建的SEIR-ARIMA混合模型;以上模型都在SEIR模型基础上有所改进。但是SIR模型和SEIR模型二者均不能完全适用于湖北武汉的疫情发展的实际情况,考虑到2020年1月23日采取封城措施,对感染者进行隔离,在模型中增加隔离者提高模型的仿真水平,提高仿真结果与实际疫情的拟合度,给疫情防控提供更有价值的参考。

在上述背景下,本文基于系统动力学分析,构建了新冠肺炎疫情扩散的SIR模型,并在传统的SIR模型上进行改进和优化,改进为SIQR模型。最后,以武汉疫情为数据样本,使用改进后的SIQR模型进行仿真建模实验,并通过实验寻求预防和控制新冠疫情传播的方法。结果表明:该模型能有效地复现新冠病毒传播演化过程,为重大公共疫情的预测与防控提供指导依据。

1 SIQR模型与方法

1.1 SIQR模型构建

本次疫情传播迅速与传染病研究中SIR模型的特点相类似,但SIR模型在此次疫情中并不完全适用。以往的疫情没有如此果断且迅速的采取大规模隔离措施,因此本文在SIR模型的基础上增加隔离人群进行改进,使用SIQR模型进行有限区域内的疫情传播演化仿真。

改进后的SIQR模型中,治愈的传染个体拥有免疫抗体,设传染率(感染系数)为β,恢复率(恢复系数)为γ,SIQR模型状态转换图如图1所示。

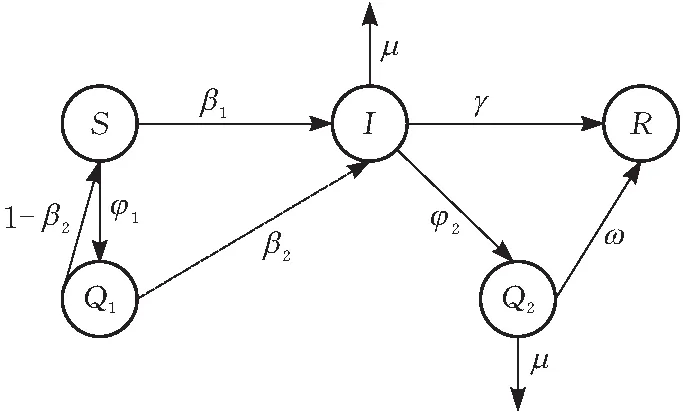
图1 SIQR模型状态转换图

SIQR模型将有限区域内的人口分为以下四类:1)染病者i(t),t时刻已被感染且具有传染力的人数;2)易感者s(t),t时刻还未染病但可能被传染的人数;3)隔离者q(t),t时刻已被进行隔离措施的人数;4)恢复者r(t),t时刻已从染病者中移出的人数。设总人口为N(t),则有N(t)=s(t)+i(t)+q(t)+r(t)。

1.2 SIQR模型假设

SIQR模型基于以下四个假设:

1)假设感染者的传染能力较强,但凡与易感染者接触就有被感染的风险。假设易感染总数为s(t),在t时刻单位时间内,被病人感染的比例系数为β,那么βs(t)i(t)就表示在t时刻内被病人传染的人数。

2)假设人口基数不变,忽略人口的流动、死亡和出生等种群动力因素。即N(t)≡K。

3)假设易感者和感染者分别按一定概率Ψ进行隔离,在t时刻进行隔离的人数为φ1s(t)+φ2i(t)。

4)假设病人数量与从染病者中移出的人数在t单位时间内成正相关,且相关系数为γ,则单位时间内移出者的数量为γi(t)+ωq2(t)。

基于以上四个假设条件,感染机制如

(1)

由以上所有假设可知:若对感染者和易感者采取一定的隔离措施,感染者的恢复率增长为γi(t),易感个体的下降率为βi(t)s(t),感染者的增长率达到β1i(t)s(t)+β2i(t)q(t)-γi(t)。易感者从患病到移出的过程可用微分方程表示,如

(2)

1.3 SIQR模型参数设定及应用

1.3.1模型参数设定本案例基于系统动力学进行SIQR新冠疫情传播演化仿真,时间以离散数据的形式表示,分别使用易感者、感染者、隔离者和治愈者来区分个体的不同状态。隔离者又分为在家隔离者和医院收治隔离者两类群体。移出者分为感染死亡/隔离死亡/治愈者。感染者区分为入院治疗和重症隔离两种情况,两者将不同程度地影响死亡人数和治愈人数。模型公式及参数设定如表1。

表1 SIQR新冠疫情传播演化模型的相关计算公式

1.3.2SIQR模型的验证本文数据来源于中国湖北省卫生健康委员会官网(http:∥wiw.hubei.gov.cn)公布的湖北省2019年12月31日—2020年5月的疫情数据进行实验。然后基于SIQR模型对新冠疫情传播演化机理进行仿真和推演,可以得到封城前后的数据参数如表2所示。

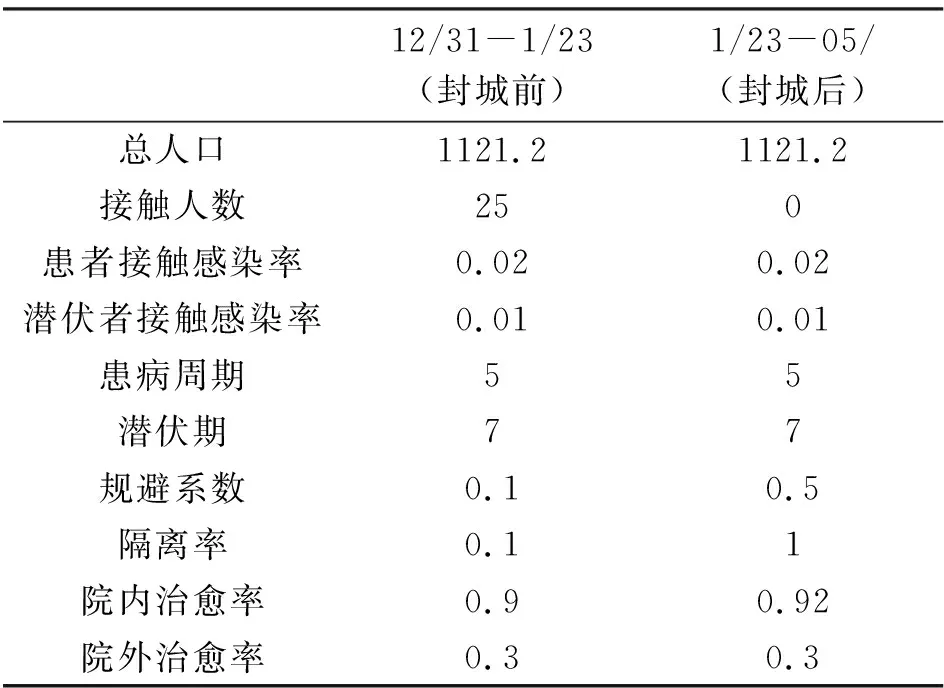
表2 封城前后数据

相比于传统SIR模型,增加了潜伏期、规避系数、隔离率等参数。经仿真求解,得出封城前和封城后治愈人数、感染人数和死亡人数三者的曲线,如图2、图3所示。

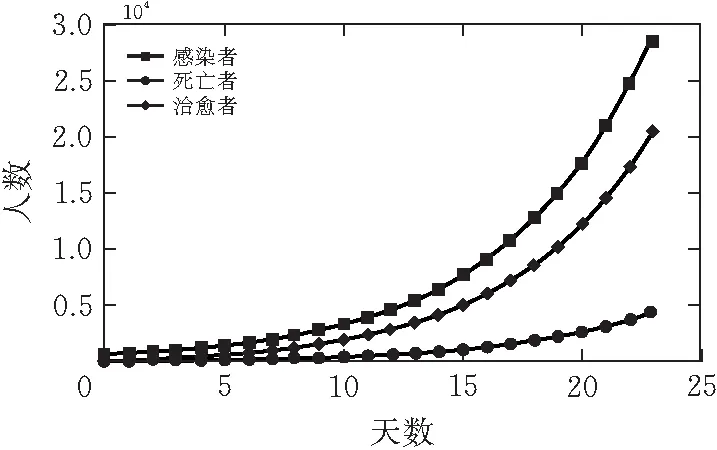
图2 封城前曲线

通过图2、图3的分析,可以将我国新冠疫情累计确诊数量的拟合情况大致分为三个阶段:

1)第一阶段为 12月 31 日～1 月 23 日,疫情初期防控力度小,传染途径广,感染人数呈指数增长,并产生了大量的二、三代感染者,但此时医院资源供给相对充足,感染者治愈率较高。

2)第二阶段1月 23 日～2 月 6 日,随着防护意识及政府管控力度增加,聚集感染事件减少,治愈系数已经大于感染系数,感染人数达到峰值后迅速下降,但由于前期大量感染者的涌入造成医疗资源陷入匮乏,导致治愈者人率并未达到峰值,且死亡人数还在增长。

3)第三阶段 2 月 6 日后,封城物理阻断了传播途径,治愈人数呈指数增长,感染者人数逐渐趋近于零,死亡人数曲线已趋于平缓。

本文模型中考虑到武汉及时的“封城”行为,以及政府在多方面实施强有力措施,使新冠肺炎传播在时间、空间上具有明显的异质性,而本次仿真中得到的指数增长,可以推论是因为病毒平均潜伏期较长,在有限区域内对特定人群(中老年人等免疫力较差的群体)的感染性强,导致疫情爆发速度快,医疗体系在短时间内不堪重负、瘫痪所造成的。

2 多因素的影响研究与讨论

为了更加贴近武汉疫情传播真实现状,进行有效模型的构建,本文在模型构建过程中基于政府以及群众不同的角度在疫情发展的不同阶段,采取的不同措施进行分析。通过添加规避系数以及隔离率两大因素,主要体现政府采取措施的力度以及群众防疫意识的强弱;通过添加病毒潜伏期和疫苗覆盖率两大因素,主要从病毒分析,体现病毒对医疗以及社会经济的影响。

2.1 规避系数对疫情传播演化的影响

规避系数的定义是将该地区各方面防疫措施对新冠肺炎疫情扩散程度的影响引入模型,是对该地区的政府是否采取措施,措施力度是否严厉,以及医疗资源,人口素养等多方面因素的综合。

武汉封城举措,影响规避系数,图4中规避系数越大,感染者人数越少。其中分为三个小阶段:

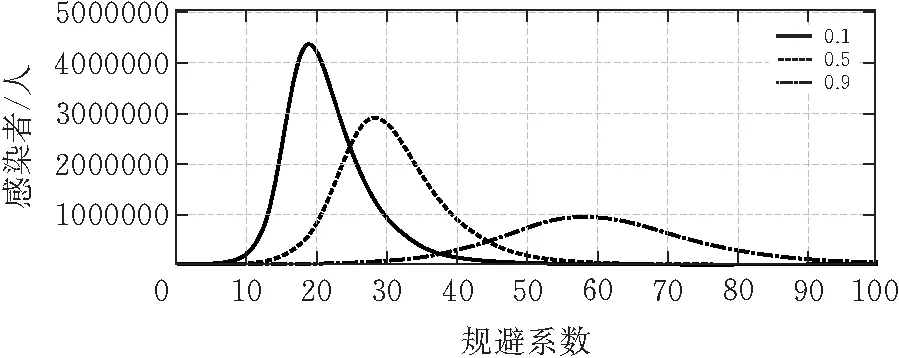
图4 封城后规避系数不同对感染人数的影响

1)0.1-0.4:视为该地区没有采取防疫风险等级制度的相关措施,区域内人群活动自由,频繁发生交叉感染,隔离点缺乏,患者无法及时得到治疗和隔离。疫情管控呈现出失控的态势。

2)0.5-0.7:该地区采取了对应防疫风险等级制度的相关措施,内防扩散、外防输入,在疫情爆发过程中及时隔离了二、三代感染者以及其密切接触者,并及时保障了足够的医疗资源。

3)0.8-1:该地区在发现疫情时及时进行了严格的隔离措施,人口都有较高的防控素养,并配有足够的医疗资源保障,疫情在该地区几乎很难爆发。

2.2 隔离率对疫情传播演化的影响

本模型中,隔离率不同时对感染者数量的影响如图5所示。

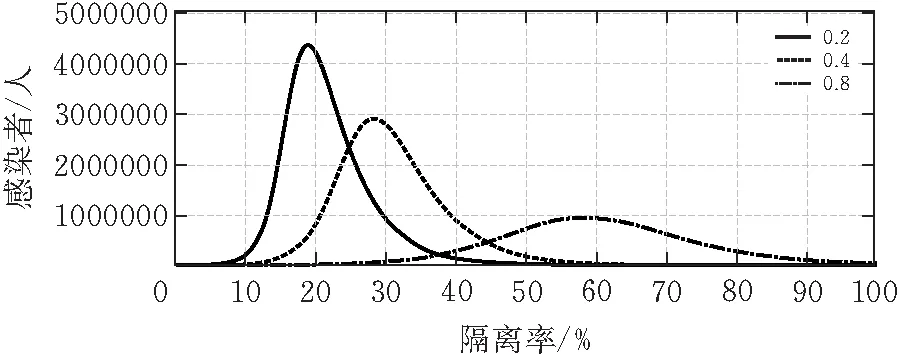
图5 隔离率不同时对感染者数量的影响

由图5可知,隔离率对疫情扩散程度的影响至关重要,隔离率越高,感染者人数越少,隔离率的提高能有效遏制疫情传播,但会给医疗体系带来巨大负担,从而造成较晚的峰点到来和较长的疫情防控时间,给社会经济发展和人们健康造成沉重打击。

2.3 平均潜伏期对疫情传播演化的影响

本模型在计算感染者人数的参数时,将本次疫情备受关注的新冠肺炎潜伏期引入模型,发现当病毒在区域内人群当中平均潜伏期不同时,会造成不同的疫情扩散情况,如图6所示。

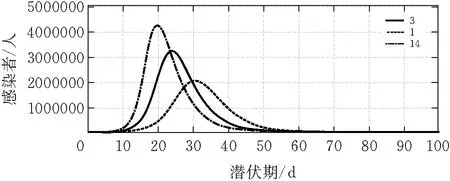
图6 潜伏期不同时对感染人数的影响

由图6分析可知,当其他参数相同时,病毒潜伏期越短,感染者数量峰值越低,但峰点到来较慢,疫情持续时间更长,对地区影响更持久;当病毒潜伏期越长,感染者数量峰值越高,但峰点到来较快,疫情持续时间更短,对地区造成短时间内较大的冲击性影响。

2.4 新冠疫苗接种对疫情传播演化的影响

研究疫苗覆盖率因素过程中,将已经接种疫苗设定为免疫人群,SIQR模型中易感染者人数会除去已经接种疫苗人数。例如,当接种疫苗率为20%时,易感染者人数在原先的值=总人口-感染者人数基础上除去接种疫苗的人数即20%的总人口。易感染者人数=((总人口-感染者人数)-20%总人口),规避系数变为0.3。

当疫苗覆盖率为0%、20%、40%、60%、80%时,感染者,易感染者、治愈者的人数变化曲线如图7-9。

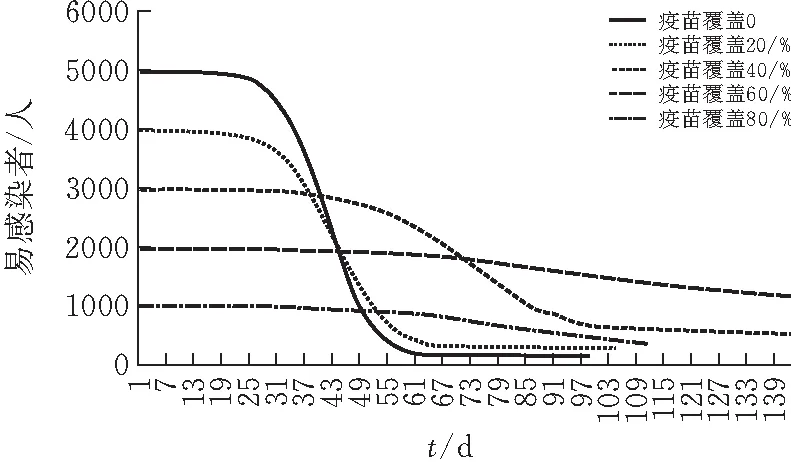
图7 易感者趋势

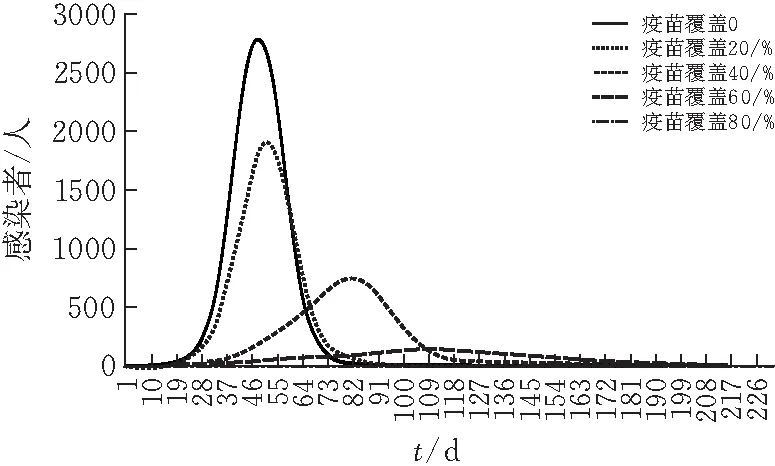
图8 感染者趋势

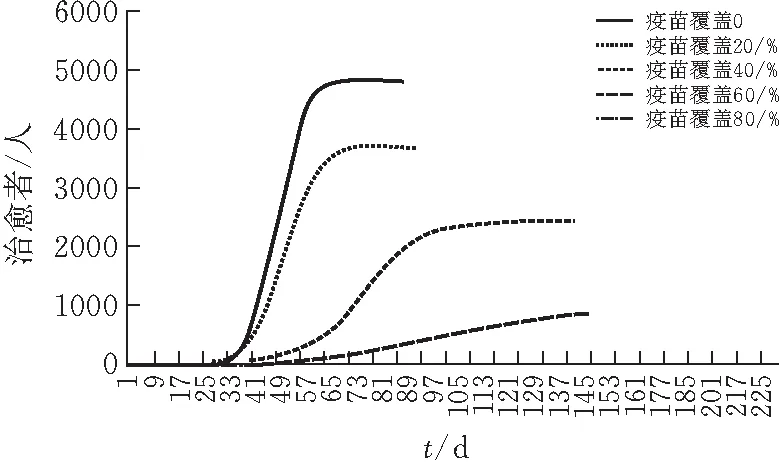
图9 治愈者趋势

基本传染数在流行病学上是指在没有外力介入并且所有人都没有免疫的情况下,某种传染病的感染者会把疾病传染给他人数量的平均数。

若β<1,传染病会逐渐消失;

若β>1,传染病会以指数方式散布成为流行病;

若β=1,传染病会成为地方性流行病。

在疫苗覆盖率的基础上基本传染数公式改进为:即当<1时传染病会逐渐消失,其中新冠的基本传染数=3.28,则当P>0.7时传染病会逐渐消失结束疫情。

从国药集团公布的数据来看疫苗的保护效力为79%,疫苗覆盖率P是在疫苗保护效力为100%的情况下得出的,因此要达到90%的疫苗覆盖率才可以形成人群免疫屏障阻断疫情再次发生。

2.5 模型对比

为进一步验证本模型的优越性,本文以疫情期间一、二月部分数据为数据集,分别使用SIR、SEIR以及本文的SIQR分别进行仿真预测,实验结果如表3、图10所示。

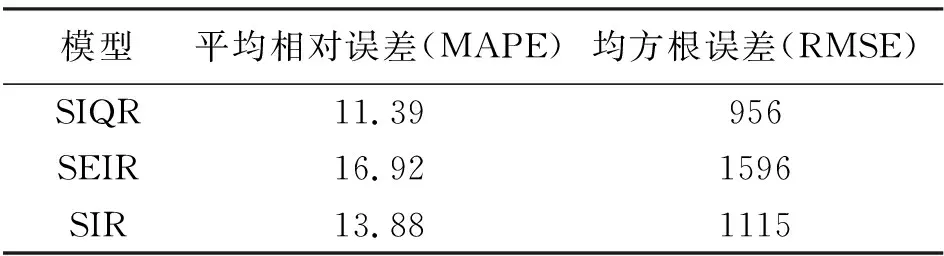
表3 误差对比 %

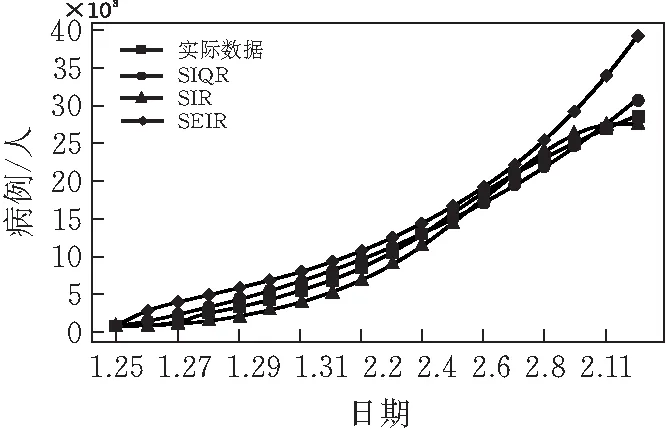
图10 模型拟合效果对比

通过对图10、表3的观察,可以发现三种模型的拟合趋势都与疫情发展趋势相同,但本文模型拟合效果明显更好。并且通过数据对比可知,本文模型相较于初始SIR模型,MAPE值缩小了2.49%,RMSE值缩小了159;相较于SEIR模型,本文模型的MAPE值缩小了5.53%,RMSE缩小了640,进一步体现了本文模型的优越性。

3 结论

本案例在SIR 模型基础上增加潜伏期、感染率、规避系数、隔离率、治愈率等参数进行改进和扩展,并以武汉疫情数据为例,对有限区域内新冠肺炎疫情扩散机理及感染者、治愈者、死亡数量进行了仿真。最后通过与其他模型的对比,证明了本文模型的优越性,得出结论如下:

疾病的传播机制在现有感染者死亡或康复的数量与新感染者数量相等的时间点发生变化。当感染者恢复正常的数量大于新感染个体数目时,疫情规模将减小;当规避系数大于等于0.5时对疫情扩散有明显的遏制作用;当病毒潜伏期大于等于4 d时,会造成疫情剧烈增长;高隔离率可以降低感染者数量,但是对医疗系统有较大负担;接种新冠疫苗是阻断病毒的最佳方式,疫苗覆盖率要达到90%才能形成人群免疫屏障阻断疫情。