“矩阵理论”课程分层次混合式教学模式探索

杨云龙

（大连海事大学理学院 辽宁 大连 116026）

1 研究背景

全面落实以学生为中心是贯彻执行党的二十大精神和全国教育工作会议精神，提高人才培养质量和实现三全育人的重要举措，在培养新时代接班人等方面具有重要的战略意义。以学生为中心的教学就是在教学中将学生作为教学环节的中心，在教学中将学生当作主要的参与者，将学生作为研究学习的对象，促进学生人格的培养、综合素质的提高、分析问题和解决问题能力及学习能力的提升。

矩阵理论作为研究生数学公共基础课，不仅是大学本科线性代数课程的延续，而且是模式识别、图像处理、人工智能等实际应用领域的数学理论基础，在课程体系中承载着拓宽学生视野，树立学生科学精神的重要作用。通过课前的问卷调查，结果反映出学生对线性代数等大学数学知识的掌握程度差别较大，学生对大学数学知识的掌握参差不齐，要解决上述问题，同时体现课程的综合应用性和知识的高阶性，与其他课程协同实现育人目标，分层次教学是必然选择。受学时限制，传统课堂的分层次教学不易实现，而混合式教学可根据知识点的难易程度，通过网络资源对知识进行模块化处理，为不同知识层次的学生搭建不同难度和不同主线的课程内容，因材施教，不仅体现课程的高阶性，而且符合国家的教育数字化战略。

美国实用主义教育家杜威的“以儿童为中心”是“以学生为中心”教育理念的起源。2011 年华中科技大学校长李培根在《以学生为中心的教育：一个重要的战略转变》中明确提出“以学生为中心”的教育，关乎大学的核心理念，关乎大学精神与文化，关乎学校未来发展战略。

当前，以学生为中心的混合式教学在数学研究生课程中的实践研究甚少，多集中于本科阶段的公共基础课程[1-10]和数学专业课[11-12]，分层次教学模式在数学线下课程，尤其本科阶段的高等数学等数学类公共基础课中进行了相当程

度的实践探索，参见文献[13-16]。在如化学[17]和计算机[18]等具有实验操作的学科，分层次混合式教学模式也已得到尝试。文章从研究生的矩阵理论课程实际现状出发，探索以学生为中心的混合式教学模式，不仅满足自身课程建设以及完成研究生培养目标的需要，而且对其他研究生数学公共基础课也有一定借鉴意义。

2 “矩阵理论”改革举措

本文基于以学生为中心的教育理念，重塑大连海事大学研究生数学类公共基础课“矩阵理论”课程框架内容，构成多层次多目标的学习任务，通过“课前—课中—课后”教学过程闭环，融入课程思政内容，三位一体地实现全面育人的培养目标。

结合学生的专业特点，修订课程内容，尝试将授课内容分成A（基础）、B（提高）和C（拓展）三个层次，探索与知识点对应的课程思政元素，具体实施细节包括：

2.1 课程内容分级

课程中的A（基础）层次知识点包括：矩阵的基本运算（包括矩阵的加法、数乘、乘法、转置，方阵的行列式、逆矩阵、迹、共轭矩阵、矩阵的分块）及性质，方阵的特征值和特征向量，正规矩阵，正定矩阵和半正定矩阵，正交矩阵，酉矩阵，Hermite 矩阵，矩阵的Smith 标准形，向量范数和矩阵范数，行列式因子、不变因子、初等因子，线性空间的定义与例子、线性空间的维数、基与坐标，子空间及其运算（包括子空间的和、交、直和），线性变换、正交变换、对称变换，实内积与欧氏空间，矩阵的三角分解（包括LU 分解、Choleskey分解、QR分解）与满秩分解，矩阵幂级数与矩阵函数。

课程中的B（提高）层次知识点包括：矩阵的谱分解、矩阵的奇异值分解、Reyleigh 商与圆盘定理，不变子空间，核空间和像空间，复内积与酉空间，向量或矩阵求导，因式分解定理，零化多项式和最小多项式，矩阵的Jordan标准形，矩阵函数与微分方程组的解，广义逆矩阵及其应用。

课程中的C（拓展）层次知识点包括：两气象场交叉相关系数计算，声学系统的动态分析，电网薄弱环节辨识的数据表征，奇异值分解在信号处理中的应用，矩阵旋转与特征提取，数据降维与主成分分析。

2.2 思政元素融入

针对不同层次的知识内容，确立以培养数学思维、树立科学精神、抱有家国情怀、欣赏数学之美、探索生活实践、掌握哲学思辨为导向的课程思政元素融入方向，具体实例包括：

①矩阵理论以矩阵为主要工具，借助线性空间和线性变换等数学概念为工程方面的实际应用提供描述语言，将“工欲善其事必先利其器”的名句体现得淋漓尽致，展现了数学思维的系统性和全局意识。

②矩阵理论中的一个重要研究主题——方阵的特征值和特征向量，矩阵概念提出伊始就一直活跃在理论研究和实际应用之中，经过不同时期数学家的深入思考，从单纯求特征值和特征向量，逐渐发展到直接从矩阵本身的元素特征出发而对矩阵进行特征估计，对方阵的特征值和特征向量的不断探索反映了其不屈不挠的科学精神。

③在矩阵理论的发展历程中，也有许多中国科技工作者的身影。国际著名数学家华罗庚先生是矩阵几何学等诸多领域相关研究的创始人和开拓者。中国科学院郭雷院士解决了最小二乘自校正调节器的稳定性和收敛性这一国际著名难题。他们的事迹无不激励一代学子投身国家建设，努力将科研成果应用到祖国大地上。

④矩阵理论中的研究对象出现在实际生活中的许多场景中，如港口的货运调配与最小二乘法相联系，电网的薄弱环节辨识与随机矩阵密切相关，人工智能中滤波与矩阵的卷积运算紧密相连，生活中的指纹识别和人脸支付等许多应用场景都有矩阵特征提取的身影。这些矩阵理论在生活中的应用无不体现了数学之美。

⑤与矩阵论相关的张量分析与外代数同物理学家探究广义相对论的工具不谋而合，体现了哲学中的事物的统一性原则。

在课程资源拓展方面，结合自建课程资源内容，筛选优秀的网络资源，拓展学生的课后自主学习资源，引导学生独立思考，具体实施细节包括：

2.3 深化过程性考核机制

在过程考核过程中，结合研究生的专业情况和前期问卷调查中对大学数学的掌握程度，对学生进行分组，增加小组协作作业，要求根据组内学生的研究方向，进行与课程相关内容的学习经验分享，同时在过程性考核中增加文献综述的小作业，在加深对矩阵理论基本概念、基本原理理解的过程中，又能进行文献筛选、文献阅读、写作规范等学术方面的训练。

2.4 前沿应用和优质学习内容推送

精选鄂维南院士《机器学习的数学理论》和中国运筹学会《运筹学千里纵横论坛》中涉及本课程内容的相关通识报告，拓宽学生的数学视野，加深对矩阵理论相关知识的理解。推送与课程内容相关的优质学习内容，如哈尔滨工业大学严质彬老师的“矩阵分析”和斯坦福大学的公开课“应用线性代数”。

2.5 基于知识图谱的知识主线重组

通过对课程内容中的知识点进行分级，实现知识的碎片化，基于知识图谱形成理论与实际相连的新课程主线供学生学习。以主成分分析这一内容为例，在国内现有的矩阵理论通用教材中，在有限的学时内，都无法系统讲解到该部分，但实际上主成分分析的理论基础均碎片化地存在于矩阵理论的课程知识点中。要想掌握主成分分析，在大学数学阶段要了解协方差与协方差矩阵的基本内容，在矩阵理论课程的层面只需要掌握半正定矩阵、Reyleigh商、矩阵函数的求导法则这些内容。而主成分分析在数据降维、计量经济学等研究中均有广泛的应用。基于知识图谱的知识主线重组，不拘泥于教材章节结构内容，实现了对部分课程扩展内容的理解与掌握，丰富了课程内容，有效地体现了课程的高阶性。

3 建设情况与实践效果

经过两个学期的课程建设，完善了“矩阵理论”课程在海贝云和雨课堂平台上的课程内容搭建，已建设完成海贝云课堂8 个学习单元32 个必学模块，6 个选学模块，包括教学视频、授课课件、平时作业、期末复习、延伸阅读等内容，完成雨课堂资源包内图文、视频类内容共计9 章26 个学习单元及课程思维导图与配套习题库建设，为学生提供了不同程度的自主学习资源。

经过一个学期的实践教学，在不改变平时成绩占比且考题难度与考点相同的前提下，以学生的实际期末考试试卷成绩为标准，22—23（2）学期（改革学期）与之前的学生成绩数据相比，90 分以上优秀学生占比有一定程度提高，平均成绩较往年也有所提高，数据比对详见图1。“矩阵理论”课程的混合式教学实践踏出了以学生为中心的分层次混合式教学模式在大连海事大学研究生数学公共基础课建设的第一步，对其他数学类研究生课程也有一定的指导意义。

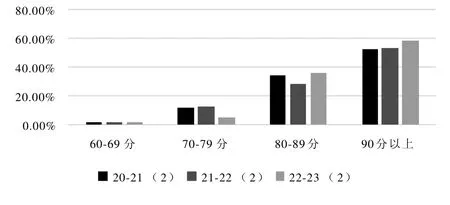
图1 改革前后学生成绩对比