某大口径火炮高平机平衡性能分析及优化研究

李仕轩，刘宁，王永河，康瑞霞，杨亮亮，何维真

(西北机电工程研究所，陕西 咸阳 712099)

近年来,为降低火炮质量,精简火炮结构,提高操炮轻便性,多能融合式组件越来越多地被应用于现代火炮设计中。火炮高平机有机融合了火炮高低机和平衡机两方特点,其结构紧凑,操作便捷,是多能融合设计的经典应用。

火炮高平机平衡性能是衡量火炮高平机设计的关键因素,平衡性能的好坏对于火炮高低调炮的轻便性和快速性起着重要作用[1]。国内外专家学者对火炮高平机设计开展了大量的研究工作,林通等[2]提出了一种高平机模型参数识别方法,并通过灵敏度分析,获得了对火炮起落部分运动影响较大的高平机参数;张训国等[3]研究了螺杆式高平机的工作原理,并建立了一种针对螺杆式高平机的优化设计方法;赵凡等[4]利用ADAMS建立了高平机作用下的火炮发射动力学模型,验证了高平机的工作性能;张柳怡等[5]将稳健优化方法引入到高平机参数设计中去,降低了高平机手轮力对温度变化的敏感度,提高了高平机的稳健性。综上所述,现阶段国内外专家学者对大口径火炮高平机性能的研究主要集中在螺杆式高平机性能分析、动力学仿真[6-7]等方面。尽管对液体气压式高平机的计算及优化设计方法的研究也进行了相关研究,但高平机主要设计参数对平衡性能的影响规律并未充分诠释,导致在后续设计过程中核心关键参数的优化存在一定缺陷,增加了设计优化算法的难度。

笔者依据火炮高平机设计理论与结构原理,建立了液体气压式高平机的不平衡力矩计算模型,系统分析了不同设计参数对高平机平衡性能的影响规律;并以某大口径火炮液体气压式高平机结构参数为基础,提出了一种基于遗传算法的高平机平衡性能优化设计方法,使得高平机各设计参数可在设计范围内快速寻优,进一步提高了液体气压式高平机的平衡性能。

1 高平机结构组成

某大口径火炮高平机为液体气压式高平机结构,具备高低机和平衡机的功能。采用左右对称布置,高平机的前支点通过油缸耳环和关节轴承与摇架相连,高平机后支点通过活塞杆上的叉形耳环和关节轴承与上架相连,具体安装位置如图1所示。

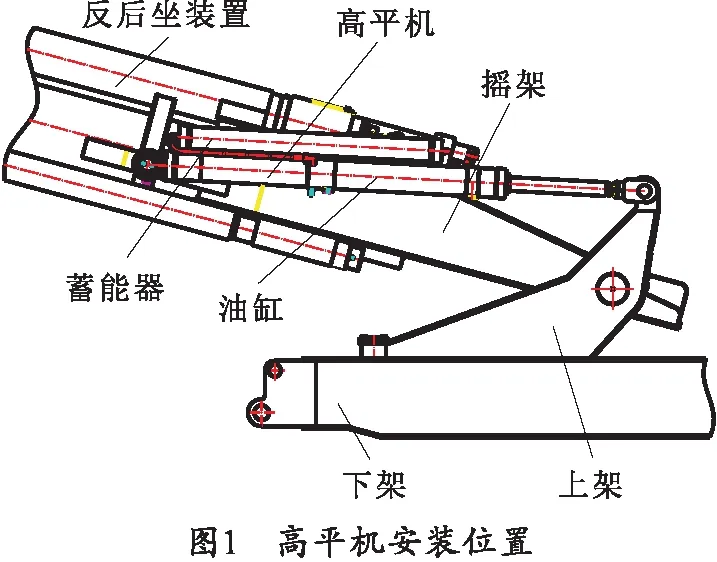
该型高平机采用多能融合设计思路,主体主要是由油缸及蓄能器组成,如图2所示。其中蓄能器采用气压式结构,具有质量轻、外形小、加工调整方便等一系列优势[8-9],蓄能器结构主要是由缸筒、活塞、前后端盖等组成,活塞两侧分别为蓄能器的液腔与气腔。高低油缸安装于蓄能器下部,主要由油缸筒、后活塞、隔环总成、活塞杆、叉形耳环等组成,隔环总成两侧分别为平衡腔与高低腔,高低腔活塞的两侧为高低机的前后腔,具体内部结构如图2(b)所示。

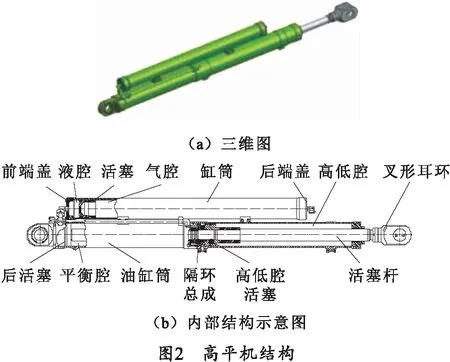
2 高平机平衡性能分析

2.1 工作原理分析

高平机平衡性能常用不平衡力矩的大小作为衡量指标。某大口径火炮高平机在工作时,通过火炮液压系统实现活塞杆的伸缩,从而使火炮起落部分可绕耳轴旋转,进而得到火炮的高低射角,并利用液压锁实现火炮射击时的自锁效果。高平机后活塞通过活塞杆与高低机的活塞相连,高低机的运动带动后活塞运动。平衡腔内注有液压油,通过相关油管与蓄能器的液腔相连,以此来实现后活塞运动带动蓄能器活塞运动,使蓄能器中的气体进行相应的压缩与膨胀,从而得到变化的平衡机力。

由上述工作原理及某大口径火炮起落部分的具体结构,可计算出火炮起落部分的重力矩Mk:

Mk=mkglkcos(φ-r0),

(1)

式中:mk为起落部分质量;g为重力加速度;lk为火炮质心到耳轴的距离;φ为射角;r0为0°射角时,起落部分重心到耳轴中心连线与水平线的夹角。

根据高平机的安装布置形式,可知高平机的具体传动三角形,如图3所示。其中a为高平机前支点位置,b为高平机后支点位置,两支点间的距离为Sφ。

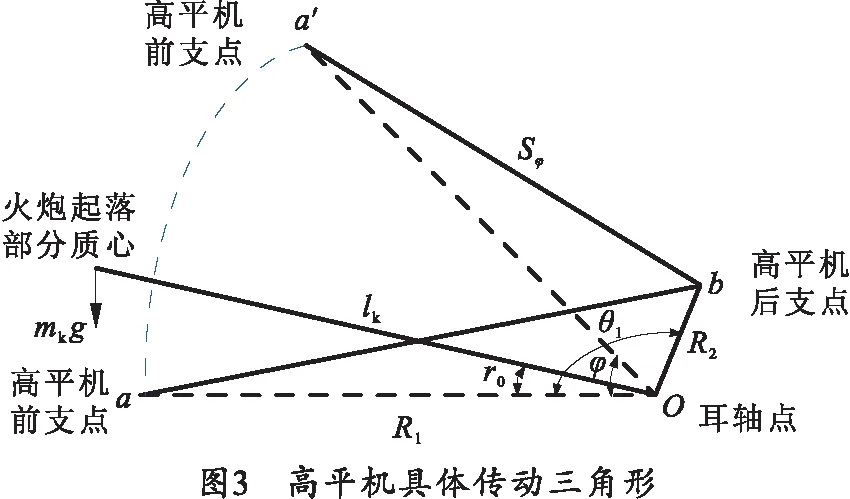
根据图解法,运用运动简图中的几何关系可得不同射角范围内的高平机两支点的距离变化关系:

(2)

式中:R1,R2分别为高平机前后两支点与耳轴之间的距离;θ1,θ2分别为射角为0°时,高平机后支点与前支点至耳轴连线与水平线之间的夹角,且θ2=0°。

由△a′Ob中的几何关系可得,此型高平机在任意射角的平衡力臂为

(3)

2.2 不平衡力矩计算

由于该型高平机采用气压式结构,平衡力主要由气缸内气体压力变化产生,根据气体压力计算公式可得不同射角下的高平机内部气体压力变化规律:

(4)

式中:Pφ为射角为φ时的气体的内部压力;Pmax为最大射角时的气体内部压力;Vφ为射角为φ时气缸内的气体初始状态容积;Vmax为最大射角时气缸内的气体初始状态容积;n为气体状态方程式指数,由于高平机工作时,气体压缩和扩张很慢,接近等温过程,故一般取n=1.05[10]。

根据高平机的内部结构可知其蓄能器的单侧气体容积为

(5)

式中:D为活塞直径;D1为活塞杆直径;h为气缸初始容积长度;

通过计算求得的气体容积和气体压力,可得高平机的抗力规律,即:

Fφ=2PφA,

(6)

式中,A为高平机后活塞工作面积。

因此,高平机的平衡力矩和不平衡力矩ΔM分别为

MF=FφSFφ,

(7)

ΔM=Mk-MF.

(8)

2.3 设计参数对高平机平衡性能的影响

为更加准确地分析高平机的平衡性能随设计参数的变化情况,根据提出的高平机不平衡力矩计算方法,分别考察高平机前支点与耳轴点的距离R1,后支点与耳轴点的距离R2,活塞直径D,活塞杆直径D1及初始压强P等主要设计参数对高平机平衡性能的影响规律。

此处以火炮耳轴点O为原点,取高平机的前支点与耳轴点的距离R1∈[1 860,1 960],后支点与耳轴点的距离R2∈[400,500],活塞直径D∈[90,110],活塞杆直径D1∈[50,60],初始气压P∈[8,9]。在改变其中的某一设计参数值时,保持其余参数不变,则可得到不同设计参数对高平机平衡性能的影响规律。

前支点与耳轴点的距离R1及后支点与耳轴点的距离R2的变化对高平机平衡性能的影响分别如图4和图5所示。

随着高平机前支点与耳轴点间的距离R1的不断增大,在15°～59°的常用射角范围内,高平机的不平衡力矩基本不变,可见高平机前支点与耳轴点的距离R1基本不影响不平衡力矩的大小,高平机平衡性能对前支点与耳轴点的距离R1变化并不敏感。相反,高平机后支点与耳轴点的距离R2变化可使高平机不平衡力矩数值产生较大变化。随着后支点与耳轴点间的距离R2的不断增大,高平机的平衡力逐渐增加,不平衡力矩先减小再反向增加。由此可以看出,相比高平机前支点与耳轴点的距离R1,高平机后支点与耳轴点的距离R2的改变对高平机的平衡性能影响更加显著。

活塞直径及活塞杆直径的变化对高平机平衡性能的影响规律分别如图6和图7所示。随着活塞直径D的不断增大,高平机所产生的平衡力矩也逐渐增加,导致不平衡力矩先减小后反向增大。相反,活塞杆直径D1的逐渐增大,导致高平机所产生的平衡力逐渐减小,不平衡力矩逐渐增大。与此同时,对比图6及图7可以看出,在直径变化量相同时,高平机不平衡力矩对活塞直径D的变化更为敏感。活塞直径D对高平机的平衡性能影响更大。

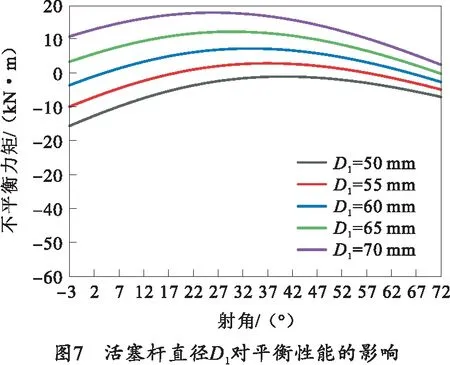
由于高平机产生的平衡力主要是由蓄能器气腔气体膨胀及压缩产生的,故高平机初始气压对其平衡性能也会产生重要的影响。此处选取初始气压范围为8～9 MPa,取值间隔为0.2 MPa,代入上述计算模型,即可得到初始气压对高平机平衡性能的影响,如图8所示。

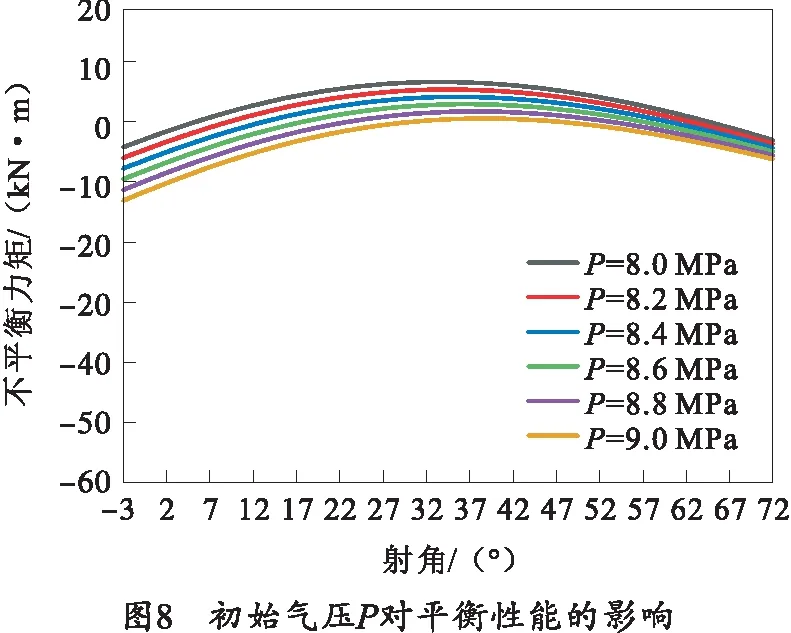
因此在进行高平机参数设计时,当以其平衡性能最优为优化目标时,应优先考虑其后支点与耳轴点间的距离R2,合理设置活塞直径D、活塞杆直径D1范围,综合考虑高平机初始气体压力P范围。

3 平衡性能优化设计方法

为进一步提升高平机的平衡性能,利用设计参数对高平机平衡性能的影响规律,选择合理方法对该型高平机进行平衡性能优化设计。由于笔者主要优化目标为高平机平衡性能,此处不考虑高平机特性对火炮初始扰动影响。

3.1 优化算法选择

目前,国内已有学者针对高平机的设计使用特点对其进行了部分优化设计,并未对其设计参数影响规律进行具体分析研究[3],导致其整体优化设计模型采用的算法较为简单,收敛性较差,无法确定为其优化参数是否为全局最优解。

遗传算法是现阶段一种高效的并行全局搜索方法,其源于自然选择和自然遗传机理,具有搜索覆盖面大、收敛速度快等特点,具备求得全局最优解的能力,常应用于复杂系统的优化当中[11-13]。其中选择、交叉和变异构成了遗传算法的遗传操作;参数编码、初始种群设定、适应度函数设计、遗传操作设计和控制参数设定5个基本要素构成了遗传算法的核心内容。遗传算法能够自身进行自我迭代优化,在自身系统内进行优胜劣汰,从而寻找到全局最优解。

基于此,笔者根据上述分析设计参数对高平机平衡性能的理论分析结果,利用遗传算法参数调整方便、快速收敛性强、计算全局最优解准确等特点,选择遗传算法作为此次高平机参数优化的核心优化算法,从而对其具体结构设计参数进行参数优化求解。

3.2 优化模型建立

根据上述遗传算法优化方法的计算原理及某大口径火炮液体气压式高平机的主要结构特点,利用MATLAB软件构建基于遗传算法的大口径火炮高平机的平衡性能参数优化模型,具体参数优化流程如图9所示。

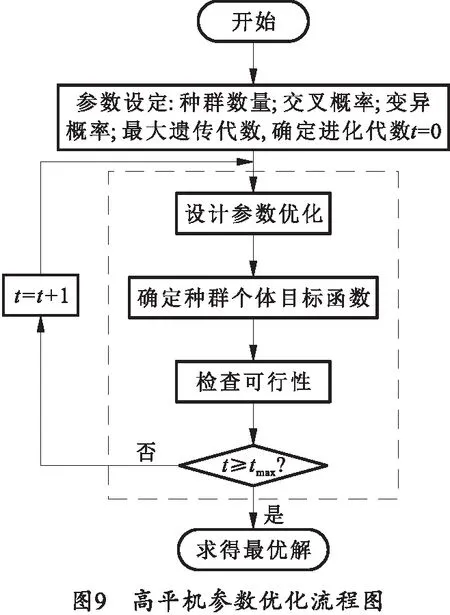
在火炮总体设计时,对各部件的分布位置有一个范围限制,考虑到某大口径火炮液体气压式高平机的布置位置和安装方式,笔者以一侧单个高平机为主要研究对象,选择前文分析的设计参数为主要优化设计参数,即高平机的前支点与耳轴点的距离R1,后支点与耳轴点的距离R2,活塞直径D,活塞杆直径D1及初始压强P作为设计变量。根据该型高平机的具体结构,考虑到零部件的实际加工情况和目标函数对各项设计变量的敏感度,以上设计参数的取值变化范围如表1所示。

表1 高平机优化设计参数表

选择衡量高平机平衡性能的主要指标,即高平机不平衡力矩,作为整个优化模型的最终的目标函数,并由高平机的具体结构形式确定该模型约束条件,则具体优化模型为

(9)

此处在利用遗传算法进行复杂系统参数优化时,其种群数量、交叉率、变异概率、迁移概率等参数的取值将对整体算法的收敛速度和全局最优解的正确性起着重要的影响作用。经过多次调整验算后,最终得出了本次高平机平衡性能优化模型中遗传算法的主要设定参数,如表2所示。

表2 遗传算法的参数选择

3.3 结果分析

根据上述高平机参数设定范围和遗传算法参数的取值,代入优化模型的主计算程序进行计算。这里需注意,由于活塞直径D及活塞杆直径D1在实际加工时,需取圆整数值,故此处对该部分优化后的结果参数进行合理圆整。优化后的高平机结构参数取值如表3所示。

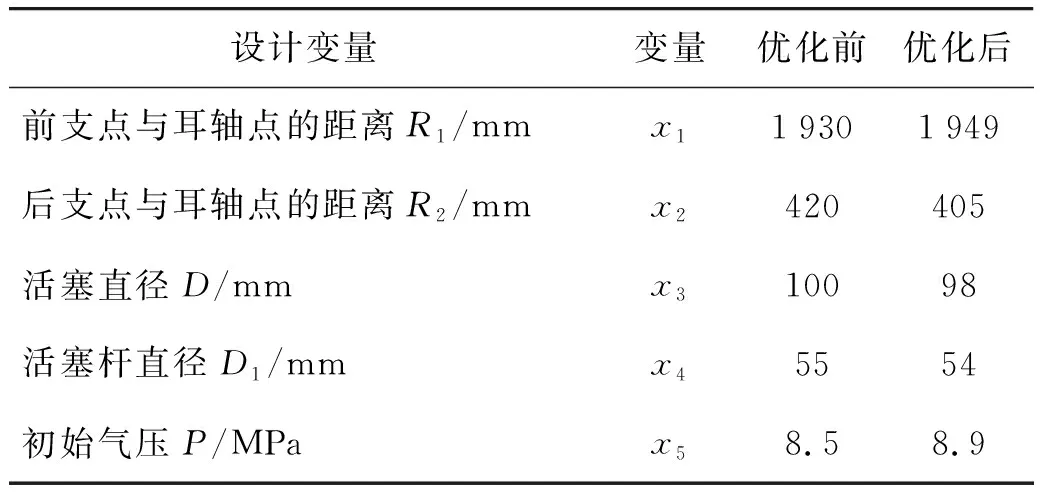
表3 高平机初始设计方案及优化方案

在保证满足高平机的设计约束条件下,高平机优化目标函数在常用射角0°～65°时的最大取值由3.568 kN·m降为2.850 kN·m,即优化后高平机的最大不平衡力矩下降约20.1%,在-3°～0°时的不平衡力矩最大值由-8.862 kN·m降为-7.350 kN·m,下降约17%,有效降低了高平机的不平衡力矩。高平机不平衡力矩在射角范围内的变化曲线如图10所示。

4 结论

笔者根据某大口径火炮液体气压式高平机的基本结构,建立了液体气压式高平机不平衡力矩计算模型,研究了高平机主要设计参数对其平衡性能的影响规律,并以某大口径火炮液体气压式高平机为例,引入遗传算法对平衡性能进行优化设计,得出主要结论如下:

1)高平机主要设计参数后支点与耳轴点的距离R2、活塞D及活塞杆直径D1、初始气体压力P对高平机工作中的平衡性能影响较大。合理调整高平机后支点与耳轴点的距离、活塞及活塞杆直径、初始气体压力可有效提高高平机的平衡性能。

2)优化分析结果表明,通过该设计优化方法,可将高平机不平衡力矩降低约20%,有效降低了火炮高低调炮时的不平衡力矩,提高了高平机的平衡性能,具有一定的优越性和工程应用价值。