用于不平衡冲量测试的一种六维力传感器结构设计

李凌志，刘志鹏，余文鑫，马凯华，郝郎迪

(1.南京理工大学 机械工程学院，江苏 南京 210094；2.吉林江机特种工业有限公司，吉林 吉林 132021)

动不平衡参数作为单兵无后坐炮最重要的安全性指标之一,其值会对武器射击精度和射击稳定性带来负面影响[1]。所以如何高效、精确地测量动不平衡参数,成为武器性能评估中不可或缺的一环。目前针对动不平衡参数的测试方法主要是导轨法和弹道摆法,以及其他各单位基于现有装置自行研发的测试系统。杨则尼等利用拉压力传感器设计了一种可直接测试炮轴方向上产生的不平衡力的实验装置,为导轨法测量动不平衡参数奠定了基础,同时提出这种测试方法存在的问题[2]。王志华等基于导轨法,通过设计固定架台部分装置,减少测试系统与发射装置因不同轴所产生的转矩[3]。庞春桥等通过自行设计的精密平衡测试装置,提出后后效期的影响过程,并结合相关理论提出一种轻型无后坐力炮动不平衡冲量现象的物理解释和有效评估方法[4]。

单兵武器发射过程中,发射器内的运动情况是十分剧烈以及复杂的。绝大多数测试系统只是针对所需参数进行点对点的测量,很少会在测量过程中对测试装置受到的空间力系进行实时监测。系统的不稳定性会对测量数据产生较大影响,导致与真实数据之间存在超出系统允许范围的误差。

六维力传感器作为工业智能化发展不可或缺的技术之一,是控制系统的重要组成部分。广义六维力传感器因其能够获取空间任意力系中的三维正交力及三维正交力矩,为后续各项性能指标的分析评估提供重要依据,在精密装配、航空机器人、汽车路测试验、火箭发动机推力试验和风洞试验等精度要求较高的场合发挥了极其重要的作用[5-7]。HAN通过软件集成各设计分析软件,对影响传感器灵敏度和刚度的13个结构参数进行同步优化,得到综合能力最优的尺寸参数,并验证传感器设计的合理性[8]。还有很多学者通过改进传感器弹性体结构,提高传感器灵敏度、刚度等性能,解决维间耦合、测量非线性载荷等问题,对其他多维力传感器的研发提供了参考[9-11]。

笔者基于十字梁式多维力传感器以及现有测试系统,设计了一种用于不平衡冲量测试的六维力传感器,使其在测试过程中,可实时监测系统所受各项力系。通过响应面法对弹性体尺寸参数进行优化,响应面模型选用Box-Behnken设计方法完成响应面试验设计,并通过有限元分析求解得到。结合有限元仿真对比分析和静态标定方法,证明优化过后的六维力传感器各项指标得到明显提高,达到测量需求,可用来指导下一步测试工作。

1 测试系统及六维力传感器数学模型

1.1 动不平衡冲量测试系统

笔者基于传统导轨法和现有测试系统,设计了一种利用拉压传感器测量动不平衡冲量的动不平衡测试系统,如图1所示。

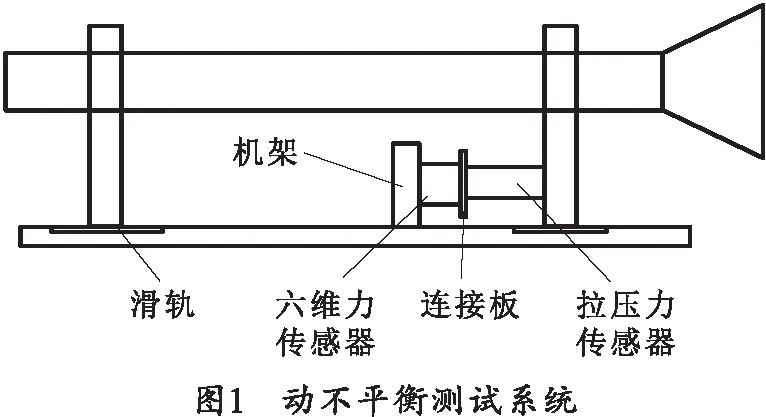
对影响单兵武器发射器动不平衡冲量的因素进行受力分析[12],笔者将六维力传感器安装在机架与拉压力传感器之间,通过连接板连接,Z轴方向与炮轴方向一致。六维力传感器各通道之间存在维间耦合的情况,在正常使用时都应经标定解耦后使用[13]。在动不平衡冲量测试中主要测量空间力系中三维正交力矩,经解耦得到对应数值,同时将解耦所测数据与拉压力传感器所测数据进行对比分析,所测数据可为无后坐炮的各项动不平衡参数的分析评估提供重要依据。

1.2 六维力传感器设计指标

结合相关数据及以往测试结果,用于不平衡冲量测试的六维力传感器主要设计指标如表1所示。

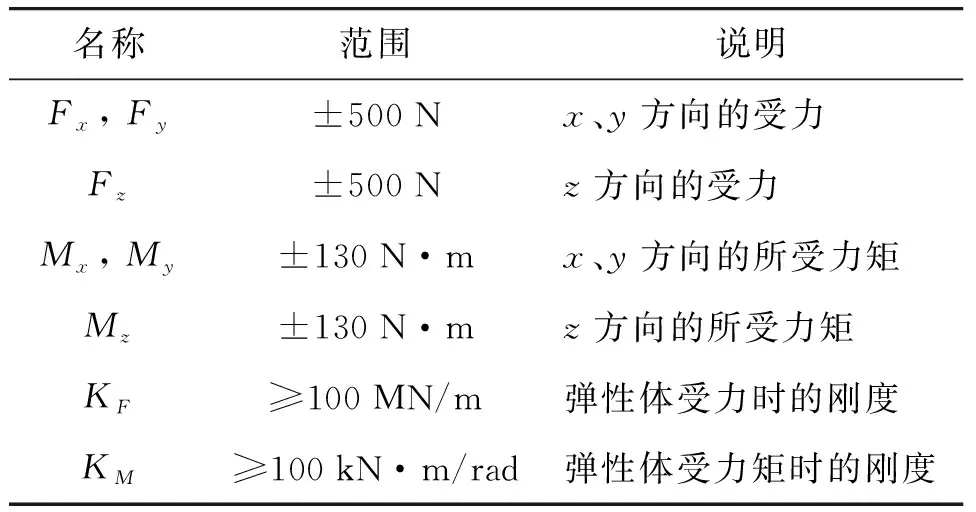
表1 六维力传感器设计指标

在进行不平衡冲量测试过程中,传感器实际输入范围F=±500 N,M=±130 N·m,考虑到传感器测量范围以及实际过载性能,在进行试验设计时,试验条件为Fx=Fz=1 500 N,Mx=Mz=200 N·m。

1.3 六维力传感器数学模型

笔者基于十字梁式六维力传感器,提出一种新型传感器弹性体结构,其由4个固定块、4个应变梁、4个转接块、8个浮动梁和1个加载块组成。通过在应变梁上开槽,令梁上应力集中于槽的两侧,提高传感器精度的同时保障后续应变粘贴工作的便捷性。综合考虑六维力传感器量程、刚度等因素,六维力传感器的材料选用马氏体沉淀硬化不锈钢0Cr17Ni4Cu4Nb,材料属性如表2所示。

表2 0Cr17Ni4Cu4Nb的材料属性

将设计完成的初始模型导入有限元软件进行静力学分析。在对模型施加边界条件时,将固定块上螺纹孔位置的节点位移完全约束,并在加载块螺纹孔处利用节点耦合MPC单元,随后单独施加各方向所对应的载荷。考虑到传感器弹性体结构和边界约束条件的对称性,在单独施加各方向载荷时,X和Y方向的计算结果一致,因此只考虑弹性体在受到Fx、Fz、Mx、Mz不同载荷的情况下,所得应变云图与变形情况,如图2所示。

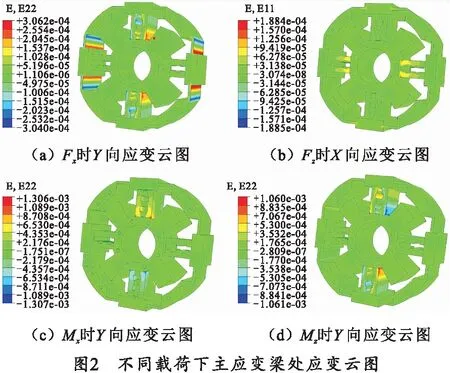
由图2可知弹性体受不同载荷时,应变集中区域都分布在应变梁开槽处,由此得到应变片粘贴位置,并采用全桥电路连接。确定初始弹性体模型,为后续响应面试验设计提供有限元结构分析基础。初始弹性体结构、应变片R1～R24粘贴位置及各测量通道使用应变片情况如图3所示。

2 响应面法试验设计

为使六维力传感器获得更好的测量性能,需要对弹性体的关键尺寸参数进行设计。由于弹性体结构复杂,尺寸参数较多,通过控制变量法对弹性体的各设计参数进行单因素模拟,选出对传感器性能影响较大的结构参数并确定其尺寸范围;采用响应面法,以尺寸参数及输出应变为变量对弹性体进行响应面试验设计,结合有限元仿真软件进行分析计算。采用多目标粒子群优化算法对模型进行优化求解。传感器的设计优化流程如图4所示。

2.1 传感器设计指标

2.1.1 灵敏度

对于应变式力传感器,通常定义传感器灵敏度为满量程下电桥输出电压与电桥输入电压的比值。电桥连接方式采用全桥连接。定义传感器灵敏度S为

(1)

式中:E0为测量电桥时的输入电压;UES为传感器满量程输出电压;Gf为应变片灵敏系数;ε1ES,ε2ES,ε3ES,ε4ES为每个应变片在满量程时对应的微应变。

对于六维力传感器而言,将灵敏度分为力测量灵敏度SF和力矩测量灵敏度SM,都是由力测量通道或者力矩测量通道中灵敏度最低的通道决定。假设两个通道灵敏度比值为SF/M,则

(2)

2.1.2 应变柔顺矩阵

应变柔顺矩阵往往用来描述六维力传感器其本身特性,和其尺寸参数无关。根据六维力传感器的工作原理,在量程范围内,电桥输出信号值与载荷值可近似认为线性关系,且维间耦合的形变量可叠加[14]。当Fx单独作用时,Fx测量通道输出量为u11,Fy测量通道输出量为u12,其余测量通道输出量以此类推;当Fy单独作用时,Fx测量通道输出量为u21,当Fz单独作用时,Fx测量通道输出量为u31,同理以此类推。根据输入与输出近似线性的假设可以得到:

(3)

式中,cij为表示输入与输出线性关系函数uij的斜率。

令作用在传感器上的载荷为Q,传感器在载荷Q=[Fx,Fy,Fz,Mx,My,Mz]T的作用下发生弹性变形时,应变柔顺矩阵可以表述为

(4)

式中,c11,c22,c33,c44,c55,c66分别为对应载荷下每个通道的灵敏度。

2.1.3 线性度和迟滞误差

理想条件下,传感器的输入与输出应该为线性关系,但实际上由于贴片工艺及制造工艺等因素,传感器实际测量过程中存在非线性误差。

定义传感器校准曲线与拟合直线间的最大偏差与满量程下输出的比值为线性度误差。同时定义传感器加载以及卸载过程中各输出点的最大差异值与满量程下输出的比值为迟滞误差。

线性度与迟滞误差是影响力传感器测量精度的关键因素之一。

2.2 单因素分析

以尺寸X3为例,结合控制变量法及有限元软件进行计算,以传感器性能为决定因素。经过多次实验筛选,选择对应变柔顺矩阵影响较大的弹性体尺寸变量,如图5所示。图中,X1为浮动梁厚度,X2为应变梁厚度,X3为应变梁高度,X4为转换块厚度,X5为转接块高度,单位均为mm。

2.3 响应面试验设计

为了得到最优模型。利用响应面设计软件,选择Box-Behnken设计方法,基于弹性体的结构参数完成响应面试验设计一共46组,结合仿真得到响应值y1,y2,y3,y4,响应为施加载荷时所对应的测量通道的应变值,试验条件为Fx=Fz=1 500 N,Mx=Mz=200 N·m。由材料力学可知,微应变没有单位,本文中用με表示,即1με=1×10-6。最后通过最小二乘法对所得数据进行拟合得到响应面模型。

2.4 多目标优化的约束条件和优化目标

已知响应面模型yi(x),采用多目标粒子群优化算法(Multi-objective Particle Swarm Optimization, MOPSO)对其进行优化。设置初始种群个数为40,空间维数为5,最大迭代次数为120。

根据测量要求,力矩通道测量灵敏度的优先级应大于力通道测量灵敏度,假设函数

f(x)=0.4f(y3)+0.3f(y4)+0.2f(y1)+0.1f(y2).

(5)

传感器弹性体在不同载荷Q=[Fx,Fy,Fz,Mx,My,Mz]T的作用下应具有足够的刚度K:

(6)

传感器两个测量通道灵敏度平衡,两个通道测量灵敏度的比值SF/M尽量小,SF/M越小,力和力矩测量灵敏度越接近。

六维力传感器的优化问题可以用如下数学问题表达:

求设计变量x=[x1,x2,L,x6]T,

(7)

2.5 标定实验

对响应面模型进行多目标优化得到最优模型,与初始模型进行对比分析。确定传感器最优尺寸大小并加工得到六维力传感器原理样机。

根据已有设备设计一种六维力传感器静态标定装置,对原理样机进行静态标定实验,求解出标定方程:

Q=C-1(U-B),

(8)

式中:矩阵U为传感器输出电压矩阵;B为常量。笔者已提前将数据进行归零处理,这里B=0。

六维力传感器及标定系统如图6所示。

3 结果与分析

3.1 单因素仿真试验结果

由于控制变量法分析过程较为单一,笔者以应变梁的高度为例,研究应变梁高度X3在载荷Fx、Fz、Mx、Mz下对传感器的性能影响,如图7所示。图中,定义per为影响程度,以百分数形式表示,E为应变,S为应力,U为位移/转角。从图7中可以很直观地看出,X3的大小直接影响传感器的性能,最大提升57%,最小降低49%。同理,通过分析其他尺寸对弹性体性能影响,得到设计尺寸范围,试验因素与水平如表3所示。

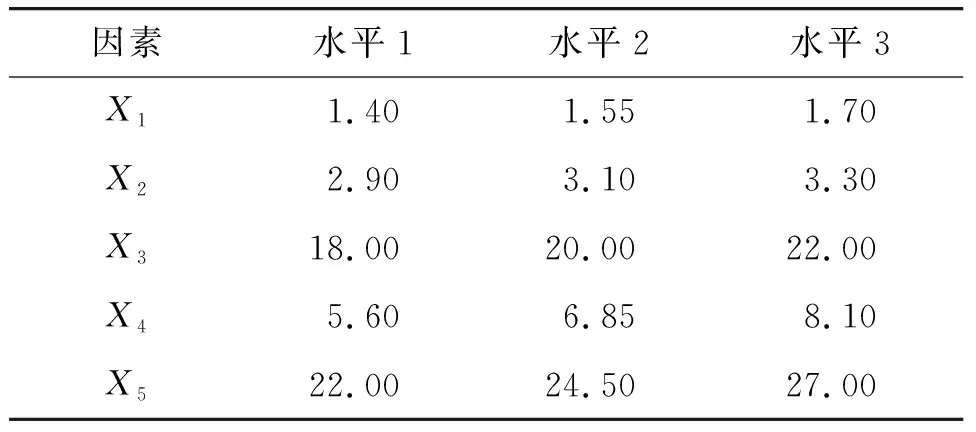
表3 六维力传感器主要设计目标

3.2 响应面模型及优化结果

由于文章篇幅有限,仅给出响应面试验设计部分结果数据,如表4所示。

表4 响应面试验分析表

结合响应面设计软件,采用最小二乘法对上述响应面试验设计结果数据进行拟合,得出传感器弹性体在不同载荷作用下的响应面模型yi(x):

(9)

(10)

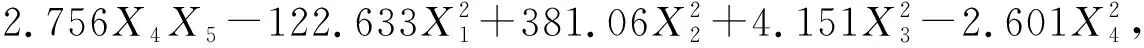
(11)

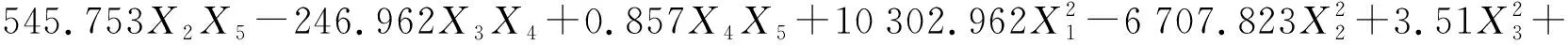
(12)

对响应面模型y1(x)～y4(x)进行统计学分析,结果如表5所示。

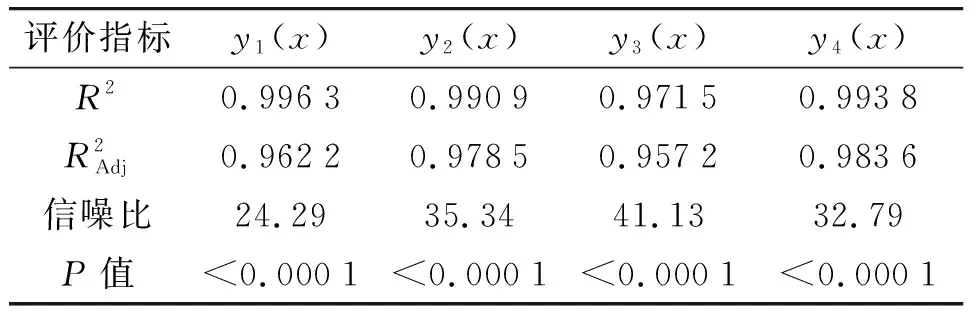
表5 响应面模型的相关系数及方差分析

对每个响应面模型进行方差分析,可知每个模型的P值均小于0.000 1,表明该响应面模型显著,这意味着模型可以用来指导下一步的设计。

根据约束条件和优化目标得到弹性体最优尺寸参数,与初始设计时的参数对比如表6所示,性能参数对比如表7所示。由表7可知,优化模型每个测量通道的响应值相比初始模型均大幅增加,其中Mx测量方向的响应值最高提升了31.02%,Mz方向测量方向的响应值提升了21.24%,符合传感器测量需求。

表6 弹性体尺寸参数对比 mm

表7 弹性体性能对比

3.3 静态标定

对原理样机进行力/力矩加载试验,设计一种静态标定装置对传感器进行静态标定,所有测量通道输出均为对应电压(U/mV),标定结果如图8所示,并计算得到传感器标定方程,如式(13)所示。

(13)

根据传感器标定方程计算得到六维力传感器各通道灵敏度(mV/V)与维间干扰如表8所示。可知,加工得到的六维力传感器力测量灵敏度为0.30mV/V,力矩测量灵敏度为1.22mV/V。经静态解耦后各通道之间耦合误差最大为1.01%。

表8 六维力传感器灵敏度与耦合误差

根据计算得知六维力传感器各维度的线性度及迟滞误差,如表9所示。可知,该传感器的线性度均小于2%,最大的线性度是Fz方向,为1.60%,最大的迟滞误差是Fz方向,为1.03%。

表9 六维力传感器线性度与迟滞误差 %

与有限元分析结果相比,通过标定得到的六维力传感器各项静态性能指标,力测量通道灵敏度较低,力矩测量通道维间耦合较高。造成这种现象的原因有如下几点:零件加工误差、贴片工艺限制和标定过程中力加载方向等方面。

六维力传感器通过静态标定后,各项性能指标达到测量需求。

4 结束语

笔者以改进单兵武器动不平衡冲量测试系统为目标,针对测试系统工作状态时的受力情况,设计了一种可实时监测正交力系的六维力传感器。通过单因素分析和响应面法试验设计,结合有限元分析得到响应面模型,基于多目标粒子群优化算法得到最优结构尺寸参数,并搭建六维力传感器静态标定系统。

优化结果表明力矩通道响应数值最大提升32.24%,力通道响应数值最大提升31.02%。标定结果表明传感器力测量灵敏度为0.30 mV/V,力矩测量灵敏度为1.22 mV/V,解耦后各通道维间耦合误差最大为1.01%,线性度和迟滞误差均小于2%。

设计并研发的六维力传感器具有良好的测量性能,满足实际测量需求。研究结果可为多维力传感器在单兵武器动不平衡测试系统中的应用提供参考。