钨合金破片侵彻钢靶的穿靶能量研究
洪豆, 郑宇, 李文彬, 李一鸣, 姜宁
(南京理工大学 智能弹药技术国防重点学科试验室,江苏 南京 210094)
几十年来,如何对目标进行侵彻毁伤一直都是国内外研究的热点,有如穿甲弹之类的整体式弹丸侵彻,也有如射流和破片之类的毁伤元侵彻。其中,钨合金作为一种高强度,高密度的材料,以预制破片的形式被广泛应用于杀爆战斗部中。因此,对钨合金破片侵彻能力的研究具有重要的应用价值[1-2]。
一直以来,研究破片穿透靶板的能力主要是通过理论和仿真的方法研究破片的极限穿透速度和极限穿甲深度,并用破片极限速度来表征破片的穿靶特性。张庆明[3]用能量法建立了破片极限穿透速度的理论分析模型,运用可靠性理论确定了极限速度的试验方法。黄长强[4]运用量纲分析与多元线性回归结合的方法,建立了球形破片极限穿透速度公式,提高了计算精度。徐豫新[5]通过研究破片穿甲后的破损情况,得到了破片直径与极限穿深的关系。Cheng[6]通过研究表明,在数值模拟中,使用Johnson/Cook塑性损伤模型研究破片在中低速冲击下侵彻靶板具有较为有效。Kalameh[7]提出用光滑粒子流体力学(smooth particle hydrodynamics,SPH)方法模拟研究破片高速撞击金属靶板的过程,较好地描述了弹丸的侵彻和开坑。
随着科研学者对破片穿靶效应的探索和研究,破片极限穿透速度公式逐渐被完善,其适用范围越来越广,计算精度也越来越高。但是,由于在相同弹靶条件下,破片初速越高,穿透靶板所需要的能量也越大[8]。单用破片极限穿透速度表征破片的穿靶特性仍具有一定的局限性。本文通过研究钨合金球形预制破片对钢板的侵彻效应,使用量纲分析的方法,得到了破片穿靶能量与破片速度的关系式。用14.5 mm弹道枪发射不同直径的钨球进行穿甲试验,并将试验结果与计算值进行了对比。
1 破片侵彻数值模拟
1.1 仿真模型
运用AUTODYN数值仿真软件研究钨合金球形破片的速度对穿靶能量的影响,选用mm-mg-ms的单位制,利用8 mm直径的球形破片作为侵彻体,靶板厚度为6 mm。为得到高精度的仿真结果,2种模型都选用拉格朗日网格建模,且单元均使用拉格朗日算法,接触设定为侵蚀接触,其侵蚀应变为200%。靶板最小尺寸为0.5 mm,建模时采用1/2模型,如图1所示。
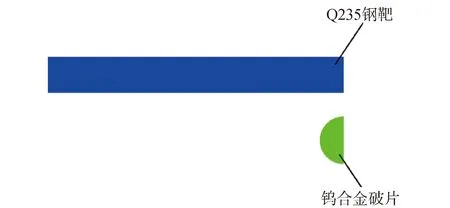
图1 球形破片1/2仿真模型Fig.1 1/2 simulation model of spherical fragment
破片材料选用钨合金,密度为17.5 g/cm3,靶板材料选用Q235钢,密度为7.83 g/cm3,2种模型均采用Johnson-Cook本构方程和Shock状态方程,根据文献[9-13]得到材料参数如表1所示。

表1 钨球与钢板的材料基本特性Table 1 State equation parameters of tungsten ball and steel plate
1.2 结果分析
数值仿真计算中,破片速度由低到高,从500 m/s开始慢慢增加,直至700 m/s。图2为球形破片在不同速度下侵彻钢板的仿真结果。

图2 钨球侵彻靶板开坑图Fig.2 Pit drawing of tungsten ball penetrating target plate
通过测量仿真结果中破片侵彻钢板的开坑直径,绘制如图3开坑直径随破片速度的变化曲线。从图3中可以看出,靶板的开坑直径会随着破片速度的增大而增大。这是由于破片在侵彻钢板时,球形破片在高速碰撞下受到强烈的压缩,使得破片与靶板的接触面积增大,从而导致开坑直径的增大。
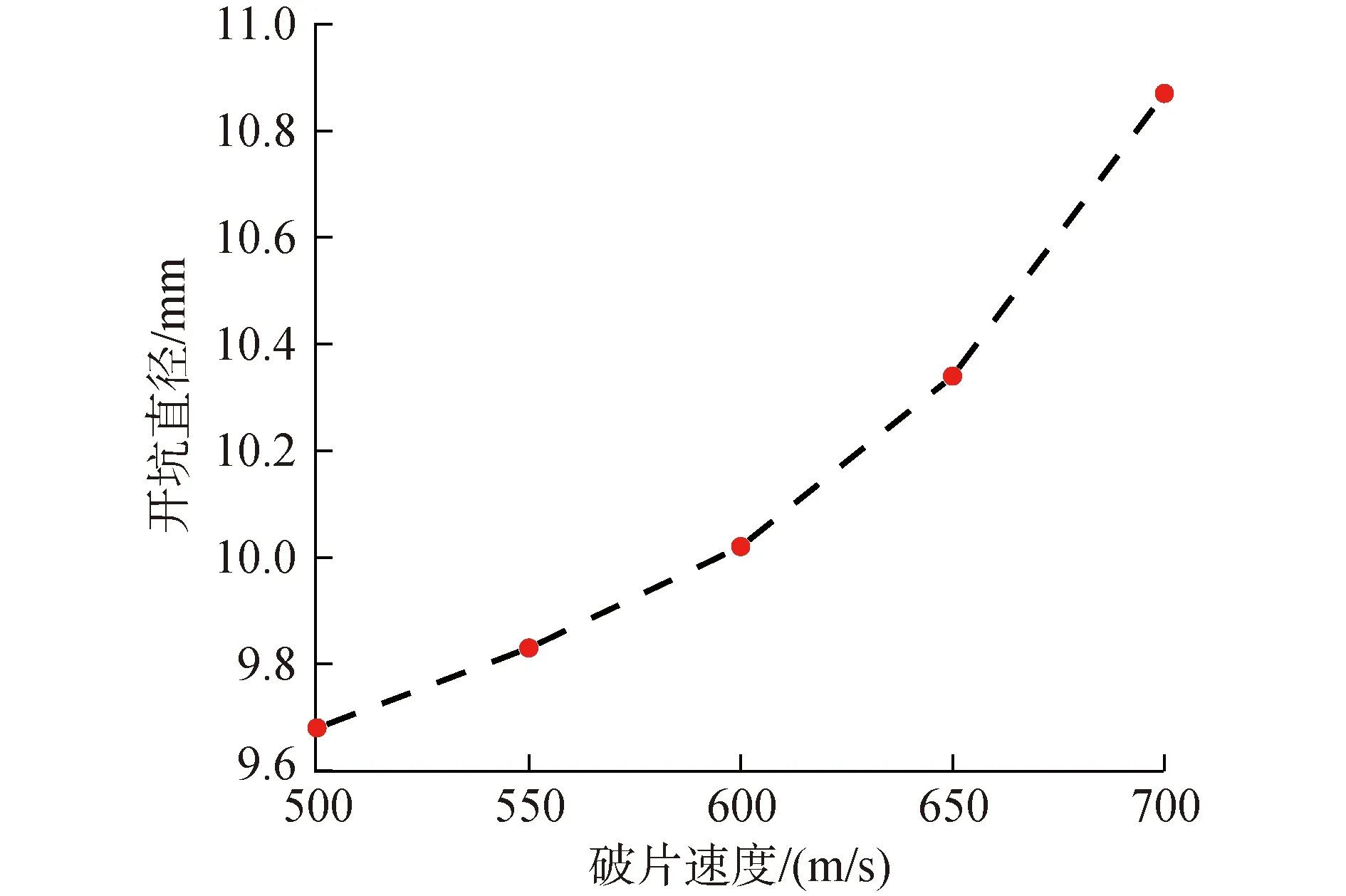
图3 开坑直径与破片速度关系曲线Fig.3 Relation curve between pit diameter and fragment velocity
文献[4]极限穿透经验公式中,弹靶接触面积也作为极限穿透速度的影响因素:
(1)
式中:k为试验符合系数;h为靶板厚度,m;d为球形破片直径,m;S为破片着靶面积,m2;ρt为靶板材料密度,kg/m3;ρf为靶板材料密度,kg/m3;σt为靶板强度极限,Pa。
破片着靶面积越大,破片的极限穿透速度越大。而破片极限穿透速度也可表示成破片在极限状态下穿靶能量,所以破片速度对破片穿靶能量有一定影响。
通过数值仿真得到破片速度与破片穿靶能量的关系,如图4所示。破片穿靶能量会随着破片速度的增大而增大,且在低速阶段,两者具有明显的线性关系。当破片速度提高40%时,破片穿靶能量也相应地提高了24.9%。
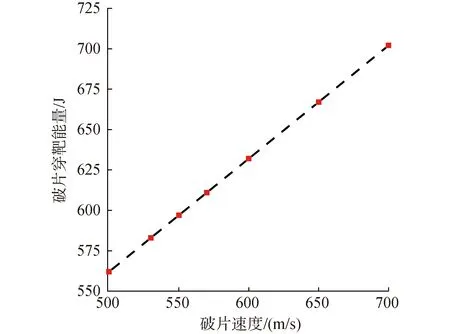
图4 破片速度与穿靶能量关系曲线Fig.4 Relation curve between fragment velocity and target penetrating energy
从上述对仿真数据分析中可以看出,破片初速对穿靶能量有较大的影响,单纯以极限穿透速度来描述破片穿靶能量过于片面。在研究多层靶或破片对靶后效应物的毁伤时,破片初速大于极限穿透速度,使用极限穿透速度计算,会造成较大的误差。因此,需要建立相应的穿靶能量公式。
2 破片穿靶能量公式
破片对靶板的侵彻过程是一个复杂的过程,建立一个能够准确计算穿靶能量的理论公式较为困难。因此,本文在量纲分析的基础上,建立一个统一的穿靶能量公式。
为了便于穿靶能量公式的建立,现对撞击过程做如下简化:1)忽略侵彻过程中的一切热效应;2)将破片视为刚体,不计其变形;3)侵彻过程中,破片沿直线飞行。
基于黄长强极限穿透速度公式[4]的形式,通过量纲分析法,建立破片穿靶能量公式。球形破片侵彻靶板过程所涉及的主要因素及其在公式单位下的量纲如表2所示。根据给定的上述参数,破片穿靶能量函数式为:

表2 主要因素及量纲Table 2 Main factors and dimensions
E=f(h,d,ρf,ρt,v0,σt)
(2)
式(2)中含有4个独立量纲,可提取d、v0、ρf、σt作为基本量,各量值所满足的关系式为:
(3)
函数f展开可得:
(4)
对式(4)进行调整可得:
(5)
从式(5)中可以看出,在一定的弹靶条件下,破片穿靶所需能量与破片初速成正比,这与图4中所表示的线性关系吻合。
把穿透能量用入靶速度和出靶速度替换,可得:

(6)
等式两边进行化简可得:
(7)
式中A、B是随弹靶系统变化而改变的变量,当弹靶系统确定时,A、B为常量。
对仿真的数据用式(7)进行拟合,得到图5。

图5 入靶速度与出靶速度曲线图Fig.5 Curve of target velocity and residual velocity
从图5可以看出,式(7)能很好地拟合出入靶速度与出靶速度的关系曲线图,即所推导出的穿靶能量公式在形式上具有一定的可行性。
当破片速度为极限穿透速度时,即
v0=vlim
(8)
(9)
结合式(5)、式(8)和式(9)可得:
(10)
式中x、y值需要通过试验进行标定。
式(10)为极限穿透速度的计算式,故破片穿靶能量函数式也可通过改变形式成为极限穿透速度公式。
3 穿靶能量试验
3.1 试验方案
采用直径为7 mm和8 mm的钨合金球体作为侵彻元,靶板采用6 mm厚的Q235钢,进行球形预制破片穿甲试验,确定x、y的值。其中,Q235钢的屈服强度为235 MPa,密度为7.83 g/cm3;钨合金的密度为17.8 g/cm3。
试验装置及其布置如图6所示,它包括14.5 mm弹道枪、防护板、靶板、弹托和高速摄影机等。把钨合金破片放入弹托中,以保证发射时为密封状态,并通过调整发射药量来控制破片初速的大小。破片飞离枪口后,与弹托分离,并穿过防护板的洞口打向靶板。弹托被防护板拦截。破片速度测试方法是在试验前通过标杆标定破片弹道方向的距离,试验中通过高速摄影机捕捉破片在运动过程,将破片前后2帧破片运动的距离与帧数的乘积,即为破片速度。
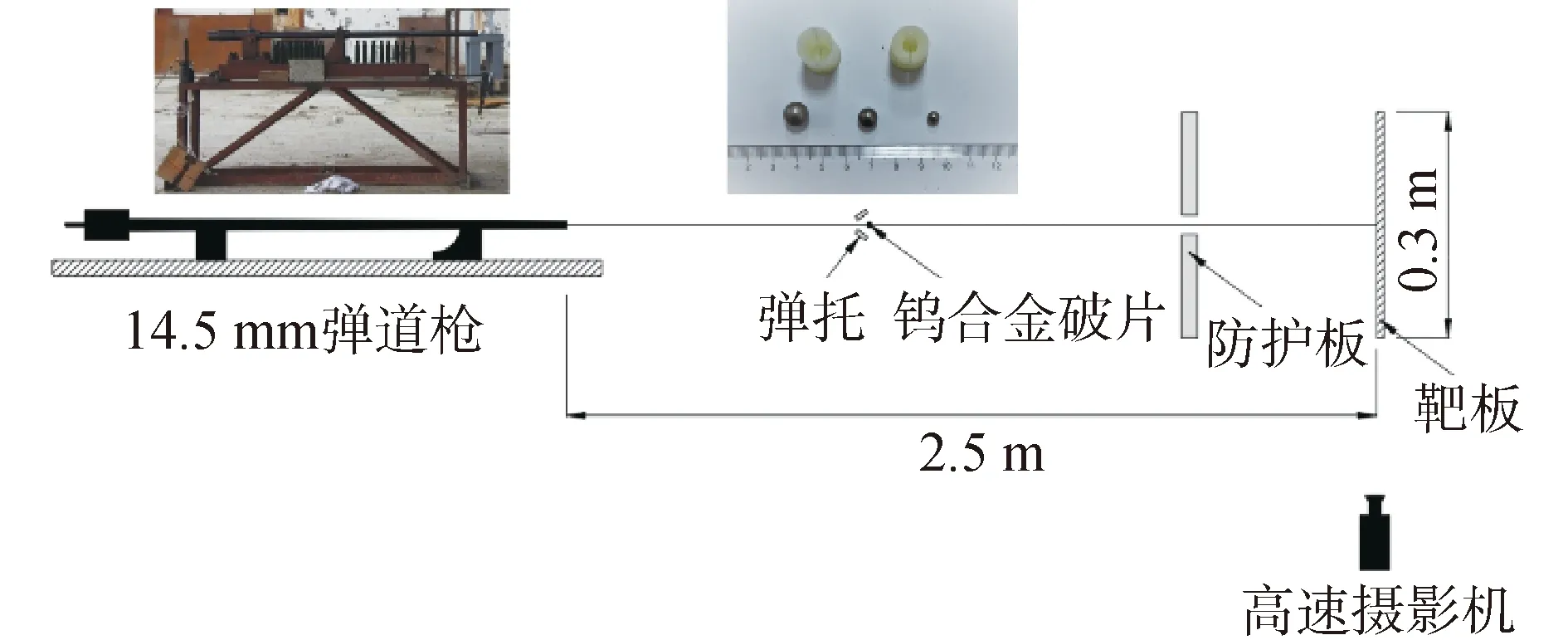
图6 试验装置布置示意Fig.6 Layout of test device
3.2 试验结果分析
穿过6 mm靶板共进行了8次试验,其中2次试验使用7 mm钨球,6次试验使用8 mm钨球,试验结果如表3。
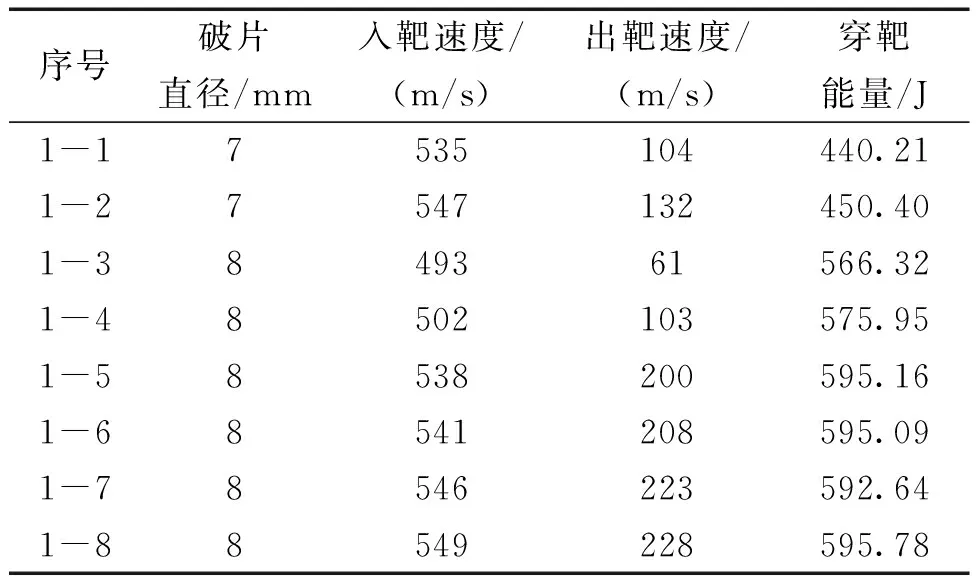
表3 7、8 mm钨合金球形破片穿靶试验Table 3 Penetration test of 7 mm and 8 mm Tungsten alloy spherical fragments
通过表4对比8 mm钨合金球形破片侵彻6 mm Q235钢靶的试验值与仿真值可知,试验与仿真的误差均在5%以内,由此可知仿真具有一定的的可信性。
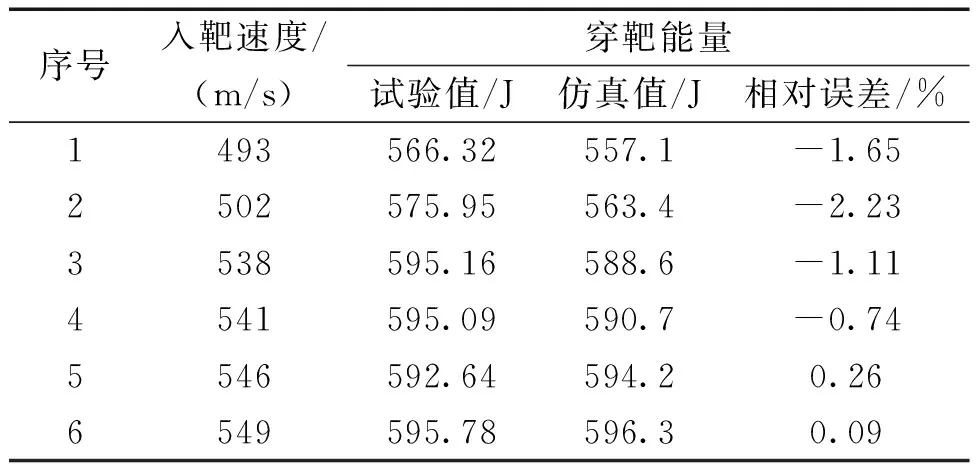
表4 8 mm破片侵彻6 mm钢板穿靶试验与仿真对比Table 4 Penetration test of 7 mm and 8 mm Tungsten alloy spherical fragments
设7 mm钨合金破片穿靶所需能量为E1,8 mm钨合金破片穿靶所需能量为E2,则:
(11)
(12)
联立式(11)和式(12),可得:
(13)
(14)
将表3中的试验数据代入式(13)和式(14)中,可以得到12组x、y的数据,如表5所示。x与y的平均值分别为1.478 9和-0.663 8。由表5数据可知,当破片为钨合金,靶板为钢靶时,x值约为1.478 9,y值约为-0.663 8,代入式(5)中可得:
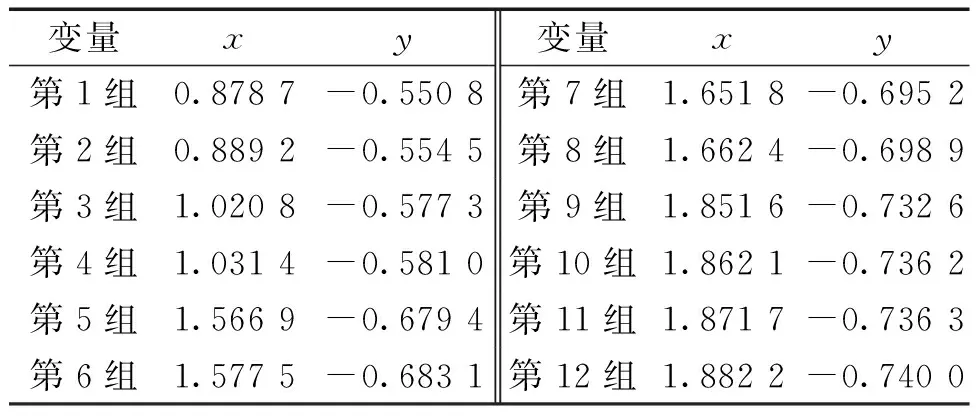
表5 x、y数据标定值Table 5 x、 y data calibration values
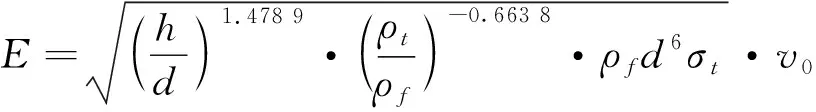
(15)
破片穿靶能量公式修正后,试验值、式(15)穿靶能量计算值和极限穿靶能量计算值随速度变化趋势如图7所示。当破片速度接近极限穿透速度时,极限穿靶能量计算值与试验值之间的相对误差要小于穿靶能量计算值与试验值的相对误差。随着破片速度的增大,极限穿靶能量计算值与试验值的相对误差持续增大,而穿靶能量计算值与试验值在随速度变化时具有相同的变化趋势,误差始终保持在5%以内。
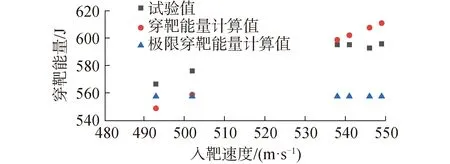
图7 8 mm破片穿靶能量随入靶速度的变化Fig.7 The change of energy of 8 mm fragment penetrating target with target entering velocity
由上述对极限穿靶能量与穿靶能量计算值的比较结果可知,使用穿靶能量公式能较好地描述破片侵彻靶板的结果。
3.3 验证试验
为验证钨合金球形破片侵彻钢板的穿靶能量公式的准确性,使用3种分别为4.8、9.5和10 mm的钨球对厚度6 mm的Q235钢靶进行穿甲试验,采用高速摄影机对破片进行测速,试验数据见表6。
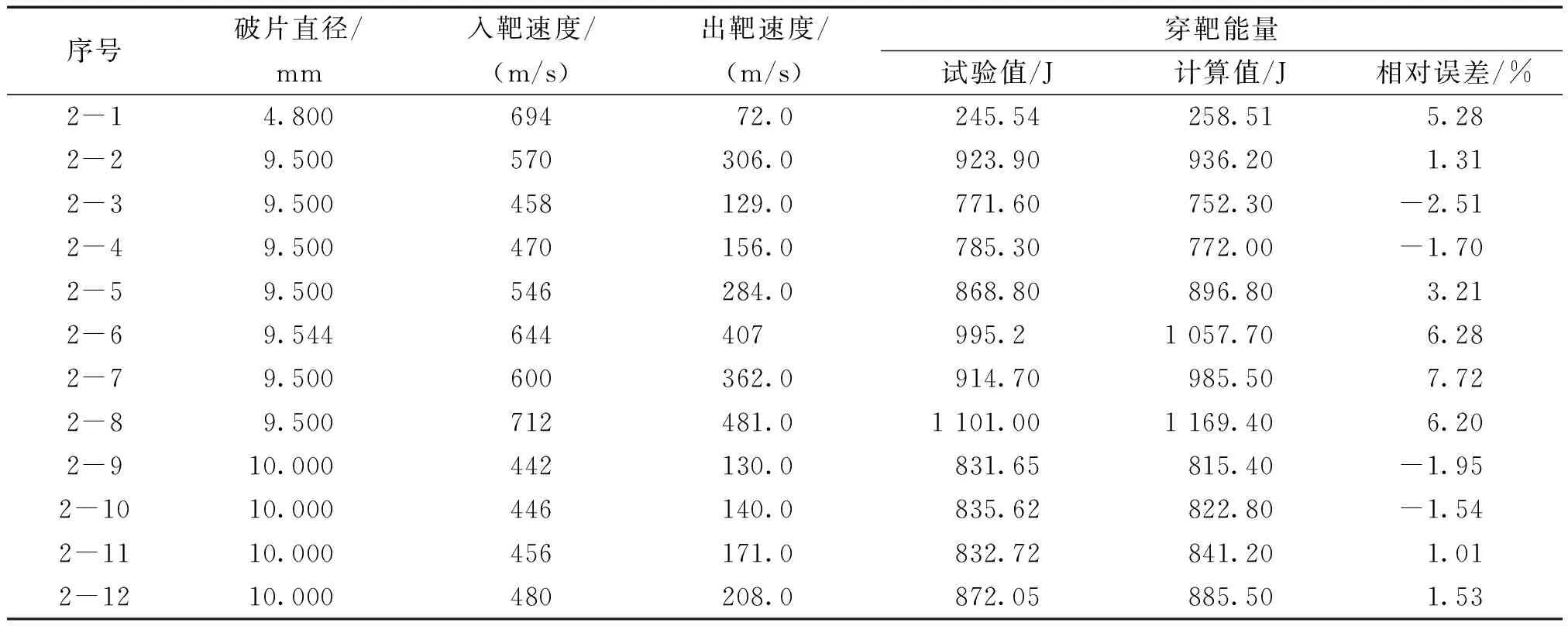
表6 多种钨合金球形破片穿靶试验Table 6 Penetration test of various tungsten alloy spherical fragments
从表6中的试验统计结果中可以看出,穿靶能量公式的计算值的最大误差不超过7.72%,平均误差在3.35%左右。因此穿靶能量公式的计算值能满足工程需求,具有一定的应用价值。
为进一步分析不同弹靶系统下入靶速度与穿靶能量间的关系,绘制不同直径钨球侵彻靶板的入靶速度与穿靶能量关系曲线以及入靶能量与穿靶能量关系曲线,可得图8。
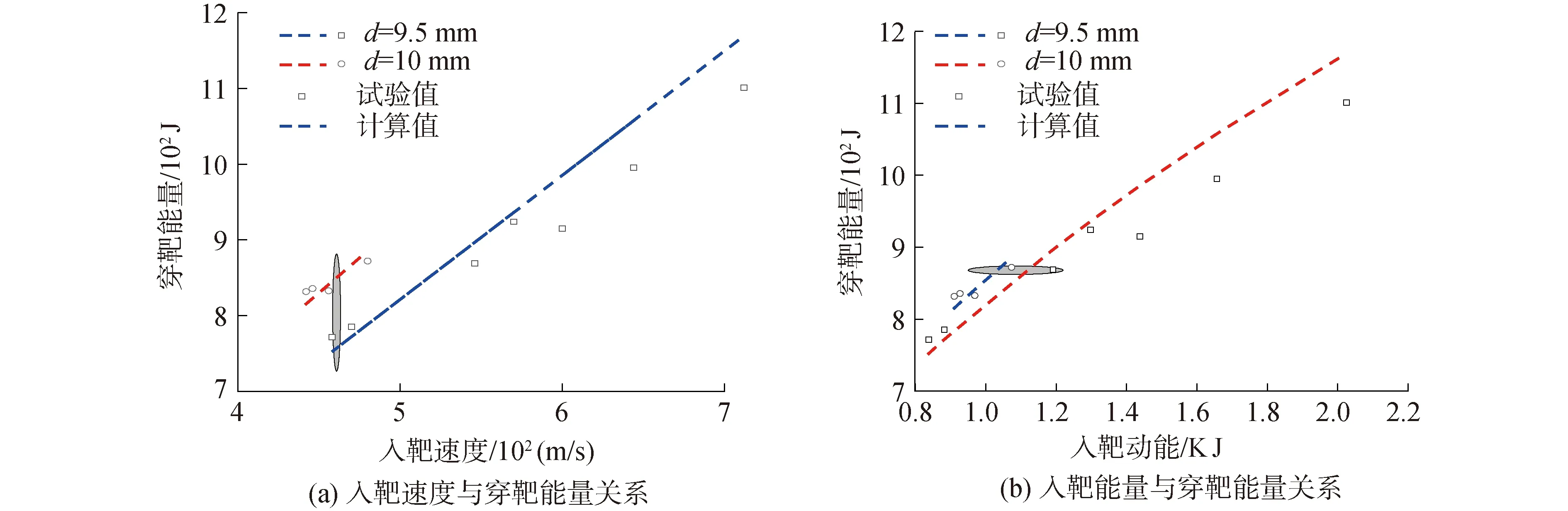
图8 穿靶能量随入靶速度和能量变化规律Fig.8 The variation of target penetration energy with target entering velocity and energy
从图8(a)中可以看出,不同直径的钨球侵彻靶板,其穿靶能量都将随着穿靶速度的增大而增大。从灰色的椭圆区域中可以看出,在相同速度下,钨球的直径越大,侵彻靶板的穿靶能量越大。
从图8(b)的灰色区域中可以看出,在相同穿靶能量下,直径为9.5 mm破片的入靶动能大于直径为10 mm破片的入靶动能。因此在破片穿靶时,直径越大的破片,所需的入靶动能反而越小。
4 结论
1)通过量纲分析理论得到了钨合金球形破片侵彻钢板的穿靶能量计算公式,且利用该公式得到的计算值与试验值吻合较好,误差在10%以内,满足工程需求。
2)在同一弹靶系统下,破片完全侵彻靶板时,破片入靶速度越高,靶板开坑直径越大,破片穿靶所需能量也越高,且在低速阶段,穿靶能量与入靶速度具有明显的线性关系。
3)当不同尺寸的破片在相同速度下完全侵彻靶板时,破片直径越大,破片所需穿靶能量也越大;不同尺寸的破片在相同侵彻靶板的穿靶能量下,破片直径越大,破片所需的入靶动能越小。

