基于层次分析与BP神经网络的电梯安全评价模型
乔维德
(无锡开放大学 科研与发展规划处,江苏 无锡 214011)
随着我国电梯行业高速发展和电梯产量的不断增长,电梯安全事故时有发生,严重影响了人们正常的工作生活[1]。长期以来,为减少电梯故障率,通常采取定期检修方式对电梯加以维护。当电梯检修不及时而处于危险状态时,不仅会影响电梯的正常运行,还可能会产生事故导致财产损失及人身伤亡。因此,对电梯进行安全运行评估,科学准确地把握电梯安全状态,及时发现并主动消除电梯存在的安全隐患,对于保障电梯安全可靠运行具有十分重要的现实意义。
许多学者及工程技术人员对电梯安全状态评估进行了大量的分析研究。文献[2-3]采用层次分析原理对电梯进行安全评估;崔增林[4]提出基于灰色关联分析法和层次分析法的电梯安全评价方法,在一定程度上消除或减少了电梯的安全隐患;陈兆芳等[5]提出基于熵权和灰色关联方法的电梯安全评价方法,构建影响电梯安全运行的人、机、环境、管理4个方面10个因素的评价指标体系,基本实现电梯整体安全水平等级的评价;陶杰等[6]提出一种综合层次分析法、熵权法、模糊综合评价法的电梯安全运行状态评估模型,有助于人们掌握电梯安全状态,具有一定的工程实用性;文献[7-8]提出利用反向传播(back propagation,BP)神经网络建立电梯安全综合评价方法;万舟等[9]将层次分析法与粒子群算法优化BP神经网络的方法运用于电梯安全状态评价,实现了电梯安全评价的智能化。
以上评价方法虽然取得了一定的成效,但仍然不够完善,存在明显的不足,主要表现在:电梯安全评价研究一般只涉及安全评价指标体系的构建,而各评价指标之间的权重系数分配很少涉及,具体评价时也没有结合具体案例进行实证分析。由于电梯是一种复杂的机电设备,具有较强的非线性、时滞性和不确定性,如果单一采取层次分析法、熵权法等传统评价方法,往往不能客观准确地评价电梯的安全状态及其性能,因此基于神经网络的电梯安全评价不失为一种比较有效的方法。但现有评价中的神经网络所采取的BP算法存在收敛速度慢、计算时间长、搜索效率低等缺点,粒子群算法也容易出现“早熟”现象,而且在完全搜索前容易陷入局部极值,极大地影响电梯安全评价速度及准确率。
为快速、准确地对电梯运行状态及其性能进行安全评价,本文以在用电梯为研究对象,在全面分析电梯安全影响因素基础上,利用层次分析法构建电梯安全状态评价指标体系,建立基于改进粒子群优化BP神经网络的电梯安全评价模型,为在用电梯的安全评估与及时检修提供必要的理论指导。
1 电梯安全评价指标体系构建
1.1 评价指标体系建立
利用层次分析法建立电梯安全评价指标体系时,应以系统工程思维分析问题,以客观性、科学性、目的性以及效益性为基本原则,注重评价指标的共性与个性、定性与定量的有机结合与有效转化。评价时不仅考虑在用电梯系统的各个组成部分,还要重点分析影响电梯安全稳定运行的重点环节和关键因素,以及影响电梯安全运行各因素之间的关联度。
由于影响电梯安全运行的外界环境及内在因素多而复杂,所以对在用电梯进行安全评价时,要考虑电梯设备本身的安全运行情况、影响电梯使用的环境因素、电梯的使用管理情况与维护保养情况,以及相关人员因素等。基于上述分析,在咨询相关技术人员与专家,并参考相关文献的基础上,建立在用电梯安全运行状态评价的三层结构模型,如表1所示。

表1 电梯安全运行评价指标体系Table 1 Evaluation index system of elevator safety operation
1.2 指标体系中指标权重确定
由表1可知,在用电梯安全运行状态评价的三层结构模型由目标层A、一级指标层U、二级指标层X组成,其中二级指标层包含27个指标因素。为了确定各指标权重,利用1~9比率标度法综合分析电梯评价指标体系中各指标的重要程度(数值越大,关系程度越大),然后在反复征询电梯行业安全技术专家、电梯生产厂家及电梯用户意见基础上,得出电梯安全评价的一级指标权重判断矩阵A,二级指标权重判断矩阵U1、U2、U3、U4、U5,分别如表2~表7所示。
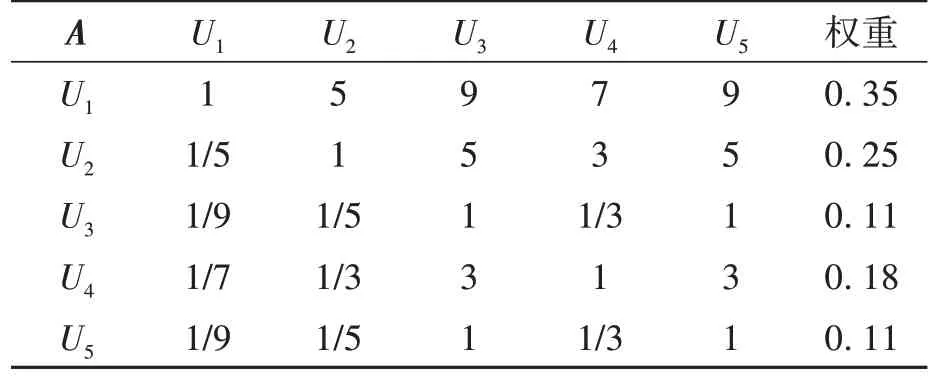
表2 一级指标权重判断矩阵ATable 2 First-class index weight judgment matrix A

表3 二级指标权重判断矩阵U1Table 3 Secondary index weight judgment matrix U1

表4 二级指标权重判断矩阵U2Table 4 Secondary index weight judgment matrix U2
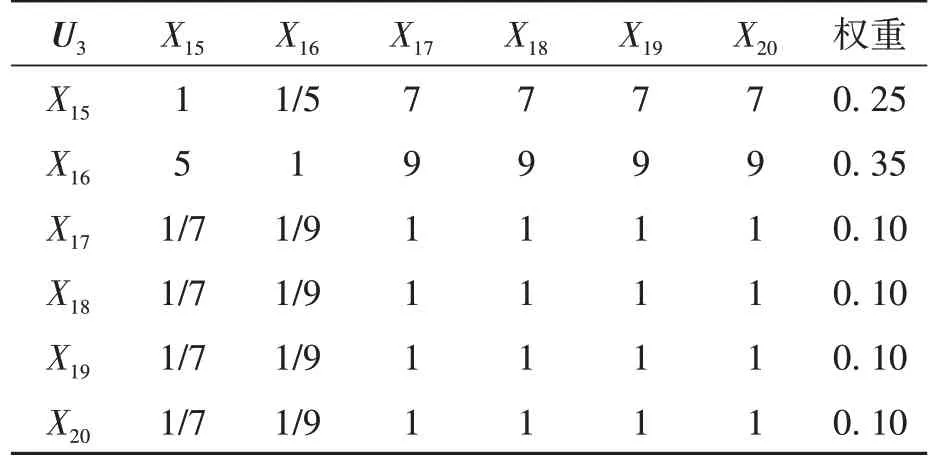
表5 二级指标权重判断矩阵U3Table 5 Secondary index weight judgment matrix U3

表6 二级指标权重判断矩阵U4Table 6 Secondary index weight judgment matrix U4
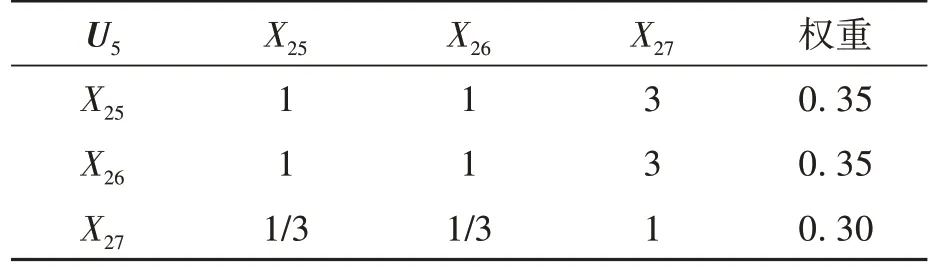
表7 二级指标权重判断矩阵U5Table 7 Secondary index weight judgment matrix U5
通过对指标权重判断矩阵测算,将一级指标层中的电梯设备、使用环境、使用管理、维护保养和相关人员情况所占权重分别设定为0.35、0.25、0.11、0.18、0.11,其他指标权重判断矩阵依此类推。在求得各指标判断矩阵的特征向量并进行归一化处理后,得到电梯安全状态评价的二级评价指标X1~X27相对于目标层的合成权重,如表8所示。
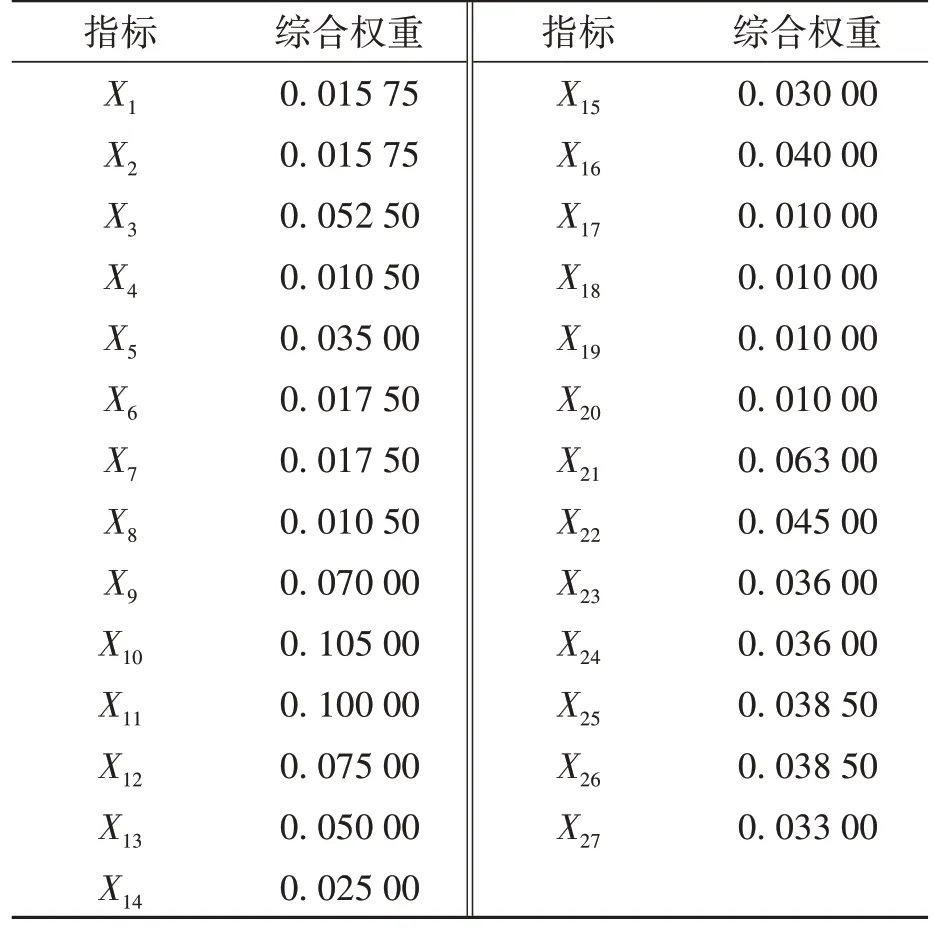
表8 电梯安全评价指标合成权重Table 8 Synthetic weight of elevator safety evaluation index
2 电梯安全评价模型
运用BP神经网络建立的在用电梯安全评价模型如图1所示。通过改进粒子群算法优化BP神经网络初始结构参数;选取训练样本,采用改进BP算法对BP神经网络加以训练;最后利用测试样本对训练好的BP神经网络进行测试验证。
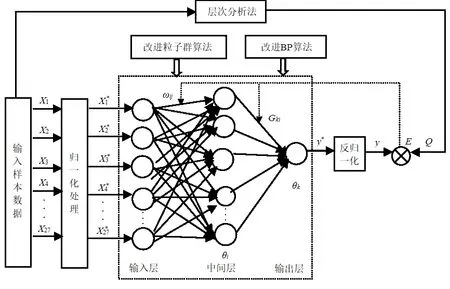
图1 电梯安全评价模型Fig.1 Elevator safety evaluation model
训练和测试样本选自电梯安全评价体系中27个指标所对应的数据样本,其中训练样本一般选取样本总数的70%~90%,测试样本选取样本总数的10%~30%。BP神经网络输入为经过归一化处理的指标数据x1*~x27*,输出为y*;y*经过反归一化处理得到在用电梯网络安全评价值y,y与BP神经网络设定的期望值Q(通过上述层次分析法计算得到的综合评价得分)之间的差值为E;误差信号E沿原来连接通路反向传播,并不断修正网络连接权值ωij、Gki,直至E满足规定精度要求。图1中ωij、Gki分别为网络输入层与中间层、中间层与输出层神经元之间的连接权值(i=1,2,…,P1,P1为输入层神经元节点的个数;j=1,2,…,P2,P2为中间层神经元节点的个数;k=1,2,…,P3,P3为输出层神经元节点的个数);θi和θk分别为中间层、输出层神经元的阈值。
3 BP神经网络的优化及训练
3.1 粒子群算法的改进
标准粒子群算法根据公式(1)、(2)迭代寻优,直至求出粒子最优位置Gb(t)。
式中:a=1,2,…,N,N为粒子群中粒子的数量;b=1,2,…,M,M为求解空间的维数;t为当前迭代次数,次;vab(t)为t代时粒子的速度,m/s;Sab(t)为t代时粒子的位置,m;Pab(t)为第a个粒子在t代时所经历的个体最优位置,m;Gb(t)为群体所有粒子所经历的最优位置,m;ω为保持粒子运动的惯性权重;γ1、γ2为加速因子,分别用来调整个体和全局最优粒子位置方向的最大移动步长,一般取γ1=γ2=2;c1、c2为[0,1]的随机数。
标准粒子群算法容易出现早熟[10],需要对惯性权重按式(3)进行动态调节。
式中:ωmax、ωmin分别为惯性权重的最大值、最小值;tmax为最大迭代次数,次。
为增加粒子群算法寻优空间,降低或避免陷入局部极值,借鉴遗传算法中种群变异机理,在粒子每次更新迭代后引入遗传变异因子。在迭代初期为发挥粒子群算法自身特点,采用较小变异率;随着迭代次数增多,算法的多样性变差,采用较大的变异率,以扩大搜索最优粒子的位置范围,避免算法陷入局部最优,保证粒子群算法的全局最优化。
改进后的粒子位置计算公式如式(4)所示,粒子变异率公式如式(5)所示。
式中:Smax为粒子最大位置,m;h表示[0,1]间的随机值,决定着粒子朝着最大或最小位置方向的变异;gt为变异率;g1、g2分别为变异率的初值和终值,这里取g2>g1,使得变异率按余弦规律从小逐渐变大。
3.2 BP算法的改进
标准BP算法在网络学习中极易陷入局部极小,从而产生振荡乃至发散现象。为此,可通过加入动量项和自适应学习因子的方法进行改进[11],具体如式(6)、式(7)所示。
式中:β为动量因子;|ωij(t)-ωij(t-1)|为动量项;d、f为常数,且0<d<f;η为变化中的学习率,即步长;σ为网络层之间的误差;Xi为BP神经网络的输入数据。
3.3 神经网络优化及训练
BP神经网络的优化训练流程框图如图2所示,主要步骤如下:
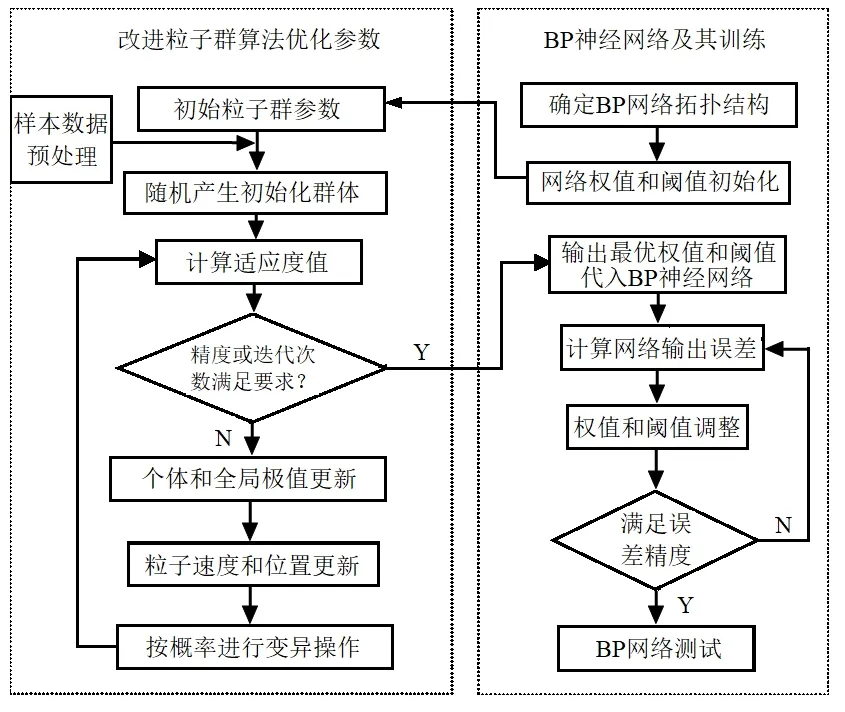
图2 BP神经网络优化训练流程示意图Fig. 2 Schematic diagram of BP neural network optimization training process
(1)初始化粒子群参数、确定神经网络拓扑结构。随机设定粒子群的初始位置、初始速度、初始惯性权重、加速因子、迭代最大次数,以及动量因子、学习率等。假设BP神经网络拓扑结构为P1—P2—P3,种群个体粒子对应网络层所有神经元连接权值和阈值,粒子维度为P1×P2+P2×P3+P2+P3,连接权值个数为P1×P2+P2×P3,阈值个数为P2+P3。
(2)选取在用电梯安全评价的训练及测试样本,在进行归一化处理后,采用网络输出误差E作为粒子适应度值,即
式中:Qlk为第l个训练样本在网络第k个输出节点的期望输出;ylk为第l个训练样本在网络第k个输出节点的实际输出;n为训练样本数。
(3)求得的粒子适应度值如果高于全局最佳位置的粒子适应度值,则该粒子位置为当前全局最佳位置。
(4)利用式(1)~式(3)更新粒子速度和位置,再按式(4)、式(5)进行变异操作。
(5)返回步骤(2),直至粒子适应度值满足精度要求或达到最大迭代次数时,结束粒子群算法,并输出粒子全局最佳位置,即输出对应神经网络最优的初始连接权值ωij、Gki及阈值θi、θk。
(6)按式(6)、式(7)采取改进BP算法训练BP神经网络,不断修正网络连接权值和阈值,直至网络输出规定的误差精度。
(7)将归一化后的测试样本输入已训练完毕的BP网络,对电梯安全评价网络模型进行测试验证。
4 在用电梯安全评价模型应用
4.1 样本数据处理
选取无锡市锡山区、梁溪区、新吴区3大城区6个小区共80部正在使用的住宅电梯,按照上述评价体系进行安全综合评价。采样时,对于电梯安全评价指标体系中的定性指标,先请电梯行业技术专家按百分制打分,转换为定量指标数据,从而得到样本数据如表9所示(表中X1~X27为BP神经网络输入对应的电梯安全评价指标值,Q为电梯安全专家评价结果)。
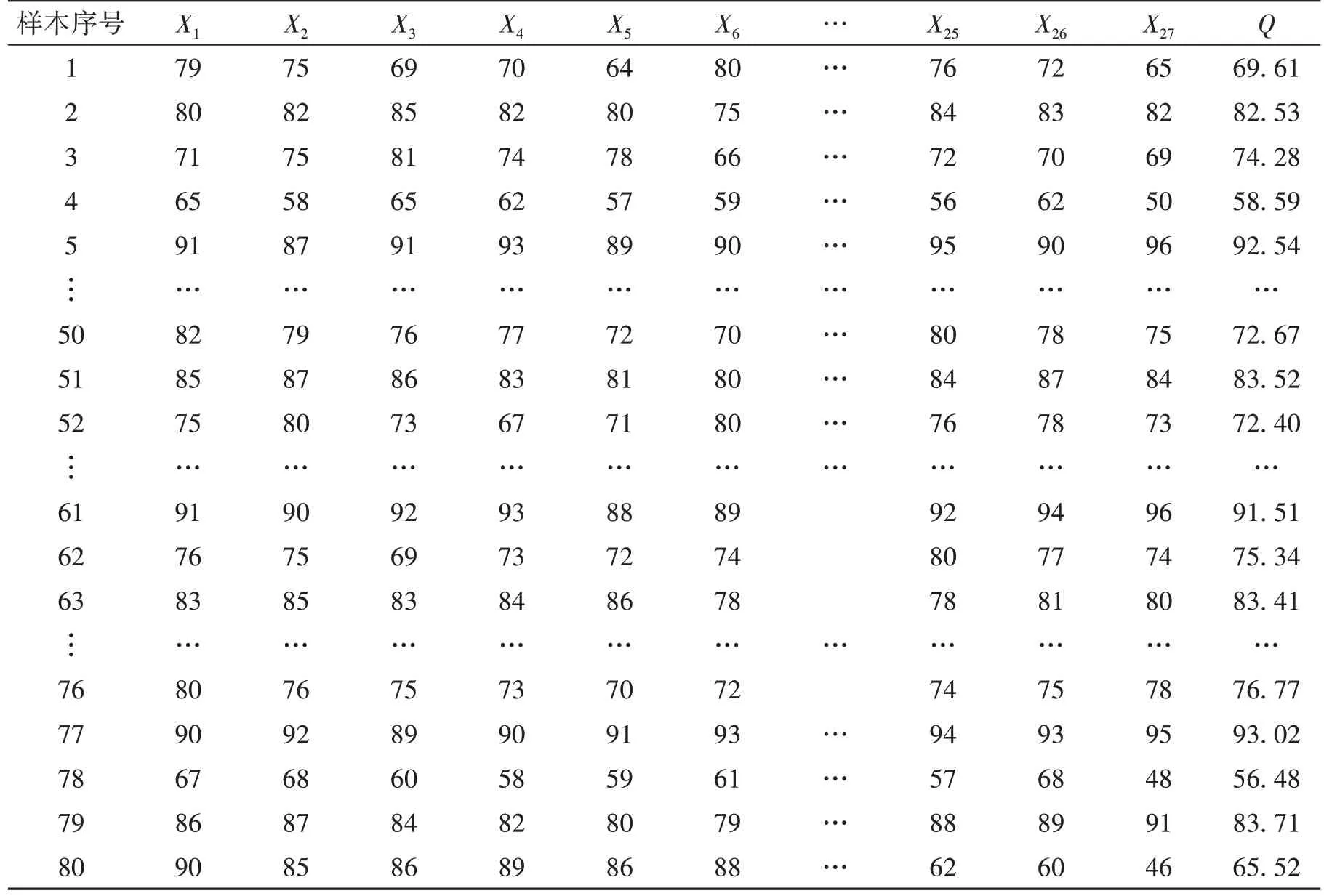
表9 在用电梯安全评价数据样本Table 9 Elevator safety evaluation data sample in use
考虑输入样本数据对BP神经网络训练速度、训练精度的影响,利用MATLAB工具箱中的mapminmax函数功能对输入样本数据进行归一化转换,保证样本数值处于[0,1],从而得到均匀化、平滑性分布的数据[12]。
输入数据归一化处理公式如下:
式中:X*为归一化后的数据;X、Xmax、Xmin分别为网络输入的原始样本数据及其最大、最小值。
神经网络输出后采取反归一化处理,使之恢复为正常的电梯安全评价值。反归一化处理公式如下:
式中:y为网络输出的反归一化值;y*、ymax、ymin分别为网络输出及其最大、最小值。
4.2 神经网络拓扑结构确定
由于在用电梯安全评价体系有27个指标,取BP神经网络输入层神经元数量P1为27、输出层节点数P3为1,中间层神经元节点个数P2由经验公式P2=[(2P1+P3)1/2,2P1+P3]确定。经过反复计算测试,确定P2为30,因而BP神经网络拓扑结构为27—30—1。
4.3 网络训练及测试
将表9中的80组在用电梯样本分为训练样本和测试样本,其中1~70号为训练样本,61~80号为测试样本,即61~70号样本同时用于交叉训练和测试。设定BP神经网络训练误差精度为10-4,并根据表8电梯安全评价指标合成权重和表9的样本数据,得到各样本的综合得分,如表9所示,再以此数据作为BP神经网络的期望输出Q。
利用MATLAB工具软件,对BP神经网络采取改进粒子群算法,再用表9中的70组训练样本进行仿真训练,然后用20组测试样本对训练完毕的网络加以检验,得到BP神经网络评价模型输出结果如表10所示(表中评价等级是根据评分值确定的,共分5个等级,分别为评分值为[90,100]时等级为好、评分值为[80,90)时等级为较好、评分值为[60,80)时等级为一般、评分值为[45,60)时等级为较差、评分值为[0,45)时等级为差)。
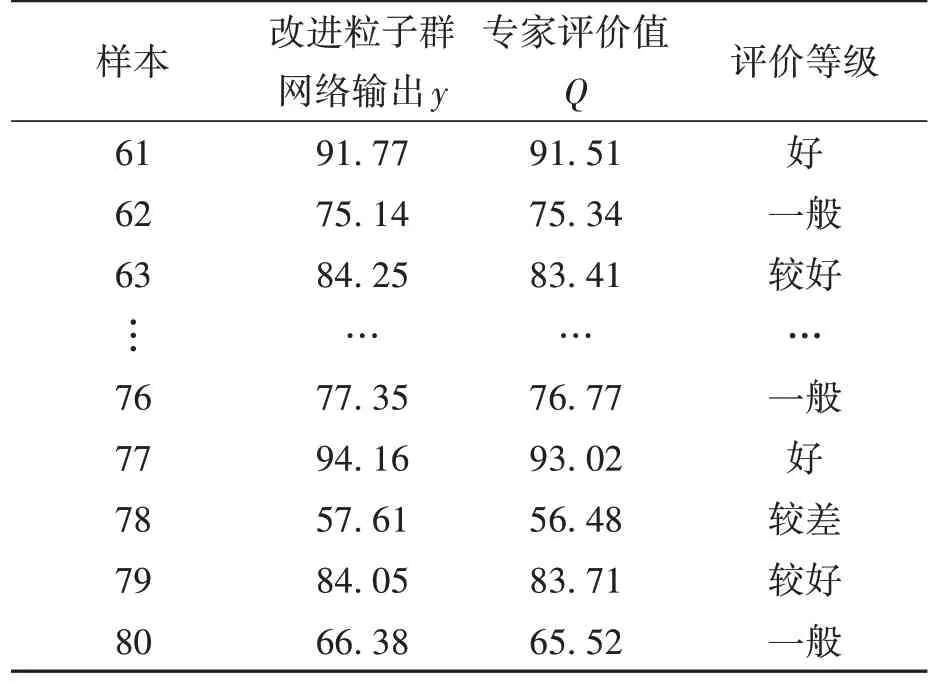
表10 BP网络评价与专家评价值比较Table 10 Comparison of values between BP network evaluation and expert evaluation
为便于与层次分析法得到的专家评价结果比较,将表9中专家评价结果也列于表10,并将神经网络评价模型与专家评价结果的误差绘成曲线,如图3所示。
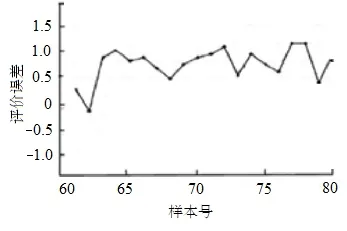
图3 电梯安全神经网络评价与专家评价误差Fig.3 Error of elevator safety between neural network evaluation and expert evaluation
由表10可知,20组测试样本的神经网络输出与专家评价结论完全相同;由图3可知,20组测试样本的神经网络输出与专家评价值之间的最大绝对误差不超过1.25。因此,BP神经网络评价模型可用于在用电梯的安全评价,且评价准确性高。
4.4 几种算法的仿真结果比较
为验证改进优化的BP神经网络模型在电梯安全评价中的优势,将1~70号训练样本输入BP神经网络,分别采取已有文献中的BP算法、粒子群算法训练BP神经网络[13],再将表9中的20组测试样本输入训练后的神经网络,得到各算法的性能指标如表11所示。
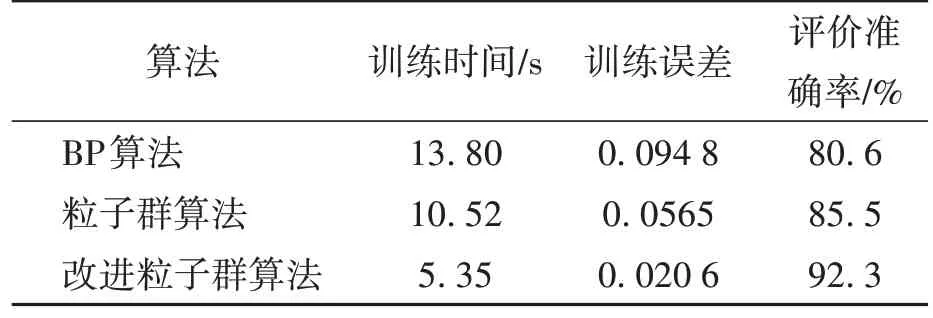
表11 几种算法性能比较Table 11 Performance comparison of different algorithms
为便于比较,将经本文改进粒子群算法对表9中20组样本(61~80号)测试后的结果也列于表11。由表11中可知,经过改进粒子群算法优化的BP神经网络训练速度最快,训练时间为5.35 s,分别比BP算法的13.80 s、粒子群算法10.52 s快8.45 s、5.17 s;训练误差最小,为0.0206;评价准确度最高,达92.3%,分别比BP算法的80.6%、粒子群算法的85.5%提高了11.7%、6.8%。显然,改进粒子群算法优化的BP神经网络模型是一种很有效的在用电梯安全状态评价方法。
5 结语
通过层次分析法建立在用电梯安全运行评价指标体系,运用BP神经网络建立电梯安全评价模型。仿真结果表明,经过改进粒子群算法优化的BP神经网络比其他算法训练速度最快、训练误差最小、评价准确度最高。显然,改进粒子群算法优化的BP神经网络模型是一种很有效的在用电梯安全状态评价方法,对于保障在用电梯的安全可靠运行具有较大的工程应用价值。

