一种复杂地形下智能移动机器人路径规划与控制研究

刘飞

关键词：复杂地形；移动机器人；自抗扰控制；随机生成树

0 引言

复杂地形下智能移动机器人研究非常重要，这一研究领域已经成了机器人技术的热点之一[1-2]。随着科技的不断发展，越来越多的工作被机器人所代替[3]。在很多场景中，特别是在工业生产、军事作战、海洋勘探、医疗卫生等领域，机器人已经发挥了重要作用，而智能移动机器人则是其中的重要一环[4]。因此，相关的理论研究需要进一步提升[5-8]。在复杂地形下，智能移动机器人需要具备一定的智能和自主学习能力，能够通过感知和决策，完成任务并避免意外事故的发生[9]。同时，智能移动机器人还需要具备一定的适应性，能够应对不同的环境和任务需求[10]。因此，智能移动机器人的研究需要综合运用规划与运筹、机器学习、控制理论等多学科知识，不断提升机器人的智能和自主性[11]。在工业生产中，智能移动机器人可以实现物流自动化、装配自动化、巡检自动化等多种功能，提高制造效率和质量[12]。在军事作战中，智能移动机器人可以用于情报侦察、无人侦察、战场救援等多个方面，提高作战效率和安全性[13]。在海洋勘探中，智能移动机器人可以用于深海勘探、海洋环境监测等领域，提高勘探效率和减少人员风险[14]。在医疗卫生领域，智能移动机器人可以用于手术辅助、康复训练、护理等方面，提高医療水平和服务质量[15]。但在实际应用中，智能移动机器人还需要考虑到安全性、可靠性、可操作性等多种因素。综合以上应用场景，智能移动机器人的研究不仅仅是理论探讨，更需要实际应用与验证。只有在实际应用中不断优化和完善，才能真正实现机器人技术的突破和发展[16-20]。总之，复杂地形下智能移动机器人研究非常重要，会在很多领域带来巨大的工程价值。随着技术的不断进步和应用的不断拓展，智能移动机器人的研究和发展将会成为机器人领域的重要发展方向之一。

1 移动机器人运动规划

针对移动机器人执行复杂地形下运动的特殊性，需要考虑到复杂地形的特殊性，才能够真正地规划出一条从任务起点到终点的最优或次优路径[14]。通过对常见复杂地形的分析与抽象，设定以下的规划约束条件。具体包括三个重要条件：

1） 机器人移动时应遵循最优路线，包括路径最短及运动时间最少；

2） 机器人所处的复杂地形存在障碍物，且地面不平整存在起伏现象；

3） 机器人与障碍物之间存在安全距离。

综上，以上因素都是路径规划算法需要考虑到的约束条件。经分析后需要考虑以下具体内容。

1.1 空间坐标系定义

移动机器人在复杂地形中运动时，因为不仅存在起伏地形，能够抽象为凹型及凸型地面。常规的位置及姿态描述一般只考虑OX、OY 及偏航角。但本文研究的机器人在复杂地形，特别是存在起伏地形，所以将常规的位姿描述拓展为六自由度模型，包括表示位置的三个向量和表示姿态的三个向量。

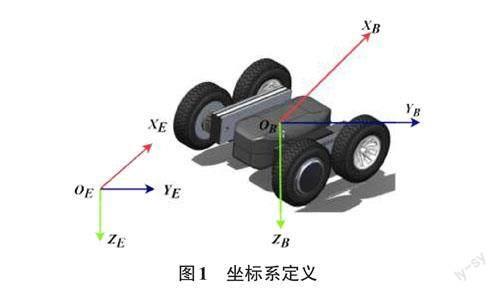
首先建立坐标系，包括大地坐标系OE XEYE ZE 和机体坐标系OB XBYB ZB，坐标系的定义满足右手定则，如图1所示。其中，大地坐标系原点OE 绑定于地球质心，OE XE 指向正北方向，OEYE 指向正西方向，OE ZE 指向地球质心；移动机器人几何中心与质心重合，并且作为机体坐标系的原点OB，OB XB 指向机器人前进方向。通过欧拉角形式表示移动机器人的姿态，定义如下：绕OB XB 轴旋转的角度定义为滚转角φ，绕OBYB 轴旋转的角度为俯仰角θ，绕OB ZB 轴旋转的角度为偏航角ψ。

1.2 安全运动距离

移动机器人的路径规划问题是解决机器人在空间中最佳运动路径的优化问题，需要设计出一个能够快速有效处理搜索算法，能够高效求解出最优的空间运动路径，同时确保机器人能与障碍物间保持最小安全运动距离，如图2 所示。假设在大地坐标系OE XEYE ZE 中，pi 表示为移动机器人在复杂地形下的位置向量；obj是运动空间下的障碍物；d 是机器人与障碍物间的安全运动距离。则机器人在空间中的位置pi、障碍物obj、距离d满足以下条件，如式（1） 所示。

Dis（ pi，obj ） ≥ d （1）

其中，Dis（ pi，obj ） 表示机器人在空间中的位置pi到障碍物obj之间的距离。

1.3 机身尺寸

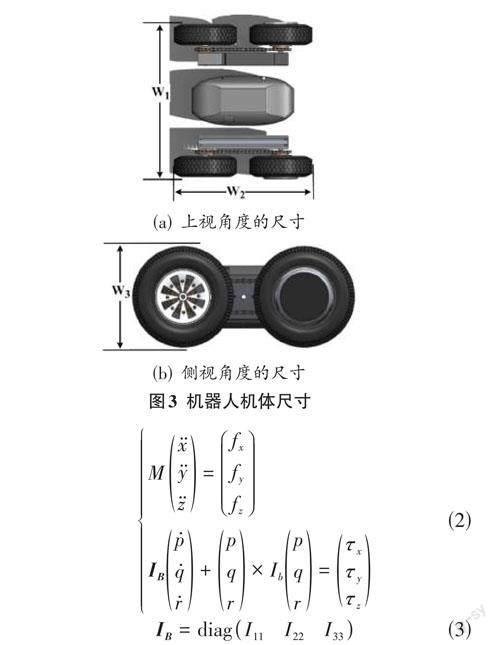
在复杂地形存在地面不平整、狭小通道等状态，需要将机器人的自身尺寸作为路径规划的先验条件。如图3所示，表示移动机器人的尺寸。W1、W2表示上视角度下的尺寸，W3表示侧视角度下的尺寸。

2 移动机器人控制算法设计

2.1 动力学建模

定义好复杂环境下的坐标系之后，同时综合考虑机身尺寸。根据机器人学有关理论及工程实现的目标，通过牛顿-欧拉方法建立该机器人的动力学模型。有关的位置和姿态由向量形式予以表示。其中，位置向量为（x，y，z ），姿态向量为（?，θ，ψ），采用欧拉角形式，单位为度（°，degree） 。同时定义机体坐标系下的角速度向量为（ p，q，r ），所以根据牛顿-欧拉方法建立的动力学模型有：

其中，fi 是动力系统作用于整个移动机器人上的总驱动力。总驱动力在机体坐标系OB XBYB ZB 分解为三维分量，τi 是总驱动力矩在机体坐标系上的三维分量。M 是移动机器人的质量，IB是转动惯量矩阵。

2.2 控制器设计

为实现移动机器人适应复杂地形环境中的运动，需要机器人的控制器具备自适应能力，同时也要对环境干扰具备一定的抗扰能力。本文研究是在高压强电磁环境中使用，环境复杂且干扰因素多，很难得到精确模型，因此选择使用采用无模型的自抗扰控制方法（Active Disturbance Rejection Control，ADRC） 。同时考虑到需要对环境具有自适应能力，因此选择BP神经网络对ADRC进行参数自适应改进。

在无模型控制方法中，ADRC是与工程应用广泛的，且能够有效抵抗环境干扰的一类方法[15]。国内学者韩京清于1995年提出，通过期望输入与反馈输出间的误差作为控制器输入信号，再通过算法模块输出控制量消除误差。主要算法模块是三个：跟踪微分器（TD） 、扩张状态观测器（ESO） 和状态误差反馈率（SEF） 。这三个模块互相配合后，能够获得很好的控制效果[16–18]。图4是ADRC的典型结构。

移动机器人控制器的设计方法需要考虑到复杂地形下不同因素造成的多类型扰动，比如风的力学作用、起伏地面造成的姿态快速变化等。而ADRC将所有扰动因素视为一个“总扰动”，通过控制器中的典型算法模块将总扰动作为控制目标，实现控制的快速收敛，以期达到良好的控制效果。通过BP（Back Propa?gation） 神经网络技术对扩张状态观测器进行在线参数整定，通过引入自适应ESO的方法，提高ESO对扰动估计的精度，进而提升控制效果。BP网络典型结构如图5所示。

在复杂地形下，对环境运动中机器人的位置和姿态进行控制。控制器内外环需要进行设计，控内环控制姿态变化，外环控制位置变化。同时，外环的位置控制输出作为内环姿态控制器的控制输入。整体控制器设计如图6所示：

位置控制器根据期望位置和实际位置计算出期望总拉力fd、期望滚转角?d、期望俯仰角θd；姿态控制器根据位置控制器输出的期望偏航角ψd、实际姿态以及位置控制器的输出计算出期望力矩τd；然后，控制分配算法根据fd 和τd 计算出四个车轮的期望转速ωd，i；最后，驱动控制根据ωd，i 计算出每个驱动电机的输出功率σd，i。

3 移动机器人运动规划

机器人移动的复杂空间能够视为一个三维空间，特别是存在起伏型路面，并且移动过程中会存在一些无法通过的障碍点。当移动机器人进行巡检路径规划时，需要将不平整的起伏点、无法通过的障碍点等非通行区域进行整体规划计算[19]。根据分析，首先选择相关信息进行全局规划，生成多个路径节点，将近邻节点间做连线形成一条完整的运动轨迹，实现整体的规划路径求解。在规划算法生成路径以后，移动机器人按照指规划处的路径从第一个节点出发，根据节点依次移动，直至机器人到达最后节点。但是移动机器人在执行运动任务的过程中需要维持安全距离且要兼顾规避突发性障碍，因此需要同时结合局部动态规划来进行实时规划。

快速探索随机树（RRT）算法是运动规划和机器人学中广泛使用的算法。它最早是由Steve LaValle在1998年提出的，此后成为在静态网络中寻找最短路径的流行方法。该算法的工作原理是在存储所获得的路径数据的同时，向规划空间增量地添加随机树节点。当随机树节点满足一定约束时，停止树扩展，从终点到起点进行反向搜索，得到连接两点的完整路径。RRT的优势之一是能够处理复杂和动态的环境。该算法在解决高维状态空间的问题时尤其有效，在高维状态空间中，传统的搜索算法可能会因为维度灾难而失败。此外，RRT可以處理机器人系统中常见的非完整约束。RRT已被应用于多个领域，包括自动驾驶、机器人和电脑游戏。在自动驾驶中，RRT可以用来规划自动驾驶汽车的轨迹，避开障碍物，安全到达目的地。在机器人科学中，RRT可以帮助机器人在复杂的环境中导航，并执行抓取和操纵等任务。因此，RRT是一个有效的算法，可以在复杂和动态的环境中高效地规划路径。凭借其多功能性和灵活性，它已成为运动规划和机器人学中的基本工具，也非常适用于本文的研究内容。算法流程如图8所示。

将整个移动机器人规划的地图抽象为图的表示形式：

其中，V 是随机树中节点的集合，E 是随机树中边的集合。随机树边的和就是不同节点间的距离和。通过RRT算法求解出最优的航迹节点，可以作为前文所述控制器的路径规划生成器。这种方法可以使机器人在环境中进行路径规划，避免了碰撞和障碍物，并且不需要提前建立地图。控制器结构可以根据路径规划的需要进行更新，图7是更新后的控制器结构。

4 系统验证

移动机器人控制器性能需要设计合理的实验验证规划算法与控制律的有效性，尤其需要测试存在障碍物及起伏路面条件下的控制器与路径规划的性能与有效性。因此，基于Matlab进行了数值仿真，多个测试任务中的典型结果如图9、10所示，图9是位置轨迹变化，图10是姿态变化。

从图中可明显地看到，轨迹是平滑并且稳定的，快速经过规划后的目标位置点，在经过某些起伏路面时会发生小幅度姿态变化，总体上机器人的姿态始终是稳定的。说明控制器的控制效果达到了预期的目标，能够实现复杂地形下的快速规划轨迹及位置控制。

5 结论

针对复杂环境下移动机器人任务规划与控制，综合了环境下的起伏地形及障碍物。首先，通过牛顿- 欧拉方法建立了机器人的动力学模型，并分别建立了大地坐标系与机体坐标系。然后使用BP神经网络对ADRC控制器进行修改，完成控制器的改进，并且通过随机生成树算法开发了路径规划器，实时产生最优期望位置坐标。然后通过Matlab仿真实验证明了系统设计有效性，能够实现复杂地形下的移动任务。