薄壁箱型悬臂梁挠度计算方法探讨

袁春辉 杨继

摘要：在起重机结构设计中，薄壁箱型结构应用较多，以吊臂和支腿为典型，而吊臂和支腿设计计算中，挠度是重要的考量指标，因此薄壁箱型结构的挠度计算较为关键。据此，从理论计算和有限元计算两种方法入手，针对某个车型的具体尺寸及载荷数据分别计算不同工况下的挠度值，分析说明计算结果的差异，从而得到两种贴合实际工况的计算方式。

关键词：起重机；薄臂箱型悬臂梁；挠度计算；有限元法

中图分类号：U462  收稿日期：2023-06-10

DOI：10.19999/j.cnki.1004-0226.2023.08.012

1 前言

起重机的吊臂、支腿一般都设计为伸缩式薄壁箱型结构，类似于悬臂梁受力方式。设计中均需校核吊臂和支腿的挠度。在产品概念设计阶段，一般会根据粗算的受力情况，通过理论计算来确定截面尺寸。计算过程中发现采用不同方法得到的挠度值有一定偏差，尤其是采用初等梁理论的计算值偏差较大。

本文以某一个支腿截面为例，将支腿的受力简化为悬臂梁计算模型（图1），相关截面参数见图2，分别采用理论计算和有限元计算两种方法。理论计算时考虑了初等梁理论的挠度计算及考虑剪切变形影响的挠度计算；有限元计算则分别采用梁单元、板壳单元和实体单元三种单元得到对应结构的挠度值。

2 理论计算挠度值

2.1 初等梁理论挠度计算

参考刘鸿文撰写的《材料力学》［1］计算公式，则集中力作用下自由端最大挠度为：

2.2 考虑剪切变形效应的薄壁箱型悬臂梁挠度计算

初等梁理论未考虑剪切变形效应，对于薄壁箱型结构，需考虑剪切变形效应。考虑剪切变形效应时悬臂梁的挠度计算公式如下：

式中，G为剪切模量；Aw为箱型截面腹板面积。

2.3 薄壁箱型悬臂梁挠度理论计算值

假设悬臂梁长度为3 100 mm，自由端受集中力为100 000 N，采用上面两种方法计算得到挠度的数值如表1所示。

从表1的计算值可知，考虑剪切变形效应的挠度比未考虑此因素的挠度增大约10%，一般认为偏差大于5%属于偏差较大。

3 有限元计算挠度值

有限元计算薄壁箱型悬臂梁结构拟分别采用Beam188梁单元，Shell181板壳单元和Solid185实体单元，三者均为一阶单元，感兴趣的工程师可以试试这三种单元对应的高阶单元，计算值偏差非常小。

Beam188单元基于铁摩辛柯梁理论（图3），考虑了剪切变形效应。

对于实体模型，为避免剪切锁定，截面顶板和底板采用三层单元，如图4所示。

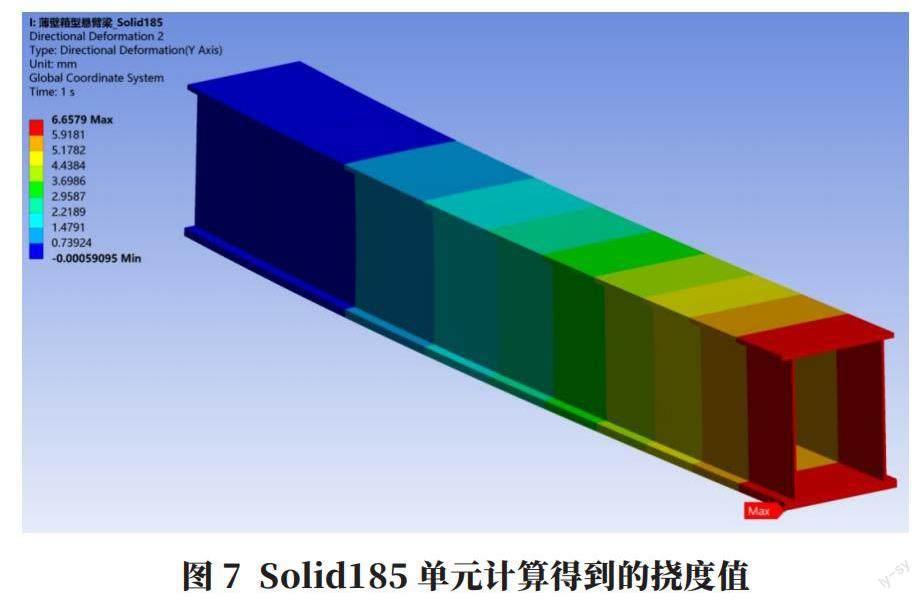
分别采用以上三种单元计算薄壁箱型悬臂梁的挠度，结果如图5～图7所示。

4 挠度计算值对比

将以上理论计算值和有限元计算值进行对比，如表2所示。

以考虑剪切变形效应得到的挠度计算值为基准值，其余4个挠度计算值均小于此值，3个有限元计算值与此值均非常接近，偏差均小于2%。

但由初等梁理论计算得到的挠度值明显偏小，后续进行挠度计算时需注意。

5 结语

起重机支腿的变形仍属于小变形范畴，基本可认为截面左右两侧对称受力，且左右腹板间距不大，为非宽箱梁，剪力滞不明显，各个截面正应力和剪应力采用初等梁理论计算公式仍有足够的计算精度。如遇变形较大的情况，偏差会变大，相关研究人员可参考刘鸿文撰写的《材料力学》及郭金琼撰写的《箱形梁设计理论》［2］分别计算后再对比结果，此处不再赘述。

参考文献：

[1]刘鸿文.材料力学[M].5版.北京：高等教育出版社，2011.

[2]郭金琼.箱形梁设计理论[M].2版.北京：人民交通出版社，2008.

作者简介：

袁春辉，男，1987年生，工程师，研究方向为起重機总体布置及其液压系统。