黄龙带水库入库水量与降水量关系研究

陈赞亮 梁铭海 刘光胜 周喜杨 高强 朱云立 毛镇南

（1 广州市北部市管水利设施事务中心，广州 510960；2 广州市水务科学研究院有限公司，广州 510230；3 北京市心中有数科技有限公司，北京 100080）

0 引言

我国地处东亚季风区，降水的空间和时间分布极不均匀，基于降水的长期径流预报是科学制定水资源调度方案、确保水利设施安全和发挥其经济效益的重要依据。黄龙带水库位于广州市从化区东北部，坝址位于流溪河支流汾田水下游，坝址以上干流长度21 km，是一座集防洪、灌溉、发电为一体的中型水库，最大库容为9458万m3，集雨面积为92.3 km2。库区雨量分配很不均匀，10月—翌年3月量少，4—9月量大。 流域洪水一般发生在4—10月，4—6月以前汛期降水和梅雨降水为主，7—10月以台风暴雨为主。流域上游为山地，河道坡降较大，发生大暴雨时，常形成陡涨陡落的大洪水，洪水历时短，洪流大。黄龙带水库的天然来水在时间（年内和年际间）上的分配极不均匀。为了充分利用天然来水径流，使其更好地发挥防洪、发电、灌溉、供水、环境调节等功能，服务社会经济发展，需要对多变的天然来水径流和水库水量进行调节。规划水库的中长期运行方式对经济效益和社会效益有重要作用。

天然径流是黄龙带水库入库水量的主要来源，主要依赖于气象条件的变化。关于径流的影响因子及预测方法已有很多研究，长期径流的预报方法通常有两大类。一类是针对径流时间序列本身进行研究， 如基于数理统计的回归分析和时间序列分析、神经网络技术、支持向量机以及贝叶斯理论等[1-4]。另一类是从影响径流的物理因素出发，通过基于物理的背景分析建立长期径流预报模型[5-6]。如刘勇等[7]从影响径流的物理因素入手，将大气环流、海水温度、历次降水和径流作为预测因子，建立了出流预测模型。冯小冲等[8]以前一年海温场、高度场及74项环流特征量等因素为预报因子，利用逐步回归方法建立了水库逐月入库径流预报模型。祝诗学等[9]运用气象遥感相关知识建立模型。秦鹏程等[10]通过相关分析建立了逐月入库水量预报模型。上述研究主要是以前期降水和径流影响因子为依据[11]，预测精度相对较高[12]。

本文通过分析黄龙带水库长期径流的变化特征，从影响径流的物理因素入手，分析径流与气象因子之间的关系，针对不同月份的入库水量对降水量的响应存在差异问题，分别建立每个月的入库水量诊断模型，为黄龙带水库的长期水量预报提供科学依据。

1 数据来源与研究方法

1.1 数据来源

本研究中数据采用黄龙带水库流域内1977—2020年坝前、联星、枫木塱三个观测站 （图1）的逐月降水数据和逐月平均入库水量数据，资料来源于黄龙带水库管理中心。三个观测站覆盖了黄龙带水库流域不同的方位，用算术平均值法计算流域降水量。

图1 黄龙带水库观测站点分布图（左上：联星观测站；右上：枫木塱观测站；左下：坝前观测站）Fig. 1 Distribution map of Huanglongdai Reservoir observation sites (top left: Lianxing Station; top right:Fengmulong Station; bottom left: Baqian Station)

1.2 研究方法

黄龙带水库流域处于东亚季风区，气候湿润，降水充沛，雨热同季。本研究选择入库水量和流域内降水量作为研究对象，以当月和前1～10个月为有效时段进行分析。首先对黄龙带水库入库水量及流域内降水量的年内分布特征进行研究，之后研究黄龙带水库降水集中度与入库水量集中度的年内分布特征，对黄龙带水库入库水量及流域内降水量之间的关系进行初步分析。为进一步揭示入库水量与降水量的关系，对月入库水量与逐月平均降水量进行相关性分析，选取与月入库水量相关性比较大的几个月份的降水量作为影响因子。由于不同月份的入库水量对降水量的响应存在差异，因此采用多元回归方程分别建立每个月的入库水量诊断模型，并采用相关系数（R）、平均绝对误差（MAE）、平均绝对误差率（MAPE）、均方根误差（RMSE）等指标[13]对模型诊断精度进行评价，最终提出一种提高入库水量诊断模型精度的方法，结合中长期和短期天气预报，为将来建立符合水文预报要求的预报模型提供参考。上述指标计算公式为：

式中，Oi为实际观测值；Si为诊断值；N为样本数。

降水集中度（PCD）计算方法为：

式中，Ri为研究时段总降水量；rij为研究时段内某候降水量；θj为各候对应的方位角；i为年份；j为候序。PCD能够反映降水总量在研究时段内各候的集中程度，PCD越大，则降水量越集中。PCP为合成向量的方位角，表示向量合成后重心指示的角度，反映日最大降水量的出现时段[14-16]，称为降水集中期。

入库水量集中度（IWCD）计算方法为：

式中，Si为研究时段总入库水量；sij为研究时段内某候入库水量；θj为各候对应的方位角；i为年份；j为候序。IWCD能够反映入库水量总量在研究时段内各候的集中程度，IWCD越大，则入库水量越集中。IWCP为合成向量的方位角，表示向量合成后重心指示的角度，反映日最大入库水量的出现时段，称为入库水量集中期。

2 入库水量与降水量的关系

2.1 入库水量及降水量的年内分布特征

图2给出了黄龙带流域逐月平均降水量的变化，黄龙带流域年平均降水量为2035 mm，其中3—9月的降水量占全年总降水量的86%，而处于前汛期的4—6月的降水量最大。图2还给出了黄龙带水库逐月平均入库水量的变化，黄龙带水库年平均入库水量9.07亿m3，其中3—9月的入库水量占全年总入库水量的76%。与降水量的高值出现在4—6月不同，入库水量的高值出现在5—7月，相较于降水量的月际变化有明显的滞后特征。

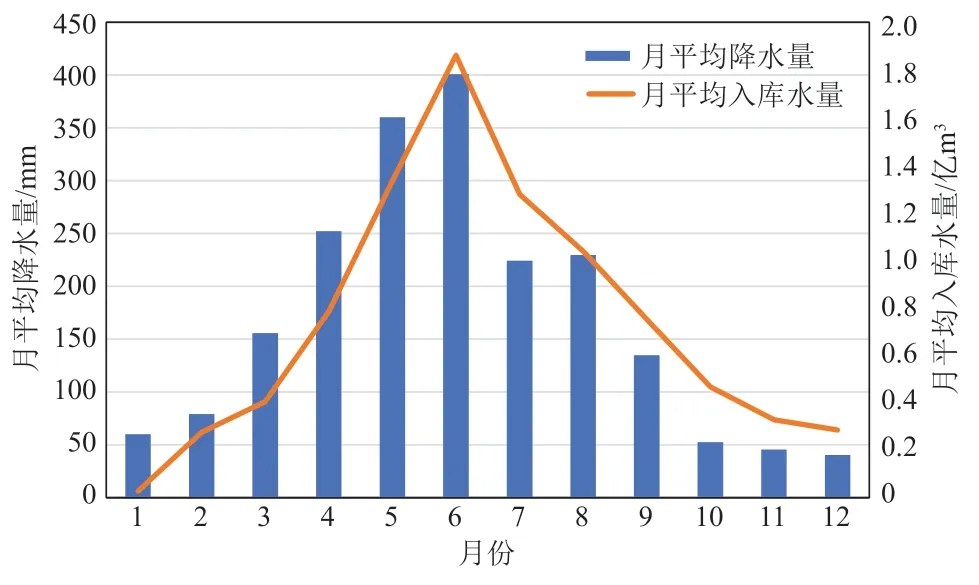
图2 1977—2020年黄龙带流域的月平均降水量和月平均入库水量变化Fig. 2 Variations of monthly mean precipitation over Huanglongdai Reservoir and its monthly mean inflow water volume from 1977 to 2020

2.2 降水集中度年内分布特征

降水的集中程度对水资源的优化调度和水库的安全具有重要影响。图3给出了黄龙带水库1977—2020年汛期的降水集中度和降水集中期年际演变曲线。降水集中度为0.064～0.620，多年均值为0.266，主要峰值年份为1977年、1984年、1986年、2005年和2008年，主要谷值年份为1979年、1982年、1985年、2013年和2016年，其中峰值年的降水集中度高（均值达0.485），降水集中度高的年份往往有集中出现强降水的情况。降水集中期大多处于5月7日—8月26日，历年均值出现在6月25日，总体呈峰、谷交替变化，并呈现出与降水集中度反向变化的特点。可以看出，广东省处于多雨带，雨季开始较早、持续时间长，在降水集中度高的年份，降水集中期早，连续性强降水多，这对黄龙带水库流域的产流会产生一定的影响。

图3 1977—2020年黄龙带水库降水集中度和降水集中期的年际变化Fig. 3 Interannual variations of precipitation concentration degree and period of Huanglongdai Reservior from 1977 to 2020

2.3 入库水量集中度年内分布特征

图4中给出了黄龙带水库1977—2020年汛期的入库水量集中度和入库水量集中期的年际演变曲线。入库水量集中度为0.254～0.636，多年均值为0.444，主要峰值年份为1986年、1993年、1998年、2005年和2008年。主要谷值年份为2003年、2004年、2009年、2011年和2016年，其中峰值年的入库水量集中度高（均值达0.590）。入库水量集中期大多处于8月5日—9月14日，历年均值出现在8月23日，总体呈峰、谷交替变化，并呈现出与入库水量集中度同向变化的特点。

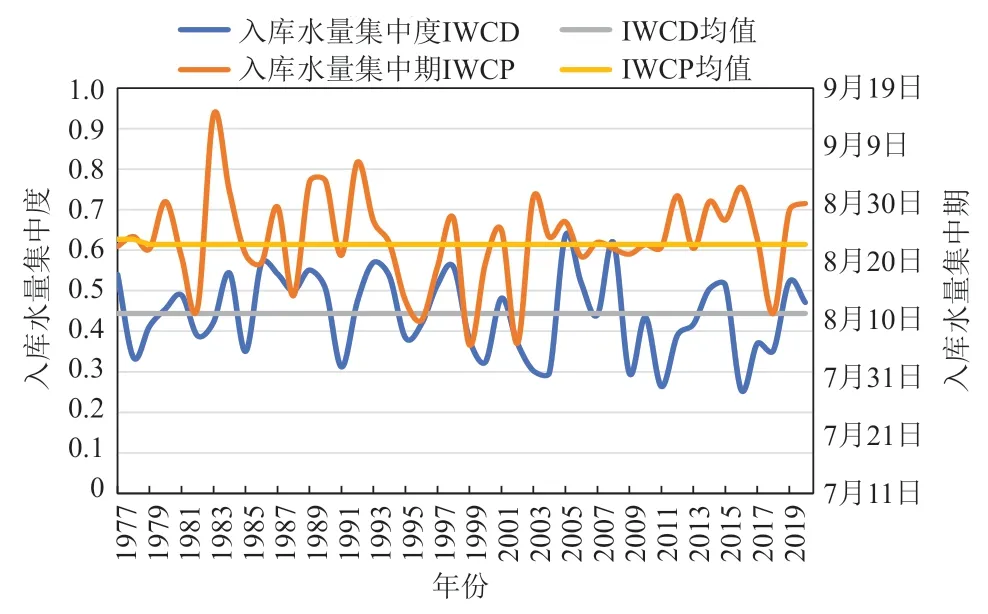
图4 1977—2020年黄龙带水库入库水量集中度和入库水量集中期的年际分布Fig. 4 Inter-annual distributions of inflow water volume concentration degree and period of Huanglongdai Reservior from 1977 to 2020

对降水集中度和入库水量集中度做Pearson相关性分析，二者相关系数为0.63（P＜0.001），说明入库水量集中度与降水集中度呈显著的正相关。即降水集中的年份，入库水量也相应集中。同时，降水集中期和入库水量集中期的相关系数为0.66（P＜0.001），说明入库水量集中期与降水集中期呈显著的正相关。结合上述分析，可以得到以下认知，黄龙带水库降水集中度和入库流量集中度较高，在降水集中期需做好防洪工作，避免对河道行洪和沿岸人民生命财产构成威胁。 关于降水集中度与入库水量集中度的高相关性，本文将在诊断模型的误差分析中做进一步讨论。

对暴雨天数与降水集中度和入库水量集中度分别做Pearson相关性分析，暴雨天数与降水集中度的相关系数为0.048，暴雨天数与入库水量集中度的相关系数为0.314（P＜0.05）。根据流域的降水数据，黄龙带流域暴雨天数少，年内分布较为随机，而流域雨季长，总降水量较多，因此少量的暴雨极端值对降水集中度的影响并不大。

2.4 月入库水量与降水量的相关性

对黄龙带水库月平均入库水量和当月以及前1～10个月的月平均降水量进行相关分析，结果如表1所示。其中，黄龙带水库入库水量与当月和前1个月的降水量关系最为显著，入库水量与降水量之间存在一定的滞后关系。7—9月的入库水量与当月和前1个月的降水显著相关，入库水量主要受这2个月份的降水量影响。值得注意的是，在3—5月以及9—10月，入库水量与当月及前2个月降水量都显著相关，这可能表明在春季和秋季，前期降水对产流的影响较大且影响时间较为持久。

表1 黄龙带水库各月入库水量与前期不同滞后时间降水量的相关系数Table 1 Correlation coefficient between the monthly inflow of the Huanglongdai Reservoir and the precipitation at different lag times in the previous period

基于此，需要对每个月份分别进行建模，这样可以更好地研究汛期与枯水期不同滞后时间对入库水量的影响，使模型的诊断结果更加精确。

3 多元回归模型的构建与验证

将入库水量与不同滞后月份的平均降水量建立逐步回归模型（表2），各月模型的调整R2平均为0.82。其中12月最低，为63.3%；6月最高，为90.8%。

表2 黄龙带水库各月入库水量诊断模型Table 2 Diagnosis models of monthly inflow volume of Huanglongdai Reservoir

表3为黄龙带水库各月入库水量诊断模型的交叉验证结果。模型的相关系数在0.79～0.95之间，除12月为0.79外，其余月份均在0.88以上，模型的拟合程度较高。各月诊断平均绝对误差是0.0174～0.128亿 m3，平均绝对误差率为11.48%～101.42%。其中1—4月的偏差最大，平均在30%以上，因为这段时期是旱季，受上游调控的影响大，诊断结果误差较大。此外，由于模型影响因子的时间尺度以月为单位，所以出现在月末的大范围降水过程由于径流产生的滞后性，并不能很好地反映在当月的径流上。以年为单位重新对误差进行评估，与实测值相关系数为0.97。相邻月份正负误差抵消后，全年诊断误差在11%以内。

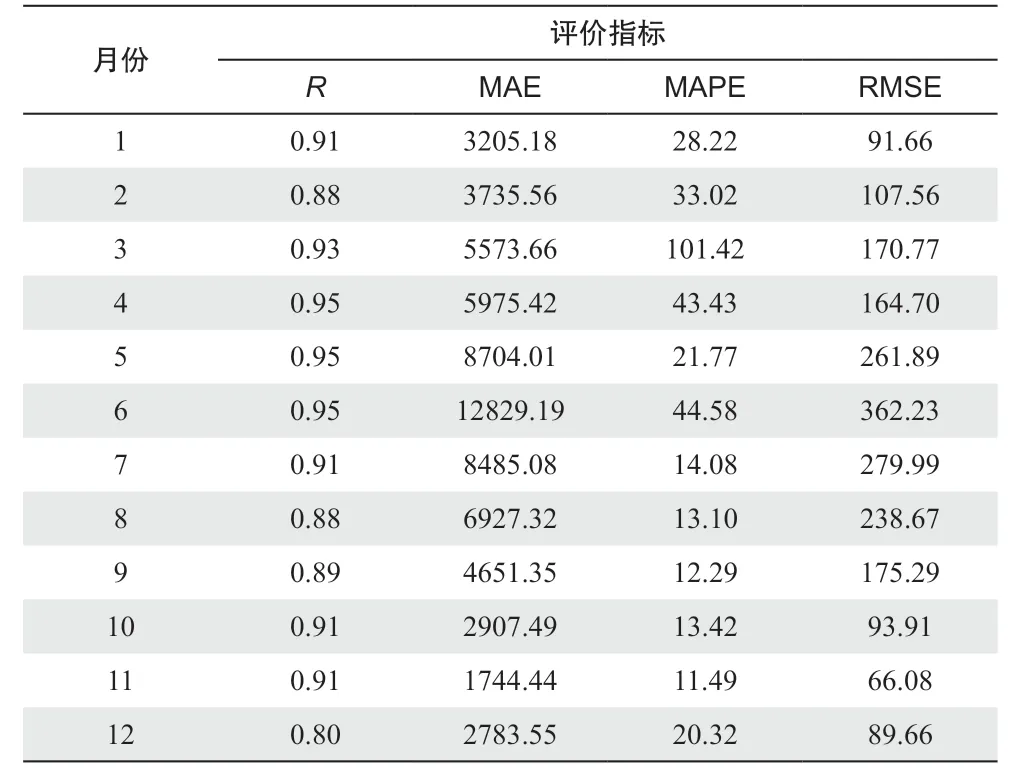
表3 黄龙带水库各月入库水量诊断模型交叉验证结果Table 3 Cross-validation results of monthly inflow diagnosis models for Huanglongdai Reservoir

4 模型误差分析

图5是以10年为尺度的诊断残差分布，代表降水量的年代际变化对入库水量的影响。箱型图中，上边缘为数据的最大值，下边缘为数据的最小值；矩形 上下边的位置分别对应数据的上下四分位数。在矩形盒内部中位数位置画一条线段，即中位线，区别开黄色矩形和灰色矩形。黄色矩形代表上四分位数与中位数之间的数据区间，灰色矩形代表下四分位数与中位数之间的数据区间。矩形面积越小，说明数据越集中；端线越长，则说明异常值越分散。如图5所示，各年代间的残差分布并不一样，但中位数分布较为平衡，其中1980—1989年与1990—1999年残差分布较为集中，异常值较少，2000—2009年异常值较多，这可能与当时的气候年际波动较大有关。

图5 1980—2019年不同年代黄龙带水库入库水量诊断残差分布Fig. 5 Residual distribution of inflow diagnosis of Huanglongdai Reservoir in different eras

图6是不同诊断偏差年份降水集中度的分布特征，代表降水的时空分布特征对诊断结果的影响。黄色矩形代表上四分位数与中位数之间的数据区间，灰色矩形代表下四分位数与中位数之间的数据区间。降水集中度在0.2～0.3的年份，诊断偏差较小，这说明模型更能适应全年降水较为平均的年份。而降水集中度偏小的年份，诊断出现正偏差的概率更大；相应地，降水集中度较大的年份，诊断出现负偏差的概率较大。这说明全年降水集中的年份，对于产流的形成更加有利，这给模型的诊断带来一定的误差。

图6 不同诊断偏差年份降水集中度分布特征Fig. 6 Distribution characteristics of precipitation concentration degree in years with different diagnosis deviations

5 结论与讨论

1）黄龙带水库流域的月降水量和月入库水量有较为明显的年内变化特征，且月入库水量与月降水量之间存在一定的滞后关系。具体来说，3—6月的入库水量与当月降水量显著相关，而3—5月以及9—10月入库水量与当月及之前2个月降水量都显著相关。这表明在汛期，当月降水对产流影响较大，而在春季和秋季，前期降水对产流的影响较大且影响时间较为持久。

2）降水集中度存在显著的年际变化特征，且与入库水量集中度存在显著相关性。

3）建立了各个月份入库水量与同期和前期降水量的线性回归模型，调整R2平均为0.82，模型具有较高的拟合能力。模型预测效果受降水集中度影响较大，降水集中度高的月份，预测结果易偏低，而降水集中度低的月份预测结果易偏高。

综上，在之后的研究中，可以将该诊断模型和其他气候模型或气候预报产品相结合，利用当月降水量的预测数据对入库水量进行实时业务预测，以满足从化地区的调水服务需求。还可以将模型进一步拓展，以季度、年度的平均降水量作为影响因子，建立季节和年度入库水量的中长期预测模型。相对于采用气象遥感相关方法建立的预测模型，本研究所建立的诊断因子优势是物理意义明确，分布特征稳定，可以充分利用最新的气候预报方法。

为最小化模型所需资料，本研究采用区域平均降水量来作为诊断变量，但是由于不同流域产流形成过程不同，降水的空间分布和时间强度不同，这些将对入库径流产生影响。除了提高预测精度外，提高降水区域和过程强度的预测精度都有利于校正预测结果。由于外部影响因素的复杂性，汛期天气预报模式的精度较低，实践中应尽可能地考虑初始条件，如河流径流等。