基于需求侧响应的分时用电计费博弈模型
向黎藜,鄢鸿婧,张人杰,段 凯,叶大勇
(1.国网重庆市电力公司营销服务中心,重庆 401120;2.北京中电普华信息技术有限公司,北京 100085)
0 引 言
近些年受环境污染问题与能源短缺问题的影响,电能作为新型的清洁能源在经济发展中起至关重要的作用。大量的调查研究表明,电力消费能够直接作用于国民经济与科学技术的发展。主体的电力系统运行包含发电、升压与降压以及配送等部分。整体运作环节如下:经过火力或水力的不同发电机组进行发电,在变电站的作用下首次升高电压,途径电网中输电的不同线路将升高的电压分解,输送过程中邻近变电站会改变电压使之降低,在配电线路中将电能配送至每一个用户。在20 世纪60 年代初期,国外已经开始研究电力的需求侧响应课题,在大型电力公司的实际案例调查中,证明企业的销售营业额与电网的需求侧响有正相关联系。后续研究中了解用户用电的分时计费标准能够满足其相应需求,使电力企业和用户之间达到共赢模式,以此作为用户用电负荷计费的控制基础策略[1]。20 世纪90 年代,国内开始对电力价格进行改革,遵循需求侧响应的管理方法,通过对电力价格变化的经济管控,刺激和引导用户完成用电时间的调整,最终形成高峰期和低谷区用电的平衡工作,完成负荷的均衡整合。本文基于需求侧响应建立用户分时用电计费的博弈模型,分析居民电力的需求响应行为,为制定有效的分时电价划分标准提供解决方案。
1 基于需求侧响应的分时用电计费博弈模型
1.1 基于需求侧响应划分用户类型
对用户类型的划分能够合理规划一段时间内的用电模式,其原因是用户在分时计费中起着至关重要的影响。作为分时计费的主体,用户能在小范围内产生一个较小的可觉差值,当用户对用电负荷没有反应时,此差值属于不敏感区域,不会对分时用电产生任何影响,但超过差值时用户会作出强烈反应,从而影响分时用电。因此,必须对用电用户进行准确划分,保证电力企业在大环境下有强大的竞争能力,根据八比二理论中表述的80%销售量来源于20%的重要客户,进行用电用户的差异性划分。大体上的用电类型可以分为商业用电和农业用电2 大类型:其中商业用电占电力市场的主体,其用电时间和用电模式较为固定,直接为电力企业产生销售营业额。而农业用电属于国家特殊性补贴用电,在用电时会产生补贴电价,对电力企业的销售额影响作用较小。通过需求侧响应原理进行用户类型的划分,其中包含3 种类型。一是按照用电量大小可以将用户分为高级用户、中级用户和普通用户,对每个用户的用电需求加以区分,对高级用户的用电需求探寻原因,可以增加电力企业的销售利润。二是根据销售渠道可以将用户分成城市用户、农村用户以及趸售用户,一般城市用户的用电需求高于后面2 个类型。三是根据用电产业划分为工业用户、商业用户以及居民住宅用户等,其中工业用电对电网的负荷会产生较大影响[2]。不同类型的用户对电价电动的作用不同,会使电价产生不一样的反应变化,从而反作用于用户的用电需求。因此,基于需求侧响应原理划分用户类型,可以将用电性质较为相近的用户规划在一个类别,作为划分峰谷电价时段的基础,从而合理确定用电的高峰时段。
1.2 确定用电峰谷时段
对用户类型进行准确划分后,需要合理确定用电的峰谷时段,由于商品受到市场和价值规律影响,电能作为电力企业的营销手段,其计费价格受用户的需求影响。电能不能储存,一旦从电力企业发出后,没有被用掉的电量就会被浪费,因此需要对用电的峰谷时段进行有效确定。为合理规划每个时段的用电需求采用模糊数学理论定义其具备条件:一是峰谷时段必须满足供电公司和用户之间的共赢局面;二是该峰谷时段必须能够准确反映供电的负荷曲线;三是峰谷时段不能出现倒置现象,其峰值与谷值的比值必须合理。在3 个必备条件规范下,就可以将电量负荷曲线的取值点进行描述[3]。根据客观守恒定律和事实存在的评断标准,当某点的峰值处在某一时段的概率超过95%,此时该位置发生谷值时段的概率基本为0,那么此刻的位置点就可以确定为峰值时段的最高点。当某点的谷值处在某一时段的概率超过95%,此时该位置发生峰值时段的概率基本为0,那么此刻的位置点就可以确定为谷值时段的最高点。当某点的峰值处在某一时段的概率等于50%,此时该位置发生谷值时段的概率也在50%,那么此刻的位置点就可以表示为峰值与谷值的平行时段。
1.3 求解分时用电报价函数构建博弈模型
一般情况下用电量的转移和各个时段的电价差成正比关系,同一时段的电价差值在超过饱和区或者低于饱和区时,用电负荷不会发生转移。对上述划分好的用电峰谷时段的用电价格加以调整,利用报价函数求解的方法构建博弈模型,从而达到削峰填谷平衡负荷的目的。假设一天内的峰谷时段划分为z个集合,每个集合内存在该时段的最高值za和最低值zb,为准确地对每个集合内的电力负荷情况加以说明,在集合中增加电力的回购单位成本j,建立用电的约束条件
式中:xi为合理性参数,即保证电力公司在改变电价时,用户的利益能够不受损害;kd为每个时段的标准电力报价;xi的取值必须在约束条件中[0,1]的区间范围,如果取值数据过小其产生的回购单位成本增加,会造成用户的用电报价增加,如果取值过大则电力企业会增加回收电量的剩余成本。在约束条件建立后,通过电量负荷布置策略求解分时用电报价,该目标函数w表达式为
式中:α和β分别为峰谷时段最大值与最小值的调度因子;回购单位成本j的最大值为划分时段的最大耗电阈值。在计算过程中αza与βza的比值结果会影响函数的最终结果,在调度因子作用下,当时段内峰值差为负数时,判断该函数处于峰时段,即可执行标准用电计费模式,反之需要重新对用电时段的峰谷时段进行划分,重新计算函数报价[4,5]。根据需求侧响应理论完成正确划分,最终完成求解价格函数的博弈模型构建。
2 实验论证分析
2.1 数据准备
为验证本文设计的博弈模型具有实际应用效果,结合具体案例进行测试,分别对电网的最大负荷、最小负荷以及峰谷负荷差值进行优化,完成均衡负荷的优化目标。本次实验在某省电力公司的电力数据中,选取具有代表性的大型工厂的日负荷数据,以24 h 的用电详细情况作为实验数据样本,具体数据如表1 所示。
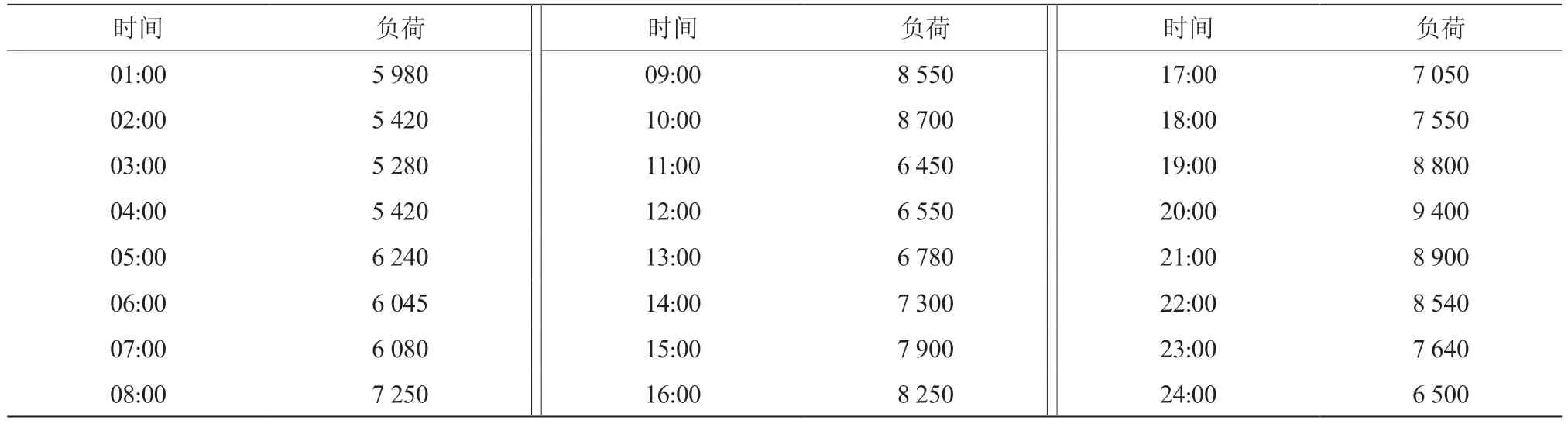
表1 某省大型工厂的日负荷数据 (单位:kW)
由表1 数据可知,该工厂一天之内的最大负荷为9 400 kW,最小负荷为5 280 kW,计算2 者差值得出峰谷差负荷为4 120 kW。利用本文设计的模型对该样本数据优化,从而完成该工厂的电网系统最优目标。
2.2 优化结果分析
根据样本数据进行负荷曲线比较,验证本文模型能够完成3 个目标值优化。目标一是最小化电网负荷的系统峰值,目标二是最大化电网负荷的谷值,目标三是最小化电网负荷的系统峰谷差值。依次对3 个目标进行优化,具体负荷曲线如图1 所示。

图1 3 个目标优化曲线
根据图1 优化结果可知,与原始数据曲线相比,优化后的曲线最大负荷为9 150 kW,减少了350 kW;最小负荷为5 800 kW,提高了520 kW;峰谷差值为3 350 kW,减少了770 kW。由此可见本文模型能够实现削峰填谷的目标,使用电负荷更加均衡,具有一定的实际应用效果。
3 结 论
本文运用博弈模型完成分时用电计费的研究,根据不同类型的电力用户用电情况,对每一类别的用电用户的高峰段用电进行标定,最终完成计费博弈模型的构建。在实验过程中证明本次构建的模型能够对用户的用电峰谷时段进行均衡调配,提高能源的利用率。但分时用电计费的制定并非一劳永逸,需要在不断调整的过程中根据电力公司自身的电力成本,完成负荷曲线的调整控制。因此,本文设计的模型仅为一个简单的计费博弈模型,只能在电价自身的弹性特性中对电力需求进行调整。后续研究过程中需要对分时用电的效果进行有效评估,为完善高峰与低谷时段的电价提供更有效的解决策略。

