基于曲波压缩的重磁异常三维反演及其应用

张恒磊，耿美霞，胡祥云*

（1.中国地质大学（武汉）地质探测与评估教育部重点实验室，湖北武汉 430074； 2.中国地质大学（武汉）地球物理与空间信息学院，湖北武汉 430074； 3.哈利法科学技术大学，阿联酋阿布扎比 127788）

0 引言

随着研究不断深入，根据重磁异常计算地下物性（密度、磁性）分布的反演方法在地质勘查［1-5］与深部构造［6-12］等领域广泛应用。前人围绕反演算法开展了深入研究，取得了一系列研究成果［13-15］，不断丰富、完善重磁反演理论体系。由于三维反演的对象是面积性重磁异常，数据量远远大于剖面反演，巨大的核函数存储需求是制约重磁三维反演实践应用的难题之一。比如：对于数据量为100×100 的观测数据，若模型剖分网格数为100×100×50，其双精度核函数的内存需求约为37 GB［16］；对于一个数据量为200×200的观测数据，若模型剖分网格数为200×200×100，其双精度核函数的内存需求高达1192 GB，远远超出目前普通计算机的硬件配置。针对重磁异常三维反演，国内外学者开展了广泛的研究。姚长利等［16］提出独特的核函数等效压缩存储技术，降低存储需求，提高反演效率，为三维重磁异常遗传反演算法和随机子域算法提供了有效技术途径；陈召曦等［17］提出基于GPU 的任意三维复杂形体重磁异常快速正演方法，极大地缩短了计算时间，为三维重磁数据快速反演奠定了基础；李泽林等［18］提出了数据空间磁异常模量三维反演方法，降低剩磁影响；戴世坤等［19］提出一种空间—波数混合域数值模拟方法，明显提高了三维重力异常正演效率；袁洋等［20］基于Toeplitz 结构矩阵提出三维模型磁场快速正演方法。学者们主要从核矩阵小波压缩［21］以及核矩阵的结构性特点［22］等角度出发，研究快速三维反演方法。小波压缩反演算法在实践中应用广泛，但鲜有关于压缩率如何影响反演精度的讨论。大规模重磁数据的三维反演对计算机硬件要求较高，因而在实践中大多尽量采用较少的三维剖分网格数量，通常为3000～50000［9，23-37］。

本文针对海量重磁异常数据压缩反演开展研究，提出了基于曲波压缩的重磁异常三维反演方法，分析了不同压缩率时小波压缩与曲波压缩对重磁异常三维反演的影响。结合理论分析与较大规模数据（模型剖分网格数为50 万）的反演测试，指出在相似反演效果条件下，基于曲波压缩的重磁异常三维反演可以实现更小的压缩比，有助于提高大规模重磁异常的三维反演效率。

1 方法原理

1.1 重磁异常三维反演

重磁异常三维物性反演通常是将地下空间划分为若干小长方体，每个长方体的物性参数值不同，由观测数据反演每个小长方体的剩余密度或者磁化强度（或磁化率）。其正演问题可以表示成如下形式

式中：N表示观测点总数；M表示剖分长方体个数；m表示剩余密度或磁化强度；d表示观测异常；Ai，j是核矩阵A的元素，表示第j个长方体对第i个观测点处产生的异常响应。式（1）可表示成矩阵形式

反演问题即是寻找一个合适的模型，使该模型的正演异常与实际观测异常达到一定的吻合度，同时还需考虑反演模型符合地质构造规律。一般目标函数可表示为

式中：φd表示数据拟合差；φm表示模型粗糙度；α为正则化因子，作用是平衡数据与模型的权重。Li等［38-39］提出采用有限差分计算模型粗糙度

式中：Wx、Wy、Wz分别表示x、y、z方向的有限差分算子；Ws表示单位矩阵；ax、ay、az、as是权系数。可见，过小的正则化因子有助于拟合观测数据，但模型粗糙度大，导致反演结果偏离真实值；而较大的正则化因子使得反演结果过于平缓而偏离观测数据［21，40］。三个方向的权系数ax、ay、az相对于as的大小直接影响反演结果沿该方向的平滑性［38-40］。为了保证反演效果的可对比性，本文统一取正则化因子α=0.1，加权因子ax=ay=as=1，az=0.1。

根据上述公式直接反演得到的密度或磁化强度趋于地表而不是按照异常体的真实深度分布，即重磁反演的“趋肤效应”，这是由于构造模型的核函数是线性的，重磁异常幅值随着距离增大而快速衰减，核矩阵元素的值随深度增加而急剧减小。因此，可以通过引入深度加权函数来克服核函数随深度增大的衰减特征，以降低“趋肤效应”。Li等［38-39］在重磁异常反演中引入深度加权函数

式中：z为块体单元中心点埋深；z0表示深度加权控制参数，其值取决于块体单元的尺寸以及观测面的高度；β为深度加权因子，磁异常反演取β=3，重力异常反演取β=2。

此外，考虑重磁反演的体积效应，本文采用统一的约束条件：将每次反演迭代中小于模型增量最大幅值20%的部分归零，也即忽略模型增量中的小幅值参数，使得反演结果趋于模型真实位置。

1.2 小波压缩核函数

在三维反演中，核矩阵A对内存的需求随着模型数量的增大而迅速增大，这也是制约三维反演应用的重要因素之一。比如对一个32×32 的网格数据体，以等网格距方式将模型剖分为20层，则双精度矩阵A对内存的需求是0.2 GB；对于一个100×100 的网格数据体，以等网格距方式将模型剖分为100层，则双精度矩阵A对内存的需求是74.5 GB，考虑解反演方程（式（2））涉及AT以及ATA等矩阵的计算与存储，其运算量远超普通计算机的性能。为了减小矩阵A的存储需求，Li等［21］提出了小波压缩

式中X表示小波变换算子，其转置矩阵XT即是小波逆变换算子。根据Li等［21］的研究成果，本文采用db4 小波进行分析和对比。

本文定义压缩后核矩阵A中非零元素个数与原核矩阵非零元素总数之比为压缩比K。基于小波的稀疏表达性能，Li等［21］指出可以将核矩阵A压缩至原有的10%左右，即K=0.1。

1.3 曲波变换压缩核函数

前人研究表明，因小波仅能表示水平、垂直和对角三个方向的特征，它适于处理点畸奇信号，而难以处理线畸奇信号。曲波变换是一种多尺度变换，是小波变换的扩展，是具有方向性的小波，能够对数据更好地进行稀疏表达［41］，因此有助于保持信号中的细节特征，在地球物理信号去噪、大地电磁二维反演中的边缘刻画等领域得到广泛应用［42-52］。

曲波变换是将信号f(x)与曲波函数φ(x)在二维空间R2内进行卷积得到曲波变换系数［41-42］

因此，与小波变换的系数分布特征相似，曲波变换系数中较大的部分表示有效信号的能量。本文将曲波变换引入重磁异常三维反演，用以压缩核矩阵规模，即根据给定的压缩比K，将小于K的系数置零，达到矩阵压缩的目的。

针对小波压缩和曲波压缩在核矩阵压缩精度、正演精度及反演效果三个方面的差别，设计如下试验进行对比分析。将模型空间剖分为14637 个水平分布的棱柱体，其中心深度均为200 m，棱柱体大小为20 m×20 m×20 m，磁化强度为1 A/m，地磁场倾角、偏角分别是-1.7°、-2.0°。图1 是包含119 个测点（观测面z=0）的南北向剖面磁异常响应核矩阵A（矩阵规模119×14637）及其正演磁异常（d=A×m）的剖面显示。

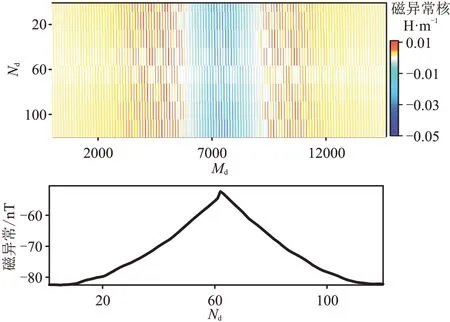
图1 核矩阵A（上）及其正演计算的磁异常（下）

图2表示不同压缩比（K=0.10，0.05，0.02）时的压缩效果。可以看出，曲波压缩误差显著小于小波压缩误差。当K=0.10时，小波压缩和曲波压缩都可以较好地恢复核矩阵，核矩阵压缩相对平均误差分别为1.06%、0.61%（图2a）；当K=0.05时，压缩结果出现一些畸变，相对平均误差分别为4.01%、1.19%（图2b）；当K=0.02 时，两种方法的压缩核矩阵均出现较大误差（图2c），相对平均误差分别为12.72%、2.95%，尤其是小波压缩损失了很多核函数的变化特征（如图2c中的局部放大图）。

图2 K=0.10（a）、0.05（b）、0.02（c）时核矩阵压缩效果

图3 为对不同压缩比的结果进行正演得到的磁异常及其误差（正演值与真实值之差），可见当K=0.10、0.05、0.02时，小波压缩所对应的相对误差分别是1.46%、5.34%、22.19%，曲波压缩对应的相对误差分别是0.29%、1.30%、4.63%。因此，采用曲波压缩能够更好地保持核矩阵压缩精度及异常的正演精度，在K取值较小时（比如0.05，0.02），其压缩效果显著优于小波压缩。

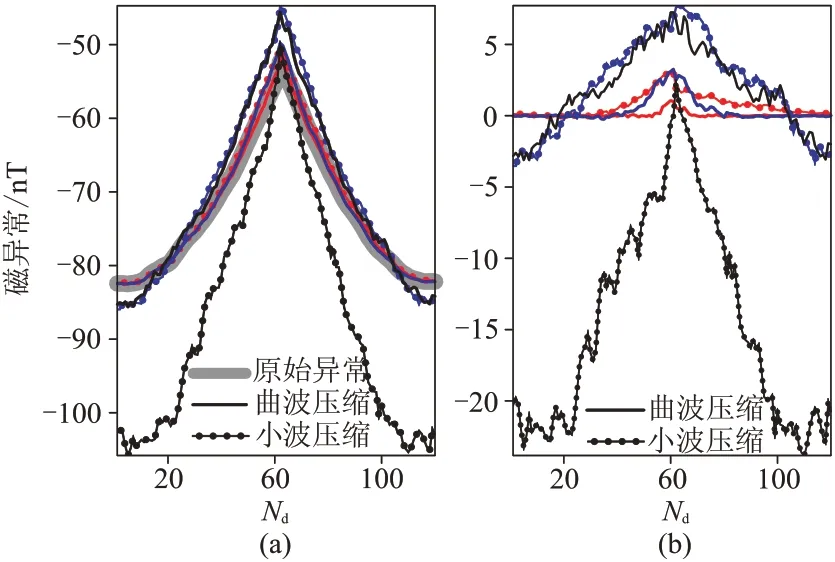
图3 不同K 时的磁异常正演曲线（a）及误差（b）

2 理论模型压缩反演

为验证本文方法的压缩反演效果，设计图4 所示的磁异常模型：模型网格数为100×100，网格间距为20 m；地磁倾角为45°，地磁偏角为0°；两个铁矿体A、B分布于向斜两翼，其上顶埋深分别为200、300 m。不考虑剩磁，该模型产生的磁异常最大值约为1100 nT。

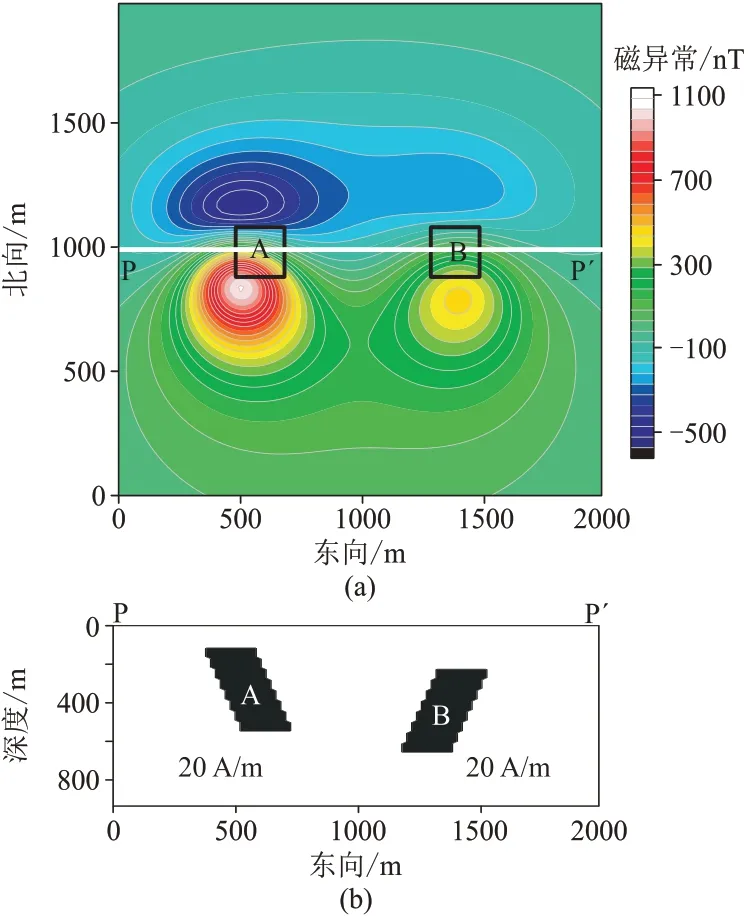
图4 理论磁异常模型示意图

为研究地质体在地下空间的三维分布特征，将地下空间剖分为100×100×50 个三维网格，剖分单元为边长20 m 的立方体。据此得到核函数A和AT的双精度存储量约为74 GB，ATA双精度存储量也为74 GB。分别采用Li等［21］的小波压缩算法及本文曲波压缩算法进行反演，取K=0.04，即存储双精度的A和AT仅需要占用内存2.96 GB。反演在内存为16 GB、主频为2.4 GHz 的笔记本电脑上运行。30 次迭代反演用时3.3 h，迭代均方根误差（RMS）见图5，基于小波压缩和曲波压缩结果反演的磁化强度分布见图6。

图5 图4 模型反演迭代均方根误差曲线

图6 图4 模型分别基于小波压缩（上）和曲波压缩（下）

从图5 可以看出，基于两种方法压缩结果的正演拟合都可以较快速地收敛于观测数据，曲波拟合精度稍优于小波压缩。当压缩比较低（K=0.04）时，由于小波压缩引起的核函数能量损失，反演结果存在显著的拖尾振荡现象（图6上）；相对而言，基于曲波压缩的反演结果具有较高的反演精度，没有出现显著的畸变（图6下）。

考虑Li等［21］在小波压缩反演中采用的压缩比为0.12，其反演结果较光滑，因而不存在图6（上）的锯齿振荡现象。为了分析该锯齿振荡是否由较低压缩率引起，对图4模型采用压缩比为0.10进行小波压缩反演（存储双精度的A和AT需要内存7.4 GB），在戴尔PowerEdge-T640 工作站上开展计算，用时约12 h。反演结果沿PP′剖面的垂直切片如图7 所示，可见与图6b 下较相似，因此可认为图6b 上的锯齿现象是由较低的压缩比导致信息失真引起的。

图7 图4 模型基于小波压缩反演的磁化强度PP′剖面

3 应用实例

根据中国西部尕林格铁矿勘探区的前期地质、钻探研究结果，该区为富铁矿集区，磁异常ΔT分布见图8a。该区岩矿石磁性特征相对简单：浅部150～200 m 巨厚的第四系覆盖层无磁性，强磁性铁矿体（磁化率为6.296 SI）主要赋存于无磁性或弱磁性的安山岩、透辉石矽卡岩（磁化率为0.005～0.013 SI）中，呈透镜状、斜列平行产出（图8b）［53］，为磁法勘探提供了良好的前提条件。该区地磁场倾角为56.5°、磁偏角为0.2°，磁异常南侧为正，北侧伴生负异常，呈北西西走向。前期见矿钻孔与未见矿钻孔难以揭示矿体位置。该区磁性体剩磁特征不明显［54］，因而本文不考虑剩磁。

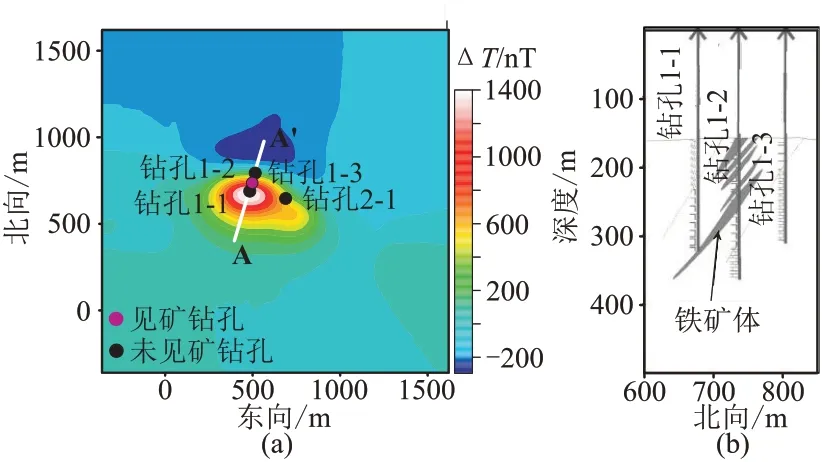
图8 尕林格铁矿勘探区磁异常ΔT（a）以及钻孔剖面（b）

前期通过改进的Euler 反褶积［53］、基于深度约束的化极磁异常边界识别Tilt 方法［54］等厘定了该区磁异常分布及矿体平面位置、埋深等信息（图9）。推测除主异常①外，在测区东部存在次级异常②。由于该区异常平缓，Euler 反褶积对两个地质体未能进行明确的区分，有关矿体的三维空间分布及矿体磁性特征亟待深入研究。

图9 尕林格铁矿勘探区基于深度约束的化极磁异常边界识别结果（彩色底图为Tilt）及改进的Euler 反褶积结果（图中散点）

图8a 显示的磁异常网格数为100×100，网格间距为20 m（东西向坐标范围为-360～1620 m，南北向坐标范围为-360～1620 m）。地下三维空间剖分为100（东西向）×100（南北向）×50（纵向）个网格单元，单元边长均为20 m。分别采用小波压缩算法和本文曲波压缩算法进行反演，取K=0.03（存储双精度的A和AT仅需内存2.22 GB），在内存为16 GB、主频为2.4 GHz 的笔记本电脑上运行。30 次迭代反演用时约2.5 h，迭代均方误差见图10。

图10 尕林格铁矿勘探区反演迭代均方根误差曲线

为了直观地反映并比较磁异常的分布特征，截取了 AA′剖面（位置见图8a），基于小波压缩和本文曲波压缩数据的反演结果分别见图11a、图11b。可以看出，两种方法在300 m 以浅区域呈现相似的磁化强度分布特征，在300 m 以深的区域小波压缩反演结果显示出较强的磁化强度异常。该深部异常是客观存在的，还是较小的压缩比导致压缩失真而引起的反演畸变？为了解答这个问题，采用K=0.10重新进行反演（存储双精度的A和AT需要占用内存7.4 GB）。考虑矩阵计算量较大，在戴尔PowerEdge-T640 工作站上运行，用时约13 h。反演结果见图11c。可见，较大压缩比（K=0.1）下的小波压缩反演结果与较小压缩比（K=0.03）下的曲波压缩反演结果相似，没有发现深部异常体。因此，图11a 中的深部磁化强度异常是由于小波压缩采用了较小的压缩比（K=0.03）导致信号失真而出现的虚假异常。

图11 尕林格铁矿勘探区三维磁化强度反演结果沿AA′剖面的垂直切片

图12 是基于两种压缩数据的磁化强度反演结果在260 m 深度（主矿体深度）上的水平切片。可以看出，基于曲波压缩数据的三维反演即使在较小的压缩比（K=0.03）下依然可以保持较稳定的反演结果，反演结果的异常形态与采用较大压缩比的小波压缩数据反演结果相似，可清晰地反映旁侧异常圈闭②。

图12 尕林格铁矿勘探区磁化强度三维反演结果在260 m 深度上的水平切片

4 结论

自小波压缩引入重磁异常三维反演，重磁三维反演快速发展并广泛应用于地质勘查、深部地球物理等领域，不断有学者从计算效率和反演效果两个方面推陈出新，发展了一系列重磁三维反演方法，其中小波压缩反演方法被国内外学者广泛应用并商业化。尽管如此，较大的核矩阵计算难题依然是制约海量重磁异常三维反演应用的瓶颈，也是当前学者关注的热点问题之一。本文从稀疏压缩的角度出发，将曲波变换应用于重磁异常三维反演的核矩阵大规模压缩，着重讨论了传统小波压缩反演方法与曲波压缩反演方法在压缩率与压缩精度方面的差别，分析了较小压缩比时反演失真的原因，指出相对于传统小波压缩反演10%的压缩比，曲波压缩反演在3%～4%压缩比时仍能保持较好的反演稳定性，即便普通计算机亦能支持大规模的三维反演，推动重磁数据三维反演的实用化。

感谢加州理工学院应用和计算数学中心Curve-Lab 实验室提供曲波变换源代码！