卷烟物理指标综合测试比对方法的研究应用
田 晶,贺 韧,李文华,尚 华,张家芹,王凌云,陈 佳
(湖北中烟工业有限责任公司,湖北 武汉 430040)
0 引言
卷烟物理指标包括卷烟质量、圆周、长度、吸阻和硬度等,直接决定了卷烟质量的好坏。卷烟综合测试台集成多个测量单元,能同时测量上述指标,在卷烟生产工序自检、过程专检和成品入库检验等环节有着广泛的应用。由于各检测环节的综合测试台测量结果存在一定差异,若这种差异不能控制在有效范围内,将导致不同仪器对同一样品的测量结果出现较大偏差,影响生产企业质量控制。为保证多道检测环节测量结果的准确性和一致性,应定期开展仪器比对,监测仪器检测结果的有效性,保证产品质量的稳定。
仪器比对是指由同一操作人员,在相同的试验环境下,采用不同的检测仪器对同一样品进行的测试,通过对检测结果一致性的分析,评价仪器对检测结果的准确性和可靠性的影响[1]。如何采用合适的方法分析比对结果,识别不同检测仪器测量结果的差异性,是比对工作中的关键所在。仪器比对是一项保证卷烟厂各检验环节测量结果准确性和一致性的有效手段,也是保障产品质量稳定的重要方式。因此,必须使用合适的比对方法对仪器测量结果的差异性进行评价,从而检验仪器测量结果的有效性,确保检测工作质量。目前,卷烟厂技术人员多凭经验或简单比较平均值、极差的方法粗略估计仪器比对结果之间的差异,由于样本数据总会存在误差,不能简单通过样本统计量数值的大小直接对总体做出判断,必须使用严谨合理的统计分析方法。尹本涛等人[2]采用建立线性回归方程的方式对卷烟综合测试台进行比对。施亮星等人[3]基于多元分析法对卷烟物理指标综合测试系统能力进行对比评价。范胜兴等人[4]采用MSA 测量系统分析对各综合测试台测量结果差异性进行分析。袁丹宇等人[5]采用归一化偏差法评价综合测试台比对结果。上述方法虽然可以对仪器比对结果进行分析,但存在计算量大、方法复杂等缺点。假设检验作为一种根据样本数据来推断总体特征的方法,通过事先对总体做出某种假设,再根据样本数据,运用统计分析的方法对假设进行检验和判断[6-7],可以科学评价参比仪器测量结果之间是否具有显著性差异,从而获得科学可靠的结论和决策,操作简单、方便使用,可以应用在综合测试台比对结果评价中。
根据卷烟厂仪器比对的现状,采用F 检验、t 检验、单因素方差分析、Tukey 多重比较等假设检验方法,分别对2 台五功能综合测试台和3 台三功能综合测试台的比对结果差异性进行评价,建立了2 台及多台综合测试台比对方法,该比对结果评价方法同样适用于卷烟厂水分仪、烘箱等仪器比对。
1 比对方法
1.1 选定基准仪器
进行仪器比对时,首先要确认1 台仪器作为基准仪器。基准仪器应具备以下特征:测量准确性相对较高,必须检定、校准合格,经过量值溯源。通过比较基准仪器与比对仪器对同一样品的测量结果,评价比仪器测量结果的准确性和一致性。如果不确定基准仪器,则只能检验各参比仪器测量结果有无显著性差异,即测量结果的一致性,不能直接判断各仪器测量结果的准确性。也可以使用烟支物理检测溯源比对棒作为标准物质,用来检验测量结果的准确性。
1.2 参比仪器
参比仪器必须是同功能、检测精度相同的仪器,比对试验开始前应对所有参比仪器统一进行预热和校准。
1.3 比对样品
将卷烟样品作为比对样品,卷烟样品取自卷烟厂生产现场机台,当卷烟机运行平稳后,于卷接机出口处一次性抽取足够数量的卷烟,卷烟样品必须是经检查无外观质量缺陷,不影响其物理指标检测结果,并在温度22±1 ℃,湿度60%±3%环境条件下平衡48 h。
1.4 比对方法
取30 支卷烟样品为1 组比对样品,分别在基准仪器和比对仪器上进行测试,测试环境条件满足温度22±2 ℃,湿度60%±5%。
2 比对结果评价
2.1 F 检验和t 检验
当参比仪器数量为2 台时,即基准仪器和比对仪器各1 台时,采用F 检验和t 检验对比对结果进行评价,先通过F 检验判断2 台仪器测量数据的方差是否相等,若方差相等,再进行t 检验,等方差性是能够使用t 检验的前提。
2.1.1 F 检验
F 检验也称方差齐整性检验,用于判断2 台仪器的精密度即随机误差是否具有显著性差异[8]。首先,建立原假设H0:2 台仪器检测数据的方差相同(σ12=σ22),备择假设H1:2 台仪器检测数据的方差不同(σ12≠σ22),双边假设检验,选定显著性水平σ 为0.05,F 统计量计算公式如下:
式中:S12、S22分别为2 台仪器测量数据的标准偏差,F 服从第一自由度f1=n-1,第二自由度f2=m-1 的F分布,其中n、m 分别为2 个样本的容量。原假设的拒绝域为{F<Fα/2(n-1,m-1) 或F>F1-α/2(n-1,m-1)},若F 值落入拒绝域,则拒绝H0,接受H1,说明2 组检测数据的精密度即随机误差有显著性差异,比对结果不满意;若统计量F 值未落入拒绝域,则接受H0,拒绝H1,说明2 组检测数据的精密度一致,可继续使用t 检验。
2.1.2 t 检验
t 检验用于判断2 台仪器测量数据的均值是否具有显著性差异,评价2 台仪器测量结果一致性。建立原假设H0:2 台仪器测量数据的均值相同(μ1=μ2),备择假设H1:2 台仪器检测数据的均值不同(μ1≠μ2),双边假设检验,选定显著性水平α 为0.05,t 统计量计算公式如下:
2.2 单因素方差分析和多重比较检验
实际工作中,参比仪器数量通常为3 台及以上,即1 台基准仪器,多台比对仪器,对于3 台及以上仪器测量结果的差异性分析,使用单因素方差分析法进行显著性检验。
2.2.1 单因素方差分析
单因素方差分析又称一元方差分析,是讨论一种因素对试验结果有无显著性影响[9]。设某单因素A有r 种水平,每种水平下的结果服从正态分布,在各水平下分别做了ni(i=1,2,…,r) 次试验,任一试验数据可以表示成xij(i=1,2,…,r;j=1,2,…,ni),i 表示因素A 对应的水平,j 表示在i 水平上的第j 次试验。
令xi为第i 种水平上所有试验值的算术平均值,称为组内平均值,即:
各测量结果之间存在差异,这种差异可以用离差平方和表示,其中,总离差平方和用SST表示,反映了试验结果之间存在的总差异,计算式为:
组间离差平方和可以用SSA表示,反映了各组内平均值i之间的差异程度,这种差异是由于因素A不同水平作用造成的,计算式为:
组内离差平方和可以用SSe表示,反映了在各水平内,各试验值之间的差异程度,这种差异由随机误差产生,计算式为:
3 种离差平方和存在如下关系:SST=SSA+SSe,这说明试验值之间的总差异来源于2 个方面,一方面由于因素水平不同造成的,如采用不同检测仪器得到测量结果不同,这种差异是系统的;另一方面是由于试验的随机误差产生的,如检测仪器本身重复测量,测量结果也不一定相同。
由离差平方和的计算公式可以看出,试验数据越多,计算出来的离差平方和就越大。因此,为消除数据个数及因素水平数的影响,用离差平方和除以对应的自由度可得到均方和,其中MSA=SSA/dfA,MSe=SSe/dfe,MSA为组间均方,MSe为组内均方。
方差分析的基本思想就是求出组间均方与组内均方之比值,这个比值称为F 统计量,即:
它服从自由度为(dfA,dfe) 的F 分布,F 统计值越大,说明因素效应越显著,对于给定的显著性水平α,如果F>F1-α(dfA,dfe),则认为因素对试验结果有显著性影响,即不同仪器测量结果之间存在显著性差异,否则认为不同仪器测量结果之间没有显著性差异。
2.2.2 多重比较法
方差分析可以检验不同仪器测量结果之间是否存在显著性差异,但不能分析存在的显著性差异是每台仪器之间都有显著性差异,还是仅在几台仪器之间存在显著性差异。因此,还需多重比较检验,对不同仪器进行两两比较[10]。多重比较需在方差分析结果存在显著性差异的前提下进行,若方差分析结果不存在显著性差异,则无需进行多重比较。可通过Minitab 软件对数据进行Tukey 多重比较检验。
3 综合测试台比对试验实例
3.1 综合测试台比对方法
3.1.1 2 台五功能综合测试台比对
选取卷烟物理检测室2 台五功能综合测试台(Borgwaldt KC),编号分别为1#、2#,每台配备质量、圆周、长度、吸阻、硬度5 个测量单元,其中1# 五功能测试台为基准仪器。选取外观质量合格,平衡48 h 后的卷烟样品,30 支为1 组,共2 组,分别在1#、2#五功能综合测试台上测试,比对结果进行F 检验和t 检验。
3.1.2 3 台三功能综合测试台比对
选取工序自检、过程专检、入库检验3 个检验环节的三功能综合测试台(Borgwaldt KC) 各1 台,总共3 台,编号分别为3#、4#、5#,每台配置质量、圆周、吸阻3 个测量单元,其中5#三功能测试台为基准仪器。选取外观质量合格,平衡48h 后的卷烟样品,30 支为1 组,共3 组,分别在3#、4#、5#三功能综合测试台上测试,比对结果进行单因素方差分析和多重比较。
3.2 结果与分析
3.2.1 2 台仪器比对结?果差异性分析
对1#、2#五功能综合测试台进行测量,对其测量结果进行F 检验和t 检验。
(1) 2 台比对仪器测量结果精密度差异分析。计算1#、2#五功能综合测试台各测量单元测定结果的F 统计量。
五功能综合测试台测定结果F 统计量见表1,五功能综合测试台测定结果见表2。

表1 2 台五功能综合测试台测定结果F 统计量
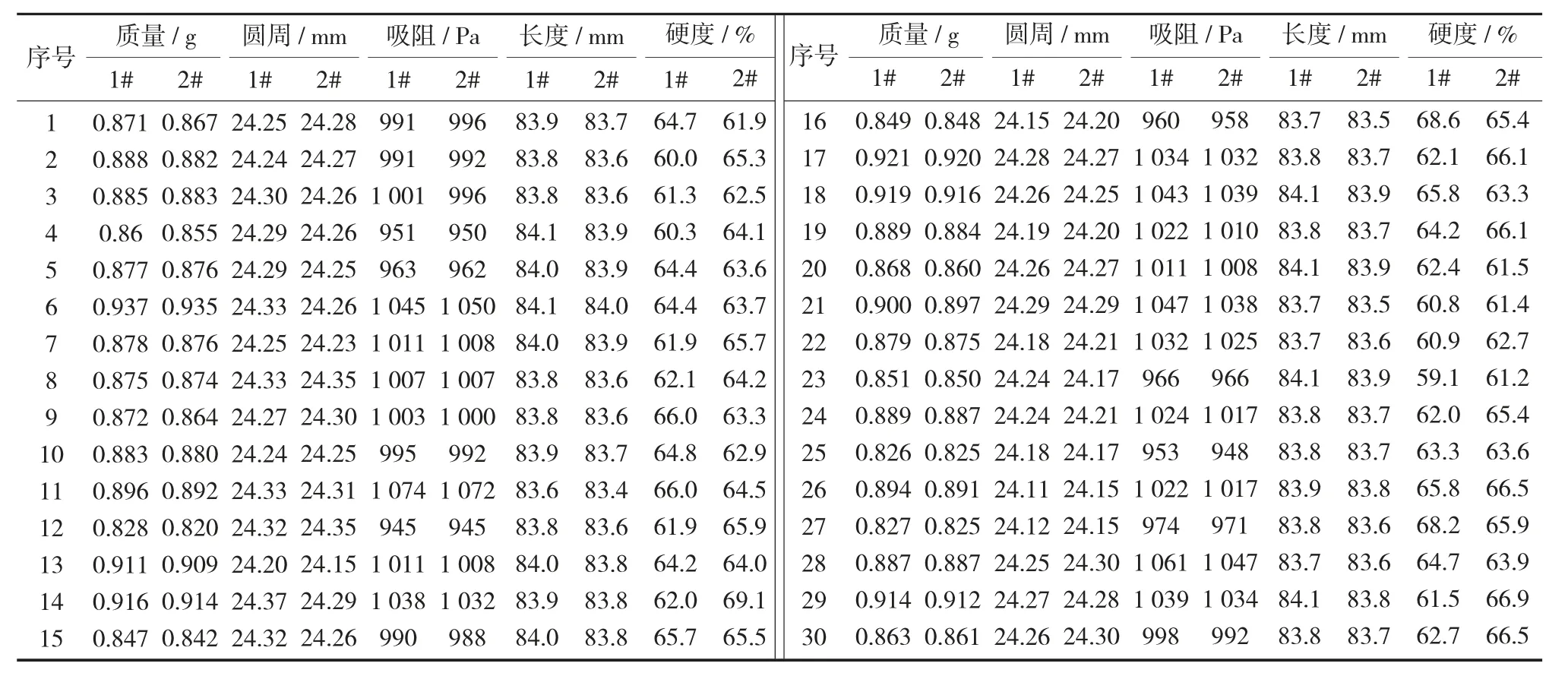
表2 五功能综合测试台测定结果
临界值F0.025(29,29)=0.476、F0.975(29,29)=2.101,显著性水平α=0.05,原假设拒绝域为{F<Fα/2(n-1,m-1)或F>F1-α/2(n-1,m-1)} ={F<0.476 或F>2.101},所有F 统计量0.96,1.29,1.09,1.01,1.62 均未落入拒绝域,因此不能拒绝原假设,故认为1#、2#五功能综合测试台各测量单元测量精密度无显著性差异。
(2) 2 台比对仪器测量结果一致性差异分析。计算1#、2#五功能综合测试台各测量单元测定结果的t 统计量。
2 台五功能综合测试台测定结果t 统计量见表3。
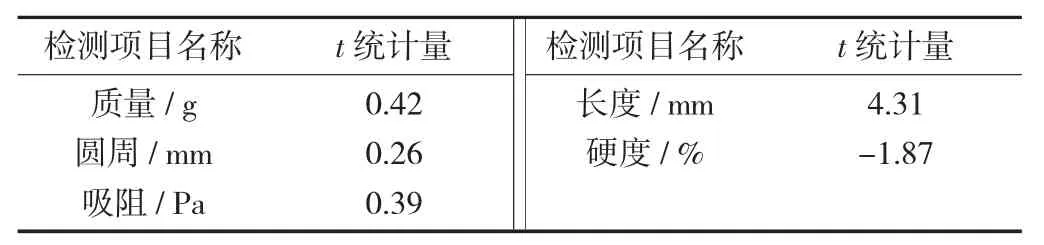
表3 2 台五功能综合测试台测定结果t 统计量
临界值t0.975(58)=2.002,显著性水平α=0.05,原假设拒绝域为{|t|>t1-α/2(n+m-2)}={|t|>2.002},其中长度测量单元t 值为4.31 落在拒绝域中,因此拒绝原假设,认为2#综合测试台长度单元与基准仪器的比对结果有显著性差异,长度单元测量结果的准确性和一致性较差,比对结果不满意,应查找并分析其测量结果出现偏差的原因;质量、圆周、吸阻、硬度测量单元t 值均未落入拒绝域,故认为2#综合测试台质量、圆周、吸阻、硬度测量单元与基准仪器比对结果无显著性差异,测量结果准确性和一致性较好,比对结果满意。
3.2.2 3 台仪器比对结果差异性分析
(1) 3 台仪器比对结果单因素方差分析。3#、4#、5#三功能测试台测量,对其比对结果进行单因素方差分析和多重比较检验。
三功能综合测试台测定结果见表4。
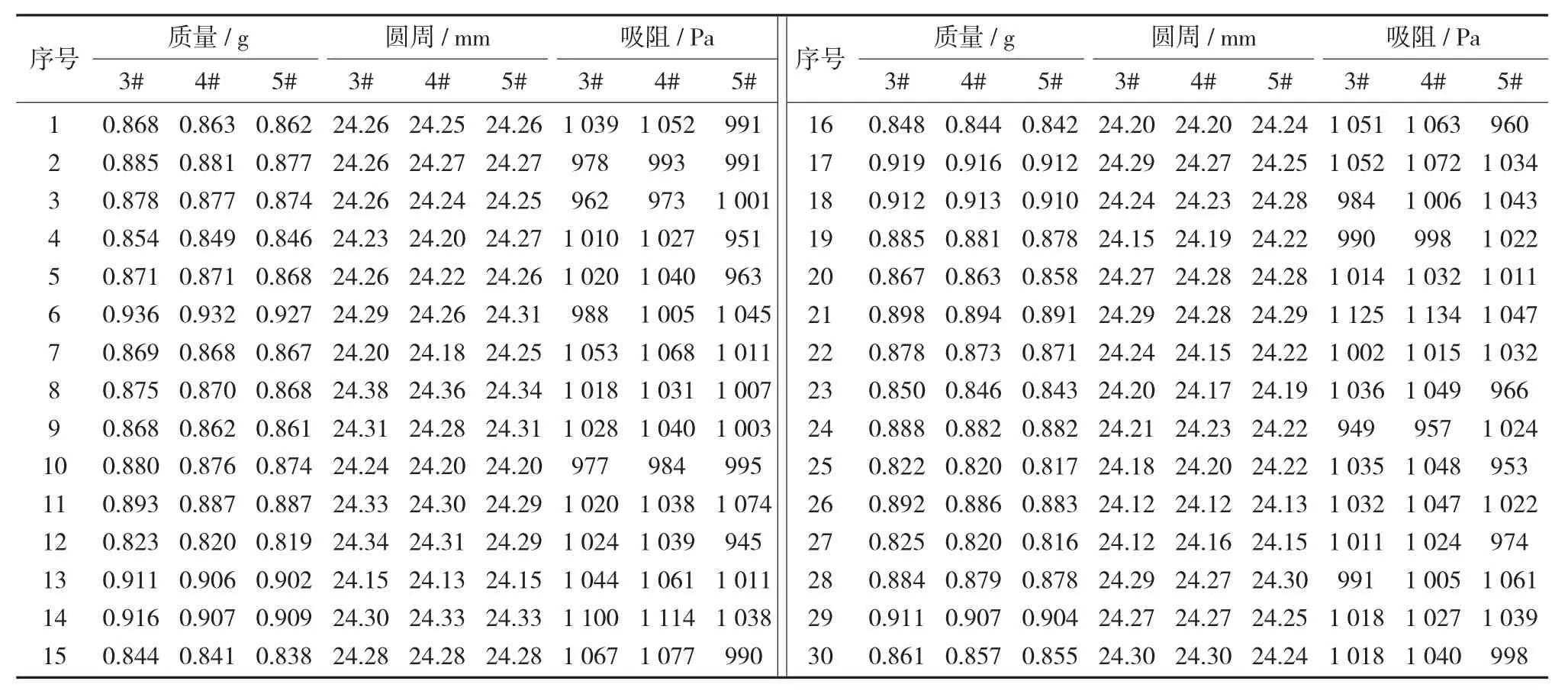
表4 三功能综合测试台测定结果
建立原假设H0:3 台仪器测量数据的均值相同(μ1=μ2=μ3),备择假设H1:参比仪器中至少有一对的均值不同。
显著性水平α=0.05,对3 台三功能测试台不同测量单元测量数据进行单因素方差分析。
三功能测试台质量单元单因素方差分析见表5,三功能测试台圆周单元单因素方差分析见表6,三功能测试台吸阻单元单因素方差分析见表7。
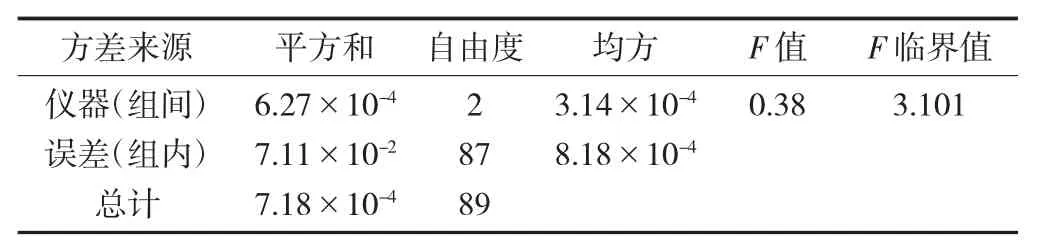
表5 三功能测试台质量单元单因素方差分析
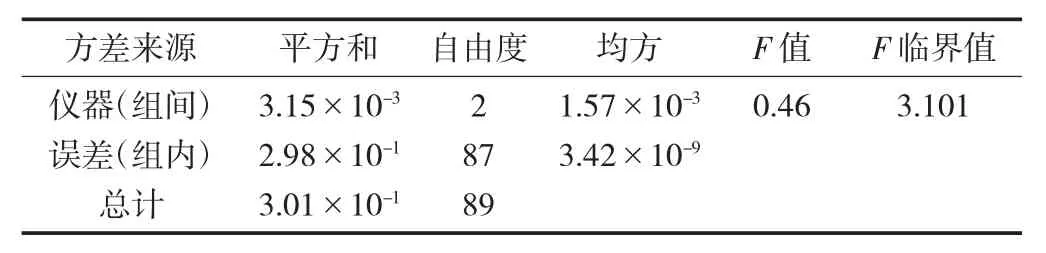
表6 三功能测试台圆周单元单因素方差分析
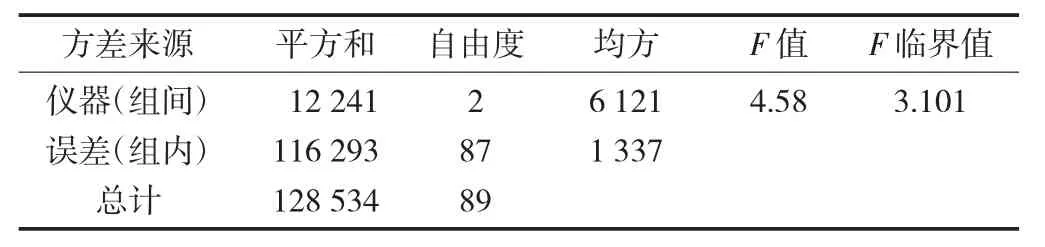
表7 三功能测试台吸阻单元单因素方差分析
临界值F0.95(2,87)=3.101,3 台三功能测试台质量、圆周测量单元F 统计量分别为0.38,0.46,均小于临界值F0.95(2,87),故接受原假设H0,表明3#、4#三功能测试台质量、圆周单元测量结果与基准仪器相比无显著性差异,测量结果的准确性和一致性较好,比对结果满意;3 台三功能测试台吸阻测量单元F 统计量为4.58,大于临界值F0.95(2,87),说明3台三功能测试台吸阻测量单元之间的测量结果存在显著性差异。
(2) 单因素方差分析多重比较法。3 台三功能测试台吸阻测量单元之间的测量结果存在显著性差异,但不确定是每台仪器之间都有显著性差异,还是仅在几台仪器之间存在显著性差异,需通过多重比较检验进一步确定。
通过Minitab 16 软件对3#、4#、5#三功能综合测试台吸阻测量单元测量数据进行Tukey 多重比较。
Tukey 多重比较输出结果见表8。
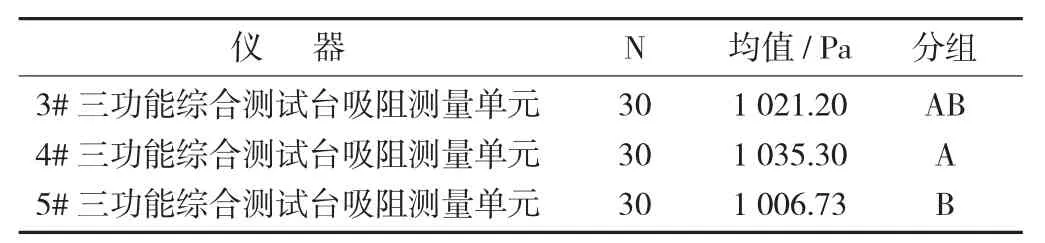
表8 Tukey 多重比较输出结果
由于5#三功能综合测试台为基准仪器,3#综合测试台吸阻测量单元与基准仪器有共享字母“B”,说明两者吸阻测量结果无显著性差异,3#综合测试台吸阻测量单元测量结果的准确性和一致性较好,比对结果满意;而4#综合测试台吸阻测量单元与基准仪器没有共享字母,说明两者吸阻测量结果存在显著性差异,4#综合测试台吸阻测量单元测量结果的准确性和一致性较差,比对结果不满意,应查找并分析4#综合测试台吸阻单元测量结果出现偏差原因,进行纠正改进。
4 结论
详细介绍了卷烟综合测试台比对试验方法及如何进行比对结果分析评价。选定1 台基准仪器,通过比较基准仪器与比对仪器对同一样品的测量结果差异性,评价比对仪器测量结果的准确性和一致性,对于不同数量的参比仪器,应采用不同的假设检验方法进行差异性分析,当参比仪器数量为2 台时,采用F 检验和t 检验进行评价,当参比仪器数量为3台及以上时,采用单因素方差分析和多重比较法进行评价,上述比对方法能科学准确地识别各仪器测量结果的差异性情况,具有简单高效、便于操作的特点,切实有助于生产企业质量控制水平提升和产品质量的稳定。上述比对方法同样适用于卷烟生产线及实验室其他仪器比对。

