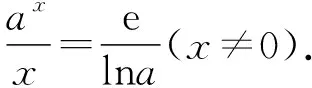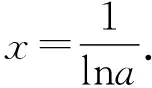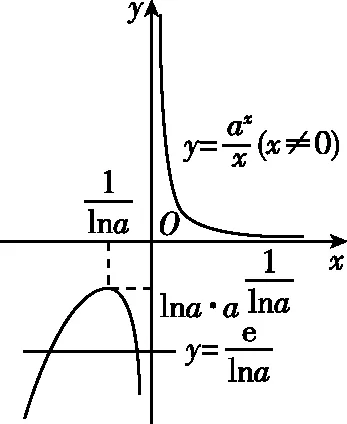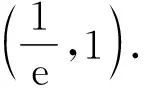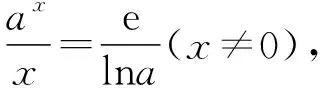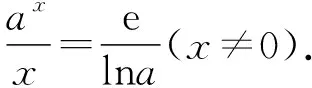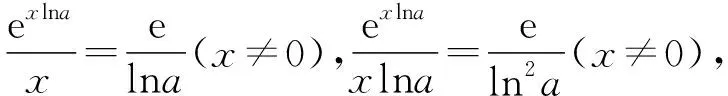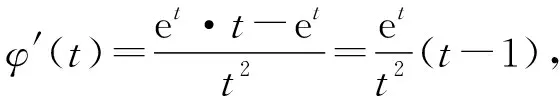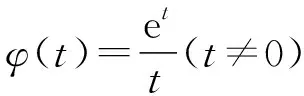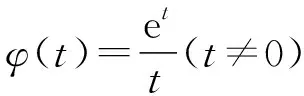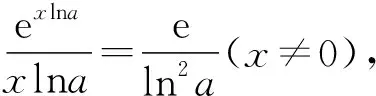运用数形结合 优解函数小题

何红燕

(甘肃省张掖市实验中学)

2022年高考全国乙卷数理第16题是一道考查函数极值、导数等知识的压轴小题,这道题入手容易,深入难,因为它同时考查化归与转化、分类与整合、函数与方程、数形结合等数学思想,深度考查推理论证能力.本文应用等价转化、数形结合、分类讨论等方法破解它,以飨读者.

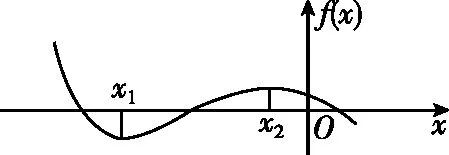
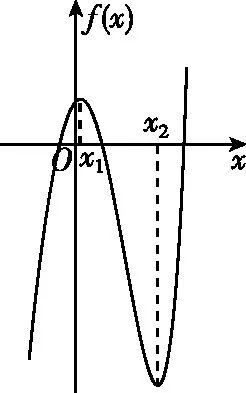
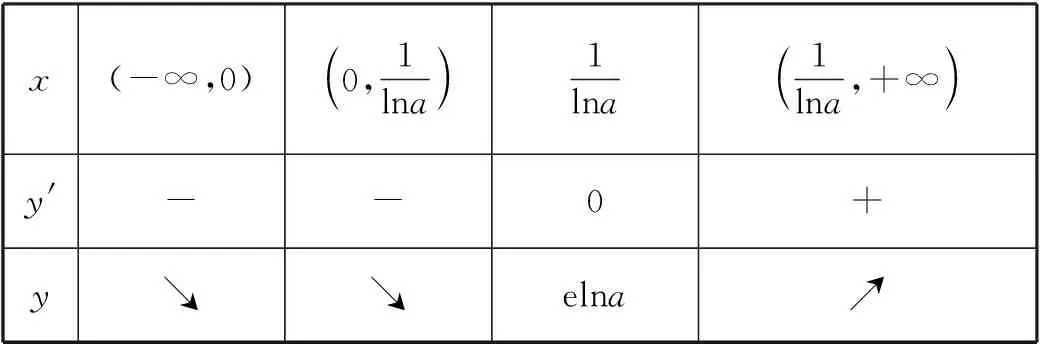
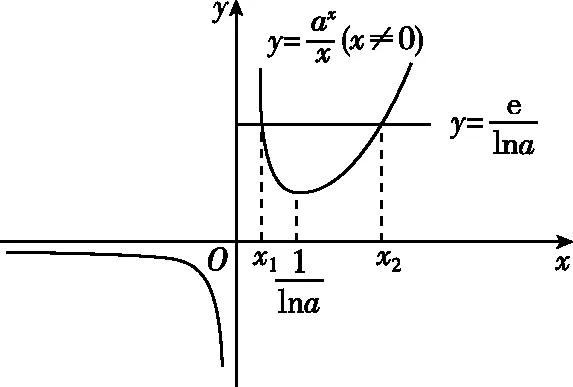
【试题】(2022·全国乙卷(理)·16)已知x=x1和x=x2分别是函数f(x)=2ax-ex2(a>0且a≠1)的极小值点和极大值点.若x1

【分析】本题外表简练朴素,表面考查函数的极值、导数等知识,但内涵丰富,实际考查函数与方程思想、化归与转化思想、分类与整合思想、数形结合思想,试题难度较高,数学素养考查突出,对考生的数学思维水平和推理论证能力都有很高的要求,突出创新性和选拔性,起到很好的区分作用.

【优解1】f′(x)=2axlna-2ex.

因为x1,x2分别是函数f(x)=2ax-ex2的极小值点和极大值点,且x1

所以函数f(x)在(-∞,x1)和(x2,+∞)上单调递减,在(x1,x2)上单调递增,即当x∈(-∞,x1)∪(x2,+∞)时,f′(x)<0,当x∈(x1,x2)时,f′(x)>0,作出函数f(x)和f′(x)的大致图象如图1与图2所示.

图1

图2

(1)若a>1,当x<0时,2axlna>0,2ex<0,则此时f′(x)>0,这与前面矛盾,故a>1不符合题意;

(2)若0

因为0

图3

设过坐标原点且与函数y=axlna的图象相切的直线的切点为(x0,ax0lna),

因为函数y=axlna与函数y=ex的图象有两个不同的交点,

【评注】由方程axlna=ex的两个根为x1,x2,等价转化为函数y=axlna与函数y=ex的图象交点的横坐标为x1,x2,运用了函数与方程的数学思想,再根据图象,数形结合得不等式,解得取值范围,其中数形结合是优化解题的开始,它就像杠杆,撬出了问题的实质.数形结合思想贯穿于整个高中数学,在具体的数学题中,利用数形结合思想解题,将困难的问题转化为容易的问题,将复杂的问题转化为简单的问题,将抽象的问题转化为直观的问题,会达到事半功倍的效果.

【优解2】f′(x)=2axlna-2ex至少有两个变号零点x1和x2,令g(x)=2axlna-2ex,则g′(x)=2ax(lna)2-2e.

(1)若a>1,则g′(x)在R上单调递增,此时若存在x0∈R,使得g′(x0)=0,则f′(x)在(-∞,x0)上单调递减,在(x0,+∞)上单调递增,若f′(x0)<0,此时有x=x1和x=x2分别是函数f(x)=2ax-ex2(a>1)的极大值点和极小值点,g′(x),f′(x),f(x)的大致图象如图4、图5、图6所示,不符合题意.

图4

图5

图6

图7

图8

图9

【评注】(1)含有指对函数、三角函数与多项式函数的方程称为超越方程,一般情况下,高考中函数解答题中f′(x)=0(或g′(x)=0,g′(x)为函数f′(x)的导函数)是超越方程,高中阶段是无法解出超越方程的,此时,我们常用的策略有两种:

①二次求导,即对函数f′(x)再次求导,函数f′(x)的导函数g′(x)的正负对应着f′(x)的增减性,进而得出f′(x)的正负情况,最终确定f(x)的增减情况.

②设而不求,即先分析导函数(或导函数的导函数)的单调性,判断它是否存在零点,若存在,再结合零点存在定理判断零点个数,进而设出零点,对问题进行求解;这里设而不求f′(x)=0与g′(x)=0的根,判断出导数正负的情况,解决函数f(x)的单调性问题.

(2)数形结合有益于解题的顺利进行,能画草图的地方尽量画草图,这里参数a的值不确定,只需要取满足条件的特殊值即可,并不影响结果,a的值越简单方便越有利于解题,往往这样做能起到推动解题、简化解题的良好效果.

【优解3】f′(x)=2axlna-2ex(a>0且a≠1),

因为x1和x2分别是函数f(x)=2ax-ex2的极小值点和极大值点,

图10

(2)当a>1时,若函数g(x)与h(x)的图象有两个不同的交点,则函数的图象如图11所示,当x∈(0,x1)时,f′(x)>0,f(x)在区间(0,x1)上单调递增;当x∈(x1,x2)时,f′(x)<0,f(x)在区间(x1,x2)上单调递减;当x∈(x2,+∞)时,f′(x)>0,f(x)在区间(x2,+∞)上单调递增,则x1为极大值点,x2为极小值点,这与题意不符.

图11

【优解4】f′(x)=2axlna-2ex,

x(-∞,0)0,1lna 1lna1lna,+∞ y'--0+y↘↘elna↗

图12

x-∞,1lna 1lna1lna,0 (0,+∞)y'+0--y↗elna↘↘

图13

(ⅱ)注意逻辑思维的严密性与完整性,二者缺一不可,如上面证明当a>1时,与题意不符的情形.

【优解5】因为f′(x)=2axlna-2ex,

因为ax=elnax=exlna,

t(-∞,0)(0,1)1(1,+∞)φ'(t)--0+φ(t)↘↘e↗

这道题凝聚着命题专家们的心血与智慧,蕴含着丰富的理性精神、数学思想、数学方法.大多数考生看不清问题的本质,想不到解决问题的办法.它起点低、入手难,但更难在与题目的等价转换、灵活运用数学思想方法上.因此,考生解函数题的首要任务是提炼与运用等价转化、数形结合、函数与方程等数学思想方法,所以平时需加强这方面的训练,到考试时,才能如鱼得水、得心应手.另一方面,此题着重考查思维能力与逻辑推理能力,综合考查考生的数学素养水平,暗里强调学习的本质不是把篮子装满,而是如何把灯点亮.

此文为甘肃省教育科学“十三五”规划2019年度《基于数学核心素养的“问题串”引导教学的策略研究》课题(课题批准号GS【2019】GHB0921)阶段性成果之一.