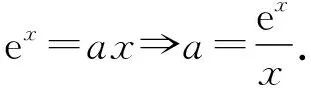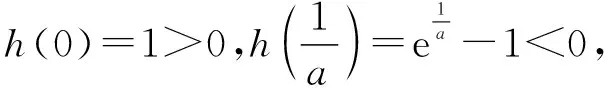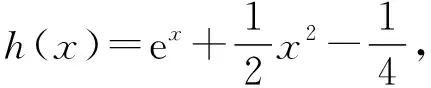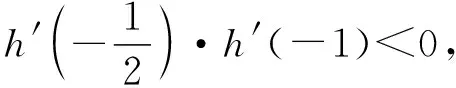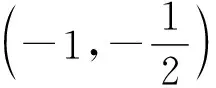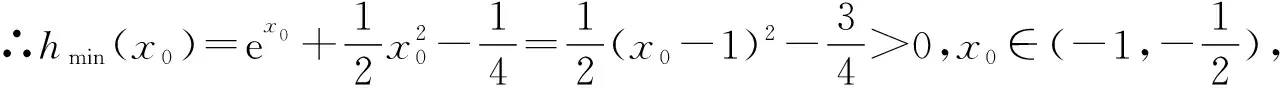深度学习视域下问题设计的“高阶优化”
——以《函数与方程》复习课为例
林迪迪 陈 敏
(浙江省温州市永嘉县罗浮中学)
以《函数与方程》复习课为例,进行深度学习视域下的高三单元复习课的教学实践.首先从低起点的问题引入,带领学生回顾知识的发生、发展的过程,系统化地构建联系,然后再进行螺旋式的变式拓展,帮助学生深化理解核心知识的本质以及所蕴含的数学思想方法,引领学生深度学习,发展理性思维水平,最后通过多维度的探究提炼发展学生的数学素养.
1.问题引领,深度体验
在学生的“最近发展区”设置低起点的典型问题引出课题,能引起学生的共鸣,它是教学的起点,也是思维的增长点,能保证教学过程由浅入深、由表及里、由简单到复杂、由单一到综合、由低到高、循序渐进得开展、促使深度学习.
【引例】函数f(x)=ex-2的零点为________.
生1:ln2.
师:你是如何求得的?
生1:解方程ex=2.
师:厉害!那这道填空题的答案是?
生1:(ln2,0).
其他学生补充:零点是个数,不是个点,不能写坐标,应该是ln2.
师:谢谢你们的解释!这就是我们今天要复习的内容:函数与方程.
师生共同知识总结并板书:
零点的定义:________________.
函数y=f(x)的零点⟺________(函数与方程思想)⟺________(数形结合思想).
【设计意图】通过引例设计,复习了函数零点的定义,从数的角度和形的角度重新认识函数零点.通过创设熟悉的问题情境,唤醒学生已有的知识结构,从数和形的角度认识和感受函数零点、方程的根.
2.螺旋变式,系统构建
深度学习的载体和原动力在于问题的广度、梯度、深度,通过问题变式和方法变式引领学生探究,促进数学知识与方法的迁徙,促使学生的数学思维从低阶逐步跨越到高阶,驱动深度学习的顺利开展.
片段1:合作探究,发现方法
【变式1】判断方程ex-2+x=0的根的个数?并证明你的结论.
教师给出问题,学生小组合作讨论,小组汇报讨论结果.
生2:从形的角度直观判断.ex-2+x=0的根的个数⟺方程ex=2-x的根的个数⟺两个函数f(x)=ex,g(x)=2-x图象交点的个数.将方程的根的个数转换为两个函数图象交点的个数,非常直观的判断方程ex-2+x=0有唯一的根.
师:非常棒!一目了然,一幅图解决了问题.抽象的数的问题转化为直观的形的问题!
生3:令f(x)=ex,则f(x)在R上单调递增.
令g(x)=2-x,则g(x)在R上单调递减.
∵f(0)=1
∴f(x)与g(x)的图象有且只有1个交点,即ex-2+x=0有唯一的根.
师:感谢你!非常不错的想法!但是,这样的想法似乎还缺了点,谁还有补充?
(学生情绪高涨,都在积极思考更加严谨的方法)
生4:从数的角度严格证明.
令f(x)=ex-2+x,
∴f(x)在R上单调递增.
又f(0)=-1<0,f(1)=e-1>0,
∴f(0)·f(1)<0.
由零点存在定理可知f(x)在R上存在唯一的零点,证毕.
师:谢谢你带我们进入严谨的数学世界.方程的根的个数等价于函数零点的个数,然后利用零点存在定理从数的角度严格证明了.非常棒!
师生共同知识总结:
零点存在定理:若函数y=f(x)在区间[a,b]上的图象________,且________,则函数y=f(x)在区间(a,b)上________.
【设计意图】通过变式,加深对函数零点的认识,从数的角度和形的角度来理解函数零点,以及函数与方程之间的转换.
片段2:层层递进,总结方法
【变式2】求函数f(x)=ex,g(x)=ax图象的交点个数?并说明理由.
教师给出问题,学生小组合作讨论,小组汇报讨论结果.
生5:a的几何意义为过原点的直线的斜率.
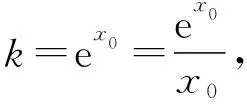
解得x0=1(k为相切时,切线的斜率),
∴切点为(1,e),k=e,
由图可知(图略):
当a>e时,有2个交点;
当a=e,a<0时,有1个交点;
当0≤a 师:厉害,这一小组借助于形,加以数的角度,数形结合判断出交点个数.突破口——发现参数a的几何意义为直线的斜率,反应在形的角度为直线的倾斜程度.那还有其他思考的角度吗? ∴h(x)在(1,+∞)上单调递增,在(-∞,0),(0,1)上单调递减. 根据图象及前面的分析,可得: 当a>e时,有2个交点; 当a=e,a<0时,有1个交点; 当0≤a 师:又是全新的视角,突破口为分离参数a,然后再借助于形的角度解决问题!非常棒,谢谢你的分享! 生7:令h(x)=ex-ax,h′(x)=ex-a, ①当a<0时,h′(x)>0,则h(x)单调递增, ∴h(x)在R上有且只有1个零点. ②当a=0时,没有零点. ③当a>0时,令h′(x)=ex-a>0⟹x>lna, ∴h(x)在(-∞,lna)上单调递减,在(lna,+∞)上单调递增, ∴h(x)min=h(lna)=elna-alna=a(1-lna). 当0 当a=e时,h(x)min=0,∴h(x)有1个零点. 当a>e时,h(0)=1>0,h(x)min=h(lna)<0,h(a)=ea-a2>0. ∴h(x)在(-∞,lna)上有1个零点,在(lna,+∞)上有1个零点,即h(x)在R上有2个零点. 综上所述,当a>e时,有2个零点; 当a=e,a<0时,有1个零点; 当0≤a 师:通过构造函数,借助单调性和零点存在定理对零点情况给予说明.逻辑思维非常的严谨.感谢你! 师:我们刚刚通过三种方法来解决这一问题,我们来总结反思每一种方法.切线法在于找出直线和曲线相切时的特殊情况为出发点,但仅仅适用于凹凸性不变的函数,而且在解答题很难描述清楚,更适用于选择和填空题.参数分离的优点在于避免对参数的讨论,但是会出现分参困难,或者不含参部分难求极值.直接讨论,要对参数进行细致合理的分类,这对学生的能力提出了更高的要求. 【设计意图】通过变式2的铺垫,使学生储备了足够的知识经验,学生自己不断尝试,探索不同的方法,不仅提升了自豪感,而且更加深刻认识了对函数与方程之间的联系、数形结合解决函数零点问题.通过这两道题目,求解思路更宽广,能够整合知识,梳理方法,提升能力,发展核心素养. 3.多维探究,思维进阶 通过上述2个变式的螺旋式探究,学生基本掌握了零点问题的一般求解思路和解答程序,笔者又设置了一道变式,让学生从不同维度探究求解策略,提炼方法,培育理性思维,发展数学素养. 【变式3】已知关于x的函数f(x)=ex-ax2-a2, (Ⅰ)当0 教师给出问题,学生小组合作讨论,小组汇报讨论结果. 生8: (Ⅰ)f′(x)=ex-2ax,令q(x)=f′(x),则q′(x)=ex-2a, 令q′(x)>0⟹x>ln2a, 所以f′(x)在(ln2a,+∞)上单调递增, 在(-∞,ln2a)上单调递减. ∴[f′(x)]min=f′(ln2a)=eln2a-2aln2a=2a(1-ln2a)>0, ∴f′(x)恒为正. ∴f(x)在R上单调递增. 又f(0)=1-a2>0,f(lna2)=-a(2lna)2<0, ∴f(0)·f(lna2)<0. 由零点存在定理可知,f(x)在R上有唯一的零点. 师:非常厉害!完美诠释了数学严谨! 生9:(Ⅱ)解法1: 令g(a)=-a2-x2a+ex, (3)式显然成立. 下面先证(1)式. ∴h′(x)在R上单调递增. 同理可证(2)式成立. 解法2: 先证(1)式. 由切线不等式ex≥x+1(当且仅当x=0时等号成立),可得 下证(2)式: 由切线不等式ex≥x+1可得 师:今天主要讲解函数零点的相关问题.由于时间关系,这道题留给同学们自己课后思考,还可以从其他哪些角度思考. 以上问题,学生主动探究,自主构建,互动交流,课堂十分活跃,同学们收获满满,教学效果令人满意. 4.教学反思及感悟 基于核心素养的深度学习,不同于传统的被动接受,在课堂教学过程中以问题为载体,以自主探究和高阶思维为学习与解决问题的基本手段,获得对知识方法、思维方式的深度理解与建构.既是一种指向核心素养、利于核心素养生成的学习,也是一种追求知识的“质”胜过追求知识的“量”的学习. 4.1 数学课堂应给足学生“悟”的时间——深层体验 本节课采用学生小组讨论、小组汇报的形式进行,课堂是在学生的思维活动中构建的.在教学过程中要充分相信学生,让学生全面、深入地参与教学过程.学之道在于“悟”.数学学习的本身就需要有悟的过程,悟的过程就是一个自我思考、自我反思、自我总结的过程.通过小组讨论中思维的碰撞、以及自我反思总结,对学习对象蕴含的数学本质、规律进行思考和做出判断,不断地提高学生的数学思维品质.让核心素养渗透到每一个教学环节中,流淌于各个不同的数学知识之间.在学生深层体验中亲历解题过程,感悟解题思想方法,内化知识,构建自身知识体系,发展核心素养. 4.2 数学课堂恰当选择“最近发展区”——深入探究 维果斯基提出“最近发展区”理论,教师的职责在于引导、帮助学生从已有的水平发展到他可能达到的水平.在实际课堂上,如何寻觅学生的“最近发展区”?如何选择最佳的“教学最佳区”?“最近发展区”可能是知识型、方法型、能力型,还是可以是素养型,因此在课堂教学过程中,应当综合考量、具体分析,辩证思考,从中选择最适合学生的最佳“最近发展区”实施教学.比如在变式2的教学中,学生在平时学习中已经非常熟悉此类问题,积累了多种教学方法,直接讨论法最易想到,但是参数的变化对函数单调性的影响,需要学生对此进行细致的分类讨论.教师需要在学生的原有基础上,进行有方向的引导教学. 4.3 强化思考交流,培养高阶思维——深化思考 问题和变式在教学过程中起到很好的驱动作用,教师引导学生剖析问题本质,从“变”的现象中发现“不变”的方法本质,总结通性通法,然后再从“不变”的本质中探索“变”的规律,体现知识的迁移,为学生搭建解决问题的台阶.深度视域下的复习课还要以拓展和延伸为突破口,变换不同的问题情境,促进学生多维度深度思考,最终实现对知识体系和思想方法的感悟和内化,培养学生的高阶思维,提升学生的核心素养. 我们应该关注每个教学环节,从每一个教学设计做起,立足每一个知识、方法,进行深度教学,让学生进行深度学习,那么学生的数学能力的培养和数学核心素养的发展就不是一句空话,就能够在课堂教学过程中落地生根、开花结果,促进学生终身发展.