融合相空间重构和深度学习的径流模拟预测
师鹏飞 赵酉键 徐辉荣 李振亚 杨涛 冯仲恺

摘要:发展对数据依赖程度低、快捷实用和精准的模拟预报技术,可为资料缺乏地区径流模拟预测提供有效的解决办法。从数据驱动的角度,提出一种融合相空间重构(PSR)和长短期记忆神经网络(LSTM)的径流预测复合模型PSR-LSTM,在国内外不同气候分区的10个流域(站点)进行验证。结果表明:PSR-LSTM能够提取水文变量的多维子空间特征,并较好预测不同时间尺度的径流变化过程;相较于LSTM,PSR-LSTM预测未来1、3、5、7、9时间步长的纳什效率系数在10个流域平均提高1.49%~9.77%,均方根误差平均降低17.01%~19.72%,对训练数据量的依赖程度相比LSTM降低25%~33%。研究成果可为广大资料短缺流域水文过程模拟和预测提供参考。
关键词:径流预测;数据驱动;人工智能;相空间重构(PSR);长短期记忆神经网络(LSTM)
中图分类号:TV122
文献标志码:A
文章编号:1001-6791(2023)03-0388-10
收稿日期:2022-11-22;
网络出版日期:2023-05-23
网络出版地址:https:∥kns.cnki.net/kcms2/detail/32.1309.P.20230522.1828.002.html
基金项目:国家自然科学基金资助项目(52279009);中央高校基本科研业务费专项经费资助项目(B220201010)
作者简介:师鹏飞(1987—),男,副教授,博士,主要從事流域水文物理规律模拟及水文预报方面研究。
E-mail:pfshi@hhu.edu.cn
水文预警预报对防洪减灾至关重要,受资料条件和科技水平等制约,在监测资料不足的河流,传统水文模型往往无法建立[1]。近年来,受气候变化和高强度人类活动共同影响,极端水文事件发生频次及量级远超历史,流域安全风险问题更加突出。2021年郑州“7·20”洪涝灾害再次凸显及时预警预报的重要性[2]。因此,创新水文预报的技术和方法,发展对数据依赖程度低、快捷实用和精准的模拟预报技术,对于难以建模的资料缺乏地区具有重要的科学和现实意义。
基于物理过程的水文模型是常用的径流模拟预测方法,由于建立物理过程模型所需的降水、径流、蒸散发、流域特性、断面形状、闸阀工况等数据往往难以全部获取,水文过程建模常存在难度[3],在资料稀缺的中小河流域尤为突出。另一方面,数据驱动的模拟预测技术正在经历空前的快速发展。国际上,Ham等[4]研究表明,数据驱动的人工智能(AI)模型用于模拟预测ENSO,相比经典动力学模型,纳什效率系数提升显著;Ravuri等[5]研究表明,以人工神经网络为代表的机器学习方法,利用历史气象水文时间序列数据即可对洪水进行模拟和实时预测,能够模拟复杂的非线性水文过程,具有精度高、时效性强等优点。大量研究表明,数据驱动的预报方法不失为一种有效途径。
长短期记忆神经网络(LSTM)作为一种先进、稳定的深度学习算法,被广泛应用在时间序列预测中[6]。然而,直接将水文时间序列作为输入,驱动LSTM进行预测,由于缺乏对水文多维特征复杂信息的挖掘与表征,存在易过度拟合、对训练样本量依赖程度高、精度不足等问题[7],限制了模拟预测效能,特别是在资料短缺流域。如何全面挖掘水文数据中蕴含的水文系统变化规律,提高深度学习算法的径流模拟预测效能,有待深入探究。
针对上述问题,本研究引入动力系统理论,考虑水文序列的混沌特性,提出基于相空间重构(PSR)的水文变量相空间特征自适应快速挖掘和重建技术,建立基于PSR-LSTM复合模型的数据驱动模拟技术框架,在国内外不同气候分区的多个流域进行应用验证,以期提升数据驱动模型的模拟预测效能,为资料缺乏地区径流模拟预测提供便捷、有效的方法工具。
1 相空间重构和长短期记忆神经网络方法
1.1 相空间重构方法
相空间重构理论最早由Takens等[8]提出,其目的为在高维相空间中重建混沌吸引子。混沌吸引子作为混沌系统的特征之一,体现着混沌系统的规律性(图1)。决定系统长期演化任一变量的时间序列,均包含了系统所有变量长期演化信息,因此可由已知的时间序列,恢复并重建原动力系统。
研究表明,水文序列可视为混沌系统[9],对于某一时间序列X=[x1,x2,x3,…,xN],在估计出恰当的嵌入维数(m)和延迟时间()后,可以重构相空间,形成N-(m-1)个m维向量:
式中:N为时间序列长度;M为项点数,M=N-(m-1)。
1.2 最大Lyapunov指数
通过最大Lyapunov指数(λ>0)可以判断时间序列是否具有混沌特性,目前已经广泛应用在混沌判别和混沌时间序列预测领域中。最大Lyapunov指数可由Wolf法求解[10]。Wolf法求解最大Lyapunov指数的计算公式为
1.3 长短期记忆神经网络
以LSTM、循环神经网络(recurrent neural network,RNN)为代表的深度学习算法,因强大的自适应和自学习能力,近年来被广泛应用于电力系统的电力负荷和气象水文要素的预测预报中[11-12]。LSTM通过增加门控机制来控制历史时刻对当前时刻的影响程度,从而解决了RNN容易产生梯度弥散和梯度爆炸的问题。详细介绍可见文献[13]。
2 PSR-LSTM复合模型构建
2.1 建模流程
资料匮乏地区用于建模的水文变量种类单一、样本短缺,难以构建概念性或物理过程模型。采用数据驱动模型也面临因特征变量少而陷入过拟合或泛化能力不足的问题。针对此,本研究充分挖掘PSR在相空间特征自适应挖掘与重建方面的优势及LSTM在非线性时间序列预测方面的优势,将水文变量信息投映到高维空间中,将重构后的特征向量作为LSTM的特征变量进行建模,构建PSR-LSTM复合模型,以实现快速高效建模,减少数据依赖的同时、提高模拟预测精度。PSR-LSTM模型分析计算流程如下:
(1) 数据准备。水文过程建模常用数据一般包括降水、蒸散发、流量、水位等时间序列数据(逐日或逐小时)以及下垫面空间数据(DEM、地貌、植被覆盖、水系、土壤类型、土壤厚度等)。考虑水文预报预测快捷建模的需求,结合当前多数中小流域资料短缺的客观实际,本研究仅选取流域中最为常见的水位或流量时间序列用于建模。数据前80%作為模型训练集,后20%作为测试集。
(2) 相空间重构。考虑仅有径流(水位或流量)数据,属水文“小数据”,为充分挖掘数据中包含的复杂信息,尽可能全面地考虑水文变量中蕴含的系统规律,采用PSR方法对径流数据进行挖掘分析,获取径流时间序列中蕴含的多维子特征,将一维数据映射到多维相空间中。
(3) 数据标准化。对重构后的多维矩阵序列进行归一化处理,范围控制在0~1之间。
(4) 预测模型构建。搭建LSTM模型,将基于PSR重构后的每一维特征向量作为LSTM的时间步长输入网络,根据PSR中求取的嵌入维数确定LSTM输入层节点数。按批构造实测径流数据,调整超参数确定神经网络的深度,采用Adam优化算法求得模型相对最优解,并在各层之间采用Dropout技术避免模型出现过拟合情况,最后通过反归一化处理得到模型预测值。
(5) 模型效能评价。采用纳什效率系数、均方根误差、洪峰相对误差、峰现时间误差等指标进行精度评价,评估模型效能。
2.2 情景模拟分析
为分析评估PSR-LSTM模型效能,设置S1、S2、S3、S4和S5共5种情景(表1),其中,S1、S2为利用重构后的水文变量进行PSR-LSTM建模的情景,分别采用中等和较少数据量;S3、S4和S5为利用原始水文变量进行LSTM建模的情景,分别采用中等、较少和较多数据量。较多数据量指采用尽可能长的水文时间序列(即表2中序列长度),中等数据量约取较多数据量的80%,较少数据量取60%,通过递减数据量,分析模型训练对数据的依赖程度。通过几种情景的对比分析,阐述PSR-LSTM和LSTM模型的预测精度、预见期及对数据依赖程度的异同。
2.3 模型效能评价指标
采用纳什效率系数(ENS)、均方根误差(ERMS)、洪峰相对误差(EPF)和峰现时间误差对模型效能进行评价,公式如下:
式中:Qs(j)为模拟预测值;Qo(j)为实测值;Qo为实测值的平均值;Qsp和Qop分别为模拟和实测洪峰值。ENS越大、ERMS越小,表示模拟精度越高,ENS取值最大为1。按照水文情报预报规范要求[14],采用洪峰相对误差、峰现时间误差对逐小时尺度的模拟预测结果进行评价,对逐日模拟预测值不予评价。
3 实例分析
3.1 研究区及数据介绍
为充分验证模型的鲁棒性,考虑不同气候分区下流域水文规律的差异性,选取了涵盖中国和澳大利亚湿润区、半湿润半干旱区和干旱区共10个流域(站点)进行模型应用验证。其中,中国流域数据均来自当地水文局(中心)整编数据,澳大利亚数据来自CSIRO建模者数据集[15],数据可靠性高。数据时间尺度为逐日或逐小时,有多次水位/流量上涨过程,具有代表性。详见表2。
3.2 相空间重构参数估计
相空间重构的关键在于估计合适的嵌入维数和延迟时间。Kim等[16]提出的基于时间窗口的C-C法被广泛应用,本文采用C-C法估计相空间重构的参数,详见文献[16]。利用Wolf法计算的最大Lyapunov指数均大于0,表明径流系列均具备混沌特性,参数估计结果见表3。
3.3 PSR-LSTM模型训练及参数设置
按照预见期分别为1、3、5、7、9个时间步长进行建模。建模前,对输入数据进行归一化处理,采用Adam(梯度下降法)作为模型优化器,选择EMS作为代价函数,检验模型预测值和真实值之间的偏差,EMS公式如下:
式中:EMS为均方误差;Yi为真实值;Y^i为模型预测值。
滑窗长度、滑窗数均为深度学习模型的超参数,据此可将数据按批次放入模型中训练。通常将参数设置为2的倍数,可较好符合计算机硬件尺寸阵列(如计算机内存单元为210),提升训练效率。基于试错法,将滑窗长度设置为16,每批数据包含128个滑窗。
3.4 模拟结果与分析
3.4.1 PSR-LSTM与LSTM对比
考虑到在实际应用中,往往较难获取完整的水文时间序列数据。故本文选择中等样本数据量进行模型训练,通过对比PSR-LSTM和LSTM模型在S1、S3情况下的模拟结果,验证PSR-LSTM的模型性能。
图2所示为PSR-LSTM和LSTM模型在10个流域(站点)模拟效能的纳什效率系数。随着预见期的增加,2个模型的ENS均呈下降趋势,而PSR-LSTM下降过程更平缓,箱体变化范围PSR-LSTM较LSTM更小,表明在不同流域的离散程度更低。箱体上延线、下延线及内部中位数横线均较LSTM更高,特别是5步长以后,模型效能更优。在大部分流域的模拟预测中,PSR-LSTM模型预测精度优于LSTM模型,不同预见期下的ENS中位数(箱图中值线)在10个流域平均提升1.49%~9.77%,ERMS平均降低17.01%~19.72%,详见表4。
如表5所示,PSR-LSTM预测未来1、3、5、7时间步长的EPF大部分在许可误差(峰值的20%)内,三门峡站从5步长以后预测均超出许可误差,干旱区、半湿润半干旱区站点的9步长预测相对误差超出许可误差。整体而言,PSR-LSTM在9个时间步长的EPF平均值,不同流域下较LSTM平均降低0.49%~8.93%。在逐小时模拟预测(信宜、三都站)的峰现时间方面,PSR-LSTM相比LSTM结果相近,但在三都站的3个步长和5个步长预测中,峰现时间均有1 h的提升,其他步长的结果一致。
3.4.2 PSR-LSTM与LSTM模型对训练数据量的依赖程度
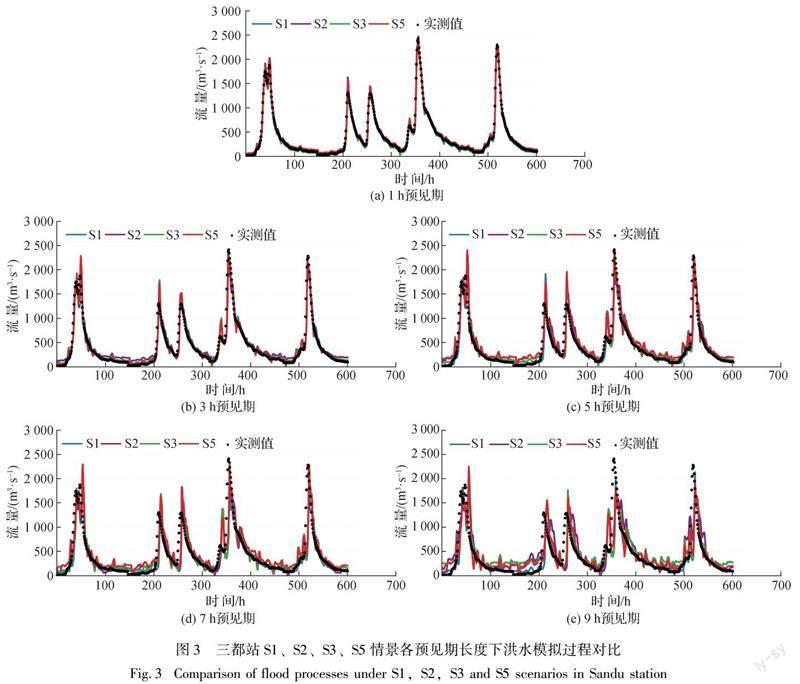
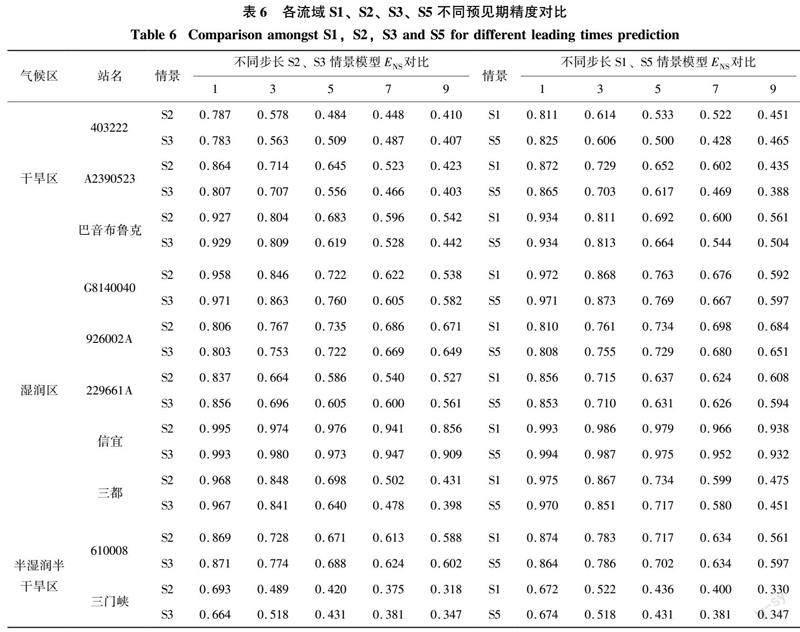
通过对比S1、S2、S3、S5等4种建模情景,分析模型对训练数据量的依赖程度,结果见表6和图3。
表6展示了在不同预见期下,各流域S1、S2、S3和S5情景的ENS系数对比。结果表明:① S1和S5在湿润区、半湿润半干旱区精度相似,在干旱区3个步长以后,S1的预测精度均优于S5,即PSR-LSTM在中等样本量下的效能优于较多样本量下的LSTM。② S2在部分流域优于S3,在部分流域劣于S3,总体精度基本相当,可认为PSR-LSTM在小样本量下与LSTM在中等样本量下的效能相似。总体而言,从10个流域采用的数据量来看,在相似精度条件下,PSR-LSTM对训练样本的依赖程度较LSTM更低,平均降低约25%~33%。
为展示模拟预报过程,受限于篇幅长度,仅选择三都站作为代表,绘制了各情景下不同预见期长度的洪水模拟预报过程(小时尺度),见图3(图示为验证期结果,20%的数据长度)。可以看出:模型在1~7 h预见期时对洪峰预测均取得良好效果,在低流量过程情况时预测值偏高,模型预测实际偏安全,满足洪水预报要求。对比各预见期不同情景下的洪水预测过程,1~7 h中等数据量PSR-LSTM(S1)与较多数据量LSTM(S5)的预测效果相似,在9 h预见期PSR-LSTM(S1)预测更优。洪峰预测和低流量预测中较少数据量PSR-LSTM(S2)效果与中等数据量LSTM(S3)基本相当,表明数据量减少情况下,PSR-LSTM模型仍能保持预测效果的稳定。
4 结 论
为对资料短缺流域的水文过程进行快捷实用的建模及预测,本文提出了一种融合相空间重构和长短期记忆神经网络的径流预测复合模型PSR-LSTM,建立了包括数据准备、相空间重构、数据标准化、预测模型构建、模型效能评价等步骤的数据驱动建模框架,并将模型在10个不同气候分区流域(站点)进行了应用验证,结论如下:
(1) 得益于PSR挖掘径流数据中的多维复杂信息,PSR-LSTM模型较LSTM模型具有更高的预测精度。预测未来1、3、5、7、9时间步长的ENS在10个流域平均提高1.49%~9.77%,个别流域在长预见期时最高可达29.18%,均方根误差平均降低17.01%~19.72%,峰值误差平均降低0.49%~8.93%。在逐小时预测的峰现时间误差方面,PSR-LSTM较LSTM有少量降低。
(2) PSR考虑了水文数据中蕴含的系统变化规律,通过挖掘多维子空间特征,有助于减少对历史数据量的依赖程度。PSR-LSTM利用较少样本量建模可达到LSTM利用中等样本量的效能,利用中等样本可优于LSTM利用较多样本的效能,建模所需数据量较LSTM减少25%~33%。表明PSR-LSTM模型更适用于样本短缺的流域,对数据缺乏地区的水文预报工作具有参考意义。
(3) 整体而言,在国内外不同气候分區的10个流域(站点)的模拟结果表明,PSR-LSTM能够较好捕捉不同流域水文过程变化规律,具有良好的适用性和鲁棒性。
需指出的是,本文仅从水文变量自相关角度进行建模,分析了PSR-LSTM相较LSTM的提升效果,一方面为验证PSR的作用,另一方面旨在为无资料或缺资料流域提供参考方法,因此长预见期时,不可避免出现纳什效率系数精度不高的问题。在实际应用时,可通过增加和调整特征变量(预报因子)进行建模,以达到更佳效果。由于通常需要利用多种水文变量进行建模预报,后续将研究多变量相空间重构法,对多种水文变量(比如增加降雨、前期影响雨量、蒸散发等)进行相空间重构,最大程度提取水文变量蕴含的复杂信息,以进一步提高模型的预测能力。
参考文献:
[1]雍斌,张建云,王国庆.黄河源区水文预报的关键科学问题[J].水科学进展,2023,34(2):159-171.(YONG B,ZHANG J Y,WANG G Q.Key scientific issues of hydrological forecast in the headwater area of Yellow River[J].Advances in Water Science,2023,34(2):159-171.(in Chinese))
[2]杨宇涵,殷杰,王丹丹,等.基于ABM的城市暴雨洪涝灾害应急疏散仿真研究:以河南郑州“7·20”特大暴雨洪涝灾害为例[J].中国科学:地球科学,2023,53(2):267-276.(YANG Y H,YIN J,WANG D D,et al.ABM-based emergency evacuation modelling during urban pluvial floods:a “7·20” pluvial flood event study in Zhengzhou,Henan Province[J].Scientia Sinica Terrae,2023,53(2):267-276.(in Chinese))
[3]雷晓辉,王浩,廖卫红,等.变化环境下气象水文预报研究进展[J].水利学报,2018,49(1):9-18.(LEI X H,WANG H,LIAO W H,et al.Advances in hydro-meteorological forecast under changing environment[J].Journal of Hydraulic Engineering,2018,49(1):9-18.(in Chinese))
[4]HAM Y G,KIM J H,LUO J J.Deep learning for multi-year ENSO forecasts[J].Nature,2019,573(7775):568-572.
[5]RAVURI S,LENC K,WILLSON M,et al.Skillful precipitation nowcasting using deep generative models of radar[EB/OL].2021:arXiv:2104.00954.https:∥arxiv.org/abs/2104.00954.
[6]李大洋,姚轶,梁忠民,等.基于变分贝叶斯深度学习的水文概率预报方法[J].水科学进展,2023,34(1):33-41.(LI D Y,YAO Y,LIANG Z M,et al.Hydrologic probabilistic prediction method based on variational Bayes deep learning[J].Advances in Water Science,2023,34(1):33-41.(in Chinese))
[7]SKOULIKARIS C,ANAGNOSTOPOULOU C,LAZOGLOU G.Hydrological modeling response to climate model spatial analysis of a south eastern Europe international basin[J].Climate,2019,8(1):1-17.
[8]TAKENS F.Detecting strange attractors in turbulence[J].Lecture Notes in Mathematics,1981,898:366-381.
[9]李禄德,崔东文.基于小波包分解与相空间重构的SSA-ELM水文时间序列预报模型[J].人民珠江,2022,43(8):100-108.(LI L D,CUI D W.SSA-ELM hydrological time series forecast model based on wavelet packet decomposition and phase space reconstruction[J].Pearl River,2022,43(8):100-108.(in Chinese))
[10]NEPOMUCENO E G,MARTINS S A M,LACERDA M J,et al.On the use of interval extensions to estimate the largest Lyapunov exponent from chaotic data[J].Mathematical Problems in Engineering,2018,2018:1-8.
[11]王欣然,馮磊华,杨锋,等.基于PSR-LSTM的机组负荷短期预测研究[J].热能动力工程,2021,36(5):66-72.(WANG X R,FENG L H,YANG F,et al.Study on short-term load forecasting of units based on PSR-LSTM[J].Journal of Engineering for Thermal Energy and Power,2021,36(5):66-72.(in Chinese))
[12]李步,田富强,李钰坤,等.融合气象要素时空特征的深度学习水文模型[J].水科学进展,2022,33(6):904-913.(LI B,TIAN F Q,LI Y K,et al.Development of a spatiotemporal deep-learning-based hydrological model[J].Advances in Water Science,2022,33(6):904-913.(in Chinese))
[13]BULUT M.Hydroelectric generation forecasting with long short term memory (LSTM) based deep learning model for turkey[EB/OL].2021:arXiv:2109.09013.https:∥arxiv.org/abs/2109.09013.
[14]水文情报预报规范:GB/T 22482—2008[S].北京:中国标准出版社,2009.(Standard for hydrological information and hydrological forecasting:GB/T 22482—2008[S].Beijing:Standards Press of China,2009.(in Chinese))
[15]ZHANG Y Q,VINEY N,FROST A,et al.Collation of Australian modeller′s streamflow dataset for 780 unregulated Australian catchments[R].ACT:CSIRO,2013:115.
[16]KIM H S,EYKHOLT R,SALAS J.Nonlinear dynamics,delay times,and embedding windows[J].Physica D:Nonlinear Phenomena,1999,127(1/2):48-60.
Abstract:Developing low data-dependent,efficient,practical and accurate modeling techniques can provide effective solutions for hydrological simulation and prediction in areas with limited data availability.From a data-driven perspective,a composite streamflow prediction model,PSR-LSTM,which integrates Phase Space Reconstruction (PSR) and Long Short-Term Memory (LSTM) networks,was proposed in this study and validated globally over ten river basins (stations) in different climate zones.The results indicate that the PSR-LSTM can effectively extract multi-dimensional sub-space hydrological features and accurately predict streamflow changes at different time scales.Compared to LSTM,the Nash efficiency coefficient of PSR-LSTM in predictions of future 1 to 9 timesteps is increased by an average of 1.49% to 9.77% over the ten river basins;the root mean square error is reduced by an average of 17.01% to 19.72%.The dependency on the amount of training data is reduced by 25% to 33% for PSR-LSTM compared to LSTM.The research findings obtained in this study provide insights into hydrological simulation and prediction in data-scarce river basins.
Key words:streamflow prediction;data-driven;artificial intelligence;Phase Space Reconstruction (PSR);Long Short-Term Memory (LSTM) networks

