基于趋势拟合法、平滑法和ARIMA 模型的流量预测

马政达（中国联通研究院，北京 100048）

1 研究背景

随着宽带用户网络需求的快速增长和固网数据的大幅提升，运营商越来越重视宽带用户的使用体验，并投入更多的精力用于固网宽带网络设备的扩容和维护［1−2］，科学规划网络容量已成为运营商发展的重要议题。网络流量指标是评价网络管理质量的重要参数，对流量的预测是指依据设备历史数据对未来一段时间的流量进行建模与估计，相较于流量达到告警阈值后再升级设备，流量预测可以帮助网络管理员掌握网络变化的规律，更合理地安排预算、设备升级和割接计划，也极大地改善了用户上网体验。此外，随着运营商算力的提升，流量预测甚至可以应用到用户级别，为提供个性化服务做支撑，因此流量预测一直是网络研究领域的重要研究方向［3−5］。

通常当OLT 上联口的宽带利用率峰值到达70%时就需要开始考虑流量扩容［6］，同时用户的下行网络流量往往要高于上行网络流量，因此对OLT 上联口的下行流量速率峰值进行时间序列的分析、预测具有重要意义，是OLT扩容的主要技术指标。

宽带设备的流量速率是网管系统记录的主要数据之一，OLT 下行流量速率峰值数据可以看做是一组时间序列，对于时间序列的分析主要包括模型识别、模型拟合、模型诊断3个步骤［7］。

在模型识别阶段需要根据时间序列的时序图特征和统计量特征选择合适的模型。时间序列的统计学模型有很多，包括趋势拟合法、平滑法及ARIMA 等模型。运营商积累了大量流量数据，但对这类数据的处理往往比较粗犷，经常使用到的流量预测方法有线性拟合法和移动平均法，这些方法操作简单，模型直观，但也存在拟合度低、预测效果差的缺点［8］。相比而言，Holt−Winters 模型和ARIMA 模型增加了更复杂的模型维度和参数类别，可以更充分地拟合复杂的流量趋势及短期的随机趋势。

2 建模及预测

选取一台典型的OLT 的上联口，将其周末的下行速率峰值数据（以下简称流量数据）作为研究对象，时间跨度为2018年9月到2019年5月，共33周。将前30周数据作为训练集，后3 周数据作为测试集。图1 所示为流量数据训练集的时序图、自相关系数图（ACF）和偏自相关系数图（PACF）。

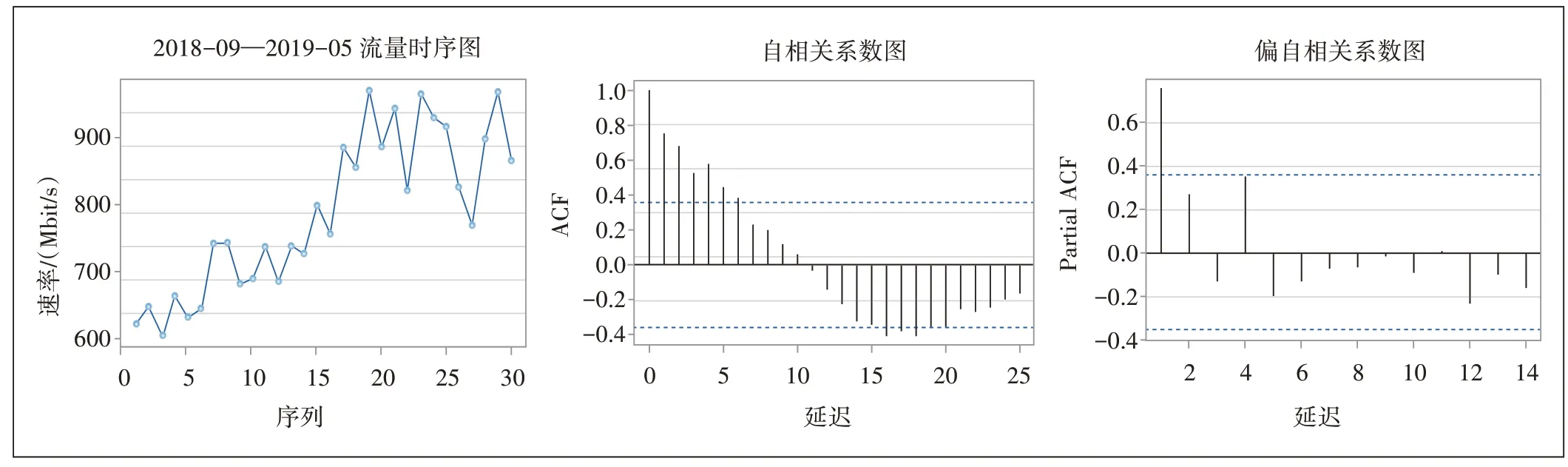
图1 流量数据训练集的时序图和相关性分析

2.1 趋势拟合法

趋势拟合法就是将时间作为自变量，对应的流量观察值作为因变量，建立序列值随时间变化的回归模型的方法。依据观察值的时序图，如果时序图中序列表现出线性的长期趋势，可以考虑使用线性拟合；如果长期趋势呈现出非线性特征，则可以尝试使用曲线拟合［9］。

从图1的流量时序图中可以看出流量趋势平稳上升，呈现出线性趋势，因此进行线性拟合，结果如图2所示。

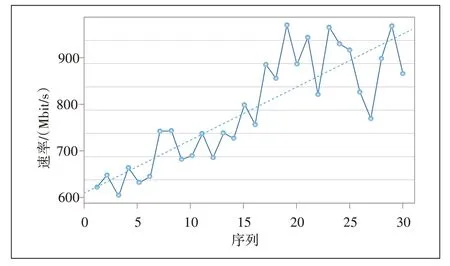
图2 线性拟合模型

该线性拟合模型可以表示为：

依据式（1），可以计算出未来3期线性拟合模型的预测值，如表1所示。

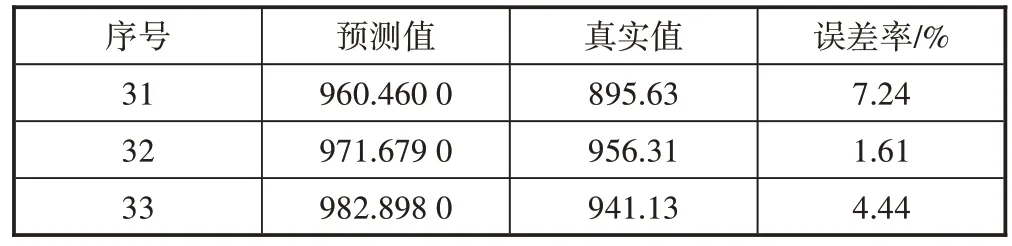
表1 线性拟合模型的3期预测值与误差率

2.2 平滑法

平滑法通过对过去数据的加权平均处理，减少短期波动对序列的影响，尽可能地展示数据的直观趋势。

移动平均法是最常见的数据统计分析方法之一，通过计算过去n期数据的平均值作为预测值，其表达式为：

图3所示为4期平均移动法的流量拟合。

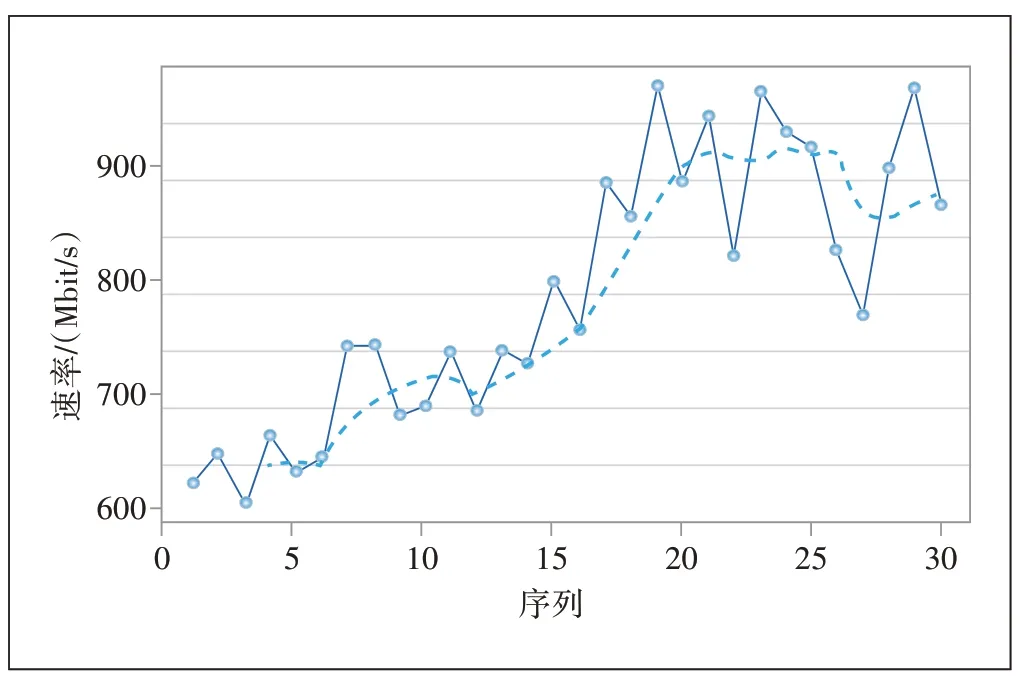
图3 移动平均拟合模型

依据式（2），可以计算出未来3期移动平均模型的流量预测值和预测误差率，如表2所示。

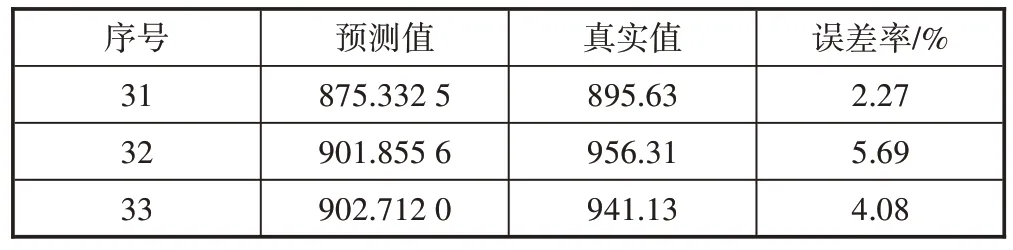
表2 移动平均模型的3期预测值与误差率

移动平均法简单直观，以前n期数据的平均值作为最后一期的预测值，往期数据的权重都是1/n，即在移动平均法中，n期的每一条数据对预测值的影响是相同的。但在实际流量分析中，不同时间的数据对当前流量大小的影响是不同的（一般时间越近，影响越大），为了更好地反映这种情况，需要调整往期数据的权重。美国统计学家Holt 在简单指数平滑法的基础上，添加了对长期趋势拟合，提出了Holt 两参数指数平滑模型，该模型适用于含有递增趋势的序列，Holt两参数指数平滑模型的平滑公式为：

式中：

θt——序列每阶递增量

α，β——2个平滑系数

该模型后经Winters 改进，形成了Holt−Winters 三参数指数平滑模型，该模型除了可以拟合长期趋势，还可以拟合周期性变化。

考虑到图1 流量时序图中仅包含递增趋势，为其建立Holt 两参数指数平滑模型并进行3 期数据预测，结果如图4所示。

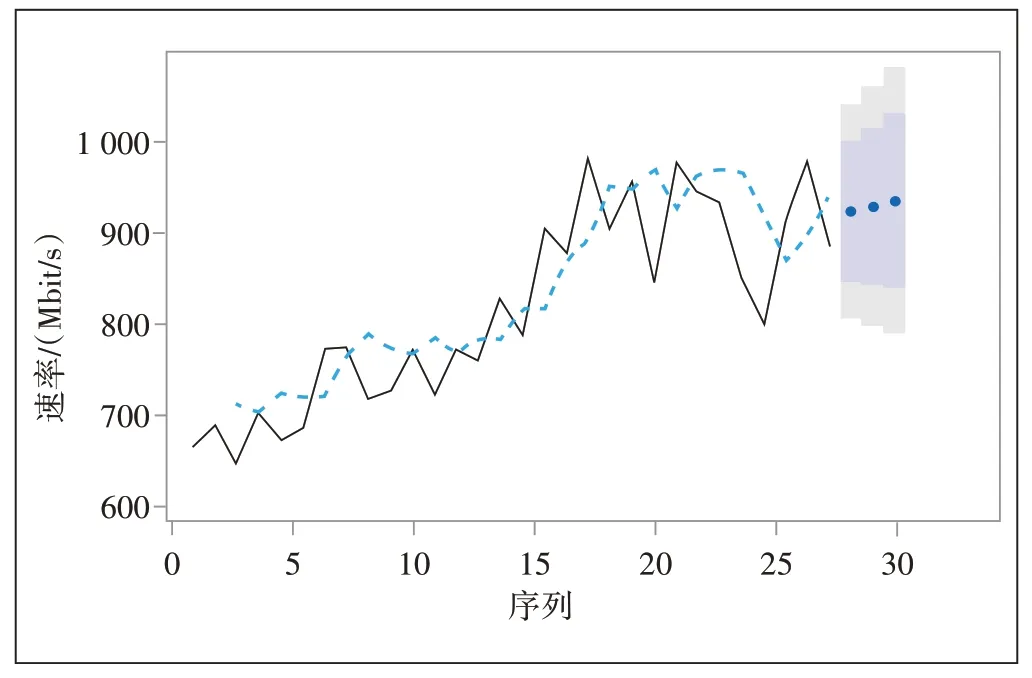
图4 Holt两参数指数平滑拟合模型

图4 中黑色实线是流量观测值，蓝色虚线是模型拟合值，蓝色点为预测值，浅色阴影为95%的预测值置信区间，深色阴影为80%的预测值置信区间。预测值和预测误差率如表3所示。

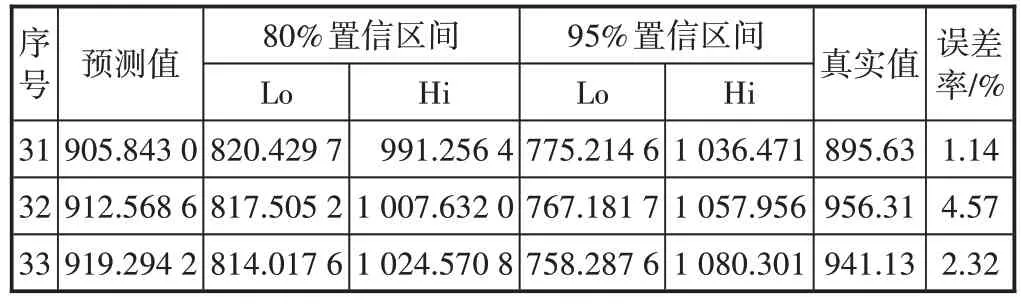
表3 Holt两参数指数平滑模型的3期预测值和预测误差率

2.3 ARIMA模型

ARIMA（Autoregressive Integrated Moving Average Model）模型全称为差分自回归移动平均模型，由美国统计学家Box 和英国统计学家Jenkins 提出［11］，是在ARMA模型的基础上增加了差分运算的时间序列分析模型。ARMA模型对平稳序列的分析技术已经非常成熟，如果一个序列可以通过差分使之变为平稳，那么使用ARIMA 模型对该序列的分析也将是可靠、易行的［12−15］。ARMA 模型是AR 模型和MA 模型的有机组合，具有如下结构的模型称为ARMA（p，q）模型：

式中：

φp、θq——AR部分和MA部分的待估参数

εt——零均值、方差记为的白噪声

如果一个序列{X(t),t∈T}可以通过d次差分得到一个平稳的过程，且该过程服从ARMA（p，q）模型，则称{X(t),t∈T}是ARIMA（p，d，q）过程［16］。

图1 的流量时序图中有明显的递增趋势，且ACF图中自相关系数衰减较慢，在16阶延迟附近又落在了2 倍标准差的参考线之外，显著不为0，因此可以认为该流量数据为非平稳时间序列。考虑到时序图中的递增趋势，尝试使用差分运算将其转化为平稳时间序列。

对流量数据进行一阶差分运算，做出其时序图、自相关系数图、偏自相关系数图（见图5）。

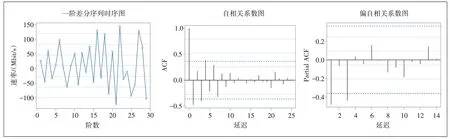
图5 一阶差分序列的时序图和相关性分析图

从图5可以看出，该差分数列时序图的均值稳定、波动范围有限且无明显趋势或周期，自相关系数迅速衰减到0 附近，该差分序列可能为平稳时间序列。进一步使用ADF 检验对该序列的平稳性进行统计检验，检验结果如表4所示。

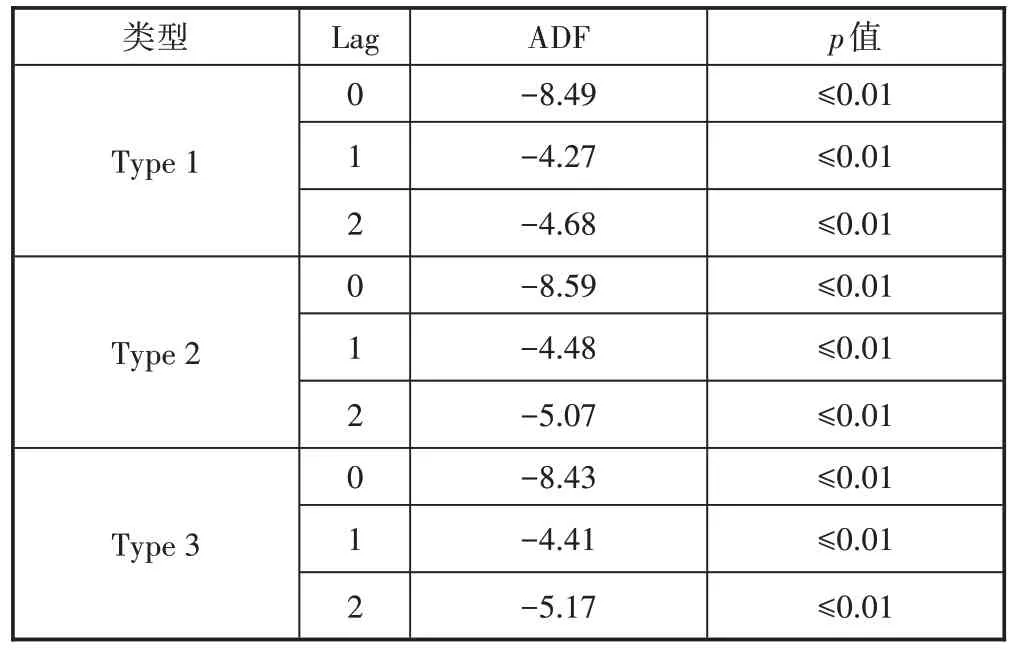
表4 一阶差分序列的ADF检验

从表4可以看出，3种类型的p值均明显小于0.05，因此拒绝原假设，该序列为平稳时间序列。

在平稳时间序列中，若某一时刻的状态对下一时刻没有相关性，则意味着该序列未来的数据无法通过现在及过去的状态进行推断，对这样的流量数据进行预测是没有价值的。因此要进行纯随机性检验，判断该流量数据是否有预测价值。

在图5 中，一阶差分序列的ACF 图中，1、3、4 阶自相关系数明显不为零，初步判断该序列不是纯随机序列，进一步考察该序列的LB统计量，结果如表5所示。

表5 一阶差分序列的纯随机性检验

从表5 可以看出，一阶差分序列延迟6 阶、12 阶的LB统计量的p值均明显小于0.05，所以拒绝原假设，该一阶差分序列不是纯随机序列，可以用来做预测分析。

通过上面的分析可知，原流量数据经过一阶差分运算后是一个平稳的非纯随机性序列，这样就可以为差分序列构建ARMA 模型。在图5的ACF图中可以看出一阶差分序列的自相关系数呈现逐渐衰减的趋势，符合拖尾特征；PACF 图中，只有一阶和三阶偏自相关系数落在了2 倍标准差范围外，剩下的系数趋向于0，可认为是一阶、三阶截尾或拖尾。尝试选择MA（1）、MA（3）、ARMA（1，1）、ARMA（4，1）模型拟合该差分序列。模型的选取应遵从从简原则，在能充分表示序列的前提下所含参数个数应该最少［16］，因此对4 个ARMA 模型进行最小信息量检测，检测结果如表6 所示。

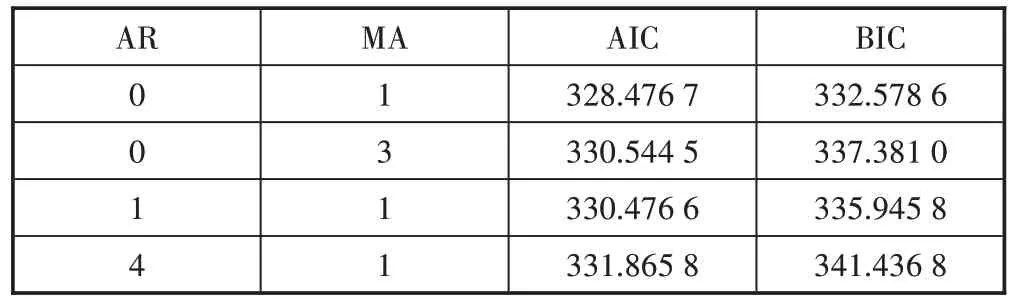
表6 ARMA模型参数评估

从表6 可以看出，无论是AIC 还是BIC，MA（1）模型都是最优选择，结合该序列为流量数据通过一阶差分得到，因此使用带漂移项的ARIMA（0，1，1）模型来拟合原流量数据。为考察ARIMA（0，1，1）的有效性，对其进行显著性检验，即对残差序列的检验，结果如图6所示。

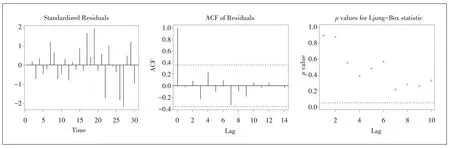
图6 残差序的标准化残差图、ACF和纯随机性检验图

从图6 可以看出，残差序列的各阶白噪声检验统计量的p值均大于0.05，原假设成立，残差序列是白噪声，即该拟合模型显著成立，因此为流量数据建立ARIMA（0，1，1）模型，并进行3 期流量预测，图7 为拟合模型的预测效果，表7列出了预测值和预测误差率。

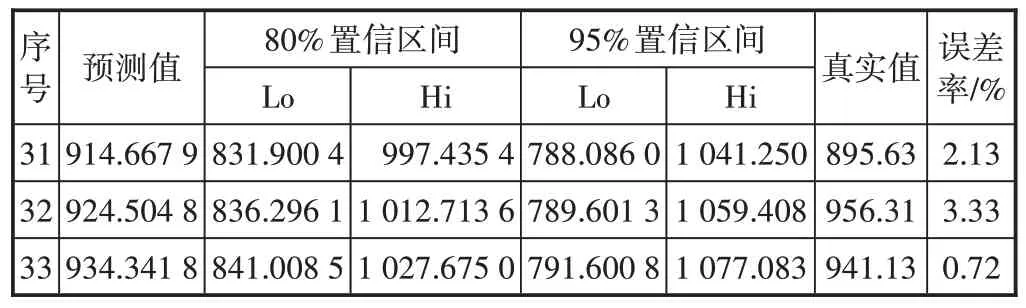
表7 ARIMA（0，1，1）模型的3期预测值、置信区间与误差率

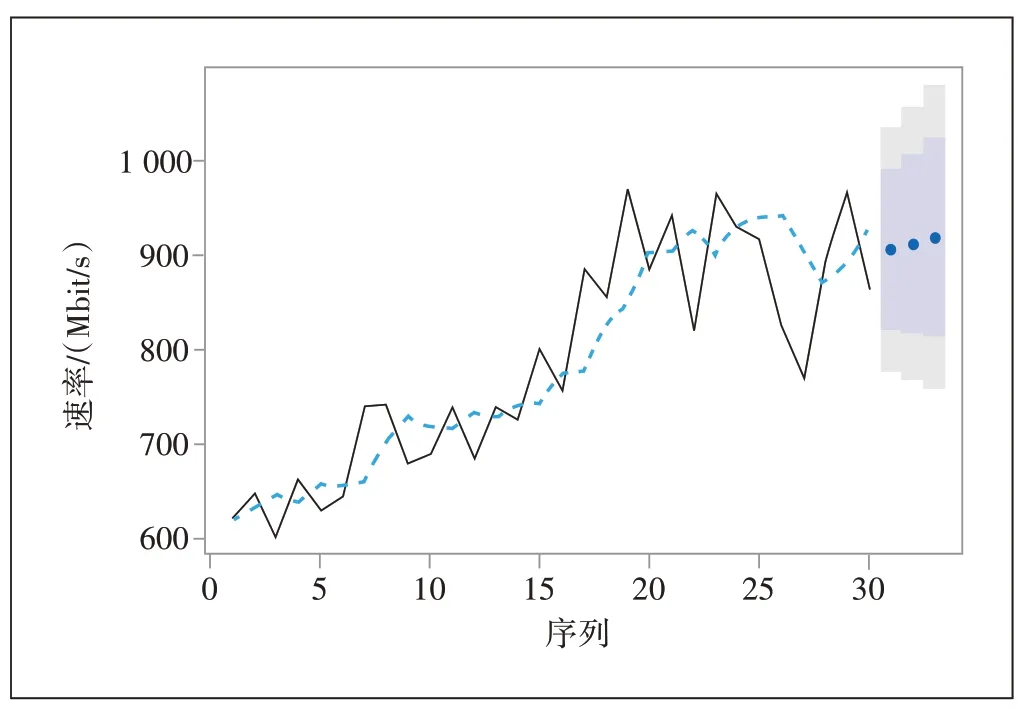
图7 ARIMA（0，1，1）拟合模型的预测效果

图7 中黑色实线是流量观测值，蓝色虚线是模型拟合值，蓝色点为预测值，浅色阴影为95%的预测值置信区间，深色阴影为80%的预测值置信区间。

2.4 模型预测结果比较

文章针对OLT 流量构建了线性拟合、平均移动、Holt两参数指数平滑和ARIMA（0，1，1）4 种模型，为评估各模型的预测性能，采用平均绝对百分比误差（MAPE）作为评价指标，4种模型的平均绝对百分误差（MAPE）如表8 所示。从表8 可以看出，ARIMA（0，1，1）和Holt 两参数指数平滑模型的预测平均误差率为2.06%、2.68%，误差相对都比较小，预测效果表现较好；而线性拟合和平均移动模型的预测误差分别为4.43%、4.01%，误差较大，不适合用来对精度有较高要求的流量进行预测。

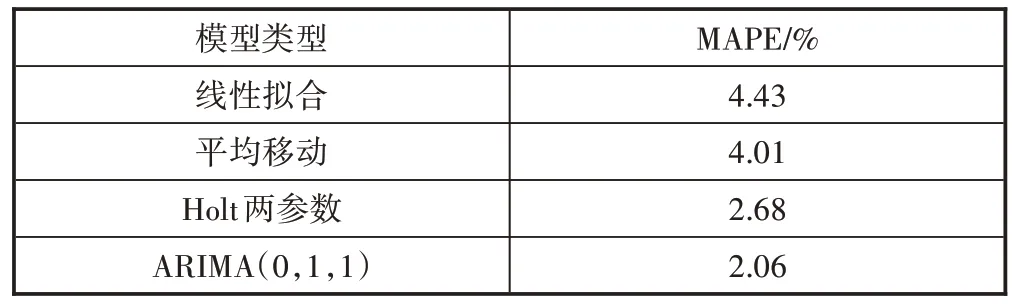
表8 4种模型的平均绝对百分误差（MAPE）

3 预测评价

网络流量信息具有很大的随机性，前一日的流量大小理论上不能影响到当日的流量，对流量预测的本质是对用户上网习惯的推断，个人行为具有很大的随机性，群体行为表现出的规律性更大，因此越是靠近北向的端口，对流量进行的统计学分析的意义越大，这也是文章对OLT 上联口分析的原因。对应地，越是南向的设备，流量表现出的随机性越强，此时筛选出有意义的数据比逐个预测更有价值。

本文使用到趋势拟合法和平滑法对流量数据进行建模预测，这些方法具有原理简单、操作简便、易于解释等优点，在提取明显的、确定的信息时有一定优势，缺点是相关性信息在加权平均中丢失，随机性信息浪费严重，这可能是本文在流量预测时ARIMA 模型略优于Holt模型的原因，使用ARIMA 模型在处理平稳序列、差分平稳序列时可以更加充分地体现流量中的短期相关关系。

4 展望

本文以周数据进行数据建模与网络流量预测，预测获得了不错的效果。伴随着运营商算力的提升，未来若能够拿到海量的流量数据，则可以考虑使用LSTM 等机器学习来拟合更加复杂的模型。但并不是所有预测问题都适合使用机器学习，在多变量的非线性时间序列预测时，特别是在大样本的情况下机器学习会获得更好的表现，针对平稳或差分平稳时间序列，在样本较少的情况下，使用ARIMA 等统计建模法更具优势［17−20］。

流量数据会受到多种因素影响，在后续的研究中应该考虑将现有模型与其他预测模型进行组合，构建多因素的组合模型，以缓解模型预测的滞后问题，提高预测灵敏度和准确性［21−24］。