矢量圆法在高中物理解题中的应用
刘宏松
(广西柳州铁一中学)
科学思维作为物理学科四大核心素养之一,主要包括模型构建、科学推理、科学论证、质疑创新等要素。新课标要求学生基于观察和实验,建构物理模型,应用数学等工具,通过科学推理和论证,形成系统的研究方法和理论体系。因为受到应试教育的影响,部分教师在讲授习题课时重视讲授题目答案,轻视物理规律的形成过程,不利于学生形成良好的科学思维习惯,为了解决这一问题,本文通过介绍矢量圆法的应用,帮助学生养成注重物理规律形成过程的思维方式,促进学生核心素养的提高。
圆作为一个数学工具在中学物理涉及的较多,巧妙地应用圆,有利于把抽象的过程直观化。若物理矢量是变化的,且其矢端始终落在一个圆周上,作出这个圆,便是矢量圆。利用矢量圆法解决一些高中物理问题时,可以直观地显示各个物理量的变化过程,帮助学生拨开层层迷雾,加深对物理规律的理解,启迪学生的思维,有助于物理学科科学思维的形成和发展。下面介绍矢量圆法在高中物理的一些应用。
一、矢量圆在力学平衡问题中的应用——求合力和一个分力的夹角范围
对于大小恒定、方向不定的矢量,为了能够形象地描述它,我们以矢量长度为半径作一圆,则从圆心向圆上任一点的有向线段代表矢量的一种可能值。
【例1】已知合力F=10 N,它的一个分力F2=8 N,求另一个分力F1与F的夹角取值范围?
【分析】如图1所示,作出合力F的力的图示,以F的矢量箭头为圆心,以力F2的大小为半径画圆。从O点向圆上一点引一条有向线段,即为分力F1的一个可能值。由图结合数学知识可知,F1与F的夹角的最大值出现在F1与圆相切时,分力F1与F的夹角最大值满足sinθ=0.8,夹角最小值为零。
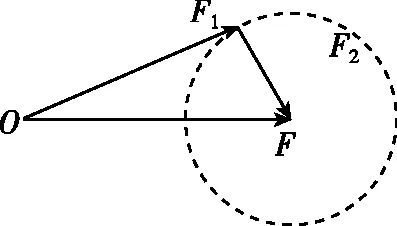
图1
二、矢量圆在运动的合成与分解中的应用——小船以最短位移渡河
【例2】某人划船,船在静水中的速度v1=3 m/s,若船在流速为v2=5 m/s的河中行驶,要使船渡河的路径最短,则他应该怎样控制船的航向?
【分析】理论上最短渡河路径垂直河岸,但是因为船的静水速度小于水流速度,导致无论船的航向如何,都不可能垂直河岸渡河。考虑到船的静水速度大小恒定,方向不定,可以引入矢量圆。
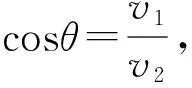
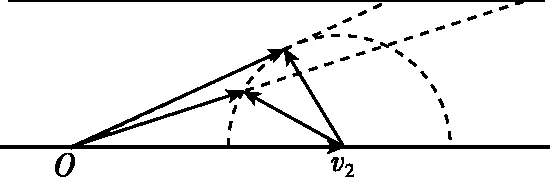
图2
三、矢量圆在匀速圆周运动中的应用
1.竖直面内的匀速圆周运动
【例3】如图3,一轻杆一端固连一小球,在竖直面内绕O点做匀速圆周运动。在小球运动一周过程中,轻杆的弹力怎么变化?
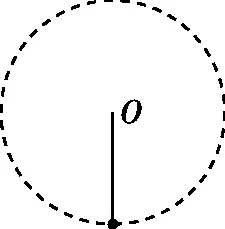
图3
【分析】对小球受力分析如图4,小球的向心力mω2r大小恒定,方向时刻指向圆心,重力mg不变。小球的向心力mω2r的矢量将做匀速圆周运动。向心力mω2r的矢量起点形成一个圆,从圆上一点向重力矢量起点引一条有向线段即为杆的弹力F。由图4可知,随着向心力矢量方向绕圆心旋转,小球通过最高点时,力F的最小值为Fmin=mg-mω2r;小球通过最低点时,力F的最大值为Fmax=mg+mω2r。
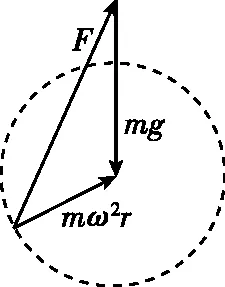
图4
2.倾斜面内的匀速圆周运动
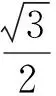
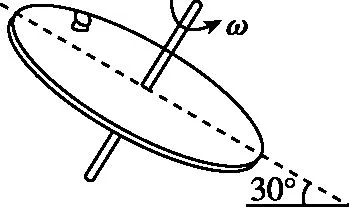
图5
【分析】在很多参考答案中,都是直接给出结论,即物体在最高点时静摩擦力最小,最低点时静摩擦力最大,至于原因是什么,都避而不谈。这样的处理方式很不利于学生科学思维的形成,容易引起学生的困惑。本题若采用矢量圆来处理,可以形象直观地看到不同位置摩擦力的变化情况。方法如下:以物体的向心力mω2r的矢量长为半径作一圆,重力沿斜面的分力mgsinθ的矢量方向始终竖直向下,长度一定。
从圆上一点向mgsinθ的矢量图的起点引一条有向线段,即为静摩擦力f。mgsinθ与mω2r的大小关系不知道,需要分三种情况讨论:
mgsinθ>mω2r mg sinθ=mω2r
由图6、图7、图8可知,在最高点时静摩擦力最小,最低点时静摩擦力最大,三种情况的结论一致。故只要保证最低点物体与圆盘不相对滑动,即可保证在其他地方都不相对滑动。
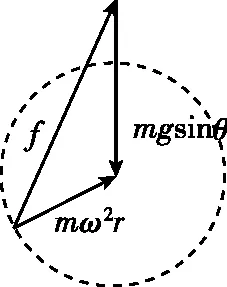
图6
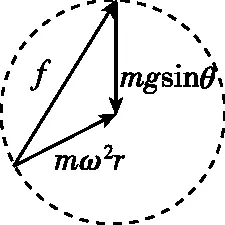
图7
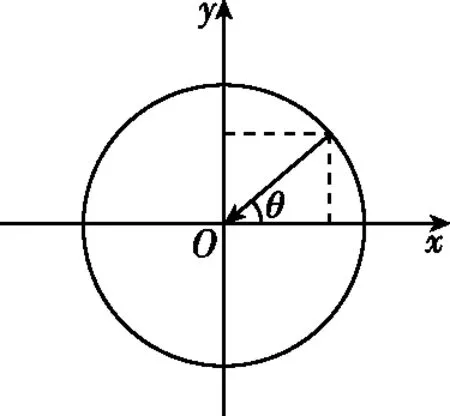
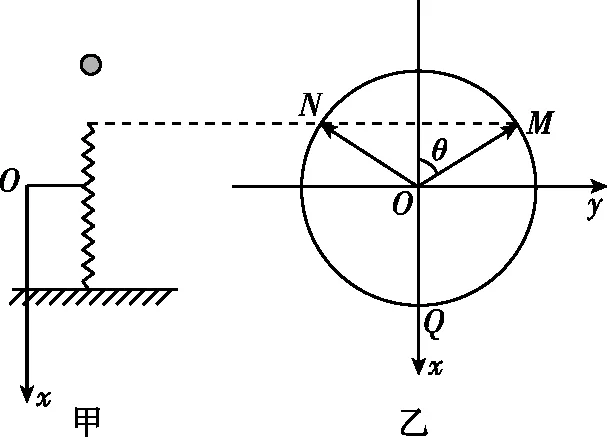
mgsinθ 图8 针对此题,若最低点物体与圆盘恰不相对滑动,则有 f=μmgcosθ① f-mgsinθ=mω2r② 联立①②解得ω=1 rad/s,此值即为ω的最大值。 矢量圆法的理论分析:如图9所示,一质点沿一半径为A的圆周以角速度ω沿逆时针方向做匀速圆周运动,t=0时刻,质点在x轴正半轴上。在任意t时刻,质点做匀速圆周运动的向心力F=mω2r,经时间t,质点转过的角度为θ。向心力水平分量为 Fx=mω2rcosθ③ 竖直分量为Fy=mω2rsinθ④ 质点的坐标:x=rcosθ,y=rsinθ⑤ 联立③④⑤得Fx=mω2x,Fy=mω2y 以圆心为原点,建立如图9所示坐标系。考虑Fx与x的方向关系 图9 Fx=-mω2x,Fy=-mω2y 令k=mω2,则Fx=-kx,Fy=-ky 匀速圆周运动的水平分力和竖直分力都是符合简谐运动的回复力表达式。即证明了匀速圆周运动的水平分运动和竖直分运动都是简谐运动。利用合运动与分运动的等时性,可以将简谐运动的求解时间的问题转化为匀速圆周运动求解时间的问题。下面举例说明: 【例5】如图10甲所示,一个劲度系数为k的轻弹簧竖直固定在桌上,现将一质量为m的小球在距离弹簧上端h处由静止释放,小球压缩弹簧距离d后返回至释放点,求该过程的时间? 图10 【分析】以小球的平衡位置为原点,竖直向下为x轴正方向,建立一维坐标轴,小球的平衡位置处弹簧的压缩量记为x,则 mg=kx⑥ 小球自由落体阶段的末速度记作v,时间为t1,则 v2=2gh⑦ 简谐运动的振幅为 由⑥式,对于小球刚接触弹簧的时刻,小球相对平衡位置的位移为 由此可得简谐运动的振幅 如图10乙,为了求解简谐运动的时间,以A为半径作一矢量圆,小球与弹簧相互作用的时间等于匀速圆周运动的质点从M经Q到N的时间,即 小球离开弹簧后返回至最高点的时间为t3 t3=t1 科学思维是物理核心素养的重要内容之一,在高中习题课的教学中,要帮助学生去挖掘问题的物理本质,寻找其科学规律,改善学生的科学思维能力,尽量避免被动地接受、记忆式的学习方式。这对于学生科学思维的培养将大有裨益,也容易激发学生科学探究的欲望,培养学生的科学态度与责任。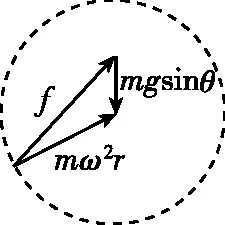
四、矢量圆在简谐运动中的应用
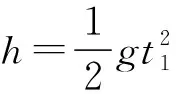
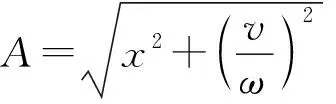

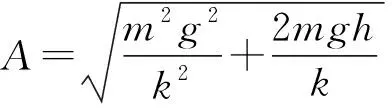
五、结语

